缺资料城市洪灾损失率函数构建方法及应用

吕 鸿,吴泽宁,管新建,王慧亮,孟 钰,江鹏昆

(郑州大学水利科学与工程学院,河南 郑州 450001)

在全球极端气候频发和高速城市化双重因素主导下,城市洪涝灾害发生的频率和强度正急剧增加,严重威胁城市安全[1]。量化与评估城市受淹区域的损失,不仅可以及时采取减轻灾害的针对性措施,还可对灾后的恢复和重建提供参考依据[2]。对于自然灾害保险业来说,精确的洪水损失评估结果对灾后理赔不可或缺[3]。因此,科学、合理、高效地量化洪灾损失,对实施城市洪灾风险管理和应急决策具有重要意义。洪灾损失评估受区域降雨特征、地理条件、社会经济水平等多重要素的影响,具有多维性、复杂性和多学科交叉的特点,评估手段形式多样[4-5]。利用损失率函数结合洪水淹没深度、土地类型和经济要素形成损失结果,是国际上广泛采用的洪灾损失评估方法[6]。很多城市因缺乏洪灾灾情资料,使得这种评估方法实施困难,提出普适的缺资料城市洪灾损失率函数构建方法,对量化缺资料城市洪灾损失十分必要。

以洪灾淹没水深为自变量、社会经济价值损失率为因变量,是国内外构建洪灾损失率函数的主要形式。利用区域的历史洪灾统计资料,采用相关分析、回归函数、神经网络等,建立不同淹没水深和洪灾损失率的函数关系[2,4,6-7]，这类研究方法对基础数据资料的要求较高,很多城市缺乏甚至没有历史灾情资料[8],难以满足直接构建洪灾损失率函数要求。针对灾情资料较缺乏的情况,部分研究者做了一些损失率数据移植尝试,主要分为直接移植[9-10]和间接移植[8,11-12]。直接移植是将引用区洪灾损失率数据直接应用到研究区；间接移植是选取能够代表区域洪灾影响的指标,通过比拟原理,将离散的引用区损失率数据间接移植到研究区。由于区域间致灾、承灾和防灾等要素差异,引用区的损失率存在区域局限性,直接移植到其他区域准确性较差[10]；间接移植采用单一转换因子(引用对象和比拟指标)存在偶然性和主观性等不确定性。此外,移植后引用区数据多以二维表格或者离散数据展示,缺乏连续型函数拟合[8],或者采用单一拟合函数形式也存在偶然性和主观性等不确定性。若将对象、指标、函数的维度增加,则需要解决不确定性与最优性问题[8]。

本文以洪灾灾情资料缺乏的郑州市为例,针对损失率数据移植中的不确定性,以比拟原理为基础,考虑多引用对象和多特征指标,将比拟因子扩充后形成损失率移植矩阵,通过建立多函数拟合情景,优化构建缺灾情资料城市洪灾损失率函数,以期为缺资料城市或地区的洪灾损失提供一种评估方法。

1 缺资料城市洪涝灾害损失率函数的构建方法

1.1 移植原理和建模思路

水文比拟法借鉴传统代数学中等比例替代思想,常用来解决很多水文学中的缺资料或无资料问题[8]。本研究的基本思路如式(1)所示,利用已知灾情资料的引用城市损失率(R0)、影响洪灾损失的比拟指标I(研究区)和I0(引用城市),推求研究区损失率(R)。即通过双向比拟因子扩充,基于比拟原理变换为移植矩阵；利用“损失率移植矩阵变差系数最小、概率最大和相关系数最大”3个目标准则,驱动多拟合情景,构建研究区洪灾损失率函数。形成一种“因子变异-动态比拟-目标驱动-情景拟合”的缺资料城市洪灾损失率函数构建方法。

(1)

式中:λ为移植系数。

1.2 双向扩充构建变异比拟因子

(1)变异引用对象。考虑多引用对象,通过数据挖掘得到多个有资料城市的损失率数据,若m个引用城市存在损失率数据R0m(i=1,2,…,m),可组成引用损失率矩阵R0,即

(2)

(2)变异比拟指标。考虑多特征指标,分析影响损失率的城市经济水平、承灾和防灾等要素,选取K个代表性特征指标,建立特征指标体系I=(I1,I2,…,IK)。利用随机组合方案替代单一性比拟指标,将K个特征指标随机组合形成n种特征组合方案(式(3))。比拟因子是单一数值,利用投影寻踪模型将特征组合方案转化为特征综合值[8]。令Zj表示研究区第j个方案下的特征综合值,j=1,2,…,n；令Z0ij表示第i个引用区第j个方案下的特征综合值,i=1,2,…,m。

(3)

1.3 基于动态比拟的缺灾情资料城市洪灾样本移植

(1)移植系数矩阵。依据式(1),设λij为第i个引用城市的第j个方案的移植系数,令λij=Zj/Z0ij,可得到m×n种组合方案的移植系数矩阵A:

(4)

(2)损失率移植矩阵。联合式(2)和(4),通过式(1)可转变为m×n阶的研究区损失率移植矩阵R(式6)。但它仅仅是某一淹没水深下的移植矩阵。

(5)

步骤一:每个特征方案下的损失率集对应着矩阵R的列向量,并计算每1个列向量的变差系数CVj,构成变差系数集CV。

(6)

式中:uj为第j组列向量的平均值；σj为第j组列向量的方差。

(7)

(8)

1.4 基于Beta分布概率最大目标确定函数拟合序列

为降低引用数据的统计不确性,采取构建Beta分布提取概率最大值R′作为某一淹没水深的采用损失率。选择Beta分布的原因:① 自变量x取值范围为[0,1],契合洪灾损失率函数的定义域；② Beta分布契合损失率分布“中间多两边少“的统计学特征；③ 已有部分研究[8,12-13]采用多样本数据拟合损失率的Beta分布。

Beta分布的概率密度函数如下:

(9)

(10)

式中:α和β是Beta分布的参数,α>0且β>0。

(11)

(12)

式中:μ与σ为样本均值与方差。

(13)

式中:P是第h级水深下损失率的Beta分布的所有可能概率。

(3)确定函数拟合序列。依次重复H次前述步骤,即可得到一种财产类型H个最优损失率值组成的待拟合序列FS,如下:

(14)

1.5 多拟合情景优化构建洪灾损失率函数

目前洪灾损失率函数尚未形成统一形式,表1展示了目前国内外研究中出现的多种函数形式。如将洪灾损失特征概化为初期较慢、中期迅急、后期再趋缓状态的3种S型增长函数；国外研究者使用较多的线性-指数型函数,拟合稳定且能简略概化损失机制；初期无先验知识的研究者普遍使用的多项式拟合。将这些函数形式作为本研究待拟合函数集。

表1 目前研究中存在的洪灾损失率函数Table 1 Water depth-loss rate function in current research

(1)设置不同拟合情景。与单一比拟因子的不确定性问题相似,如果简单地选择某一个函数形式也存在主观性和偶然性。本研究在函数集的基础上,设置3种拟合情景:简单独立型、分段随机型和组合随机型,通过相关系数最大原则来改善单一函数的不确定性问题及提升序列拟合的契合度。

情景1:简单独立型拟合 简单独立型拟合是最为普遍的函数拟合方法,将函数拟合序列FS分别拟合F1—F6,即情景1存在6种拟合形式。此情景原理简单便捷,但缺点突出,如单一函数往往会出现局部拟合较好整体较差的情况,无法充分利用多维函数组合的高维组合特征优势。

情景2:分段随机型拟合 由于单一函数的固定曲线图像,使其拟合时存在“中间拟合好两边拟合差”的现象,本研究提出了“分段随机型拟合”情景,即依据函数拟合序列FS的聚类性质自动寻找其间断点,然后进行分区间拟合(式(15)),以提高整体拟合效果。实施步骤为:先依据轮廓系数法确定最优分段数目(d),即分段中心与同簇类距离尽可能近,异簇类距离尽可能远；再基于分段数目,采用K-means聚类算法,进行拟合序列的区间划分；最后在每一区间上进行简单独立型拟合。情景2具有了6d种拟合形式。

(15)

式中:S0～Sd是水深区间起始值；Fx是函数集F1—F6的随机选择。

(16)

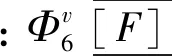
(2)设置相关系数最大原则。3种情景共有6+6d+57种拟合形式,依据相关系数(CC),最大原则遴选出最优的函数形式(式17),即构建了土地类型的水深-损失率函数。

F*=max{CC|CC(FS,ytr),t∈[1,3]r∈[1,R]}

(17)

式中:r表示第t种情景下的拟合形式数；ytr表示第t种情景下的第r种拟合形式。

2 实例应用与分析

2.1 研究区概况及数据处理

2.1.1 研究区概况

河南省郑州市,地处华北平原南部,国家中心城市,2019年常住人口超过1 000万。受温带季风气候和城市化水文效应的影响,65%以上的降雨量集中于汛期(7—9月),且排水设施不完善,城市极易遭受内涝。洪灾频率高、空间分布数量多,但受灾强度不大、量级小,缺乏洪灾损失的系统调查与资料存储[17]。随着极端气候激增和城市化的高速发展,城市洪灾风险增高,经济损失已经不容忽视。迫切需要提出洪灾损失的量化评估方法,为城市洪灾灾害风险管理提供支撑。

2.1.2 数据挖掘和处理

(1)数据挖掘建立引用数据库。以中国所有城市为对象,利用数据挖掘技术,挖掘得到11个引用城市的灾情数据:上海[11]、深圳[12]、温州[15]、天津[18]、西安[19]、濮阳[20]、沈阳[21]、广州[22]、无锡[23]、哈尔滨[24]、珠海[25]等城市,将被研究的水深离散为40级(0.1～4.0 m,即H=40),建立引用城市的损失率数据库。

(2)建立特征指标体系。按照变异比拟指标构建方法,考虑郑州及各个引用城市的指标数据获取性,选取5个代表性指标建立特征指标体系(表2),即K=5,n=31。

表2 影响洪灾损失率的特征指标体系Table 2 Characteristic indicator system affecting flood loss ratio

(3)城市土地类型划分。为体现城市土地利用的复杂特征以及挖掘数据的分类特征,采用多源数据融合及人工目视解译辅助,将城市土地类型划为4种,分别为工业、商业、住宅和公共服务,最终得到这4种土地类型的损失率函数。

2.2 动态比拟过程分析

2.3 Beta分布概率最大值分析

图2 4种土地类型的40级水深的最大概率损失率值R′和拟合序列FSFig.2 Maximum probability loss rate R′ value and the fitted sequence FS of the 40-level water depth of the 4 land types

2.4 不同拟合情景对比

图3 3种拟合情景下的拟合相关系数展示Fig.3 Fitting correlation coefficients under 3 fitting scenarios of the 4 land types

图4 3种拟合情景下的平均相关系数对比Fig.4 Comparison chart of average correlation coefficients under 3 fitting scenarios of the 4 land types

2.5 损失率函数结果

图5 4种土地类型的洪灾损失率函数Fig.5 Flood loss rate function diagram of 4 land types

3 结 论

围绕缺灾情资料城市洪灾损失率函数构建问题,本文考虑多引用对象、多特征指标、多拟合情景的多维度优化,提出“因子变异-动态比拟-目标驱动-情景拟合”的建模框架,克服缺资料城市灾情数据局限性,主要结论如下:

(1)借鉴等比例替代的数学思想,通过提出洪灾损失率函数参数化的构建模式,实现以多引用城市灾情资料为数据源、缺资料城市的特征指标为参数输入、损失率函数为输出的方法体系,为缺灾情资料城市或地区提供技术参考。

(2)在基于比拟指标的灾情数据间接移植过程中,不同土地类型和不同水深对应的特征指标都存在差异化现象,表明单一比拟指标会忽视不同城市间和城市内不同承灾体洪灾损失影响要素的差异,存在指标选取的偶然性和主观性等不确定性。

(3)用多种函数的随机线性组合拟合洪灾淹没水深-损失率数据,能显著提高拟合的相关性,降低单一函数选择和主观性影响,可改善分段函数拟合的阶段点不连续问题,为样本-函数拟合研究提供了新思路。