基于广度优先的最小独立闭合环搜索及其实现

夏先勤

（安徽理工大学空间信息与测绘工程学院，安徽 淮南 232001）

水准网路线环闭合差自动检核的第一步是找到最小独立闭合环[1]。实现最小独立闭合环自动搜索的主要思想可以归纳为4类：基于生成树和余树的思想[2]、基于深度优先的思想[3]、基于广度优先的思想[4]、基于邻接矩阵变换的思想[5]。本文详细阐述了基于广度优先的最小独立闭合环搜索算法，并在此基础上采用Python（计算机编程语言）实现了水准网最小独立闭合环搜索及其闭合差检核的程序设计。

1 基于广度优先的最小独立闭合环搜索

基于广度优先的最小独立闭合环搜索在更新邻接点集合时将记录所有的邻接点，而不会判断邻接点是否被访问过[6]。以从无向图G中搜索以顶点v1，v2，v3组成的最小独立闭合环为例（见图1），本文基于广度优先搜索的思想来实现最小独立闭合环搜索的主要过程描述如下。

图1 无向图G

步骤一：在图中选择起始顶点v1，搜索层次k=1，搜索得到k=1层根节点v1的所有邻接点组成的集合为

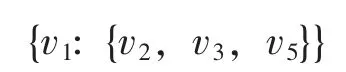
步骤二：搜索层次k=2，搜索得到k=2层根节点v2，v3，v5的邻接点并将邻接点集合更新为

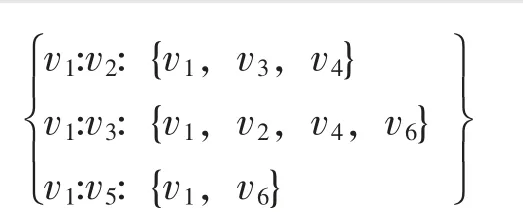
在每个子集中删除k=1层根节点，得到邻接点集合为

步骤三：搜索层次k=3，以步骤二中搜索到的3个邻接点子集为基础，搜索得到k=3层根节点v2，v3，v4，v6的邻接点并将邻接点集合更新为

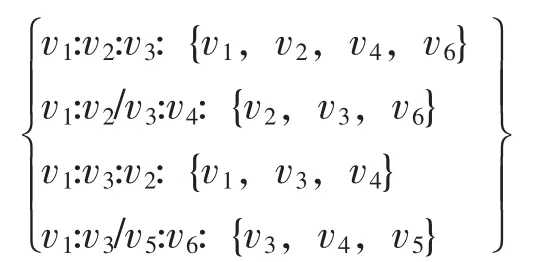
其中v2/v3表示v2或v3，v3/v5同理。

步骤四：此时n≥3，判断是否形成最小独立闭合环：步骤三所得到的集合的子集中，集合v1:v2:v3:{v1，v2，v4，v6}与集合v1:v3:v2:{v1，v3，v4}都包含有k=1层根节点v1；提取各层根节点组成集合{v1，v2，v3}，此时认为搜索到了最小独立闭合环，最小独立闭合环的顶点即为v1，v2，v3。

2 基于Python的程序设计

2.1 水准网数据的组织

将原始水准网数据存储在“.txt”文件中，已知点数据以“#”开头作为标记；示例中已知点为F，其高程为11.414 m。已知点数据之后为测段数据，以第一个测段为例， “A”为测段后视点， “B”为测段前视点， “73.795”为测段高差（单位：m），“20.400”为测段长度（单位：m）。水准网数据格式示例如下。

采用Python内置的 “.readlines()”函数将文本文件读取到列表中，然后对列表中的每一行采用“.strip()”函数截取掉所有的回车字符，进而采用“.split(‘ ’)”将得到的整行数据分割成元素列表。最终读取到程序中的水准网数据以二维列表的形式存储，二维列表中的子列表按顺序对应着文本文件中的某一行。以水准网数据格式示例中的前三行数据为例，程序读取后会将其存储为二维列表：[[‘F’，11.414]，[‘A’， ‘B’，73.795，20.400]，[‘A’， ‘D’，14.005，18.800]]。

2.2 程序算法

程序实现的基本框架是基于广度优先的最小独立闭合环搜索算法，但如果在程序实现过程中仅采用基于广度优先的最小独立闭合环搜索的话，在某些特殊情况下会遗漏最小独立闭合环[7]。以无向图G′的最小独立闭合环搜索为例（见图2），采用基于广度优先的最小独立闭合环搜索算法进行搜索时，无论是以{v1，v2，v3，v4，v5，v6，v7，v8}哪一个结点作为搜索的起始顶点，都只能搜索到{{v1，v5，v6},{v2，v6，v7},{v3，v7，v8},{v4，v5，v8}}这4个最小独立闭合环中的一个，而中间四顶点的最小独立闭合环{v5，v6，v7，v8}将被遗漏[8]。

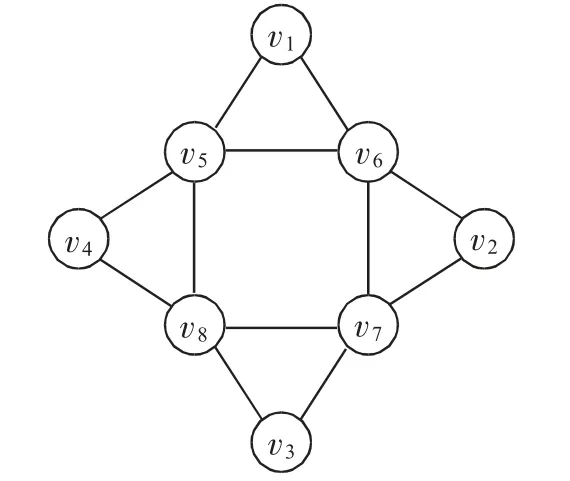
图2 无向图G'

为此，本文在具体程序实现时在基于广度优先的最小独立闭合环搜索算法中嵌入“深度搜索”的过程[9]，这一过程仅在当前搜索到的最小独立闭合环已经存在的情况下执行。进行“深度搜索”的具体流程见图3。

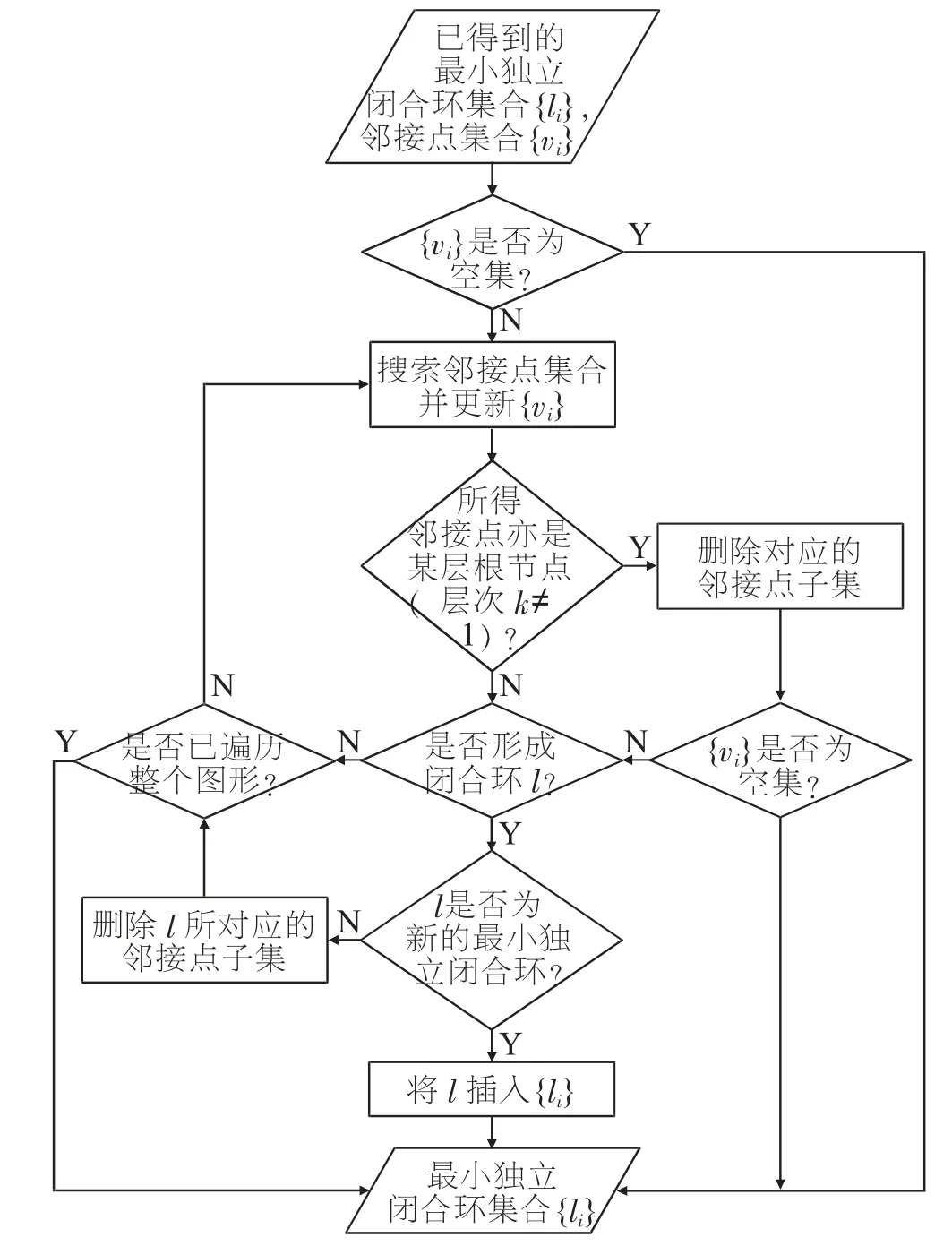
图3 深度搜索流程图

3 实例验证

为验证本文中所设计的算法的正确性与有效性，选取某次工程应用中的二等水准网实例数据对其进行测试[10]。所选取的水准网共有21个水准点，37个测段，其中BM1，BM2，BM3，BM4与BM5为已知点，见图4。

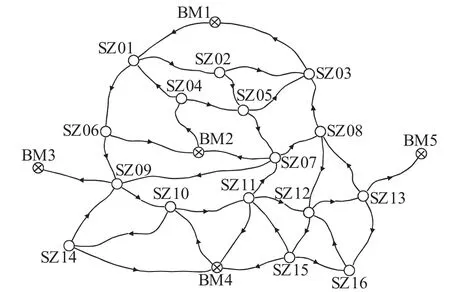
图4 二等水准网实例

通过自编程序对数据进行处理，成功搜索到全部的17个最小独立闭合环，经检核，水准网中最小独立闭合环的环线闭合差均满足二等水准测量的要求。运行程序的计算机配置为Intel酷睿i5-8250U CPU，内存频率为2 133 MHz，平均运行时间为0.01 s。为了进一步验证搜索结果，采用传统的COSA软件进行闭合差检核也得到了相同的结果。

4 结束语

本文提出了基于广度优先的最小独立闭合环搜索算法，针对基于单一的广度优先进行最小独立闭合环搜索时可能会遗漏最小独立闭合环的问题，在广度优先搜索中嵌入了“深度搜索”的过程，最后的实例验证表明本文提出的算法能够在较短的时间内正确搜索并完成水准网的环闭合差检核工作。只要稍加改进，这一算法同样也能够应用于GPS控制网和平面三角网的环闭合差检核工作。