分布式2D雷达网的航迹关联方法

谭顺成，陈中华，于洪波

(1.海军航空大学 信息融合研究所，山东 烟台 264001；2.南京电子技术研究所，江苏 南京 210039)

0 引言

雷达组网信息位置层的航迹关联，是对来自多个雷达的航迹是否对应同一目标做出判决，以保证融合中心航迹数据的同一性和完整性。目前，国内外已有许多学者对航迹关联算法进行了大量的研究，取得了大量的研究成果[1-14]，建立和发展了基于统计数学[1-2]、证据理论[3]、模糊聚类[4-5]、灰色理论[6-8]以及拓扑理论[9]等航迹关联算法体系。但是，由于2D雷达不能提供目标的高度或俯仰信息，上述航迹关联算法难以直接应用于2D雷达网，而实际的雷达网仍采用着大量的2D雷达，因此如何实现2D雷达网对空中目标的航迹关联是一个亟待解决的难点问题。

目前，对2D雷达网的研究主要集中在对空间目标的高度估计上[15-18]，并形成了2种比较常用的方法：几何法[16]和极大似然法[17-18]。几何法计算简单，但估计目标高度的离散性很大，经常找不到实数解；极大似然法理论上讲是最优的，但在具体求解时，面临着初值选择、是否收敛到全局极小点以及收敛速度等问题。文献[19]研究了基于分布式两坐标雷达网的目标3维跟踪方法，在滤波的同时实现对目标高度的估计。但是据作者所能查阅的文献，目前尚未见到关于直接利用2D雷达网对空中多目标进行航迹关联的报道。

本文从雷达网与目标的空间结构出发，提出一种基于空间几何的航迹关联算法，解决分布式2D雷达网对空中目标航迹关联问题。算法从分析两雷达航迹对应于同一目标时的几何关系出发，建立航迹关联函数，进而进行航迹粗关联和航迹精关联。在关联过程中，算法可根据雷达本身的特性自适应调整关联函数的门限值，因此算法具有较强的稳健性。

1 系统建模

1.1 雷达量测模型

考虑异地配置的2部2D雷达，令s=a,b分别表示雷达a和雷达b。假设不考虑雷达系统偏差以及地球曲率的影响，只考虑雷达随机量测误差的影响。在雷达组网系统中，雷达的观测坐标系采用本地极坐标系，在具体的某一时刻k，编号为s的雷达对目标的距离、方位角的观测值分别为r′s(k),θ′s(k)。雷达的量测值为真值与随机量测误差之和，其表达式如下

(1)

1.2 航迹关联模型

假设异地配置的2部2D雷达和目标的空间位置结构如图1所示。图中，ra和rb分别表示目标相对于雷达a和雷达b的距离，d表示雷达a和雷达b之间的距离，h表示目标的高度。在两雷达和目标组成的三角形中，βa表示雷达a和雷达b连线与雷达a和目标连线的夹角，βb表示雷达b和雷达a连线与雷达b和目标连线的夹角。在由雷达和目标在平面投影所组成的三角形中，θa,t表示目标和雷达b相对于雷达a的方位夹角，θb,t表示目标和雷达a相对于雷达b的方位夹角。且目标和雷达的方位夹角可表示为

图1 雷达网和目标的空间位置图Fig.1 Space structure of radar network and target

(2)

式中:θa表示目标相对于雷达a的方位角;θb表示目标相对于雷达b的方位角;θa,b表示雷达b相对于雷达a的方位角;θb,a表示雷达a相对于雷达b的方位角。

如图1所示，在由雷达和目标所组成的三角形中，根据余弦定理有

(3)

在雷达a和雷达b处，由立体几何的相关知识可以推导出

(4)

由于2D雷达不能测得目标的高度或俯仰信息，致使不能够采取有效的滤波方法消除雷达量测误差而不引进新的误差，这就使得在建立航迹关联模型时需要充分考虑雷达量测误差对关联的影响。目标的俯仰角可表示为

(5)

式中：φa为目标相对于雷达a的俯仰角；φb为目标相对于雷达b的俯仰角；h为目标高度。

对式(4)变形，得

(6)

式(6)表明，在没有系统偏差和雷达随机量测误差的影响下，当2部雷达观测的航迹对应于同一目标时，雷达和目标的空间位置唯一确定，可据此建立航迹关联模型

(7)

式中：i=1,…,Na表示雷达a的第i条航迹；j=1,…,Nb表示雷达b的第j条航迹；Ns表示雷达s所产生的航迹数目。显然，关联函数fa,ij(k)和函数fb,ij(k)具有相同的物理意义。

2 雷达量测噪声对关联函数的影响

将式(1)～(3)代入式(7)，有

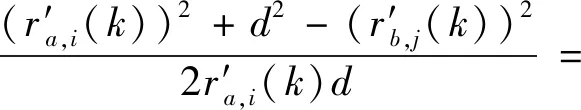
(8)

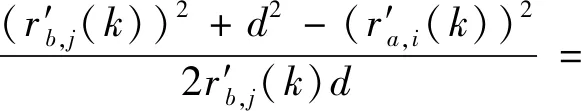
(9)

对航迹关联函数ga,ij(k)在雷达量测误差为零点进行一阶泰勒展开，有

(10)

若雷达a的航迹i和雷达b的航迹j对应于同一目标，则

(11)

式(10)可化简为

ga,ij(k)≈cosφa,isin(θa,b-θa,i(k))ξaθ+

(12)

很显然，在式(12)中ga,ij(k)是各随机变量的线性组合，而各随机变量服从零均值高斯分布，所以ga,ij(k)也服从零均值高斯分布。

同理，式(9)可以简化为

gb,ij(k)≈-cosφb,jsin(θb,j(k)-θb,a)ξaθ+

(13)

且gb,ij(k)也服从零均值高斯分布。

3 目标高度估计模型

2D雷达虽不能测得目标的高度，但依据实际情况(如利用雷达垂直面内的波束形状和雷达探测的目标距离)，可以估计出目标出现的最大可能高度hmax和最低可能高度hmin，即目标高度h应满足条件hmin≤h≤hmax。

将式(5)的代入式(12)，有

ga,ij(k)≈cosβa,isin(θa,b-θa,i(k))ξaθ+

(14)

若两航迹对应于同一目标，其关联函数值应在零附近且绝对值为最小。因此，将此时的航迹距离和方位信息代入式(14)，可得

(15)

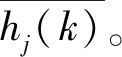
(16)

4 航迹关联

4.1 航迹粗关联

雷达的量测误差是服从零均值的高斯分布，根据高斯分布性质，雷达a的距离和方位量测误差置信水平为99.7%的置信区间分别是(-3σar,3σar]和(-3σaθ,3σaθ]。即表示在雷达a置信水平为99.7%情况下雷达的距离和方位量测误差应满足式(17)，即

(17)

同理，对雷达b置信水平为99.7%的情况下，雷达的距离和方位量测误差应满足式(18)，即

(18)

根据实际情况，雷达观测目标的俯仰信息应该满足0

|ga,ij(k)|≤3cosφa,isin(θa,b-θa,i(k))σaθ+

(19)

若雷达a的航迹i和雷达b的航迹j对应于同一目标，则函数值ga,ij(k)应满足式(20)，即

|ga,ij(k)|≤ga,ij(k)max.

(20)

同理对式(13)有

|gb,ij(k)|≤gb,ij(k)max,

(21)

且

gb,ij(k)max=3sin(θb,j(k)-θb,a)σbθ+

(22)

只有当ga,ij(k)和gb,ij(k)同时满足式(20)和式(21)，才能判定两航迹在k时刻粗关联成功，否则判定两航迹在k时刻粗关联失败。

4.2 基于历史信息的关联代价

定义从L时刻开始，若雷达a的航迹i和雷达b的航迹j在连续的M个周期内都粗关联成功，则定义在L+M时刻两航迹的关联代价为

(23)

若雷达a的航迹i和雷达b的航迹j在连续的M个周期内不能都粗关联成功，则定义在M个周期内两航迹的关联代价为cij=+∞，表示两航迹不可能是对应于同一目标。其中，αa为函数ga,ij(k)对应的权重，αb为函数gb,ij(k)对应的权重，且有

αa+αb=1.

(24)

由上文分析知ga,ij(k)和gb,ij(k)具有相同的物理意义，所以取αa=αb=0.5。在融合中心对雷达a的Na条航迹和雷达b的Nb条航迹在连续的M个周期进行航迹粗关联，可得到关联代价矩阵CNa×Nb。

4.3 航迹精关联

假定各雷达所观测的航迹不存在航迹分岔，即每个目标在雷达中都只产生一条航迹，雷达的每条航迹最多只对应于一个目标，对应的分配原如下：

(1)矩阵的每一行最多有一个元素被分配；

(2)矩阵的每一列最多有一个元素被分配；

(3)所有被分配的元素的值的总和最小。

航迹关联可以描述为如下的二维分配问题

(25)

且约束条件为

(26)

式中：ζ(i,j)=1表示雷达a的航迹i和雷达b的航迹j被分配为同一目标；ζ(i,j)=0表示不是同一目标不被关联。对于该分配问题，本文采用匈牙利算法进行求解。

5 仿真分析

设异地配置2部2D雷达，其大地坐标分别为(44°,108°,100 m)和(44°,109°,100 m)，2部雷达的采样周期均为5 s，且仿真持续时间是200 s。雷达的距离和方位量测误差都是服从零均值高斯分布，距离方差的取值范围为(100～300)m，方位方差的取值范围(0.3°～1°)。对本文算法进行仿真分析，以Ec，Ee和El分别表示航迹正确关联概率、错误关联概率以及漏关联概率，则有Ec+Ee+El=1。

图2和图3分别为30批和60批编队目标真运动图。图2中有2个编队，每个编队都有10个目标在作编队飞行，其余10个目标作杂散运动。图3有2个编队，每个编队都有20个目标在作编队飞行，其余20个目标作杂散运动。2种情况下编队飞行目标的速度是200 m/s，编队的间隔可以为500 m和1 000 m，其杂散运动目标的速度在(100～200)m/s内均匀分布，航向在(0°～360°)内均匀分布。运用Matlab进行100次蒙特卡罗仿真实验，表1和表2分别给出了粗关联周期数M=5和10时的仿真结果。

图2 30批编队运动目标真实轨迹图Fig.2 30 batches of formation targets with true tracks

图3 60批编队运动目标真实轨迹Fig.3 60 batches of formation targets with true tracks

由以上仿真结果可知：

(1)在雷达量测误差较小时，本文提出的关联算法的关联效果在各种环境下的关联效果相差不大，正确关联概率都比较高，错误关联概率比较低。

(2)由于没有对雷达航迹数据进行滤波处理，直接利用雷达的量测值进行航迹关联，在雷达的量测误差增大时，航迹正确关联概率下降明显，错误关联概率增加。

(3)缩小编队运动目标内部的编队间隔，航迹正确关联概率下降明显，且当编队间隔较小时，随着雷达量测误差的增大，错误关联概率明显增加。

(4)由表1和表2的对比可知，M=5时的算法性能优于M=10时的算法性能，其原因在于受量测误差的影响，算法很难在一个较大的周期数M内总能将两雷达测得的同一目标完全正确关联起来，因此并不是关联周期数越大算法性能越好，必须依据实际情况选取合适的关联周期数。

表1 M=5时编队运动仿真结果Table 1 Simulation results for formation targets with M=5

表2 M=10时编队运动仿真结果Table 2 Simulation results for formation targets with M=10

6 结论

本文从雷达网与目标的空间几何结构出发，针对没有系统差情况下异地配置的2部2D雷达，提出了一种基于空间几何的航迹关联算法，解决了2D雷达网对空中目标的航迹关联问题，主要包括以下内容：

(1)在空间几何的性质下，给出了2部2D雷达的航迹关联模型，该模型不需要两雷达航迹实现空间对准，避免了由于缺乏高度给坐标转换带来的误差。

(2)结合雷达量测误差的置信区间和关联函数的高斯特性给出了航迹关联的粗关联门限。

(3)基于历史信息给出了两航迹关联的关联代价，并利用航迹最优分配实现航迹的配对。

从仿真结论来看，以空间几何模型为基础，利用空间几何的相关性质建立航迹关联函数，在雷达不存在系统偏差，只有雷达量测噪声影响的情况下，本文提出的关联算法能够有效地实现两2D雷达的航迹关联，因此具有一定的工程应用价值。