重申“位置-时间关系”本质内涵的必要性——兼谈“坐标系意识”淡化的隐忧

杨振东 高寒萱

(广西师范大学物理科学与技术学院 广西 桂林 541004)

高中物理教学中，习惯性地将质点运动学中的x-t关系及其图像笼统地称为“位移-时间关系”与“位移-时间图像”；而教学实践表明，在处理部分运动学问题时，不得不将其解释为“位置-时间关系”“位置-时间图像”.如果不能对上述两种说法的联系与区别作出明确的辨析，教学中将会引发出诸多疑难问题.有鉴于此，我们从x-t关系的本质内涵出发，对其中的困惑作出澄清与讨论.

1 由“位移-时间关系”引发的困惑

如图1所示是中学阶段“追及问题”典型的x-t图像，思维缜密的学生会问：如果x-t图是位移-时间图像，那么纵轴坐标表示位移.而当t=0时x=x0，岂非意味着甲尚未开始运动却已经有了x0大小的位移？其次，t=t0时刻图像出现交点，是表示甲、乙此刻在同一位置处相遇，还是二者在这段时间内具有相同的位移？事实上，这些疑惑的本质是在追问：究竟x的本质内涵是位置还是位移？二者是不同的物理量，为什么要划上等号？平心而论，每一个具有理性思维的学生都难免产生上述疑惑，而困惑的源头正是受到“位移-时间关系”“位移-时间图像”等说法的干扰.

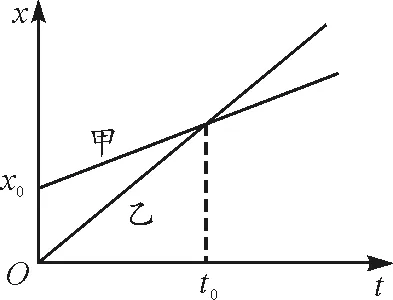
图1 追及问题中的x-t图像

毋庸讳言，这一问题不仅出现在学生中，教师群体中陷入误区的人也并不在少数.一个典型的例子是，部分教师在教学中声称“速度是位移x对时间t的一阶导数”，这也是将x与t的函数关系笼统视为“位移-时间关系”产生的典型误解，其科学性有待商榷.

2 对x-t关系本质内涵的澄清

运动学最原始的问题是如何确定物体在空间中的位置.当质点沿直线运动时，可选取该直线建立一维坐标轴.质点的位置可用坐标x表示.若质点位置发生变化，则坐标x发生相应变化.质点位置与时间的关系可表示为x=x(t)，即x-t关系.该函数关系即质点的运动学方程.需要强调的是，此处x表示质点所处位置的坐标，因此x-t本质内涵是表示质点位置坐标x随时间t的变化关系.如图2所示，t时刻物体位于x(t)位置处，经Δt时间后质点位于x(t+Δt)位置处，从x(t)处引一矢量至x(t+Δt)处，这一矢量称为位移矢量，简称位移.位移可用带正负号的量Δx=x(t+Δt)-x(t)表示.Δx为正值，位移与x轴正方向相同；Δx为负值，位移与x轴正方向相反.

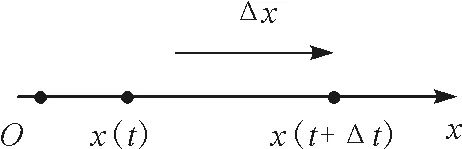
图2 一维坐标系中质点的位置与位移

如果已知质点速度随时间的变化关系v=v(t)，同时当t=0时刻质点位于x0位置处，那么可以得到其x-t关系

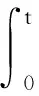
对于匀变速直线运动而言

v(t)=v0+at

上式积分结果为

这正是匀变速直线运动的运动学方程，它表明了做匀变速直线运动时，质点的位置坐标x随时间t的变化关系.

高中阶段为简化讨论，往往选择质点的初始位置作为坐标原点，即可使得x0=0，这样t时刻质点的位置坐标x(t)就能够间接表示质点在Δt时间间隔内的位移Δx.即

也就是说，这种情形下同一个物理符号x“身兼二职”，既表示其本质内涵“质点位置(坐标)”，也表示运动过程“质点的位移”.需注意的是，当且仅当初始位置作为坐标原点，即满足t=0，x=0时，“位置-时间关系”才能简化理解为“位移-时间关系”，因此不能毫无限制地将二者划上等号.事实上，这一点在2019版普通高中教科书物理必修第一册中已经作出说明：物体在每一时刻的位置或每一时间间隔的位移可以用x-t图像直观地表示，在直角坐标系中选时刻t为横轴，选位置x为纵轴，其上的图线就是位置-时间图像.如果将物体运动的初始位置作为位置坐标原点O，则位置与位移大小相等(x=Δx)，位置-时间图像就成为位移-时间图像[1].

应当承认，采取这样的简化方式将“位移”这一过程量间接通过状态函数表达出来，回避了从“位置”到“位移”的“转译”过程，在一定程度上使质点的运动学规律表现得更加精炼.然而，这也不可避免地引发负面效应——如果不加限制地将x称为“位移”，会造成对“位置”这一本质内涵的遮蔽，使学生对运动学规律停留在朦胧的、似是而非的认识阶段.如果跳出特定的适用情形，仍然持这一认识，将对学生处理问题造成困扰，甚至阻碍.这需要我们在教学中作出明确的辨析.

另一个需要澄清的问题是速度与位移间的关系.当时间间隔Δt趋近于零时，位移Δx与时间Δt的比值用以精确描述质点运动的快慢，这一极限亦可用数学中的微商表示，即

数学上将其称为x对t的导数.值得注意的是，式中的dx作为dt时间内的元位移，实际是位置坐标的微分，即

dx=x(t+dt)-x(t)

而非位移的微分.因此,严谨、科学的表述应为“速度是质点位置(坐标)x对时间t求一阶导数的结果”.对于三维空间的曲线运动，我们在建立空间直角坐标系后，往往说“速度矢量是位置矢量对时间求导的结果”，正是同样的道理.位移本身是过程量而非状态量，它不能作为时间的函数；在数学中亦不存在过程量的全微分，更无法对时间作微商运算，所谓“位移对时间求导”的说法是不科学、也不可取的，在教学中理应规避.

3 “位置-时间关系”的应用优势

不少人认为，将x-t关系解释为“位移-时间关系”，也许理解上并不严谨，但处理问题时能获得更大的便利.我们认为，这样的观点有失偏颇.在某些情况下，持“位置-时间关系”的本质理解，反而更能够简化问题求解的思路与步骤.下面以两个实际问题为例作出探讨.

【例1】物体从距地面高4.9 m处以初速度v0=9.8 m/s竖直上抛，求落地时间.

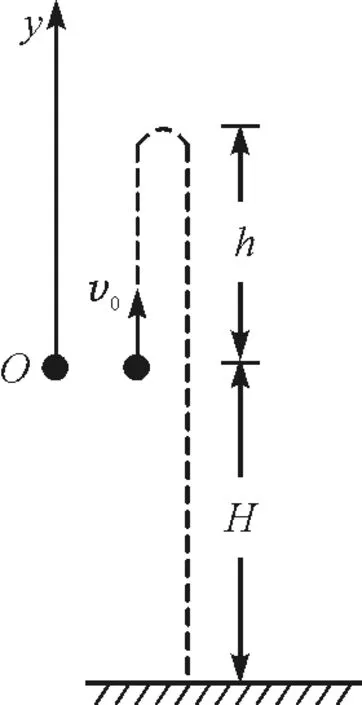
图3 竖直上抛运动

方法一：对物体运动过程进行分段处理.设物体经t1时间后到达最高点，则有

v0-gt1=0

最高点距抛出点的距离为

设物体从最高点落至地面经历时间为t2，

因此，落地时间为

方法二：如图3所示，以抛出点为坐标原点，竖直向上建立一维坐标系.则落地时刻坐标为-H，因而有

第二种方法亦被称为“坐标法”，其本质是将x-t函数关系视为“位置-时间关系”.相较之下，坐标法有效回避了对匀变速直线运动过程的考查，而能够对物体某一时刻的位置下定论，其处理问题的思路显然更具有简洁性.

【例2】在距离地面H=45 m处竖直上抛一个小球，经3 s后，在地面处以同一初速度竖直上抛一个小球.两球在离地面高度5 m处相遇.求：(1)相遇时距第二次抛出小球经过的时间；(2)抛出两球的初速度.(g取10 m/s2)

典型的思路是分阶段考虑第一个球前3 s的位移、第3 s的速度，再讨论此后两球的运动过程及相遇时各自的位移.由于运动过程涉及多个阶段，对于大部分学生而言，理清思路存在一定困难.但如果尝试用“位置-时间关系”的视角来处理这一问题，将能有效减少繁杂的分析和推理过程，问题也将迎刃而解.

解：取地面为坐标原点，向上建立一维坐标系.设初速度为v0，待求时间为t，相遇位置处的坐标为y=5 m，则有

解得

t=±1 s

舍去负根得

t=1 sv0=10 m/s

4 “坐标系意识”淡化的隐忧

事实上，当大多数人“想不到”用坐标法来处理问题时，已经昭示着我们在质点运动学章节的教学中存在某种疏漏.笔者认为，这种疏漏正是我们在处理问题时一味地用“位移”替代“位置”所致.这是因为，对于一个确定的运动过程，当参考系选定后，无论怎样建立坐标系，都不会影响到位移的大小与方向.当我们直接通过运动学公式求解出位移大小，并结合初、末位置判断出位移方向时，就逾越了建立坐标系的步骤，久而久之将造成“坐标系意识”的淡化.因此，不少人感觉到，“坐标系”仅仅作为质点运动学篇章开宗明义的第一讲，被教师以“短、平、快”的教学方式一笔带过，其后逐步消失在师生的视野中.

对于上述现象，部分教师认为，淡化坐标系的建立过程是消除冗余、“熟能生巧”之举.然而我们担忧，忽略掉必要的建系步骤会“弄巧成拙”，引起学生不良的思维“跳步”，为后续的学习埋下了隐患.这表现在3个方面.第一，在中学物理学习阶段，常用的坐标系有3种：直角坐标系、斜交坐标系、自然坐标系，在不同情境中灵活选择建系方式与坐标原点，在解决问题时可以发挥独到的作用，有效简化运算过程.用“位移”代替“位置”的做法，逾越了建立坐标系的步骤，处理问题时无疑损失了一项重要的工具.第二，涉及多个物体或多个过程的复杂运动，只有建立好确定的坐标系才能化繁为简，把一个复杂的物理过程解剖为若干部分，并就各部分遵循的物理规律列出同一个坐标系下的方程，以建立方程组进而联立求解未知量.不重视坐标系的建立，建立的方程失去了统一的标准，在联立时容易造成混乱，无疑为正确处理问题加大了阻力.第三，只有建立坐标系才能将矢量式转化为分量式，用代数运算代替矢量运算.例如，在运用动量定理时，将冲力、冲量以及初、末动量与坐标系的正方向进行比较，确定它们应取的正负号，才可列出动量定理在某一方向的分量式，将矢量运算转化为代数运算.若学生没有形成“坐标系意识”，则无法透彻理解分量式的方向性，列式时往往容易出现随意添抹正、负号的现象.

综上所述，我们认为x-t关系所体现的“位置-时间关系”是“坐标系意识”的反映，除运动学规律外，x-t关系本身还承载着更深刻的建立坐标系、精准描述物体位置的功用.因此，对“坐标系”作用的阐述绝不该一笔带过，反而应在质点运动学x-t关系的学习过程中逐步渗透、深化理解.否则学生对质点运动学规律的理解就可能是片面或畸形的，同时还会为后续学习埋下隐患.这一点希望教学者能纳入考量.