向量值BMOq,φ(X)空间上鞅算子的有界性
王汝慧
(汉江师范学院数学与计算机科学学院,湖北省十堰市茅箭区北京南路18号 442000)
1 文献综述
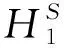
自实值鞅的研究日渐成熟之后,人们逐渐将目光转向向量值鞅。向量值鞅的研究不仅仅是实值鞅的一种自然推广,事实上,实值鞅论中的不等式和算子的有界性在向量值鞅空间中将不再成立,因此,对于向量值鞅空间及其上各类鞅算子的有界性及相关不等式的研究就成为了研究的主要方向。例如,于林、殷樱[5]研究了鞅的弱范数不等式与Banach空间几何性质的联系;刘培德[6]研究了鞅的极大算子和均方算子在向量值BMO鞅空间上的有界性;王汝慧和于林[7-8]分别研究了向量值BMOq,α(X)鞅及向量值wBMOq,α(X)鞅的鞅均方算子的有界性;于林[9]引入了一类广义的Campanato空间BMOq,φ(X),并用此空间刻画了向量值Orlicz-Hardy鞅空间HΦ(X)的共轭空间,特别地,当φ(x)=1时,这里的BMOq,φ(X)空间即为文献[3]中的BMOq(X)空间,当φ(x)=xα,p=2,且X=R时,这里的BMOq,φ(X)空间即为文献[4]中的BMOα(X)空间;Yu,Wang和Zhao[10]则研究了向量值BMOq,φ(X)鞅与有界Carleson测度的关系,但是并未研究此空间上算子的有界性。
文中主要研究鞅算子在BMOq,φ(X)鞅空间的有界性,所得结论,一方面将已有文献中的相关结论推广到更一般的空间;另一方面,也得到了Banach空间的q一致凸性及p一致光滑性新等价条件。
2 概念及引理
定义2.1[11]设f={fn,Fn,n≥1}是向量值可积适应随机变量序列,如果
fn=E(fn+1│Fn),n≥1
则称f为向量值鞅。

定义2.3[12]设{Fn,n≥1}是F的一个递增子σ-代数,使得F=∨Fn。设f={fn}n≥1是适应于{Fn}n≥1的鞅,df={dfn}n≥1为其鞅差序列,其中dfn=fn-fn-1,n≥1。为方便计,令f0≡0,F0={φ,Ω}。对于任意的0 注:对于任意L1有界的向量值函数f,对任意的n≥1,令fn=E(f|Fn),则{fn}n≥1是由f产生的关于{Fn}n≥1适应的向量值鞅,同样将其记为为f={fn}n≥1。 定义2.5设X是Banach空间,1≤q<∞,函数φ:(0,1]→(0,∞)几乎处处递增,Campanato空间BMOq,φ(X)由所有的向量值函数f∈Lq(X)组成,并且满足 ‖f‖BMOq,φ(X)∶= 注(2):当φ(r)=r0=1时,上述定义中的BMOq,φ(X)则退化成BMOq(X),即 引理2.1设X是Banach空间,1≤q<∞,函数φ:(0,1]→(0,∞)几乎处处递增,则对任意停时υ 引理2.2设X是Banach空间,1≤q<∞,函数φ:(0,1]→(0,∞)几乎处处递增,则对任意停时υ 本文中将用到已在文献[13-15]中证明的两个熟知的结论,具体如下。 引理2.3[16]若X是Banach空间,2≤q<∞,则下列3个条件相互等价: 1)X与一个q一致凸Banach空间同构; 引理2.4[16]若X是Banach空间,1≤p≤2,则下列4个条件相互等价: 1)X与一个p一致光滑Banach空间同构; 2)存在只与p有关的常数Cp>0,使得对任何向量值鞅f={fn}n≥1及∀0≤n≤m有 E(‖fm-fn‖p│Fn)≤ 3)对任何向量值鞅f={fn}n≥1,若 则{fn}n≥1依概率收敛; 4)对任何向量值鞅f={fn}n≥1,若 定理3.1若X是Banach空间,2≤q<∞,当函数φ:(0,1]→(0,1],则下列条件相互等价: 1)X与一个q一致凸Banach空间同构; 2)q阶均方算子S(q)(·)是(BMOq,φ(X),Lq(R))型的,即存在只与q,φ有关的常数Cq,φ>0,使得对任意向量值鞅f∈BMOq,φ(X)有 ‖S(q)(f)‖Lq(R)≤Cq,φ‖f‖BMOq,φ(X) (1) 证明:1)⟹2)。 设X与一个q一致凸Banach空间同构,则对于任意停时υ及任意f∈BMOq,φ(X),由引理2.3可得 ‖S(q)(f-fυ)‖Lq(R)≤Cq‖f-fυ‖Lq(X) 因为{υ=n}∈Fn,对于每一个n>0,有 所以 于是 ‖f-fυ‖Lq(X)≤Cφ‖f‖BMOq,φ(X)φ(υ<∞) ≤Cφ‖f‖BMOq,φ(X) (2) 由此可得 ‖S(q)(f)‖Lq(R)=‖S(q)(f-f0)‖Lq(R) ≤‖S(q)(f-fυ)‖Lq(R)≤Cq‖f-fυ‖Lq(X) ≤Cq,φ‖f‖BMOq,φ(X) 证明:2)⟹1)。 特别地,令φ(x)≡1,则 ‖f‖BMOq,φ(X) =2‖f‖∞≤2M<∞ 由此可知 ‖S(q)(f)‖Lq(R)≤Cq,φ‖f‖BMOq,1(X)<∞ 因此,S(q)(f)<∞几乎处处成立。由引理2.3知,X与一个q一致凸Banach空间同构。 定理3.2若X是Banach空间,1 1)X与一个p一致光滑Banach空间同构; 2)存在只与p,φ有关的常数Cp,φ>0,使得 (3) 证明:1)⟹2)。 ‖f-fυ‖Lp(X)≤Cp‖S(p)(f-fυ)‖Lp(R) 又因为 因此 ‖f‖Lp(X)≤‖f-fυ‖Lp(X) 证明:2)⟹1)。 对任意停时υ有: 特别地,令φ(x)≡1,则 特别地,令υ=0a.e.,则 推论3.1 若X是Banach空间,1 1)X与一个p一致光滑Banach空间同构; 2)存在只与p,φ有关的常数Cp,φ>0,使得 (4) 证明:1)⟹2)。 ‖f-fυ‖Lp(X)≤Cp‖S(p)(f-fυ)‖Lp(R) 又因为 ‖f‖BMOp,φ(X) ‖S(p)(f-fυ)‖p 证明:2)⟹1)。 若不等式(4)成立,由式(2)可得, ‖f-fυ‖Lp(X)≤Cφ‖f‖BMOp,φ(X) 特别地,令υ=0a.e.,则 ‖f‖Lp(X)=‖f-fυ‖Lp(X) 由定理3.2可知,X与一个p一致光滑Banach空间同构。
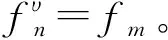
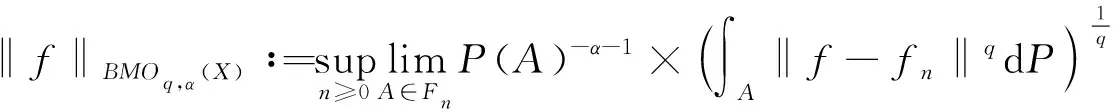
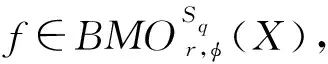

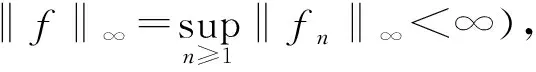

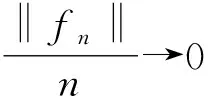
3 主要结论及证明





——以指数、对数函数同构问题为例

