笛卡尔乘积图P3×Cn的符号边控制数

汤青芽，李向军

(长江大学 信息与数学学院，湖北 荆州 434023)

引言

图的控制理论是图论研究的重要组成部分，在系统工程、通信网络、计算机与社会网络等方面中都有广泛的应用[1]。 经典的图控制理论经过不断演进和拓展，许多新的控制概念被提出和研究。 图的符号控制概念由Dnubar[2]在1995年首次提出，近些年来，符号控制研究内容也越来越丰富。 各种类型的符号控制数得到广泛的研究，如图的符号控制数[3～6]、图的符号边控制数[7～12]、图的符号全控制数[13]、图的符号圈控制数[14～16]、图的符号星控制数[17]、图的F-控制数[18，19]、图的符号边全控制数[20，21]等。 关于图的符号边控制数，徐保根[7]提出此概念，并给出了符号边控制数的一些特征刻画。 由于计算任意图的符号边控制数是十分困难的，研究某些特殊图的符号边控制数是很有意义的。 赵凌琪等[10，11]研究了一般正则图的符号边控制数的上界与下界，李向军等[22]确定了笛卡尔乘积图C3×Cn符号边控制数，徐保根等[12]给出了笛卡尔乘积图P2×Cn的符号边控制数，本文利用图结构分析方法确定笛卡尔乘积图P3×Cn的符号边控制数的确切值。

一、预备知识

记无向图G(V,E),V,E分别是图G的顶点集和边集,NG(e)表示图G中与边相邻边e的集合，NG[e]:=NG(e)∪{e}为边e的闭邻域。Cn用表示长为n的圈，P3表示顶点数为3的路。 笛卡尔乘积图G×H表示图G和图H的笛卡尔乘积，其顶点集为V(G)×V(H),对x,y∈V(G),a,b∈V(H),(x,a)与(y,b)相邻当且仅当x=y且ab∈E(H)或a=b且xy∈E(G)。 本文只考虑简单无向图，文中未说明符号和术语同文献[23]。

定义1[7]G是一个非空图，如果存在一个双值函数f:E(G)→{-1,+1}，使得对任意e∈E(G),均有∑e'∈NG[e]f(e')≥1成立，则称f为G的一个符号边控制函数。 图G的符号边控制数γ's(G)=min{∑e∈E(G)f(e):f为G的一个符号边控制函数。}

设G=P3×Cn(n≥4)，把G的顶点集看作3×n点阵，记为{xi,j:i∈{0,1,2}}，j∈{0,1,…，n-1}}，第一坐标相同的点导出图为Cn，第二坐标相同顶点导出图为P3。 根据笛卡尔乘积图的定义, 易知G是一个4-正则图。 设f为图G的一个符号边控制函数，令E+={e∈E(G)|f(e)=+1}，E-={e∈E(G)|f(e)=-1}，显然E+∪E-=E(G)，E+∩E-=Ø。令G1=(V(G),E-)为E-在G中导出子图，G1中顶点度为dG1(xi,j)。下文论述的顶点度均为G1中顶点度，下标运算均为模n算法。

二、主要结论

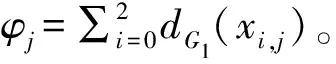
引理1 对任意j，φj≤4；若φj=φj+1=4,则,φj+2≤3,φj-1≤3。

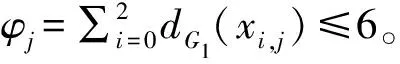
下面假设φj=φj+1,往证φj+2≤3,φj-1≤3 。 因为dG1(xi,j)≤2，所以要使φj=4，至少存在某xi,j满足dG1(xi,j)=2。

若dG1(xi,j)=2，由对称性令在E中且与x1,j的关联边为{x1,j-1xi,j，x1,jx1,j+1}或{x0,jx1,j,x1,jx2,j}或{x0,jx1,j,x,jx2,j}。 由∑e'∈NG[e]f(e')≥1易得当与x1,j关联边为{x0,jx1,j,x,jx2,j}时φj=4，其余情形φj≥3。此时dG1(x0,j)=1,dG1(x1,j)=2，dG1(x1,j)=1，所以dG1(x0,j+1)≤1，dG1(x1,j+1)≤1，dG1(x2,j+1)≤1，所以第j+1列所有点的顶点度和为至多为3，即φj+1≤3,与φj+1=4矛盾。

下面假设dG1(x0,j)=2或dG1(x2,j)=2，由其对称性不妨设为前者，令E-中与x0,j关联的边为{x0,j-1x0,j，x0,jx0,j+1}、{x0,jx0,j+1，x0,jx1,j}或{x0,j-1x0,j，x0,jx1,j}。因为∑e'∈NG[e]f(e')≥1，φj=4，在前两种情形下有φj+1≤3。 所以E-中与x0,j关联的边为{x0,j-1x0,j+1，x0,jx1,j}，因为dG1(x1,j=1)，所以dG1(x2,j)=1。若φj=4，对j+1列点顶点度进行探究，由已知有dG1(x0,j+1)=1，所以dG1(x1,j+1)≤1。要使φj+1=4，则dG1(x1,j+1)=1，dG1(x2,j+1)=2，又因为dG1(x1,j)=1，所以第j列与第j+1列边集为{x1,jx0,jx0,j+1}∪{x2,jx2,j+1x1,j+1}，此时φj=φj+1=4。 观察图G1的结构(见图1)，因为dG1(x0,j)=2，dG1(x2,j+1)=2,所以dG1(x0,j-1)=0，dG1(x2,j+2)=0,从而有φj-1≤3，φj+2≤3，引理得证。

注：粗线边、细线边分别代表和，下同。

图1φj=φj+1时图G1的局部结构

引理2 若φj=φj+1=4。且φj+2≥3，φj+3≥3,则φj+2=φj+3=3。

证明：由引理1，当φj=φj+1=4时，第j列、j+1列边集构造为{x1,jx0,jx0,j+1}∪{x2,jx2,j+1x1,j+1}。 因为φj=φj+1=4，所以由引理1得φj+3≤3，结合引理2条件得φj+2=3，所以dG1(x0,j+1)=1，dG1(x1,j+2)=2，dG1(x2,j+2)=0，且x0,j+2的关联边为{x0,j+2,x1,j+2}，x1,j+2的关联边为{x0,j+2x1,j+2,x1,j+2x1,j+3}，此时容易验证φj+3≤3，所以φj+2=φj+3=3。

引理3 对任意j,φj+φj+1+φj+2+φj+3≤14。

证明：由引理1知φj≤4。 若φj+φj+1+φj+2+φj+3中存在某元素取值至多为2，则φj+φj+1+φj+2+φj+3≤2+4×3=14；若φj+φj+1+φj+2+φj+3中所有元素取值至少为3，又由引理1、引理2得到，φj+φj+1+φj+2+φj+3中至多有两个元素取值为4，所以φj+φj+1+φj+2+φj+3≤4+4+3+3=14。

引理4 对于任意的正整数n(n≥4)，k(k≥1)当n=4k时，|E-|≤7k;当n=4k+1时，|E-|≤7k+1;当n=4k+2时，|E-|≤7k+3;当n=4k+3时，|E-|≤7k+5。

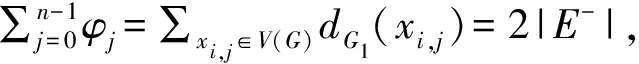
定理1对于任意的正整数n(n≥4)，整数k(k≥1)，当n=4k时，γ's(G)=6k;当n=4k+1时，γ's(G)=6k+3; 当n=4k+2时，γ's(G)=6k+4; 当n=4k+3时γ's(G)=6k+5。

证明：因为γ's(G)=|E+|-|E-|=|E(G)|-2|E-| ,所以当|E-|取上界时，γ's(G)取下界，下面给出|E-|取上界时E-的边集构造。

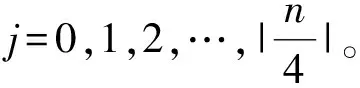
当n=4k时，由引理4，|E-|≤7k。 构造函数f为e∈W0∪W1∪…∪Wk-1时，f(e)=-1，否则f(e)=1(见图2)。 容易验证f为P3×Cn的一个符号边控制函数且|E-|=7k，结合引理4有γ's(G)=|E(G)|-2|E-|=20k-2×7k=6k。

图2 n=4k时的符号边控制函数f示意图

当n=4k+1时，构造函数f为e∈W0∪W1∪…∪Wk-1∪{x1,n-1x2,n-1}时f(e)=-1，否则f(e)=1(见图3)。 容易验证f为P3×Cn的一个符号边控制函数且|E-|=7k+1，结合引理4有γ's(G)=6k+3。

图3 n=4k+1时符号边控制函数f示意图

当n=4k+2时，令L1={x1,n-6x0,n-6x0,n-5}∪{x2,n-6x2,n-5}∪{x1,n-5x1,n-4x0,n-4}∪{x0,n-3x0,n-2x1,n-2}∪{x1,n-3x2,n-3x2,n-2}∪{x1,n-1x2,n-1}。

如果k=1，构造f为当e∈L1时，f(e)=-1，否则f(e)=1。 如果k≥2，构造f为当e∈L1∪W0∪W1∪W2∪…∪Wk-2时，f(e)=-1，否则f(e)=1(见图4)。 容易验证f为P3×Cn的一个符号边控制函数且|E-|=7k+3，结合引理4有γ's(G)=6k+4。

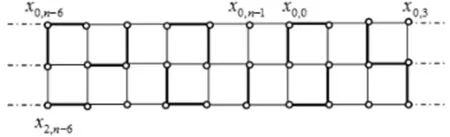
图4 n=4k+2时符号边控制函数f示意图

当n=4k+3时，令L2={x1,n-7x0,n-7x0,n-6}∪{x2,n-7x2,n-6x1,n-6}∪{x0,n-5x1,n-5x1,n-4}∪{x0,n-4x0,n-3}∪{x2,n-4x2,n-3x1,n-3}∪{x0,n-2x1,n-2x1,n-1x2,n-1}。

如果k=1，构造f为当e∈L2时，f(e)=-1，否则f(e)=1。 如果k≥2，构造f为当e∈L2∪W0∪W1∪W2∪…∪Wk-2时，f(e)=-1，否则f(e)=1(见图5)。 容易验证f为P3×Cn的一个符号边控制函数且|E-|=7k+5，结合引理4有γ's(G)=6k+5。

图5 n=4k+3时符号边控制函数f示意图

由此定理得证。

三、结语

对于笛卡尔乘积图P3×Cn, 本文通过图结构分析方式研究确定了它的符号边控制数。 对一般的m≥4，确定笛卡尔乘积图Pm×Cn的符号边控制数是值得进一步研究的问题。如果将路P3替换为一般的路Pm, 本文的提出的方法可为这类笛卡尔乘积图的符号边控制数研究提供借鉴。 对一般的笛卡尔乘积图G×H, 其符号边控制数与图G和图H的符号边控制数之间的关系也是值得进一步探讨的。