装配式钢-混凝土组合管剪力墙轴压性能与承载力计算方法研究

庞 瑞，丁书苏，王文杰，刘宇豪，徐 科

(河南工业大学土木工程学院，郑州 450001)

剪力墙作为主要抗侧力构件，广泛应用于高层建筑结构中。钢-混凝土组合剪力墙因其具备承载能力高、刚度大和抗震性能较强等特点而备受关注。目前，钢-混凝土组合剪力墙可分为型钢混凝土剪力墙、钢板混凝土剪力墙、钢管混凝土剪力墙等形式[1]。

Dan等[2]对型钢混凝土组合剪力墙进行了理论分析和试验研究，结果表明边缘构件内配置型钢可显著提高剪力墙的变形能力。吕西林等[3 − 4]对型钢混凝土剪力墙试件进行了抗震性能试验，结果表明内置型钢的剪力墙具有较好的抗震性能，并给出建议轴压比限值。王玉镯等[5]对型钢混凝土剪力墙进行了低周反复荷载试验研究，提出在剪力墙内部加入竖向平行型钢支撑可以最有效地提高剪力墙的抗震性能。梁兴文等[6]对型钢高性能混凝土剪力墙进行了低周反复荷载试验，结果表明剪跨比和轴压比是影响剪力墙延性的主要因素。伍云天等[7]对内置冷弯薄壁型钢桁架高强混凝土剪力墙进行了拟静力试验，结果表明轴压比和斜撑体积配钢率对剪力墙抗震性能有显著影响，建议控制轴压比以减小对剪力墙抗震性能的不利影响。

为了进一步提高剪力墙承载力、刚度和抗震性能，一些研究于剪力墙内设置钢板，并与墙肢端部的型钢焊接连接形成钢板-混凝土剪力墙[8]。Zhu等[9]提出带边缘钢管柱的波形钢板-混凝土组合剪力墙，进行了轴压性能试验及数值分析，并推导了承载力设计公式。王威等[10]对波纹钢板-混凝土组合剪力墙进行了低周往复加载试验和理论分析，建立了构件的抗剪承载力计算方法。郝婷玥等[11]进行了钢板-混凝土组合剪力墙轴压性能试验，研究了钢板两侧设置竖向加劲肋对组合剪力墙轴压性能的影响。上述研究表明：内置钢板可以提高剪力墙的受弯与受剪承载力，改善剪力墙的延性；与无型钢混凝土剪力墙相比，钢板混凝土组合剪力墙试件的承载能力、变形能力和耗能能力均有较大提高。

型钢混凝土剪力墙以及内置单钢板组合剪力墙中型钢或钢板未对混凝土起到足够的约束作用，结构受力效率还有提升的潜力。为此有学者提出了双钢板-混凝土组合剪力墙和钢管(束)混凝土剪力墙结构。Azree 等[12]进行了双钢板混凝土组合剪力墙轴压性能试验，研究了双钢板组合剪力墙的受力性能和破坏形态。Epackachi等[13]对4个双钢板混凝土剪力墙进行试验研究与数值模拟，提出了钢板混凝土剪力墙的简化分析模型和计算方法。张有佳等[14]进行了双钢板-混凝土组合墙轴压性能试验，给出了组合剪力墙初始刚度和极限承载力计算方法。聂建国等[15 − 16]完成了双钢板-混凝土组合剪力墙的低周反复荷载试验，分析了不同形式连接件对剪力墙抗震性能的影响。张文元等[17]进行了多腔钢管-钢管混凝土剪力墙试件的抗震性能试验，分析了结构的破坏形态和受力机理。张鹏等[18]进行了钢管束混凝土组合剪力墙的拟静力试验，研究了结构的受力性能与破坏模式。上述研究表明：双钢板或钢管可有效提高剪力墙的承载能力，使墙体具有良好的延性和耗能能力，比普通剪力墙具有更好的平面外稳定性。但双钢板-混凝土组合剪力墙和钢管束组合剪力墙大都为钢板外露，需进行专业的防火与防腐处理，增加了结构维护成本。

综上，现浇式的钢-混凝土组合剪力墙虽具备较好的延性及承载性能，但因其施工过程中存在大量现场作业和湿作业，建造周期长，环保效果差，不能满足高效和低碳的发展要求，而装配式钢-混凝土组合剪力墙则同时具备良好的结构性能和优越的经济效益，是目前发展的趋势。Wu等[19]提出装配式钢管混凝土边框剪力墙，上、下层通过短钢管螺纹连接，并采取传统竖向钢筋埋入式连接和相应构造措施。研究结果表明：影响该装配式钢管混凝土边框剪力墙抗震性能及整体性的关键因素为接缝位置处的抗震性能。童根树等[20]提出了装配式钢管束混凝土剪力墙，剪力墙上预留牛腿，钢管束混凝土剪力墙各部分通过连接件采用螺栓连接，剪力墙自重轻、抗震性能好、工业化程度高。熊枫[21]提出了装配式双钢管混凝土组合剪力墙，采用“部分装配，部分现浇”的组合方式。研究表明：此类装配式双钢管混凝土组合剪力墙的竖向连接方式可以有效地传递剪力。

在前述研究基础上，课题组提出了装配式钢-混凝土组合管(SRCT)剪力墙结构，该剪力墙集中了钢-混凝土组合结构、约束混凝土和干连接装配式建筑结构等突出优势，其构造如图1所示。

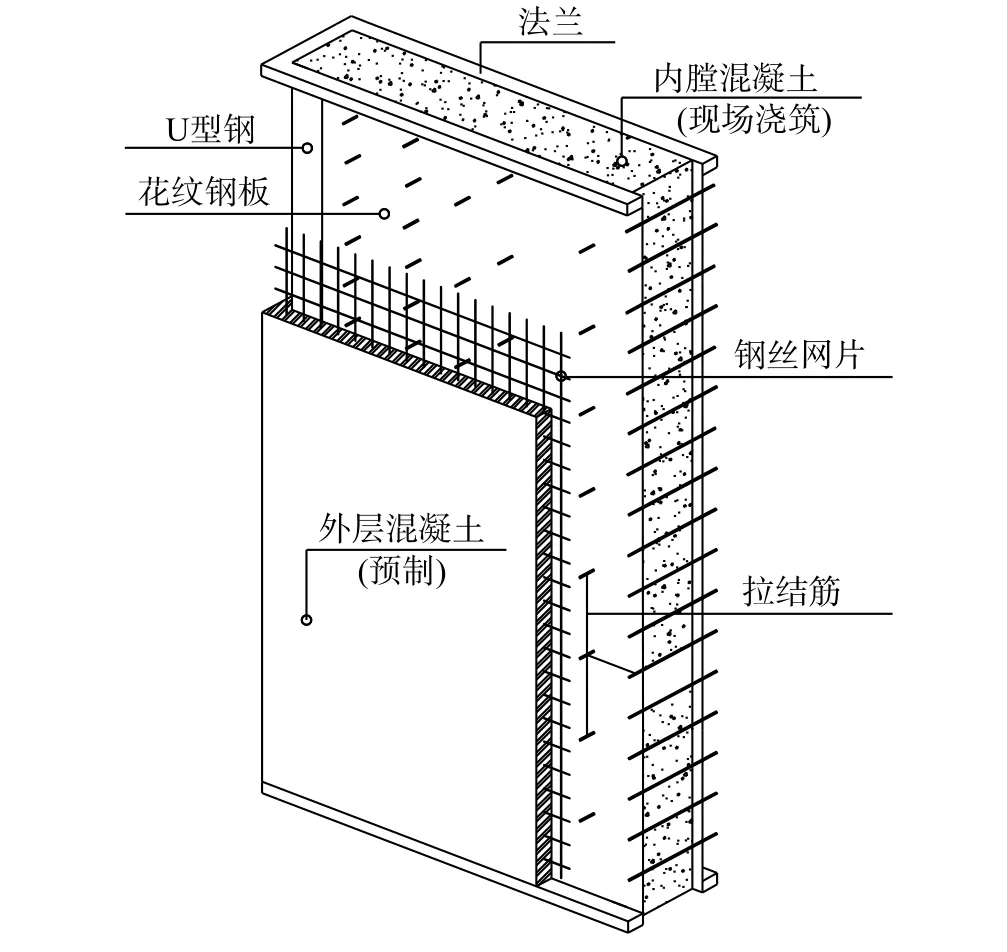
图1 SRCT剪力墙结构示意图Fig.1 Sketch of SRCT shear wall

SRCT剪力墙由工厂预制的钢-混凝土组合管和现场浇筑的管内混凝土两部分组成。现场安装时先将预制墙段通过水平和竖向连接节点可靠连接，而后在内膛浇筑混凝土形成整体，共同承担竖向和水平荷载。

构件中的U型钢与双钢板焊接为方形钢管，代替了RC剪力墙中的钢筋参与受力。双钢板间设置的拉结筋，有3方面作用：1)作为双钢板间的支撑，方便方钢管工厂制作；2)增加钢板与内外混凝土的粘结作用，协同钢板与内外混凝土受力；3)与SRCT一起约束管内混凝土受压变形。U型钢侧面焊接锚栓，协同U型钢和混凝土共同受力。中空预制钢-混凝土组合管(即SRCT)具有质量轻，便于运输和安装等特点。SRCT剪力墙外设置的混凝土保护层，提高结构的抗火与抗腐蚀性能，并与拉结筋、内膛混凝土一起抑制钢板屈曲。SRCT剪力墙上、下两端设置法兰，采用焊接或螺栓连接的方式与上、下部墙肢连接。

为研究SRCT剪力墙的轴压性能，设计了7个SRCT剪力墙，通过轴压性能试验研究距厚比、拉结筋布置方式以及U型钢侧面锚栓布置形式对SRCT剪力墙轴压承载能力、初始刚度和位移延性等轴压性能的影响，以期为SRCT剪力墙结构的研究和应用提供依据。

1 轴压性能试验研究

1.1 试验概况

1.1.1 试件设计

设计制作了7个SRCT剪力墙试件，试件尺寸为1200 mm×1000 mm×200 mm(高×长×厚)。钢板采用Q235级花纹钢板；U型规格为[14a槽钢；拉结筋贯穿钢管壁并外露20 mm。方钢管端部设置“L”型法兰，型号为L100×30×6。U型钢上布置锚栓，型号为C16，竖向间距120 mm，短锚栓长度为50 mm，长锚栓长度为240 mm。3 mm直径钢丝网规格为60 mm×60 mm。U型钢与钢板采用焊接连接，法兰与钢板间采用锚栓与焊缝相结合的连接方式。

各试件的主要设计参数如表1所示，试件几何尺寸及构造如图2所示。

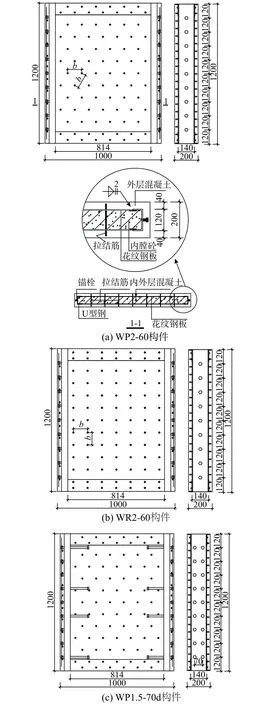
图2 试件几何尺寸及构造 /mm Fig.2 Dimensions and details of specimens

表1 试验主要参数Table 1 Main test parameters

试件编号“WP/R A-B(d)”，P为拉结筋梅花形布置，R为拉结筋矩形布置；A为钢板厚度；B为距厚比；d代表侧面长锚栓，无此项为单排短锚栓。

1.1.2 试件制作

试件制作在工厂完成。钢部件部分制作时，首先在钢板冲出与拉结筋匹配的带丝孔洞，带丝拉结筋旋入钢板，将双钢板固定，而后将槽钢翼缘端部与钢板焊接，最后将双钢板端部与L形法兰螺栓连接。钢结构部分制作完成后，在设计位置布置应变片、绑接钢丝网片、分批浇筑外皮混凝土，养护后至混凝土达到一定强度后，浇筑内膛混凝土，养护28 d。制作过程如图3所示。

图3 试件制作过程Fig.3 Production process of specimens

1.1.3 材料性能

采用设计强度等级为C35的自密实混凝土，每批试件浇筑时根据《普通混凝土拌合物性能试验方法标准》[22]取样制作了3组尺寸为100 mm×100 mm×100 mm混凝土立方体试块，与试件在同等条件下养护。依据国家标准《普通混凝土力学性能试验方法标准》[23]，测得每批混凝土强度如表2所示。

表2 混凝土力学性能Table 2 Mechanical properties of concrete

钢材材性由标准拉伸试验确定，每类钢材制作每组3个标准试样，依据国家标准《金属材料室温拉伸试验方法》[24]，测得各项参数见表3。

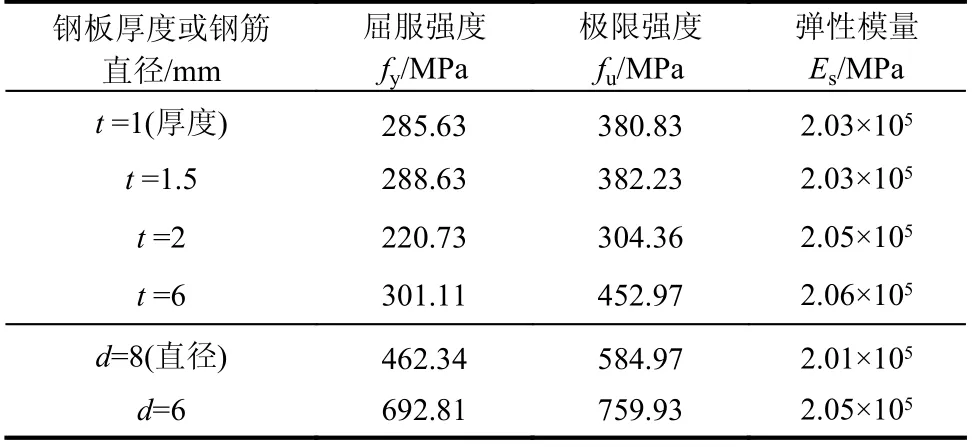
表3 钢材力学性能Table 3 Mechanical properties of steel

1.1.4 加载装置及加载制度

采用微机控制电液伺服12 000 kN压剪试验机加载，试验加载装置如图4所示。在试件上、下端均铺3 mm厚细砂，保证试件受力均匀，避免两端混凝土局部受压破坏。

图4 试验加载装置Fig.4 Test setup

采用力与位移控制相结合的加载方法进行试验。具体实施步骤：1)分三级进行弹性预压，每级荷载为300 kN；2)采用荷载控制加载，试件开裂前每级荷载为500 kN，试件开裂后，每级荷载为300 kN；3)试件屈服后，采用位移控制加载，每级位移为0.5 mm，直至试件承载力下降至峰值荷载的85%以下，结束试验。每级加载结束持荷10 min，而后观测试验现象，记录试验数据。

1.1.5 量测内容及测点布置

需要量测的物理量包括荷载、竖向相对位移、平面外变形和应变等。采用试验机内置的压力传感器测量竖向力。采用8个位移计测量试验机上、下台面间竖向相对变形，采用10个位移计测量墙的平面外变形。荷载由长柱压力机的控制微机通过传感器直接获得，位移、应变值由DH3816多测点静态数据采集系统采集。位移计、混凝土、钢板、拉结筋的应变测点布置如图5所示。

图5 试件测点布置Fig.5 Arrangement of measuring points

1.2 试验现象与破坏形态

SRCT剪力墙在轴向荷载作用下的受力过程如图6所示，可以分为以下四个阶段：

图6 典型受力全过程图Fig.6 Typical loading process

第一阶段(OA)：试件荷载-位移曲线呈线性上升，此时荷载主要由混凝土和钢管共同承担，试件各部分各自受力，变形协调，试件处于弹性工作阶段。

第二阶段(AB)：试件荷载-位移曲线斜率较OA段增大，试件刚度短暂提高。其原因为钢材的泊松比大于混凝土，使钢管与内膛混凝土有分离的趋势[25]，外层混凝土和拉结筋抑制了钢管与内膛混凝土的互相分离，内膛混凝土处于三向受压的应力状态，钢与混凝土间的组合作用开始发挥。此时，外层混凝土在钢板与U型钢焊接处、锚栓所在的竖平面处出现了竖向裂缝，试件总体上处于弹性工作阶段。

第三阶段(BC)：试件的荷载-位移曲线呈现出非线性响应。剪力墙试件面外变形加速，钢管和拉结筋开始屈服，钢管由承受轴向压应力为主变为承受环向拉应力为主，出现应力重分布，试件承载力增速变缓[26]。钢管与拉结筋对内膛混凝土的约束作用降低，试件刚度开始减小，刚度退化速度随约束作用的减弱而逐渐加快，试件进入弹塑性工作状态。当接近峰值荷载时，试件端部混凝土外鼓，部分试件中部出现横向裂缝，如图7(b)所示。

图7 试件典型破坏形态Fig.7 Failure mode of specimens

第四阶段(CD)：试件承载力达到峰值荷载后开始下降，之后趋于平缓，下降至峰值荷载的85%以下，试件破坏。在这一阶段，试件轴向变形增加明显，保护层混凝土大面积开裂、外鼓。

1.3 荷载-位移曲线

图8为不同距厚比、拉结筋布置形式、锚栓布置形式条件下各试件的轴向荷载-位移曲线。图中，荷载为轴向荷载，受压时为正值；位移为位移计实测轴向位移的平均值，压缩时为正值。

各试件主要阶段试验结果见表4。表中Nc、Ny、Nu、Nd分别为试件初裂荷载、屈服荷载、峰值荷载、极限荷载，Δc、Δy、Δu、Δd分别为与Nc、Ny、Nu、Nd对应的轴向变形。延性系数定义为极限位移与屈服位移的比值。

1) 距厚比

由图8(a)和表4可以可知，距厚比从40增加到70，峰值荷载由11 625.28 kN下降至7894.12 kN，降幅为32.1%；初始刚度由6811.00 kN/mm下降至6308.62 kN/mm，降幅为7.3%；延性系数由1.47上升至1.58，增幅为7.5%。由此可知，随距厚比增大，钢板更易发生屈曲，钢管对内膛混凝土约束作用降低，SRCT剪力墙的轴压承载能力及初始刚度与距厚比成反比，延性与距厚比成正比。

图8 荷载-位移曲线Fig.8 Load-displacement curves

2) 拉结筋布置

WP2-60试件拉结筋为梅花形布置，WR2-60试件拉结筋为矩形布置。由图8(b)和表4可知，拉结筋布置由梅花形变为矩形，峰值荷载由10 158.36 kN下降至9333.64 kN，降幅为8.1%；试件初始刚度基本相同。由此可知，拉结筋梅花形布置的SRCT剪力墙较拉结筋矩形布置的SRCT剪力墙有更好的承载力；拉结筋布置形式对试件初始刚度影响相对较小。这是由于，相同距厚比下，拉结筋梅花形布置的构件，拉结筋间的竖向间距较，对钢板的约束更强。

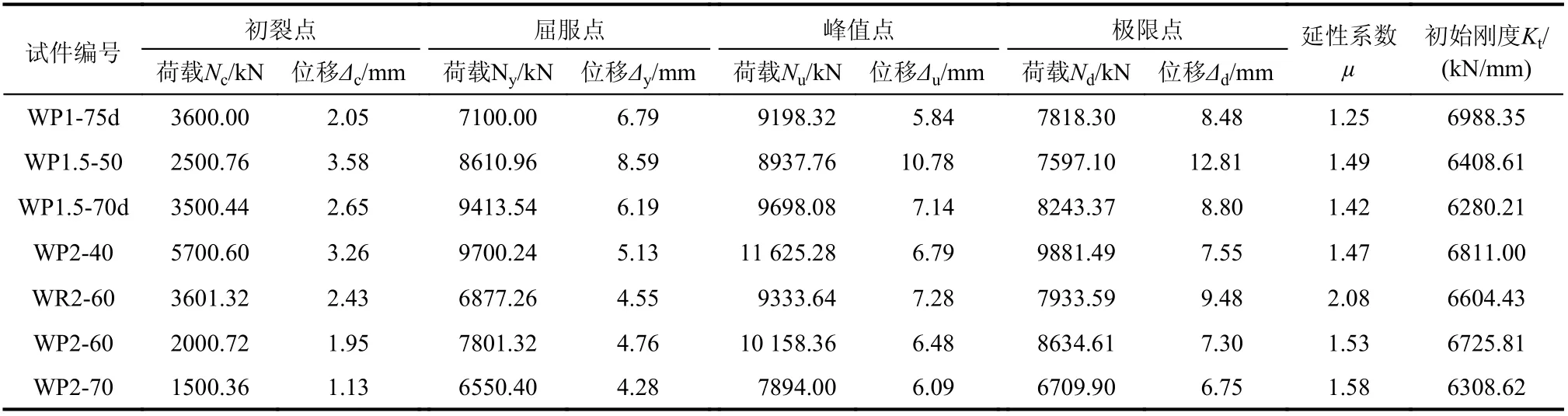
表4 主要阶段试验结果Table 4 Test results at main stages

3) 侧面锚栓

WP1-75d试件侧面有8组双排长锚栓，WP1.5-70d试件侧面有4组双排长锚栓，WP1.5-50试件侧面锚栓为单排短锚栓。由图8(b)和表4可知，侧面锚栓由单排短锚栓变为双排长锚栓，峰值荷载由8937.76 kN上升至9198.32 kN，增幅为2.9%，由前述分析可知，试件的承载能力与距厚比成反比，延性与距厚比成正比，WP1.5-75d试件、WP1.5-70d试件矩厚比均大于WP1.5-50试件，但承载力高于WP1.5-50试件，说明侧面锚栓的加强对试件承载力影响较大。其原因在于，随着侧面锚栓的加强并穿过槽钢伸入内膛混凝土，槽钢横向位移被抑制，其强度得以发挥更充分。

综上，较小的距厚比、梅花形布置拉结筋、槽钢侧面采用双排长锚栓是提高SRCT剪力墙轴压性能的有效途径。

1.4 应变分析

为研究构件的破坏特征，以WP1-75d和WP2-60试件为例，对墙体各部分应变进行分析。

1)由图9(a)和图10(a)可知，加载初期，剪力墙端部距边缘100 mm(测点C3)处应变发展迅速，这是由于，此处为U型钢与花纹钢板焊接处，两种材料刚度不同，加载时两者产生的变形量不同，出现应力集中现象，随着混凝土开裂，应力逐渐减小。由于两端混凝土过早出现裂缝，如图9(d)和图10(d)所示，加载后期，墙体中部混凝土应变值大于两端混凝土应变值。

2)由图9(b)和图10(b)可知，除图10(b)中测点U5(考虑为试件制作时存在初始缺陷)外，约0.4Nu(Nu为峰值荷载)时，荷载-应变曲线的斜率开始减小；在荷载增加至0.65Nu附近时，部分测点应变出现转折，由压应力变为拉应力，此时大部分测点应变发展略有放缓，但应变继续增长。

3)由图9(c)和图10(c)可知，加载过程中各拉结筋均受拉，表明钢板始终有外鼓趋势。加载初期，竖向荷载较小，拉结筋应力发展缓慢；随着荷载的增加，拉结筋应力发展迅速。拉结筋贯穿钢板与内、外层混凝土，设计中应使拉结筋屈服晚于构件破坏，以保证拉结筋对钢板的拉结作用和对内膛混凝土的有效约束。加载至峰值荷载时，所有拉结筋均未达到屈服强度；临近破坏时仅有少数拉结筋屈服，拉结筋设计合理。

4)由图9(d)～图9(f)、图10(d)～图10(f)可知，加载初期，试件中部横截面处混凝土、钢管、拉结筋应变基本一致，分布较为均匀；加载后期，各级荷载下混凝土、方钢管、拉结筋沿截面的应变分布规律一致，说明SRCT剪力墙结构形式可有效保障各组成部分在轴压荷载作用下的协同工作。

图9 试件WP1-75d荷载-应变曲线Fig.9 Force-strain relationship of WP1-75d

图10 试件WP2-60荷载-应变曲线Fig.10 Force-strain relationship of specimen WP2-60

2 轴压性能理论研究

2.1 初始刚度

初始刚度是结构设计的重要参数，在弹性阶段，SRCT剪力墙的初始刚度由方钢管和混凝土的轴压刚度组合而成，可由刚度叠加法计算[14]：

式中：Kc为试件理论初始刚度；Ec1、Ec2分别为外层和内膛混凝土弹性模量；Es1、Es2分别为钢板和U型钢弹性模量；h为SRCT剪力墙的计算高度。

初始刚度试验值可由布置在钢管上的若干纵向应变片在弹性阶段实测值的平均值通过算式(2)计算：

式中：Kt为试件试验初始刚度；N为竖向荷载值；ε为应变。

SRCT剪力墙初始刚度计算值与试验实测值对比详见表5。对比分析可知，计算值与试验值的比值在0.93～1.00范围内，二者吻合较好，且计算值偏小，说明在考察的参数范围内，“刚度叠加法”可较好地应用于SRCT剪力墙初始轴向刚度的计算。

表5 初始刚度计算值与试验值比较Table 5 Comparison between calculated values and test values of K

2.2 轴压承载力计算

2.2.1 钢板屈曲对钢板承载力的影响

钢板受压可能屈曲，此时两侧非受载纵边产生弯曲，屈曲处中部挠度大于两端挠度，截面应力发生重分布，中部应力不再增大，两端应力继续增加。若钢板屈曲先于屈服发生，钢材性能不能充分发挥，因此在计算钢管部分的承载力时需考虑钢板屈曲对承载力的影响。若钢板临界屈曲应力小于屈服强度，可近似认为当试件达到极限荷载时，钢板强度只在两端各be/2范围内能充分发挥，称为钢板的有效宽度。文献[27]研究了竖向荷载下钢管混凝土柱极限强度，并建议了有效宽度公式(见图11)：

图11 板的有效截面Fig.11 Effective cross-section of plate

式中：beff为钢板有效宽度；σcr为钢板屈曲应力；b为拉结筋间距。

SRCT剪力墙双钢板间设置拉结筋，将钢板分为若干钢板区格，取矩形布置形式分析，如图12所示，可得钢板的临界屈曲应力为[28]：

图12 钢板区格受力示意图Fig.12 Schematic diagram of steel plate stress

式中：D为钢板抗弯刚度；ds为钢板厚度；ν为钢板泊松比。

综上，钢管的受压承载力为：

式中：n1、n2分别为钢板和U型钢截面区格数；fys1、fys2分别为钢板和U型钢的屈服强度。

2.2.2 钢板受力分析

在轴向压力的作用下，钢管既纵向受压，同时也受到来自混凝土的横向挤压，处于纵向受压而横向受拉的三向应力状态。沿试件的宽度方向和厚度方向各取一受力分离体，如图13所示，其中：fl1、fl2分别为钢管长边、短边平均侧向约束力；fsr1、fsr2分别为长边、短边钢管的环向应力；Fs为拉结筋对钢板提供的约束力。由力平衡条件可得长边的侧向平均约束力：

图13 钢管侧向受力图Fig.13 Lateral actions of steel plates

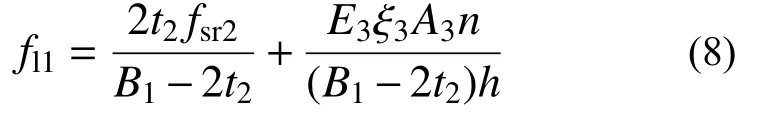
短边的侧向平均约束应力fl2为：

式中：t1、t2分别为钢板、U型钢厚度；E3为拉结筋弹性模量；ξ3为拉结筋屈服应变；A3为拉结筋横截面积；n为拉结筋数量；B1、B2分别为钢管长、短边长度。

侧向压应力相对纵向压应力和环向拉应力数值较小，可忽略。假定钢管处于平面应力状态，根据Von Mises屈服条件有：

钢管宽厚比参数R[29]是影响SRCT剪力墙破坏模态的主要因素，当R>0.85时试件将发生局部屈曲破坏；当R≤0.85时，试件可不考虑局部屈曲。分别定义钢板、U型钢宽厚比参数R1、R2为：

计算得：R1>0.85，

R2≤0.85，fa2的取值按文献[30]确定：

2.2.3 内膛混凝土受力分析

SRCT剪力墙内膛混凝土受力机理与箍筋约束混凝土类似：钢管代替纵筋和箍筋的作用；拉结筋通过约束侧向钢板，代替横向箍筋对纵筋的作用，共同对内膛混凝土提供横向约束。

剪力墙均匀受压状态下，拉结筋对核心混凝土的横向约束是间断的，核心混凝土被分为强约束区和弱约束区，如图14所示。引入横向等效约束系数ke[31]，对fl1、fl2进行折减，将混凝土对钢板的侧向压应力视为均匀分布。

图14 混凝土约束区示意图Fig.14 Diagram of confined concrete

式中：Ae1、Ae2分别为内膛混凝土横截面和侧面有效约束区的面积；Acc1、Acc2分别为内膛混凝土横截面面积和侧面面积。拉结筋对混凝土的有效约束面的边界线为抛物线，抛物线的切角θ取为0.21 rad[31]。

钢管长、短边对核心混凝土的约束作用不同，内膛混凝土在破坏时处于真三轴受压状态(fl1≠fl2)。根据文献[32]建议的混凝土五参数破坏准则，求解SRCT剪力墙内膛混凝土轴心抗压强度fcc，表达式如下：

式中：σoct、τoct分别为八面体正应力和剪应力；σ0、τ0分别为八面体正应力、剪应力相对值；α为偏平面夹角。

则内膛混凝土的轴压承载力为：

SRCT剪力墙轴压承载力由外层混凝土、钢管和内膛混凝土三部分提供，叠加各部分承载力，可得：

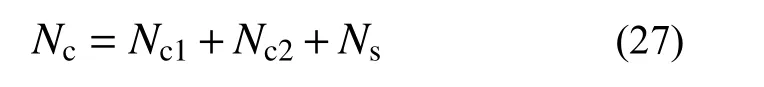
式中，Nc1为外层混凝土轴压承载力。

2.2.4 其他计算方法计算轴压承载力

目前国内外有关钢-混凝土组合剪力墙轴压承载力的计算主要有叠加原理和统一原理两种方法，为验证本文提出的SRCT剪力墙轴压承载力计算公式的适用性，参考统一强度理论[33 − 34]和叠加强度理论[35 − 36]分别进行计算。

1)中国国家标准(GJB 4142−2000)

GJB 4142−2000建议的钢-混凝土组合剪力墙轴压承载力NGJB，计算如下：

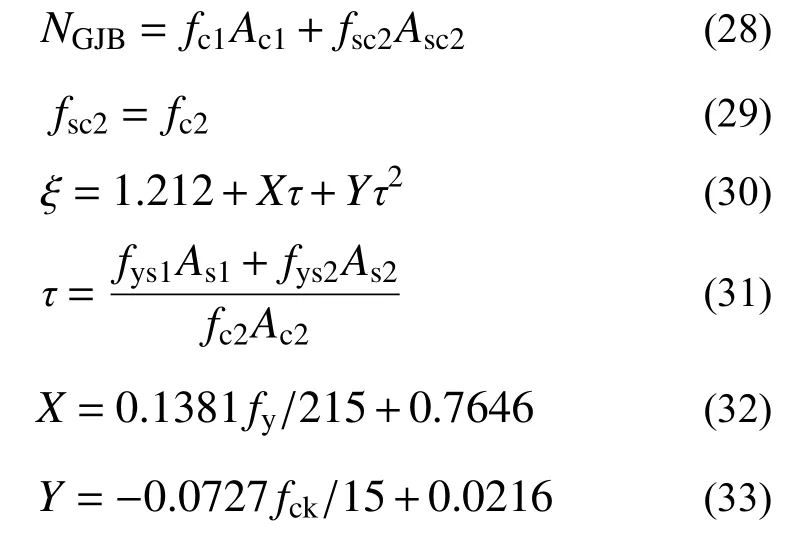
式中：ξ为约束区混凝土强度提高系数；X、Y为截面形状对混凝土强度提高系数的影响系数。

2)中国推荐标准(CECS 28：2014)

CECS 28建议的钢-混凝土组合剪力墙轴压承载力NCECS，计算同式(26)～式(29)，其他参数如下：

3)欧洲标准(EC4)

EC4中，钢-混凝土组合剪力墙轴压承载力NEC4，计算如下：

4)中国行业标准(JGJ/T 380−2015)

JGJ/T 380−2015中，钢-混凝土组合剪力墙轴压承载力NJGJ，计算如下：

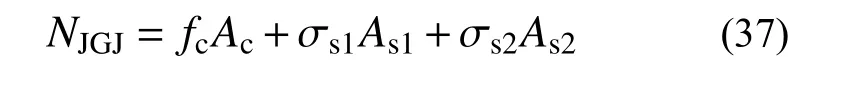
根据上述规程，利用实测材料强度，计算得到各试件的轴压承载力，计算结果见表6。图15为试验值与各规程计算结果的比值分布关系。由图15和表6、表7可知，上述标准建议方法的计算结果均较为保守，且偏差较大。其原因在于SRCT剪力墙加载前期由钢管和混凝土截面共同承担荷载，加载后期钢管截面承担更多的环向拉应力，提供侧向约束使混凝土承受更大的轴向荷载，而上述方法对这一作用考虑较少。本文建议的计算方法合理考虑了钢板局部屈曲对轴压承载力的影响和钢管约束作用对核心混凝土抗压强度的提高，SRCT轴压承载力计算值与试验值吻合较好，且数据最为集中、稳定性好，可采用推荐方法进行SRCT剪力墙轴压承载力计算，建议方法适用于带拉结筋约束的钢-混凝土组合管剪力墙轴压承载力计算。

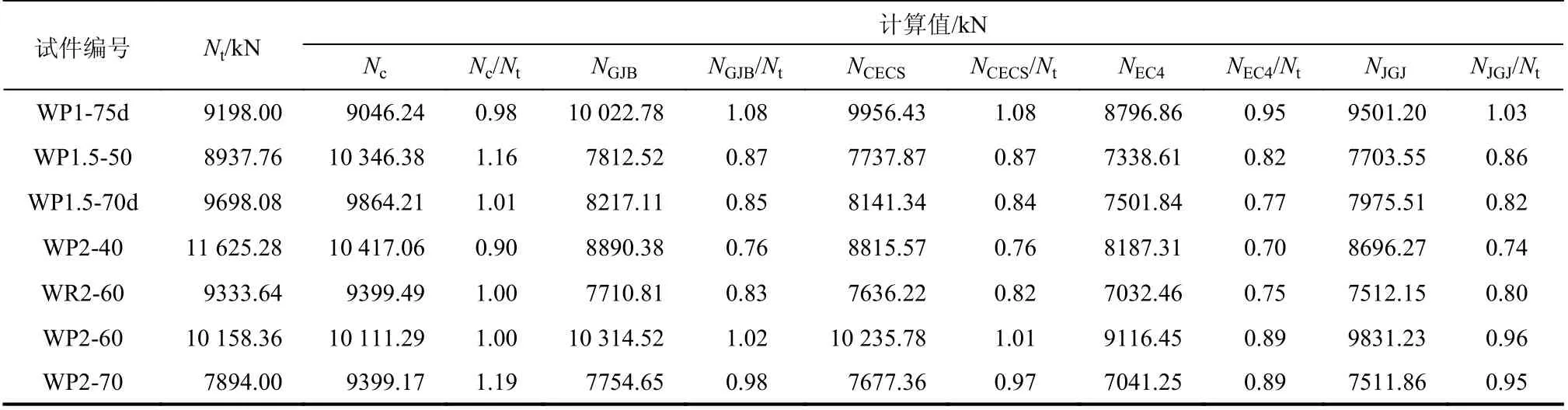
表7 承载力计算值与试验值比较Table 7 Comparison between calculated values and test values of N

图15 计算值与试验值的比值分布图Fig.15 Distribution of the ratio of calculated values to test

表6 比值平均值与离散系数Table 6 Average value and dispersion coefficient of ratio

3 结论

通过SRCT剪力墙轴压试验，分析了距厚比、拉结筋布置形式、侧面锚栓布置形式对SRCT剪力墙轴压性能的影响，参考现有规范，建立了SRCT剪力墙初始刚度、轴压承载力计算模型与计算方法，主要结论如下：

(1) SRCT剪力墙受力过程中，外层混凝土、焊接方钢管、内膛混凝土三部分协同受力，表现出良好轴压受力性能。

(2)距厚比是影响SRCT剪力墙轴压性能的重要因素，SRCT剪力墙轴压承载力、初始刚度随距厚比增加而减小，延性随距厚比增加而增大。

(3)梅花形布置拉结筋的SRCT剪力墙试件较拉结筋矩形布置的试件有更好的承载力，拉结筋布置形式对试件刚度影响较小。

(4)侧面锚栓布置形式对试件承载力有较大影响，随着侧面锚栓的加强，试件的轴压承载能力增强。

(5)建立了考虑钢板局部屈曲和钢管对核心区混凝土约束作用的SRCT剪力墙竖向初始刚度与承载力分析模型，提出了SRCT剪力墙初始刚度与承载力计算方法，计算值与试验值吻合良好。