薄钢板自攻螺钉连接受剪性能与力学模型研究
袁焕鑫,蔡康毅,吴杨威,杜新喜
(武汉大学土木建筑工程学院岩土与结构工程安全湖北省重点实验室,湖北,武汉 430072)
自攻螺钉连接具有安装便捷、成本低廉等优点,是冷弯薄壁型钢结构中普遍采用的一种连接形式,其受剪性能对冷弯薄壁型钢结构的整体性能具有重要影响[1−3]。国内外学者对自攻螺钉连接已开展了较多研究:李元齐等[1]、石宇等[4]和郝际平等[5]分别对钢板与钢板、钢板与非钢板之间的自攻螺钉连接进行了试验研究,得到了多种几何与材料因素对连接受剪承载力和失效模式的影响规律;Roy等[6]、Huynh等[7−8]通过试验探究了自攻螺钉连接的受剪性能,同时建立了合理的有限元模型;Moen等[9]完成了冷成型钢结构中自攻螺钉连接的受剪试验,提出了一种受剪变形理论模型,但未建立完整的数学表达,无法用于连接的荷载-变形关系预测。从当前公开发表的文献来看,由于自攻螺钉连接的工作机理复杂,存在材料损伤和接触变化等问题,目前对其受剪性能尤其是剪力作用下的荷载-变形关系的研究仍有不足。已有研究主要通过开展试验或数值模拟,获得自攻螺钉连接的荷载-变形曲线并作出定性或定量判断,并未对其受力机理进行深入研究,缺乏合理实用的刚度计算公式或变形力学模型。
对13组薄钢板自攻螺钉连接试件开展受剪试验,借助有限元软件ABAQUS/Explicit建立自攻螺钉连接精细有限元模型,并基于受剪试验和有限元模拟得到的荷载-变形关系曲线提出简化力学模型,为新型冷弯薄壁型钢结构构件[10−11]和结构体系的开发提供研究基础。
1 受剪试验研究
1.1 试件设计
自攻螺钉连接试件采用6类S350和S550薄钢板,钢板厚度范围为0.4 mm~2.5 mm;采用2种六角凸缘自钻自攻螺钉ST4.8×19和ST5.5×19,见表1。为探究板件厚度和螺钉直径对自攻螺钉连接受剪性能的影响,依据欧洲标准ECCS TC7 TWG 7.10[12]设计单钉连接试件13组,均为单剪连接。各组试件按图1所示代号标识,每组均包含3个相同试件。为保证螺钉与板件之间的连接可靠,应使螺钉从较薄板件一侧钻入,故规定所有试件钉帽侧板件厚度tc不得大于钉尖侧板件厚度tt。同时,由于本试验主要关注螺钉连接区域的失效情况,应避免螺钉连接发生端部撕裂,故所有试件螺钉端距均设为30 mm。

表1 试件几何尺寸Table 1 Geometric dimensions of specimens

图1 试件示意图/mmFig.1 Diagram of specimens
1.2 钢板材料力学性能
依据中国标准GB/T 228.1−2010[13]的要求,为每种规格的薄钢板加工3个相同材性试样。采用50 kN电子万能试验机开展单调拉伸试验,得到的工程应力-应变关系曲线绘于图2中,汇总得出的材料力学性能指标见表2,各指标取同组材性试样试验结果平均值。由材性试验结果可以看出:S350钢材存在明显的屈服平台和应变硬化阶段,而S550钢材没有明显的应变硬化阶段。

表 2 薄钢板材料力学性能Table 2 Material properties of thin steel sheets

图2 薄钢板应力-应变关系曲线Fig.2 Stress-strain relationship curves of thin steel sheets
1.3 加载试验
采用300 kN万能试验机开展自攻螺钉连接受剪试验,试验装置如图3所示。由试验可获得螺钉连接的荷载-变形曲线和失效模式,其中,试验荷载由试验机力传感器测得,试验变形取平行对称布置于试件两侧的位移计的平均测值。位移计通过连接杆和上、下夹具固定在试件上,夹具间距lg设为150 mm。由于螺钉连接的试验荷载最大不超过10 kN,该荷载作用下板件的拉伸变形可忽略不计,故位移计测得变形可视为螺钉连接区域的变形。为避免出现荷载偏心,在试验机夹头与试件之间增设填充板,在钉尖侧板件一端的填充板与钉帽侧板件的厚度相同且相对位置一致,反之亦然。试验采用位移控制加载,加载速率为1.0 mm/min。当试验荷载下降至峰值荷载的75%或试验变形超过15 mm时,判定试件失效。试验开始前,使用螺旋测微器分别测量试件的钉帽侧、钉尖侧板件厚度各3次,并取其平均值;正式加载前,对试验机进行平衡清零。

图3 试验装置Fig.3 Test setup
1.4 试验结果分析
自攻螺钉连接失效模式可归为5类[12],每类失效模式分别对应不同的失效特征,见表3,以此为依据分类判断试件的失效模式。统计试件的钉帽侧、钉尖侧板件厚度实测值tc、tt及对应的失效模式SExp,汇总于表4中。可以发现:本试验的13组自攻螺钉连接试件呈现出板件孔壁承压失效、螺钉剪切失效和螺钉拔出失效三种破坏模式,且螺钉拔出失效一定伴随着板件孔壁承压失效。由于螺钉连接的试验荷载较小,试件未发生板件净截面受拉失效。同时,由于试件预留了足够的螺钉端距,试件未发生板件端部剪切失效。

表3 失效模式分类Table 3 Classification of failure modes

表4 试验与模拟结果Table 4 Experimental and simulated results
典型的失效破坏照片如图4所示,分别分析这三种模式的失效破坏机理。对于板件孔壁承压失效,板件的螺钉孔由于单侧孔壁受压变形而沿传力方向伸长,随着试验荷载逐渐增大,孔壁受压侧板件材料不断压缩堆积形成褶皱,螺钉孔持续伸长直至发生最终破坏,在此过程中,板件还会发生面外翘曲且翘曲程度逐渐增大,直至临近破坏,其翘曲程度会有所减小。对于螺钉拔出失效,初始时螺钉受剪力作用开始倾斜,随着试验荷载不断增大,螺钉倾斜程度逐渐提高,且板件之间开始形成间隙并不断扩大,直至发生破坏。对于螺钉剪切失效,试件在加载过程中无明显变化,但由于螺钉被剪断而发生突然破坏。

图4 失效破坏照片Fig.4 Failure photos
对比表4各试件组的失效模式可以看出:当螺钉直径与钉帽侧板件厚度之比d/tc接近2.3时,板件与螺钉之间存在有效嵌固,而螺钉的横截面面积不足,自攻螺钉连接试件发生螺钉剪切失效;当d/tc接近或大于7.8时,钉帽侧板件厚度较小易撕裂,试件发生板件孔壁承压失效;当d/tc介于4.8~6.0时,板件与螺钉之间难以形成有效嵌固,板件螺钉孔易伸长且螺钉易被拔出,试件发生板件孔壁承压失效与螺钉拔出失效。
对同组试件相同变形对应荷载取平均值,可以绘制荷载-变形平均曲线,如图5所示。各试件组峰值荷载Fu,Exp及其对应变形Δu,Exp汇总于表4中。由图5(a)、图5(b)和图5(c)对比板件厚度的影响可知:当自攻螺钉连接试件发生板件孔壁承压失效与螺钉拔出失效时,其初始刚度、受剪承载力和延性随板件厚度的增大而提高;当连接的失效模式随着钉帽侧板件厚度的增大由板件孔壁承压失效与螺钉拔出失效转变为螺钉剪切失效时,其初始刚度随之提高,但受剪承载力和延性随之降低。由图5(d)对比螺钉直径的影响可知:当试件发生板件孔壁承压失效与螺钉拔出失效时,其初始刚度、受剪承载力随螺钉直径的增大而提高,但延性基本不变;当试件发生螺钉剪切失效(如FF1X、FF1Y试件组)时,其受剪承载力和延性随螺钉直径的增大而提高,但初始刚度基本不变。

图5 受剪试验的荷载-变形曲线Fig.5 Load-deformation curves from shear tests
2 有限元模拟
2.1 模型部件与材料属性
自攻螺钉连接的受剪变形实质上是板件与自攻螺钉发生材料渐进失效直至破坏的过程,存在材料损伤和接触变化等问题。采用ABAQUS/Explicit建立自攻螺钉连接精细有限元模型并开展非线性准静态分析。有限元模型由钉帽侧板件、钉尖侧板件、钉帽螺杆和螺纹共四个部件组成,如图6所示。钉帽侧和钉尖侧板件的长度取受剪试验的板件重叠区域长度。在建模时,自攻螺钉的几何尺寸参照中国标准GB/T 15856.5−2002[14],同时简化其次要特征,保留其关键特征,具体操作为:将螺杆简化为圆柱体,考虑钉帽承压面内凹;考虑4圈螺旋向螺纹,且螺距与实际一致。

图6 模型部件Fig.6 Parts of model
0.4 mm、0.5 mm和0.6 mm三种厚度的S350钢板在受剪试验中表现出明显的材料损伤破坏特征,建模时考虑板件的弹性性能、塑性性能和损伤性能;2.5 mm厚S350钢板、0.8 mm和1.0 mm厚S550钢板的材料损伤破坏特征不明显,仅考虑弹性性能和塑性性能。板件弹性性能采用表2中的弹性模量E和泊松比ν来描述。板件塑性性能分别由修正前、后的Ludwik本构模型拟合板件的真实应力-真实塑性应变试验曲线来描述:修正前的Ludwik本构模型适用于无明显屈服平台的材料,见式(1);修正后的Ludwik本构模型适用于有明显屈服平台的材料,见式(2)。



图7 板件塑性本构关系曲线Fig.7 Plastic constitutive relationship curves of steel sheets



图8 板件损伤本构关系曲线Fig.8 Damage consitutive relationship curves of steel sheets
参照自攻螺钉生产厂商提供的螺钉受拉、受剪试验数据,螺钉的弹性模量取206 GPa,泊松比取0.3,屈服强度取950 MPa,抗拉强度取1050 MPa,断后伸长率取1%。
2.2 单元类型与网格划分
有限元模型采用八节点线性缩减积分实体单元C3D8R。考虑到模型对网格尺寸的敏感度较高,网格尺寸通过试算对比来确定。在板件厚度方向,为避免积分点缩减可能导致的“沙漏”效应,单元数量不少于2个;在垂直板件厚度方向的平面内,单元尺寸取0.5 mm。以CE1X试件为例,按上述要求进行网格划分共得到15318个单元,如图9所示。
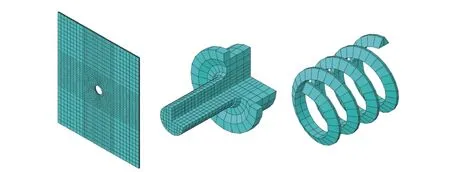
图9 单元网格划分Fig.9 Meshed elements
2.3 接触与边界条件
在螺杆和螺纹之间设置捆绑约束,其余部件之间定义通用接触。通用接触的定义包括接触表面对和接触属性。按图10定义接触表面对,其中单元表面对是指定义了损伤属性的单元自身与自身之间、自身与其他单元之间的表面对。按法向硬接触和切向库伦摩擦接触来定义接触属性,几何表面对的摩擦系数取0.25,单元表面对的摩擦系数取4.00。在钉尖侧板件设置固定约束,在钉帽侧板件设置速度和位移约束。速度约束采用点耦合的方式施加在沿板件长度方向的平动自由度上,并通过光滑型幅值曲线控制加载速率,其余方向的位移自由度均被约束限制。加载速率取200 mm/s,时间步长取0.04 s。

图10 接触表面对Fig.10 Contact pairs
2.4 有限元模型验证
将有限元模拟所得的失效模式SFE、峰值荷载Fu,FE及其对应变形Δu,FE、模拟与试验的荷载-变形上升段曲线对比得到的Pearson相关系数rFE-Exp汇总于表4中。图11和图12分别给出了部分试件组模拟与试验的荷载-变形曲线对比和失效模式对比。从表4可以看出:有限元计算得出的峰值荷载值与试验结果接近,其平均比值为0.96,标准差为0.11,但其对应变形的模拟值与试验值存在一定偏差,平均值为0.80;模拟与试验荷载-变形上升段曲线的相关度较高,相关系数的平均值为0.94;模拟与试验失效模式基本一致。因此,所建立的自攻螺钉连接精细有限元模型能够比较准确地模拟受剪试验过程,有限元模型的可靠性得到验证。

图12 模拟与试验的失效模式对比Fig.12 Comperison between simulated and experimental failure modes
3 受剪力学模型
3.1 曲线数据获取
基于验证可靠的有限元模型,借助Python编程语言实现模型的参数化,调整关键控制参数的取值并进行计算分析,从而生成大量的荷载-变形曲线数据,用来建立自攻螺钉连接受剪力学模型。控制参数包括板件厚度(0.4 mm、0.5 mm、0.6 mm、0.8 mm、1.0 mm、1.2 mm、1.5 mm、2.0 mm、2.5 mm和3.0 mm共计10种)和螺钉直径(4.2 mm、4.8 mm、5.5 mm和6.3 mm共计4种)。规定钉帽侧板件厚度不得大于钉尖侧板件厚度,板件材料属性按第2.1节取值。有限元模拟得到的荷载-变形曲线共计220组,统计各组曲线的几何与材料参数(螺钉直径、钉帽侧和钉尖侧板件的厚度以及抗拉强度)和受剪性能参数(峰值荷载及其对应变形、失效模式)。汇总试验和模拟得到的失效模式,进而分析其受螺钉直径与钉帽侧、钉尖侧板件厚度之比的影响,如图13所示。

图13 失效模式分析Fig.13 Analysis of failure modes
由图13可以发现:当螺钉直径与钉帽侧板件厚度之比d/tc<4.0时,连接发生螺钉剪切失效;当d/tc>8.0时,连接发生板件孔壁承压失效与螺钉拔出失效;当d/tc介于4.0~8.0时,三类失效模式均可能发生。由于自攻螺钉连接发生螺钉剪切失效时的荷载-变形曲线数据离散性较高,以下主要对板件厚度介于0.4 mm~3.0 mm、螺钉直径与钉帽侧板件厚度之比d/tc不小于4.0的自攻螺钉连接的荷载-变形关系建立受剪力学模型。
3.2 模型建立
自攻螺钉连接的受剪力学模型可类比本构模型分为弹性性能、塑性性能和损伤性能。其中,弹性性能采用初始刚度k0来描述;塑性性能采用荷载-变形上升段曲线来描述;损伤性能采用损伤起始判据和损伤演化法则共同描述,将损伤起始点对应变形作为损伤起始判据,由荷载-变形下降段曲线计算得到损伤演化法则。参考Hassanieh等[17]提出的钢木螺钉连接渐近线模型,建立三段式受剪力学模型,见式(5)。

式中:Fu、Δu分别为峰值荷载及其对应变形,两者满足式(6);k0为初始刚度;Fp为趋近荷载。可以发现:该受剪力学模型包括曲线上升段、峰值平行段和由上升段经对称缩放变换得到的曲线下降段,为得出该模型的完整数学表达,需分别建立初始刚度k0、趋近荷载Fp和峰值荷载Fu的计算公式。
3.3 参数确定
分析自攻螺钉连接的受剪机理可知:连接的变形主要由两部分组成,分别是由于螺钉的平动和转动引起的板件压缩变形以及由于板件的平动引起的螺钉剪切变形。以下将具体分析这两部分变形,从而建立初始刚度k0的计算公式。
图14为板件压缩变形时的受力简图,螺钉被视为刚体,板件作为线弹性体,忽略钉帽的撬力作用和螺纹的嵌固作用,且假定板件在孔壁承压处近似满足材料力学中的平截面假定和单向受力假定。

图14 板件压缩变形Fig.14 Compressive deformation of steel sheets
图14中的符号含义如下:Δc、Δc,T分别为钉帽侧板件的总变形、平动变形;Δt、Δt,T分别为钉尖侧板件的总变形、平动变形;θR为螺钉的转动角度;F为剪力;σc、σt分别为钉帽侧、钉尖侧板件孔壁承压处最大压应力。取图中钉帽侧和钉尖侧板件为脱离体,分别依据力平衡方程和本构方程建立式(7)、式(8),假定板件变形主要集中在螺钉孔附近的3倍螺钉直径范围内。

联立式(7)、式(8),求解得到钉帽侧、钉尖侧板件的总变形Δc、Δt,见式(9),Δc、Δt还可按式(10)表达。由此可求得板件压缩刚度kSh,见式(11)。


图15所示为连接在发生螺钉剪切变形时的受力简图。类似于图14,该受力简图视板件为刚体,螺钉为线弹性体,同样忽略螺钉钉帽的撬力作用和螺纹的嵌固作用。

图15 螺钉剪切变形Fig.15 Shear deformation of screw
图15中的符号含义如下:Δs为螺钉剪切变形;F为剪力;τs为螺钉剪切面处的最大剪应力。依据力平衡方程和本构方程建立式(12),求解得到螺钉剪切变形Δs,见式(13),由此可求得螺钉剪切刚度kSc,见式(14),式中螺钉剪切模量Gs=Es/2(1+νs)。

假定Ec=Et=Es=E、νc=νt=νs=ν,则式(11)、式(14)可简化为式(15)、式(16),式中剪切模量G=E/2(1+ν)。由此可建立初始刚度k0的计算公式,见式(17)。

对于趋近荷载Fp和峰值荷载Fu,可认为与中国规范GB 50018−2002[18]第6.1.7.2条文自攻螺钉连接受剪承载力计算公式存在线性相关。故按式(18)~式(20)建立趋近荷载Fp和峰值荷载Fu的计算公式。
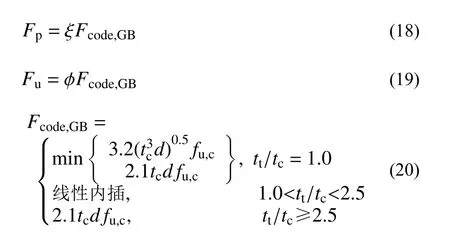
式中,fu,c为钉帽侧板件抗拉强度。需要注意的是,式(20)有别于规范公式,其采用抗拉强度实测值代替设计值,且不考虑抗力分项系数。
借助数据分析绘图软件Origin及其脚本语言Labtalk编写脚本对各计算公式的系数进行标定,各系数取值汇总于表5中。由表5可知:所建立的三段式受剪力学模型能够较好地预测自攻螺钉连接的荷载-变形受剪关系。

表5 三段式模型系数取值Table 5 Coefficient values of three-stage model
考虑到单个自攻螺钉连接的受剪承载性能与多钉连接存在显著差异[1],且实际工程中往往采用多钉连接(螺钉数目大于2),故建立的三段式受剪力学模型还应考虑群钉效应的影响。群钉效应修正系数ψ参考JGJ 227−2011[19]第6.2.1.3条文的多钉连接折减系数来计算,见式(21)。考虑群钉效应修正后的三段式模型由式(5)变换为式(22)。相应地,第3.3节推导得到的初始刚度k0、趋近荷载Fp和峰值荷载Fu也需要考虑群钉效应修正系数ψ的影响。

式中,n为螺钉数目。

3.4 模型验证
为验证三段式受剪力学模型的适用性,结合前期完成的正弦波纹腹板-管翼缘冷弯薄壁钢箱梁受剪试验[20],开展有限元模拟和试验结果对比。箱梁试件采用焊接冷弯矩形钢管作为框架、冷弯波纹钢板作为腹板,框架与腹板之间通过自攻螺钉连接。采用有限元软件ABAQUS/Explicit开展非线性准静态分析。矩形管和波纹板的材料属性分别按第2.1节中的2.5 mm和0.4 mm厚S350钢板取值。自攻螺钉连接采用连接单元模拟,单元属性依据三段式受剪力学模型计算得到的荷载-变形关系来定义。箱梁试件自攻螺钉连接的数量较多,但考虑到系数ψ的计算值随螺钉数目n的增大逐渐趋于稳定,此处近似取n=10,因此群钉效应修正系数ψ取0.7,螺钉连接的荷载-变形关系如图16所示。有限元模型其余参数,包括几何尺寸、边界条件、单元类型和网格划分等参照文献[20]设定。

图16 连接荷载-变形关系曲线Fig.16 Load-deformation relationship curve of connection
对于梁高h不同的4类正弦波纹腹板-管翼缘冷弯薄壁钢箱梁,试验和模拟得到的峰值荷载Pu,Exp、Pu,FE及其对应挠度Du,Exp、Du,FE列于表6中,试验与模拟的荷载-挠度曲线对比如图17所示。由结果对比可知:有限元模拟结果与试验结果吻合良好,因此验证了所建议的三段式受剪力学模型的适用性。

表6 模拟与试验结果比较Table 6 Comparison between simulated and experimental results

图17 模拟与试验的荷载-挠度曲线对比Fig.17 Comparison between simulated and experimental load-deflection curves
4 结论
通过试验研究、有限元模拟和理论分析,探究了薄钢板自攻螺钉连接的受剪性能,建立了用来描述自攻螺钉连接荷载-变形关系的三段式受剪力学模型,得到以下结论:
(1)自攻螺钉连接常见的失效模式有板件孔壁承压失效、螺钉拔出失效和螺钉剪切失效。当自攻螺钉连接发生板件孔壁承压失效与螺钉拔出失效时,连接的初始刚度、受剪承载力和延性随板件厚度的增大而提高,初始刚度和受剪承载力随螺钉直径的增大而提高;当连接发生螺钉剪切失效时,受剪承载力和延性随螺钉直径的增大而提高。
(2)建立了自攻螺钉连接精细有限元模型。该模型采用Johnson-Cook损伤本构和线性损伤积累法则来定义材料属性,考虑了螺钉的形貌特征,能够比较准确地模拟自攻螺钉连接受剪试验过程。
(3)基于自攻螺钉连接受剪试验和有限元模拟得到的荷载-变形曲线,提出了三段式受剪力学模型。该力学模型采用中国规范GB 50018−2002[18]的自攻螺钉连接受剪承载力计算公式,分析了板件压缩刚度和螺钉剪切刚度的影响,并考虑了螺钉的群钉效应修正。通过与试验数据对比验证了该力学模型能较好地预测自攻螺钉连接受剪的荷载-变形关系。

