基于神经网络遗传算法的深腔型零件拉深工艺参数优化

邱超斌，张猛，郎利辉，郭庆磊，江培成，李奎，陈林

（1.航空工业西安飞机工业（集团）有限责任公司，西安 710089；2.北京航空航天大学 能源与动力工程学院，北京 100191；3.北京航空航天大学 机械工程及自动化学院，北京 100191；4.天津天锻航空科技有限公司，天津 300232）

冲压作为薄壁材料塑性成形的主要方式，具有操作简单、成本低、生产周期短及材料利用率高等优点，在汽车、高铁及航空航天等运载行业有广泛应用[1—4]。据统计，在汽车制造领域，有70%以上的零件通过冲压制造[5]。结合神经网络等智能手段探究薄壁材料的冲压成形工艺是提升汽车等制造领域工艺水平的重要手段，也是实现产业升级的有效途径[6—10]。

近20 年来，随着高性能计算机的普及，有限元被广泛应用于各个领域，在金属塑性成形领域大放异彩。当前，国内外诸多学者对冲压过程中的冲压速度、摩擦因数、压边力及拉延筋分布等关键工艺参数进行了研究，发现了大量具有指导意义的规律。谢延敏[11]等以板料减薄及增厚作为输出目标，采用粒子群优化方法获取了拉延筋分布及其具体参数同输出目标的对应关系；文艺等[12]利用遗传算法及响应曲面法对成形参数进行了优化，获得了某靠背零件的最佳成形工艺参数；赵茂俞等[13]将拉延筋的凸筋高度、凸筋圆角半径、凹筋圆角半径等作为影响因素，并采取正交试验法，获得了不同水平值下的输出目标值。上述研究工作均在利用各种寻峰或优化技术的基础上，通过分析不同成形工艺参数下的大量有限元计算结果进行计算，存在工作量大、优化模型过于庞大等缺点。由于有限元技术具有计算不稳定性，其涵盖多变量优化模型的优化计算难以保证真实性及有效性，且不同零件的冲压成形工艺参数的影响“比重”又存在细微差异，因此，难以做到通用性。

为解决上述问题，文中拟以某深腔型零件为例，以壁厚变化为成形质量输出目标值，采用正交试验法获取不同因素在不同水平下的输出目标值。在此基础上，使用灰度关联分析（GS）理论对上述因素进行甄别选取，获取对输出目标影响的关键工艺参数。随后利用神经网络遗传算法进行工艺参数寻优。最后分析结果，并利用最优工艺参数对深腔型零件进行试制，以验证上述优化方法的准确性。

1 深腔型零件有限元模拟及其结果分析

1.1 零件特征及材料性能参数

某航空不锈钢深腔型零件如图1 所示，其沿长轴方向对称，长为652 mm，宽约为352 mm，最大深度为155 mm，最小圆角为3.6 mm。

图1 深腔型零件数模Fig.1 Mathematical modeling of a deep cavity drawing part

该材料为304 奥氏体不锈钢，具有塑性变形程度大、冷加工易发生硬化、拉深易褶皱等特点。对其进行单向拉伸试验，其真实应力-应变曲线如图2所示，并利用DYNAFORM 中的36#BARLAT 模型进行表征。

图2 材料应力-应变曲线Fig.2 Material stress-strain curve

1.2 有限元模型

按照一阶连续原则对该零件进行工艺面补充，由于该件沿长轴方向对称，为提升计算精度，降低计算量，采取1/2 模型进行模拟分析，其拉延筋位于凹模入口外25 mm 处，形式为圆形拉延筋，其深度为4 mm，凸筋圆角半径为4 mm，凹筋圆角半径为5 mm，凸筋宽度为11 mm。在CATIA 软件中进行上述操作，得到的有限元模型如图3 所示。

图3 有限元模型Fig.3 Finite element model

1.3 试验因子范围确定

为了更好地对成形工艺参数进行优化分析，给定了初始工艺参数，材料为Cr18Ni10N，板料厚度为1.2 mm，冲压速度为0.25 m/s，摩擦因数均为0.125，压边力为0.98 MN，模具间隙为0.12 mm。

文中研究的试验因子为（关键工艺参数）压边力、冲压速度、模具间隙及板料与模具的摩擦因数。

1.3.1 压边力范围

压边力是影响成形质量的重要参数之一，过大的压边力虽能减少褶皱的发生，但易引发局部应变过大，从而导致破裂[12]。压边力的计算方法可分为经验法和有限元软件计算法，其计算结果分别如下所示。

1）有限元软件计算法。对给定上述初始参数的有限元模型进行计算，得到了以横轴为步长时间，纵轴为压边力的压边力变化规律曲线，如图4 所示，其最大压边力为1.6737 MN。

图4 压边力预测Fig.4 Prediction of blank holder force

2）经验法。经验公式如式（1）所示。

式中：F为压边力（N）；q为板料上单位压力（MPa），大于0.5 mm 的板料一般取2～2.5 MPa，文中取q=2.5 MPa；A为压边面积，为684 856.43 mm2，计算得F=1.712 141 075 MN，约为1.712 MN。

上述2 种计算方式的结果相差小于3%，为计算方便文中取压边力为1.584 66 MN。

1.3.2 冲压速度

冲压速度在一定程度上会影响材料的塑性变形及流动，从而影响最终零件的成形质量。过大的冲压速度会导致材料流动不及时，进而出现破裂的现象；过短的冲压速度会降低生产效率，提高成本。有限元中刚性模具的加载速度一般为实际速度的10 倍[5]。结合生产平台，文中给出了5 个真实典型的冲压速度，分别为0.15，0.2，0.25，0.3，0.35 m/s。

1.3.3 模具间隙及摩擦因数

模具间隙和摩擦因数是通过改变材料在成形过程中受到的阻力，从而影响成形后零件的壁厚分布。间隙过小或摩擦因数过大会使材料受到的阻力变大，材料流动困难，进而导致壁厚分布不均；反之，会使材料易出现褶皱及贴模度差等缺陷，因此，文中间隙范围取初始板厚的10%～20%，即1.1～1.2 倍料厚。按作用区域划分，该零件的摩擦因数可分为板料与压边处摩擦因数（简称摩擦因数1）和板料与凸模处的摩擦因数（简称摩擦因数2），文中摩擦因数取成形过程中的典型数值，分别为0.05，0.125，0.15，0.17 和0.2。

1.4 成形评价指标与正交试验

1.4.1 成形评价指标

破裂是冲压工艺常见的缺陷，在其他影响因素相同的条件下，壁厚减薄量的大小能在很大程度上表征零件是否会出现破裂，因此，文中选取壁厚减薄率作为成形质量的评价指标，壁厚减薄量计算如式（2）所示。

式中：t0为板料初始厚度（mm）；t1为成形后板料壁厚（mm）。

1.4.2 正交试验设计及结果

根据1.3 节中的5 个主要试验因子及取值范围，给出表1 所示的试验因素水平。

表1 试验因素水平Tab.1 Orthogonal test factor level

根据试验因子个数及其水平数，文中选取L25(55)的正交表，其试验结果如表2 所示。由表2 可知，其壁厚增厚率均小于14%，且数值模拟结果均无起皱现象，故选取壁厚减薄量作为单一优化目标。

表2 正交试验结果Tab.2 Results of orthogonal experiment

2 灰度关联分析及参数寻优

2.1 灰度关联分析及拉丁超立方抽样

2.1.1 灰度关联分析

GS 理论是一种利用已知信息预测未知信息的方法，如果某系统属于灰度系统，则不论数据分散程度多大，各个参数均存在相关性。考虑到传统因素分析在灰度系统数据处理中的不足，采用GS 理论分析该系统的灰度关联性，以探寻不同系统因子同主行为因子的相关性，并通过出现的相似或相异度给出不同因素之间的相关程度。将GS 理论运用到板材冲压工艺中，能快速确定诸多工艺参数同优化目标之间的相关性，并给出各成形参数造成的影响“比重”[11,14]。GS理论的一般计算过程如下所示。

假设有序列y=(y(1),y(2),...,y(n))，利用式（3）获取各参数的标准化分布。

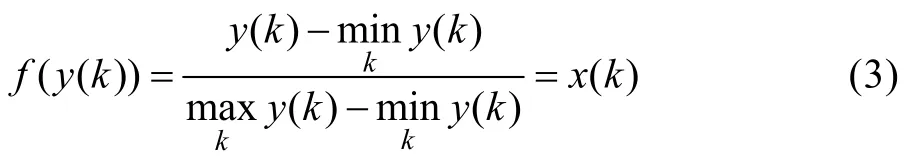
选取参考序列x0=｛x0(k)|k=1,2,3,...,n｝，其中k为时刻，假设有m个序列，则定义式（4）为xi对参考序列x0在k时刻的关联系数。

式中：数据归一化采取均值法以降低不同单位对其关联度的影响，分辨系数取0.5，将表1 中的数据代入式（3—5），得到压边力、冲压速度、模具间隙、摩擦因数1、摩擦因数2 等与最大减薄率的关联度分别为0.798 515，0.643 192，0.574 564，0.561 792，0.516 574。可知，模具间隙、2 个区域的摩擦因数关联度较压边力、冲压速度的小，则认为模具间隙、摩擦因数1、摩擦因数2 等3 个变量的影响均较小，其大小按生产标准进行赋值，模具间隙取1.1 倍料厚，即1.32 mm；摩擦因数分别为0.05（摩擦因数1）、0.2（摩擦因数1）。

2.1.2 拉丁超立方抽样

上述正交试验中的参数设定过于绝对，为了提升后续拟合及优化的准确性，采取拉丁超立方抽样法进行输入参数确定，对区间为[1.5 m/s,3.5 m/s]的冲压速度及区间为[1.372 MN,1.96 MN]的压边力进行随机取样，得到含量为50 的样本，其数据如图5 所示。

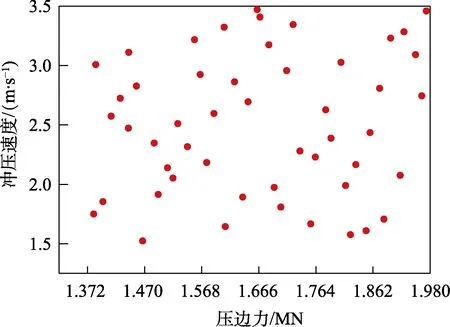
图5 拉丁超立方抽样数据Fig.5 Latin hypercube sampling data

2.2 神经网络拟合及遗传算法寻优

2.2.1 整体算法简介

文中利用神经网络遗传算法对深腔型零件冲压工艺参数进行寻优，其算法如图6 所示。

图6 整体算法流程Fig.6 Overall algorithm flow

将前文拉丁超立方获得的样本数据进行BP 神经网络训练，获得其BP 神经网络模型。另一方面，利用遗传算法获取不同变异状态下的设计变量X[x1,x2]，即冲压速度和压边力的组合，利用建立好的BP 神经网络进行预测，寻找该BP 神经网络模型下的最优输出参数y，即最大减薄率。

2.2.2 BP 神经网络建立

当前，BP 神经网络是研究和应用广泛的神经网络模型之一，其主要特点是向前传递信号，反向传递误差值，可实现输入到输出的任意非线性映射。其一般拓扑图如图7 所示。

图7 BP 神经网络拓扑图Fig.7 Topological graph of BP neural network

学习值是影响BP 神经网络训练速度及模型精度的主要因素之一，过大的学习值会导致训练速度过快，且引发系统不稳定；反之会导致收敛速度过慢，进而降低计算效率。文中将学习值设置为0.1[15—16]，并对上述优化模型进行拟合。

其中，隐层神经元个数由经验公式确定，如式（7）所示。

式中：l为隐层神经元个数；m为输入个数；n为输出个数；a为1 到10 的整数。代入得隐藏神经元个数的区间为[3,13]，文中该值为8。

2.2.3 拟合结果

在MATLAB 中建立结构形式为2-8-1 的BP 神经网络模型，其算法分别选取Scaled Conjugate Gradient，Bayesian Regularization 和Levenberg-Marquradt，其对应的均方误差分别为0.0298，0.0038，0.0066，回归值（R值）分别为0.676，0.98，0.97。

一般认为均方误差的值越小，R值越接近1，其训练效果越好，故文中选取Bayesian Regularization算法进行训练计算。选取上述50 组数据中的41 组作为训练数据，其余9 组作为测试数据，其预测输出与期望输出的分布如图8 所示。

由图8 可知，在BP 神经网络预测阶段，最大相对误差为4.8%，最小相对误差为0.1%，相对误差均小于5%，故该神经网络具有较高的预测精度。

图8 预测输出与期望输出Fig.8 Comparison of predicted output and expected output

2.2.4 遗传算法寻优

遗传算法是一种利用模拟生物进化过程求解复杂非线性优化问题的有效方法，即通过对参数进行杂交、繁殖、选择及竞争等操作，将其遗传算子代入算法中进行待解参数的寻优。

遗传算法主要包含遗传编码、个体适应度、选择阶段、交叉操作及变异操作等5 个部分。文中的遗传编码采取寻优能力较强的二进制编码，将最大减薄率作为适应度。种群规模大小为20，交叉概率为20%，变异概率为20%，迭代次数选取为100。经过迭代计算，最小适应度，即最大减薄率为16.47%，对应的变量为（1563.6,140.0），即冲压速度为1.5366 m/s，压边力为1.372 MN，如图9 所示。

图9 适应度曲线Fig.9 Fitness curve

2.3 有限元验证及零件试制验证

保持模具间隙及2 个区域的摩擦因数值不变，将上文获得的最优工艺参数输入到有限元模型，得到壁厚分布如图10 所示。

由图10 可知，最大减薄率为16.35%，与神经网络遗传算法预测结果相比，两者最大相对误差小于2%，满足生产制造要求。

图10 减薄云图Fig.10 Thinning contours

利用上文的最优工艺参数组合对该深腔型零件进行成果试制，如图11 所示。对其壁厚进行测量，最大减薄率为17.8%，发生在凹模圆角处，与BP 神经网络预测结果的误差小于6%，达到了工艺参数优化的目的。

图11 试验所得零件实物Fig.11 Physical parts obtained from test

3 结语

文中以优化某航空深腔型零件冲压工艺参数为目的，将GS 理论和神经网络遗传算法相结合，改善了该零件的冲压成形质量，获得以下结论。

1）文中利用正交试验法及GS 理论，确定了影响该零件冲压成形最大减薄率的2 个主要因素，即冲压速度和压边力。

2）文中建立了一种神经网络遗传算法，对压边力及冲压速度进行了参数优化。结果表明，在冲压速度为1.5366 m/s，压边力为1.372 MN 的条件下，其最大壁厚减薄率最小，为16.47%。

3）在上述研究基础上，进行了有限元及零件试制验证。结果表明，其验证的最大减薄率同预测值几乎相吻合，成形零件表面质量好，满足生产要求，验证了该方法的可行性。