古沙漠沙丘形态定量重建研究

马 静1,，曹 硕，张之辉，王成善

(1.中国冶金地质总局 矿产资源研究院，北京 100000； 2.中国地质大学(北京) 地球科学与资源学院，北京 100083)

沙丘形态学是认识和研究沙漠地貌的基础，近年来高分辨率卫星影像等技术的广泛应用大大推进了现代沙丘形态参数定量化的研究进程[1]，随着无人机技术的引入，古沙漠沙丘形态参数的测量具备了可操作性。目前，重建内部沉积架构和时空演化模型是古沙漠研究的重点内容[2]，但一直存在缺少定量数据约束其规模的问题，古沙丘形态参数定量化有望为恢复古沙漠沉积模型规模及识别高大沙山等特殊沉积单元提供有效支撑[3-4]。与较易获得替代性指标的古风向重建相比[5]，古风力研究相对薄弱，是古风场乃至古气候重建研究的难点之一[6]，古沙丘作为古风场的直接地质记录，其形态参数定量数据是恢复古风力条件的良好指征。因此古沙丘形态参数研究，符合当前地球科学研究的需要，有助于古地理及古环境的重建。古沙漠是干旱气候条件的灵敏指针，其内部古沙丘的形态受到古风场、古地形的直接控制，对古沙漠沙丘形态参数的定量重建，有助于重建古风场并约束古地形展布，具有重要的古地理及古气候意义，同时也可对未来沙漠的演化提供重要参考，以期为古沙丘形态参数定量重建提供有效的方法学支撑。

“将今论古”是研究深时地球强有力的工具，定量重建古沙丘形态需依靠现代沙漠沙丘形态学。虽然通过现代沙漠开展的大量沙丘形态学研究，已基本明确沙丘形态参数测量及评价的指标体系，但由于不同因素的差异影响，导致不同沙漠沙丘形态参数之间的换算关系存在较大差异性[7-8]，这大大增加了建立古沙丘形态参数定量恢复方法学的难度。因此，对沙丘形态参数及其换算关系开展系统的方法学研究极为重要。本研究通过综述大量现代地貌学对沙丘形态的研究，在前人研究基础上总结沙丘形态参数函数关系，探讨形态参数换算公式差异性的影响因素，结合古沙漠沙丘沉积特征和演化规律，建立古沙丘形态参数测量和计算方案，为构建古沙漠沉积模型、沉积机制以及重建其古地理古环境提供借鉴，并为定量恢复古风场等古气候研究奠定基础。

1 沙丘形态学分析方法

1.1 沙丘形态描述(形态参数)

早期风沙地貌学家通过对沙丘开展基础形态描述和水槽模拟实验，形成了大量沙丘基本形态的重要理论[9-13](表1)，遵循描绘客观详细和便于在遥感影像上量测的基本原则，沙丘形态基本参数包括：高度、波长、宽度、间距、横截面面积、脊线轴长与轴向等[11，14](图1)。

表1 沙丘形态参数表

1.2 古沙丘形态参数体系

沙丘经过迁移堆积固结成岩形成的沉积亚相主要包括沙丘相和丘间相。沙丘相按规模可进一步划分为简单型沙丘和复合型沙丘群[15-16](图2)。简单型沙丘为独立沙丘形成的中厚层砂岩层，其上下可能夹有丘间、沙席沉积，沙漠边缘到中心地区均有分布。复合型沙丘群由大型沙丘群组成，只在沙漠中心地区发育。在平行于主风向的剖面中，沙丘相内部发育大型板、楔状交错层理(图3)；在垂直于主风向的剖面上，可见大型连续槽状交错层系组[11]。丘间相根据沉积过程干湿状态可分为干丘间和湿丘间，干丘间为薄层或透镜状砂岩，发育平行状层理；湿丘间沉积则一般具有水成沉积特征，为泥质-细粉砂岩，具粒序、水平或波状层理，呈层状发育在沙漠边缘[17]。

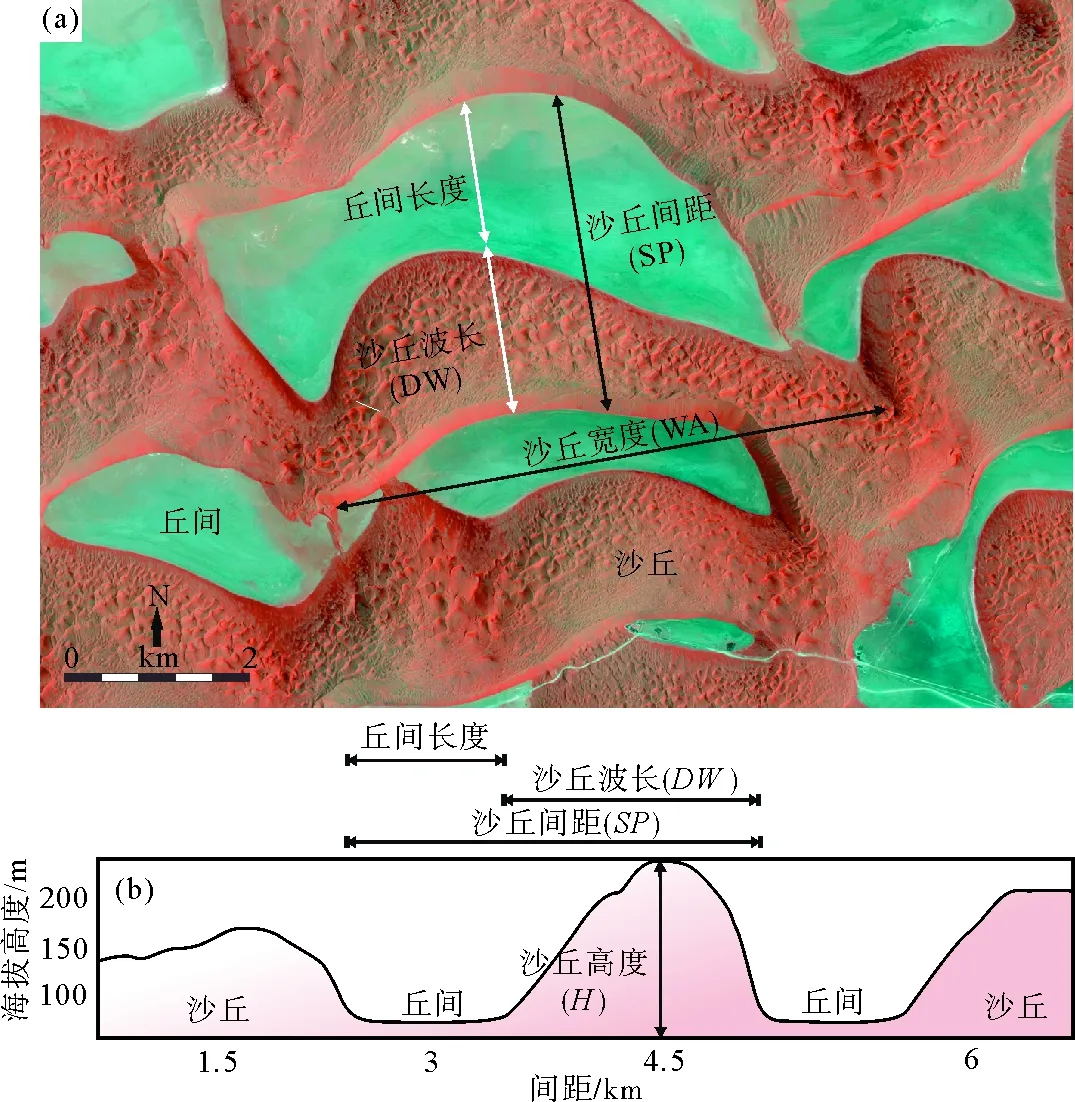
(a)平面卫星影像图;(b)切面示意图

古沙漠沉积体系内部发育有不同级别的风成界面[18]，根据沙丘底形迁移形式可分为再活化界面(reactivation surface，简称R)、叠置界面(superimposition surface，简称S)、丘间迁移界面(interdune migration surface，简称I)和超界面(supersurface，简称SS)(图2)。再活化界面(R)是由风向等变化引起底形迁移改变形成的阶段性再沉积；叠置界面(S)形成于大型底形之上小型沙丘的叠置迁移，以板状、大型扇状侵蚀面为特征，倾向变化较大[19]；丘间迁移界面(I)形成于沙丘与丘间沉积之间，以板状或微扇状展布，倾角较小延伸较长；超界面(SS)代表着相变或沉积间断，其形成与发育可作为沉积层序的分界，可延伸几百至上千米[20]。

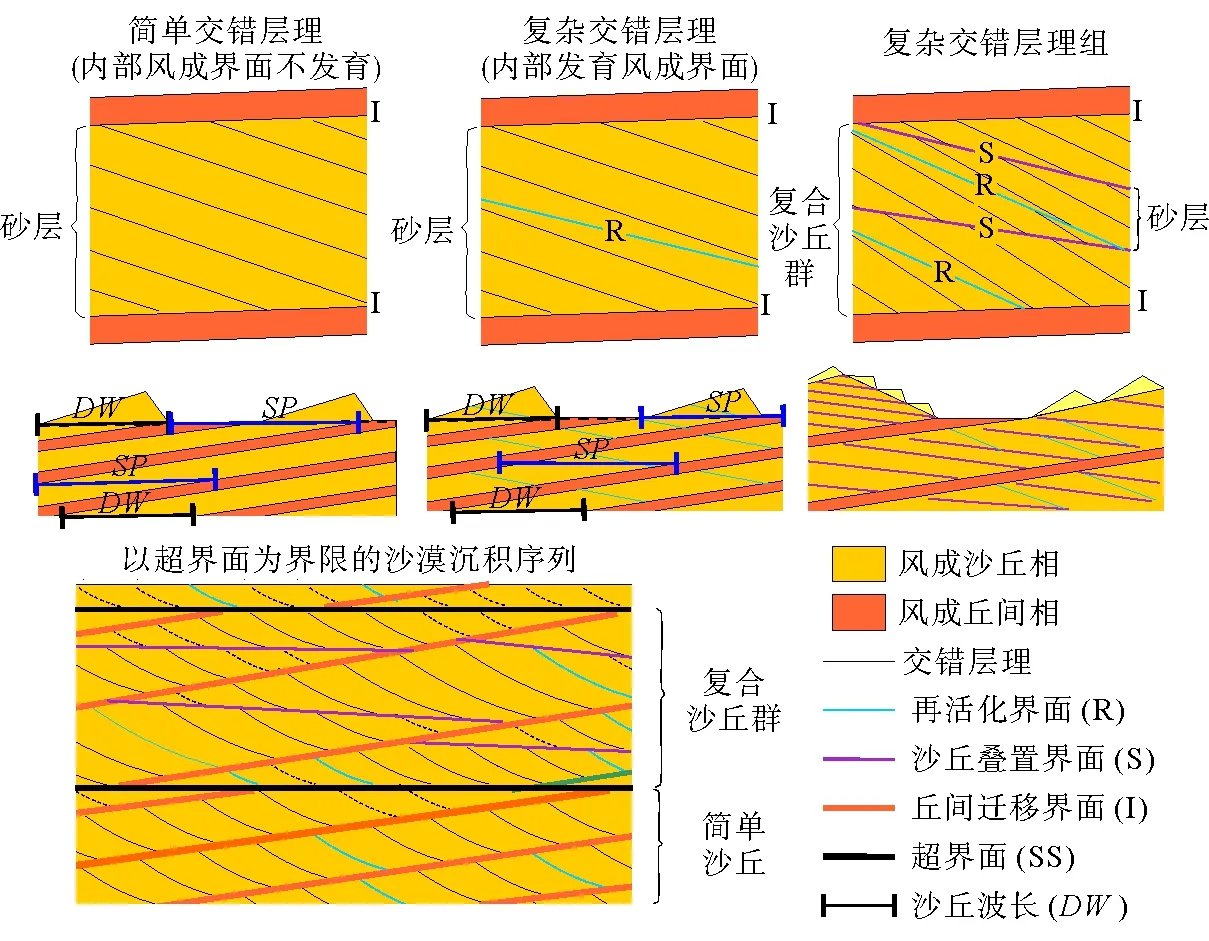
图2 古沙漠沉积系统沉积界面几何学模型(修改自Kocurek等[15]、Mountney[16])

在沙丘迁移堆积固结成岩过程中，通常只有沙丘的下半部分可以保存下来，沙丘的上部(90%或更多)被上覆沙丘推进截断[21]，大部分原始沙丘沉积物被剥蚀(图3)，因此古沙丘沉积并不能反映沙丘的原始形态。本研究借鉴近年来现代沙丘形态参数体系，结合古沙丘迁移、叠置、固结成岩的特点，选取古沙丘形态参数识别及测量方法如下：

1) 古沙丘高度(H)：古沙丘顶最高点至底部的垂直高程，远大于地质记录中岩层厚度。

2) 古沙丘波长(DW)：古沙丘底面在垂直于沙脊线上的延伸，根据古沙丘沉积机制，在地层记录中，通过测量超界面(SS)或与之平行的表面上沙丘连续迁移爬升的点之间的顺风距离，即可得到原始波长[16,18](图3)。

3) 古沙丘间距(SP)：古沙丘迎风坡坡脚到紧邻沙丘迎风坡坡脚的水平距离，剖面超界面或与之平行的表面上连续丘间迁移点之间的顺风距离[11](图3)。为波长与丘间顺风方向长度之和，在沙漠中心相，丘间沉积几乎不发育，沙丘间距与沙丘波长近乎相等(图1)。

4) 古沙丘宽度(WA)：指古沙丘两翼端点间的水平距离，通过在垂直于主风向的剖面上测量槽状层理两翼角之间的最大距离得到(图2)。古沙丘翼角部分可根据出露情况进行数据可信度分类。

5) 粒流层平均厚度(t)：粒流层(grainflow strata)是指由于重力作用，背风坡表面砂体发生崩塌，砂粒沿滑落面向下滑落沉积形成的层理[22]。在现代沙漠中通常为背风坡表面砂粒的流动轨迹，在地质剖面中常与粒落层(grainfall laminae)、沙波层(ripplecross-strata)交替沉积组成沙丘前积层(图4)， 内部微逆粒序且呈舌状延伸[23]。实测需选择垂直或平行于古风向的地质剖面，避免测量粒流层斜截面使测量值偏大[19]。为保证数据测量具备统计学意义，对单一粒流层厚度的测量次数应多于100次并取平均值。

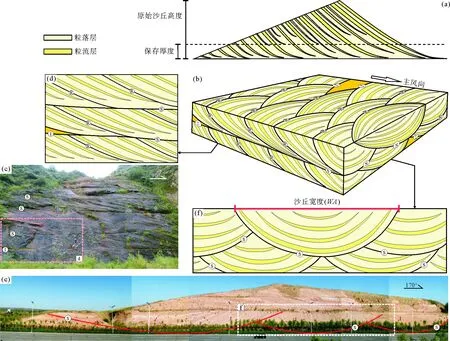
(a)古沙丘保存层厚与沙丘高度关系图；(b)沙丘相与丘间相沉积架构模式图；(c)平行风向露头剖面；(d)平行风向剖面架构示意图；(e)垂直风向露头剖面；(f)垂直风向剖面架构示意图

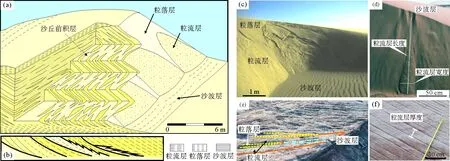
(a)沙丘背风坡前积层层理结构示意图；(b)沙丘底部横切面层理结构示意图；(c)现代沙丘背风面；(d)现代沙丘粒流层形态参数；(e)古沙丘沉积粒流层；(f)沙丘沉积粒流层形态参数

6) 岩层厚度(λ)：大型复合沙丘群组中边界面(I)圈定出的单层沙丘层的垂直高度，可间接计算出沙丘的原始波长(图5)。

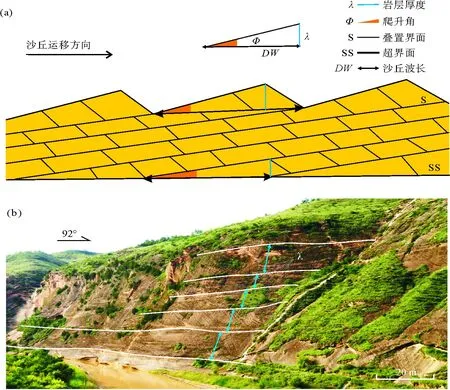
(a)底形爬升模型示意图；(b)鄂尔多斯盆地白垩纪洛河组洛河剖面复合古沙丘群组形态参数

7) 爬升角度(Φ)：复合型沙丘群组中边界面(I)平面上沿古风向爬升[21]，与超界面之间存在的倾角差即为底形(bedform)的爬升角度。

2 沙丘形态参数定量计算方法

根据现代沙丘形态的大量实测及水槽模拟实验数据，发现尽管不同沙漠中沙丘的类型、规模有差异，但大多数沙丘的形态存在普遍规律，同时各形态参数之间具有良好的相关性[22-23]。

新月形、类新月形沙丘作为沙漠中最基础的沙丘类型，分布广泛且结构简单，在长距离顺风迁移的过程中为封闭系统，不会经历大小或形状的重大变化[24]，且可组合成多种类型沙丘群[25]，因此常被作为典型的风沙地貌体来研究其形态变化及移动规律。在地层记录中新月形、类新月形沙丘在沙漠中心、边缘相均有发育，形成厚层沉积记录，表示风场或供沙环境单一稳定[12]。对沙丘形态特征的分析，有助于揭示沙丘形成发展的一般规律，为解决其他复杂类型的巨大沙丘提供参考，故本研究以新月形、类新月形沙丘为典型古沙丘类型为主来研究其形态参数规律。

2.1 沙丘高度与间距(H-SP)

沙丘高度和间距之间具有良好的相关性(表2)。Lancaster[29]通过对纳米比亚沙漠沙丘的野外测量，结合已有的同类数据，提出可以用幂函数来表示沙丘高度和间距之间的关系，指数为0.52～1.72；Blumberg[27]通过SRTM方法估算出纳米比亚沙漠、墨西哥Gran沙漠中沙丘高度和间距之间关系式为H=0.058SP0.90。我国大型沙漠中沙丘也表现出类似的关系，哈斯[28]测量了腾格里沙漠东南缘的沙丘形态,得到其幂指数为0.86～1.68；Dong等[3]通过对巴丹吉林沙漠东南部高大沙山形态研究，结合前人结论进一步归纳得出沙丘高度和间距之间的关系为H=0.12SP；宁文晓等[7]对巴丹吉林沙漠同区域开展沙丘形态学研究发现，沙丘间距每增加1 m，沙丘高度就会升高55 m；白旸[4]通过对巴丹吉林沙漠高大沙山数据进一步拟合，得出高大沙山沙丘高度与间距间关系为H=0.08SP1.01，小型沙丘、沙波纹层高度和间距之间的关系为H=0.12SP0.8；汪克奇等[8]基于DEM方法对巴丹吉林沙漠6 033个独立沙丘进行形态学研究，发现各类沙丘的沙丘间距与沙丘高度均表现为线性正相关关系。

表2 全球不同沙漠沙丘高度-间距关系表

综上，不同类型的沙丘高度与间距之间存在相关关系，可用幂函数H=a×SPb(a、b为自然数)表示，同时由于沙丘所处位置、大小等属性不同，公式系数存在一定差异。

2.2 沙丘宽度与高度(WA-H)

根据地貌动力学研究结果，沙丘宽度与高度的关系受休止角控制，向沙丘顶部添加颗粒将自动导致沙丘加宽，两者之间存在线性关系[30](图6)。

Finkel[31]测量了秘鲁南部高度<6 m的新月形沙丘的形态参数，得出WA=10.3H+4；Hastenrat[34]分析了同一地区的沙丘，得出WA=8.19H+9.52；Mabbutt[34]分析得到WA=9.58H+5.75，并且发现全球沙漠新月形沙丘的高度约为沙丘宽度的十分之一；Hesp等[30]根据秘鲁南部、纳米比亚沙漠的数据，得出WA=8.82H+7.65，加上加利福尼亚帝王谷数据，得出WA=18.37H-15.77[33]。李志忠等[35]在塔里木沙漠石油公路沿线的测量结果表明，新月形沙丘最大高度多为其两翼宽度的1/10；Wang等[36]在民勤绿洲观测表明沙丘高度与宽度呈正比例关系，比例系数为15.61；任孝宗等[37]对巴丹吉林、腾格里沙漠沙丘形态测量，得出比例系数为15.14，库姆塔格沙漠比例系数为11.29；郭建英等[38]对乌兰布和沙漠实测，发现沙丘高度与宽度关系式为WA=16.7H-58.5；刘宇胜等[39]发现阿拉善戈壁地区新月型沙丘形态存在WA=22.617H-17.106的关系。

因此，沙丘宽度与高度的关系可以用WA=a×H+b(a、b为自然数)表示(表3)，系数的不同，可能是由于沙丘未达到平衡高度(即稳定状态)、坡度角未达到休止角[27]等原因。

2.3 粒流层厚度与沙丘高度(t-H)

随着沙丘高度增加，沙流中携沙量增加，粒流层沉积也会随着斜坡长度的增加而变厚[19]，但这种关系仅应用在粒流层到达底部的中小型沙丘中[12]。Hunter[40]通过美国Entrada砂岩研究发现，单个沙丘中的粒流层厚度随沙丘高度以非严格线性方式增加；Kocurek等[12]通过对其数据进一步校正拟合，得到H与t之间的关系式：H=988.78t1.479 6；Romain等[13]通过对雪松台地砂岩和纳瓦霍砂岩研究发现，H与t之间存在关系H=1 532.7t1.600 6。

因此，中小型古沙丘的粒流层厚度与沙丘高度之间存在相关关系式，可用幂函数H=a×tb(a、b为自然数)表示，参数之间存在差异，可能与沙丘规模有关[13](图7)。

2.4 岩层厚度、爬升角度与沙丘波长(λ,Φ-DW)

对于风成岩层的成岩机制，目前底形爬升机制仍是最有力的解释[41]。根据底形爬升机制理论，在泥沙供应和风力条件下，形成不同规模底形(bedform)[16]，风积作用强，堆积面上升时，底形相对于沉积表面向上移动(爬升)，随着潜水面垂直上升，砂粒吸水固结并逐步形成地层，最终形成岩石记录[18]。由底形爬升而形成的沙丘岩层，其层厚和原始床身波长及沉积过程中的爬升角度具备三角函数关系：DW=λ×cotΦ[11](图5)。

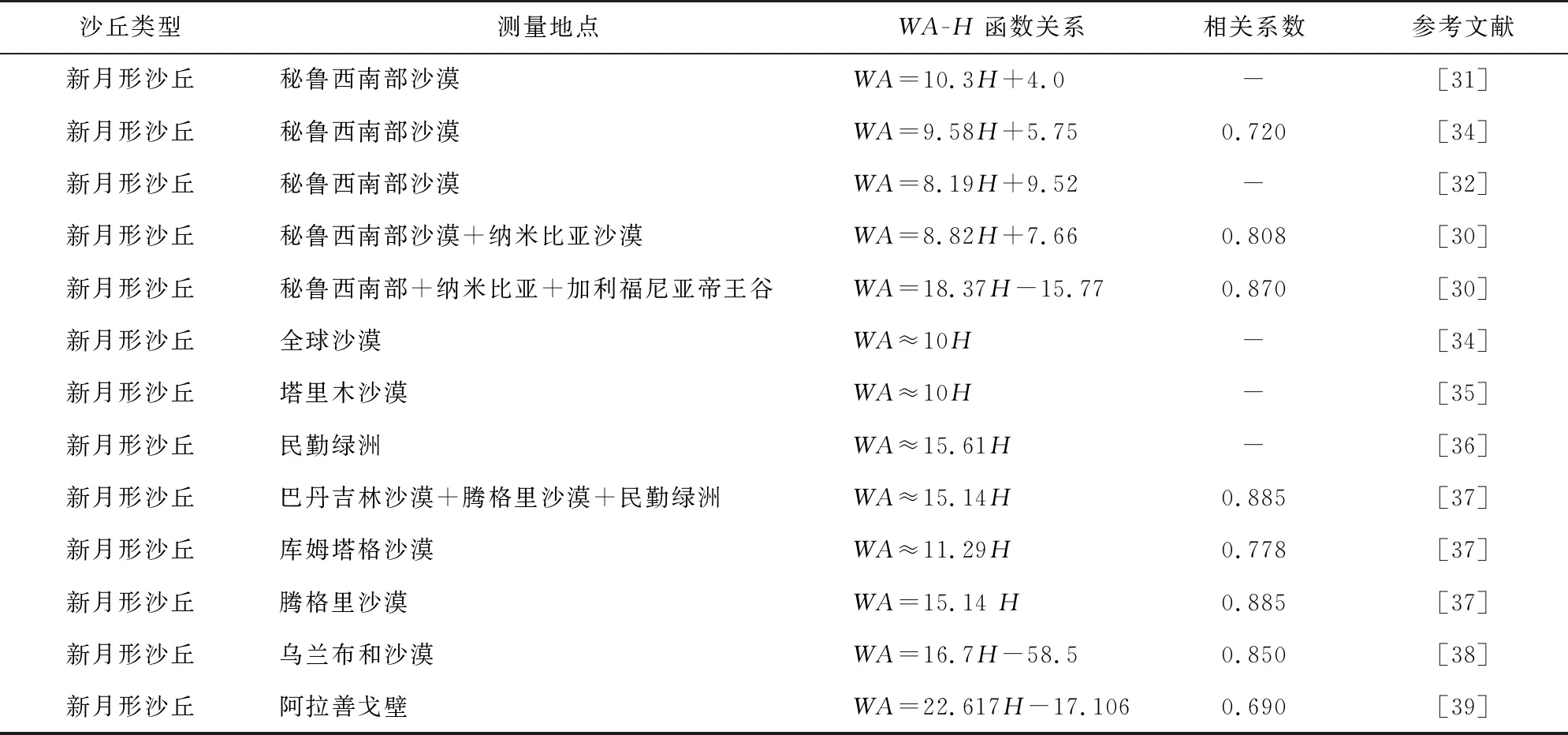
表3 全球不同沙漠沙丘高度-间距关系表

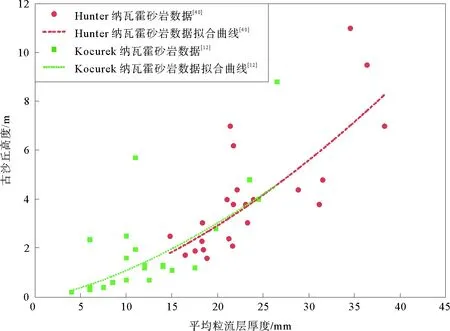
图7 纳瓦霍砂岩和现代撒哈拉沙丘粒流层厚度-高度关系比较(引自Romain等[13])

2.5 沙丘高度及对比性分析

对于古沙漠的规模及其内部变化规律一直缺乏深入的研究。沙漠体系从边缘到中心环境沙丘具有怎样的演化规律?在时间和空间尺度上，如何对比不同地质时期或是同一时期不同地点沙漠的规模?地质历史中特殊的温室气候阶段以及未来的温室地球，沙漠具有怎样的演化特征？为解决这一系列的科学问题，需选定具有可对比性并可测量、计算的沙丘形态指标。

对于现代沙漠，借助遥感影像和数字高程图像等软件的空间分析功能，前人统计分析了现代不同沙漠中沙丘形态参数在沙漠中心和边缘之间的差异，其中高度作为沙丘形态最直观的指标，常用来对比分析整个沙漠的沙丘空间布局，进而分析该沙漠沉积体系的物源供给、风力状态等[1]。不同沙漠间的沙丘高度存在差异，纳米比亚沙丘高度通常分布在20～50 m，美国Algodones沙丘高度多为50～80 m[10]，我国巴丹吉林沙漠的东南部高大沙丘密集分布，沙丘高度多分布在200～450 m[7]。这种差异可能与沙漠地形、风场、规模有关[28]，故沙丘高度是反映沙丘规模、形成时间和动态变化的重要指标，可作为重要的对比参数来反映沙丘宏观形态以及沙漠中不同沙丘的空间分布。

古沙丘形态参数体系中，沙丘原始高度(H)也可作为对比指标反映沙丘空间组合趋势，进而恢复当时沉积环境动力学过程。但岩层中保留的沙丘层厚并不能代替沙丘原始高度，沙丘高度无法直接测得。通过对上述形态参数关系式的统计分析发现，沙丘间距、波长、宽度、粒流层厚度等要素均可与沙丘原始高度建立相应函数关系。可通过实测参数加上相关关系式计算，最终恢复古沙丘的原始高度(H)。

3 古沙丘形态参数定量重建

3.1 沙丘形态参数换算公式差异性的影响因素

不同沙漠中沙丘形态参数换算公式系数存在明显的区别，即使是同一沙漠空间内相邻的沙丘之间参数关系也存在些许差异[10]，这可能是受内外部因素共同影响的结果，主要包括砂粒性质、地表形态、风力性质和植被覆盖等。

1) 砂粒性质：主要包括砂粒的粒度和分选性。全球不同沙漠沙丘砂粒性质存在差异，在墨西哥Grand、印度Thar、澳大利亚Simpson 和西班牙Gran沙漠中的沙丘砂粒粒度细(150～180 μm)，分选好；Namib和撒哈拉西北部沙漠的沙丘砂粒粒度中等(200～240 μm)，分选一般，粗砂出现在海岸沙丘；美国Kelso、Algodones沙漠和西班牙Gran沙漠北缘，分选较差[42]。风力对大量砂粒的携带从有限到大规模的级联跃迁的转变可以在非常小的风速范围内发生，这种转变值即为有效风力临界值，砂粒的大小、分选通过影响该转变值进而对沙丘形态的塑造进行干扰[43]。一些学者也通过模拟实验证实了砂粒性质与沙丘形态的关系，Lancaster[29]和Tsoar[44]研究表明，砂粒较粗时，沙丘底部和顶部之间的输沙率差异可能很大，砂粒搬运集中在顶部，因此沙丘形态倾向于平坦，具有较低的宽高比。Hersen等[45]也通过不同粒度的砂粒形成沙丘的模拟实验发现，砂粒粒度较细、分选较好时，沙丘坡度更陡，粗沙较多时，新月形沙丘的坡度较平缓。

2) 地表形态：主要包括地表的粗糙度以及地形起伏。在不同基底下，例如粗糙的石质地面和光滑的盐田之间发育的新月形沙丘形态存在明显差异[42]。Kocurek等[15]记录了德克萨斯州Padre岛沙丘的形成和生长，由于地形的微变化，风速降低从而形成波纹。随着沙子供应量增大，一些波纹发展成沙丘。在波纹形成沙丘过程中，并不是所有的波纹都以相同的速度发展，许多小的波纹甚至消失，这种发展模式与地表形态密切相关。地表的粗糙度影响着有效风力临界值，随着粗糙度的增加，施加在风上的表面阻力也增加[46]。低风速下，只能在较光滑的表面上输砂；中等风速下，较光滑的表面上输砂量大；高风速下，粗糙表面上的输砂量反超，沙丘的增长受到正反馈，高宽比增加[42]。

3) 风力性质：主要包括风向和风速[47]。沙丘形态是迎风坡侵蚀和背风坡沉积作用的产物。在沙丘迎风坡，风力加速，使顶部的泥沙通量增加和泥沙的净侵蚀；在沙丘背风坡气流通常是复杂的，一般发生砂粒沉积和沿坡砂粒的流动。风力的大小与方向变化影响着泥沙输移速率的空间变化，风力大小影响着沙丘的坡度、高宽比，在低风速时期，沙丘的坡度更陡，随着风速的增加，沙丘宽度增加，整体形态愈加圆润[48]。在风向变化的地区，风向改变着侵蚀和沉积的空间格局，沙丘形态也向着新的平衡方向调整。

4) 植被覆盖：植被配置结构和生长特征、高度等会对沙丘形状产生一定影响[12]。植被覆盖的沙丘形态要素的比例关系主要取决于植被的性质和随后由于风力作用冲刷而形成的状态[10]。被匍匐茎植被覆盖的沙丘，一般两翼之间较宽阔、高度较低，常见于海洋沿岸；被草丛(如冰草、披碱草等)覆盖的沙丘，一般垂直高度较高、坡脚较陡，常见于温带内陆盆地[42]。Kocurek等[12]利用在羊茅等植物覆盖型金字塔形沙丘的形成模拟实验，证明沙丘的高度主要由植物的宽度和沙的休止角决定。植物底部越宽，在达到休止角之前可以建造的沙丘高度就越高。

3.2 古沙丘形态参数函数关系选择方法

由于现代沙漠中沙丘的砂粒性质、地表形态、风力状况、植被覆盖情况等因素存在差异，导致不同沙丘形态参数之间换算公式系数不同，部分拟合曲线相关系数较低，统计学意义较弱，因此在选择公式进行古沙丘形态参数定量计算时存在一定困难。

砂粒的粒度和分选性影响着沙丘形态参数换算公式的系数。在利用野外实测数据计算恢复古沙丘其余形态参数时，应对岩石样品进行粒度分析，与可选公式区域内砂粒性质进行对比，选择相似程度高的公式进行计算可转大程度地规避砂粒性质对形态产生的影响。

地表的粗糙度、地形起伏通过影响有效风力临界值、输沙率的空间变化等影响沙丘的形状。而古沙漠露头大多形成于大型盆地内，古沙丘均沉积在沙覆盖或半覆盖的表面，由于输砂量高使沙丘底形不断爬升、叠置，最终固结成岩。所以地表形态对换算公式的选择影响不大。

风力的大小与方向变化影响着沙丘的坡度、高宽比。古风场的恢复目前主要根据沙丘前积层倾角利用玫瑰花图来重建。但古沙漠形成地层记录需要相当长的时间，在沙漠中心相风力状况较为规律，偶然间的风场改变几乎没有。所以可根据获得的大部分风力状况数据对古沙丘形态参数换算公式进行选择，力求公式数据所在的现代沙漠与古沙漠基本风向一致，风力类似。

植被对沙丘形态产生影响。古沙漠中植被的发育情况可以根据沉积相地层序列及平面展布进行分析，例如：沙漠相上下地层出现湖泊、沼泽等水成相，则代表植物比较发育。一般古沙漠中心地区植物鲜少发育，在边缘相地区偶尔出现，在地层中表现为遗留古生物化石或者岩石颜色较黑，有机质含量较高等。可根据地层序列中沉积相组合及特殊岩性特征来推测植被情况，选择与植被发育情况类似的现代沙漠的沙丘形态参数公式来规避植被的影响。

综上，在定量恢复古沙漠中古沙丘形态参数时，为提高计算结果的准确性，应结合粒度分析实验、古风场等数据结果，选择条件相似的现代沙漠的形态参数公式，最大限度地减小影响因素的差异性。另外，由于研究程度的加深和技术手段的改进，现代沙漠数据的不断更新充实，在运用公式时应进一步整理统计、筛选分析，并再次计算拟合获取更准确的现代沙漠形态参数公式。并对计算出的古沙漠形态参数进行验证，通过同一层风成岩层的多个形态参数的测量，根据相应参数公式计算得到两个高度(H)数据进行对比，若差别不大，即可保证公式选择与古沙漠形态恢复的准确性。

3.3 研究不足与展望

本研究依据现代沙漠沙丘形态参数及其对应换算关系，定量重建古沙丘形态参数体系，补充古沙丘形态参数测量及定量计算方法的空缺，有望为恢复古沙漠沉积模型规模及识别高大沙山等特殊沉积单元提供有效支撑，为探究古沙漠沉积机制提供新的研究思路，但仍存在以下不足：

1) 沙丘形态参数计算方法尚不成熟。虽然前人对现代沙丘形态学已经开展了理论研究和参数计算，但不同地区或不同类型的沙丘形态参数之间的函数关系仍存在明显差异性[4,7-8]，缺少形态参数之间的通用换算公式，亦或是不同系数的函数公式应用范围不明确，增加了开展古沙丘形态定量重建的难度。

2) 古沙丘出露完整性不足以及实测难度较大。由于古沙丘经历了沉积叠置、截切风化等多阶段作用，多数保存不完整[21]，因此实测数据往往小于沙丘原始数值；另外，一些保存完好的古沙丘露头规模较大或出露位置陡峭，人力较难完成实测。

3) 对古沙丘形态学研究的古地理及古气候意义挖掘不足。对地质历史时期中的古沙丘形态参数的定量重建，为重建古大气环流模式提供了直接的地质证据[17]，地质历史特殊气候时期古沙丘的形态学研究可为未来沙丘的演化提供借鉴。古沙丘的发育不仅受气候控制，还与山脉、峡谷等地形条件紧密相关，对沙丘形态演化及分布规律的研究有助于重建古地理格局[12,16]。

4) 缺少古沙丘形态学研究实例。实例应用是检验理论分析最好的方法，随着对古沙漠等风成沉积记录识别的不断完善，为古沙丘形态学研究的开展提供了很好的素材。古沙丘形态参数定量重建实例研究不仅有助于完善古沙丘沉积及演化规律，还可以验证及修正现有形态参数函数关系的正确性和相关应用条件，同时提供有效数据支撑。

尽管目前古沙丘形态学研究及定量形态参数重建存在以上诸多不足，但随着研究方法及技术的改进和数据量的不断强化，对现代沙丘和古沙丘形态学的研究进行展望。

1) 优化数据统计及分析方法。借助大数据平台，进一步分区、分类型统计现代大中小型沙漠中心、边缘地区的可测沙丘形态参数，借助数据分析软件进行公式拟合，以期得出更准确的形态参数通用计算公式。

2) 提高沙丘形态参数野外数据实测的准确性和全面性。受限于人力测量的操作难度，大量沙丘形态参数未开展实测或测量数据准确度不足，通过引入无人机倾斜摄影技术，可以大大增加沙丘形态参数实测的准确度和数据量。

3) 选定典型古沙漠开展古沙丘形态参数定量重建，并探究其古地理及古气候意义。由于古沙丘形态重建的难度远大于现代沙丘，因此对出露条件的要求较高，早白垩世鄂尔多斯盆地发育典型的大型沙漠沉积，具备分布范围广、地层连续性高、出露完整且沉积特征典型等特点[49]，为开展古沙丘形态参数重建提供了绝佳素材，可为后续古沙丘形态学研究建立模板。另外，由于早白垩世是地质历史中典型的温室时期，对该时期古沙漠沙丘形态参数定量重建，具有重要的古地理及古气候意义，同时也可为未来温室地球沙漠演化提供重要参考[17]。

4 结论

现代沙丘形态参数体系的建立是沙丘形态学研究的重要突破，为古沙丘形态学研究特别是形态参数定量重建提供重要的方法学支撑。定量重建古沙丘的形态参数为古沙漠时空演化模型的构建提供定量约束，有利于恢复其沉积环境动力学过程，为探究古沙漠沉积机制及其古气候和古地理意义提供了新的研究思路。

本研究依据“将今论古”思想，借助现代沙漠沙丘形态学研究方法，引入现代沙丘形态参数：沙丘波长(DW)、沙丘间距(SP)、沙丘宽度(WA)、沙丘高度(H)，结合古沙丘沉积特征，补充参数：层厚(λ)、爬升角度(Φ)和粒流层厚度(t)，最终建立古沙丘形态参数体系。阐述大量前人关于沙丘形态参数数据及函数换算关系，最终选定沙丘高度(H)作为沙丘形态的统一对比指标。并总结函数关系差异性的影响因素，主要包括砂粒性质、地表形态、风力性质和植被覆盖等。提出在重建古沙丘形态方法时，应综合考虑上述影响因素，以实测数据为基础，选择与古沙丘发育区条件相似的区域，依据该区域公式定量重建，最大限度地缩小影响因素造成的重建误差，并对计算结果进行数据对比验证，进一步提高公式选择的准确性。