裂隙岩体几何和力学表征单元体尺寸的颗粒流分析

李克利1，宋晓康，张昌锁

(1. 河南无线电管理信息系统备份中心，河南 郑州 450000；2.太原理工大学 矿业工程学院，山西 太原 030024)

关健词：颗粒离散元方法；裂隙岩体；尺寸效应；表征单元体；等效岩体模型

裂隙岩体是由完整岩块和结构面共同构成的复杂地质体，其强度和变形特性受到完整岩块和结构面的力学性质、结构面的几何分布特征以及岩体的应力状态等因素的影响[1]。由于错综复杂的结构面的存在，岩体在结构特征方面表现出非均质性和不连续性，导致岩体几何和力学参数方面表现出明显的尺寸效应。

表征单元体(representative elementary volume，REV)是确定岩体等效参数及选取岩体力学分析模型的基础[2]。在同一岩体结构统计均质区内，当岩体尺寸较小时，其中的裂隙分布会有较大的差异，因而岩体性质会有明显的波动性，随着岩体尺寸的增加，这种差异性会逐渐减弱，当岩体尺寸大于某一临界值时，岩体性质不再随岩体尺寸的增大而改变，这一临界值被称为REV尺寸。许多学者从岩体的几何参数和力学参数的角度出发，采用不同的方法研究岩体的尺寸效应，从而确定裂隙岩体的REV尺寸。根据分析参数的不同，岩体REV可分为几何REV、力学REV等[3]。几何REV方面，张贵科等[4]提出以单位体积内结构面在某截面上的投影面积作为岩体REV的衡量指标；王晓明等[5]、宋盛渊[6]从三维裂隙连通率的角度出发，确定岩体的REV尺寸；夏露等[7]采用块体百分比对岩体REV的存在及大小进行了分析；卢波等[8]通过分析岩体分形维数的尺寸效应来确定岩体REV尺寸；王晓卿[9]以裂隙密度参数P31(单位体积岩体内的裂隙数量)和P32(单位体积岩体内的裂隙面积)为指标来确定煤体REV尺寸；Oda[10]通过研究裂隙张量的尺寸效应来确定岩体REV尺寸； Li等[11]根据裂隙连通性参数C1(单位体积岩体内的裂隙交线数量)和L1(单位体积岩体内的裂隙交线长度)来确定岩体REV尺寸。力学REV方面，朱万成等[12]通过数值试验分析裂隙岩体的弹性模量、抗压强度和抗拉强度的尺寸效应，并据此来确定岩体REV尺寸；吴琼[13]通过计算裂隙岩体模型的抗压强度、变形模量、剪切模量、体积模量、泊松比随尺寸的变化规律来确定岩体REV尺寸；张婷婷[14]通过开展不同围压下的双轴压缩数值试验，分析弹性模量、泊松比、内摩擦角及黏聚力的尺寸效应来确定岩体REV尺寸；马超锋等[15]研究了三轴抗压强度随岩体尺寸的变化规律，分析三轴压缩状态下的岩体REV尺寸；王培涛[16]基于弹性模量、单轴抗压强度及裂纹起裂应力分析岩体的尺寸效应，最终来确定岩体REV尺寸。

现有关于裂隙岩体表征单元体的研究大多从几何参数或力学参数单方面来进行，对于几何REV和力学REV尺寸之间的关联性研究还相对较少。本研究在构建三维裂隙网络的基础上，以裂隙密度参数P32和P31为指标，确定岩体的几何REV尺寸，并通过对不同尺寸的等效岩体模型开展单轴压缩试验，以单轴抗压强度和弹性模量为指标，确定岩体的力学REV尺寸，对几何和力学REV尺寸的计算结果进行比较，分析两者之间的关联性。

1 几何REV尺寸的确定

1.1 裂隙地质参数

研究采用的裂隙地质参数来源于加拿大Brockville铁路隧道的测量数据，该隧道位于加拿大安大略省，是加拿大最古老的铁路隧道，全长520 m，现场测量数据使用激光扫描技术得到，经过概率统计分析及偏差校正，获得三维裂隙网络所需的输入参数，包括形状、位置、产状、尺寸及密度等[17]。该区域裂隙主要划分为3组，裂隙的形状假设为圆盘，裂隙的位置在空间均匀分布。表1为裂隙产状数据，裂隙的产状服从Fisher分布，Fisher常数K用于描述每个裂隙组产状的离散程度。表2为裂隙直径及密度数据，其中设定裂隙的直径在直径范围内服从幂律分布，幂律分布指数用于描述每个裂隙组直径的分布情况，裂隙的密度用P32来表征。

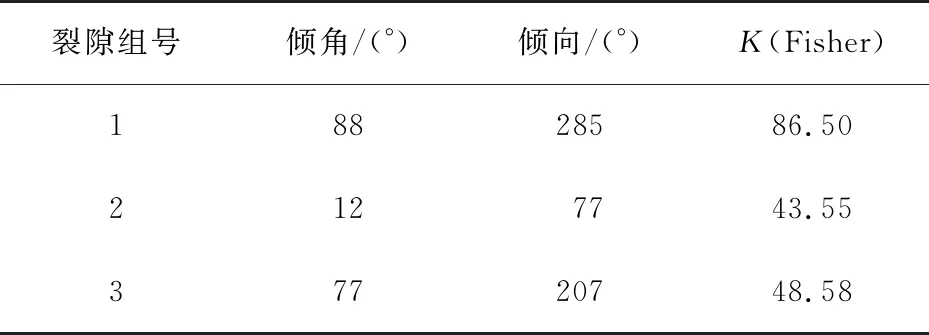
表1 裂隙产状参数Tab. 1 Fracture orientation parameters

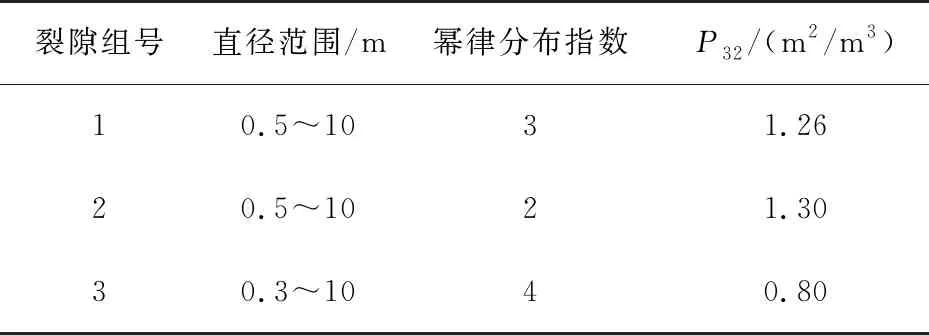
表2 裂隙直径及密度参数Tab. 2 Fracture diameter and density parameters

图1 三维裂隙网络1Fig. 1 Three dimensional fracture network 1

1.2 不同尺寸的裂隙网络模型

利用颗粒流软件PFC3D内置的DFN模块，根据裂隙地质参数及统计分布规律，采用Monte-Carlo随机模拟方法生成符合相应分布特征的随机数，建立40 m×40 m×40 m的随机三维裂隙网络模型，其裂隙分布情况与实际工程具有相似的统计分布特征。为了减小三维裂隙网络生成过程中产生的随机性误差，本研究生成了5个相同尺寸的三维裂隙网络，并将其作为母体从中切割出不同尺寸的裂隙网络模型，如图1所示为三维裂隙网络1。

从每个三维裂隙网络模型的中心依次截取12个不同尺寸的同心长方体模型，高宽比为2，宽度分别为0.05、0.1、0.2、0.5、1.0、1.5、2.0、3.0、4.0、5.0、6.0和7.0 m，共生成60个长方体裂隙网络模型。以其中一个三维裂隙网络为例，从中截取得到的不同尺寸裂隙网络模型如图2所示。可以观察到，随着裂隙网络模型尺寸的增大，截取到的裂隙数量在不断增多，有的裂隙会完全包含在裂隙网络模型中，而有的裂隙会被模型边界截断。

图2 不同尺寸的裂隙网络模型Fig. 2 Fracture network models of different sizes

1.3 几何REV尺寸

在裂隙岩体的几何参数方面，裂隙密度指标可以直接反映裂隙系统随尺寸的变化规律，其中P32单位为m2/m3，P31单位为条/m3，两者均可体现岩体内裂隙的发育程度。

基于构建的不同尺寸裂隙网络模型，编制Fish语言计算得到P32和P31随裂隙网络模型尺寸的变化规律，如图3和图4所示，其中1、2、3、4、5分别代表5个不同的三维裂隙网络模型，不同尺寸均值用实线相连。从P32随模型尺寸的变化规律来看，当模型尺寸较小时，相同尺寸岩体模型所得P32的离散程度很大，同时P32均值在不同尺寸岩体模型之间的波动较大；随着模型尺寸的增大，相同尺寸岩体模型所得P32的离散程度逐渐减小，P32均值在不同尺寸岩体模型之间的波动也逐渐减弱，趋于一个稳定值。P31随模型尺寸的变化规律呈现与P32相似的特征，样本数据的离散程度和样本均值随模型尺寸的增大逐渐减小，最后趋于稳定。究其原因，当模型尺寸较小时，模型内部包含有少量裂隙或没有裂隙，样本差异性大，因此P32和P31的离散程度也很大，随着模型尺寸的增大，模型内部包含的裂隙逐渐呈现相似的统计规律，P32和P31趋于稳定。

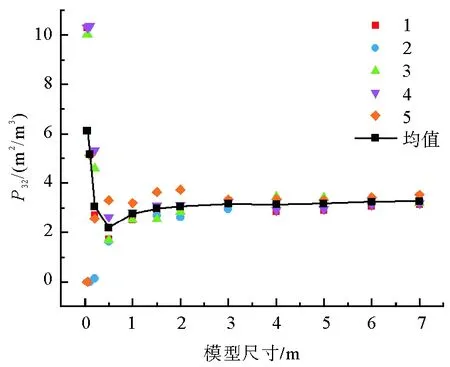
图3 P32与模型尺寸的关系Fig. 3 Relationship between P32 and model size

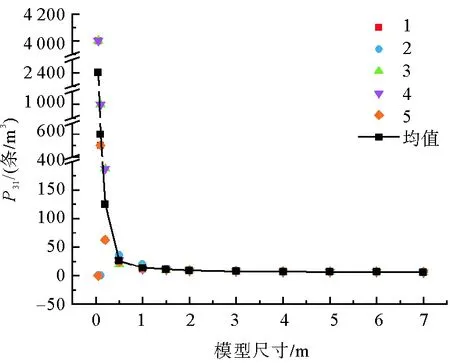
图4 P31与模型尺寸的关系Fig. 4 Relationship between P31 and model size

针对尺寸效应所表现出来的两种特征，采用变化差值率和变异系数两个指标相结合的方法来对岩体REV尺寸进行量化分析。变化差值率用来反映相邻尺寸对应数值的波动大小，其表达式为：

(1)

式中：εi为第i级尺寸的变化差值率；Pi和Pi-1分别为第i和i-1级尺寸对应的数值。变异系数是标准差与平均值的比值，用来反映1组数据的离散程度[18]，其表达式为：

(2)

式中：cv为变异系数；σ为标准差；μ为平均值。表3列出了P32和P31的变化差值率及变异系数，本研究设定变化差值率小于10%和变异系数小于10%作为REV尺寸的量化指标，也就是当计算参数同时满足这两个指标时，即认为达到稳定。从P32的角度来看，模型尺寸从3 m到4 m，P32均值的变化差值率为0.60%，同时模型尺寸为3 m时的变异系数为4.05%，均小于10%；另外当模型尺寸大于3 m时，变化差值率和变异系数也均小于10%，故根据P32确定的REV尺寸为3 m×3 m×6 m。从P31的角度来看，模型尺寸从3 m到4 m，P31均值的变化差值率为9.92%，同时模型尺寸为3 m时的变异系数为2.86%，均小于10%；并且当模型尺寸大于3 m时，变化差值率和变异系数也均小于10%，故根据P31确定的REV尺寸也为3 m×3 m×6 m。综合来看，根据P32和P31得到的REV尺寸均为3 m×3 m×6 m，因此确定裂隙岩体的几何REV尺寸为3 m×3 m×6 m。

2 力学REV尺寸的确定

等效岩体模型以颗粒流软件PFC3D为实现平台，由黏结颗粒模型和裂隙网络模型构成，分别用来表征完整岩块和裂隙[19]。黏结颗粒模型是将刚性球体颗粒在接触点黏接在一起，本研究通过赋予平行黏结模型来描述颗粒接触的力学特征。将裂隙网络模型嵌入黏结颗粒模型当中，裂隙面穿过的颗粒接触由原来的平行黏结模型替换为光滑节理模型，便可构建等效岩体模型。通过对等效岩体模型进行各种加载条件下的力学试验，便可得到裂隙岩体的各种力学特征。

2.1 完整岩块的细观参数标定

颗粒流理论采用细观参数表征颗粒和黏结的力学性质，因此为了使生成的黏结颗粒模型能够真实反映完整岩块的力学性质，需要通过单轴压缩数值试验，不断调整黏结颗粒模型的细观参数来匹配设定的宏观参数。完整岩块的宏观参数采用实验室力学试验得到的花岗岩力学参数，单轴抗压强度为221 MPa，弹性模量为69 GPa，泊松比为0.22[20]。为了消除黏结颗粒模型本身可能存在的尺寸效应，将每个尺寸的黏结颗粒模型的宏观参数都标定到给定的数值[21]。

黏结颗粒模型细观参数的标定过程：首先通过标定法向刚度比kn/ks得到泊松比v，然后对有效模量Ec进行修正，得到目标弹性模量E，最后对法向黏结强度σc和切向黏结强度τc进行修正，以获得目标单轴抗压强度。经过反复的调试，黏结颗粒模型选取的细观参数见表4。黏结颗粒模型经过单轴压缩数值试验计算得到的宏观参数见表5，其与实验室测试结果都比较接近。

2.2 裂隙的细观参数标定

光滑节理模型被用来模拟裂隙面的力学行为，可以消除传统方法采用强度较弱的黏结接触模型时表现出的颠簸效应[19]。裂隙细观参数的标定通过构建包含水平贯穿裂隙面的岩体数值模型，进行不同正应力作用下的直剪试验，通过不断调整光滑节理模型的细观参数，最终获得与实验室结果匹配的数值试验结果。裂隙的宏观力学参数取：黏聚力0.1 MPa，内摩擦角27°。

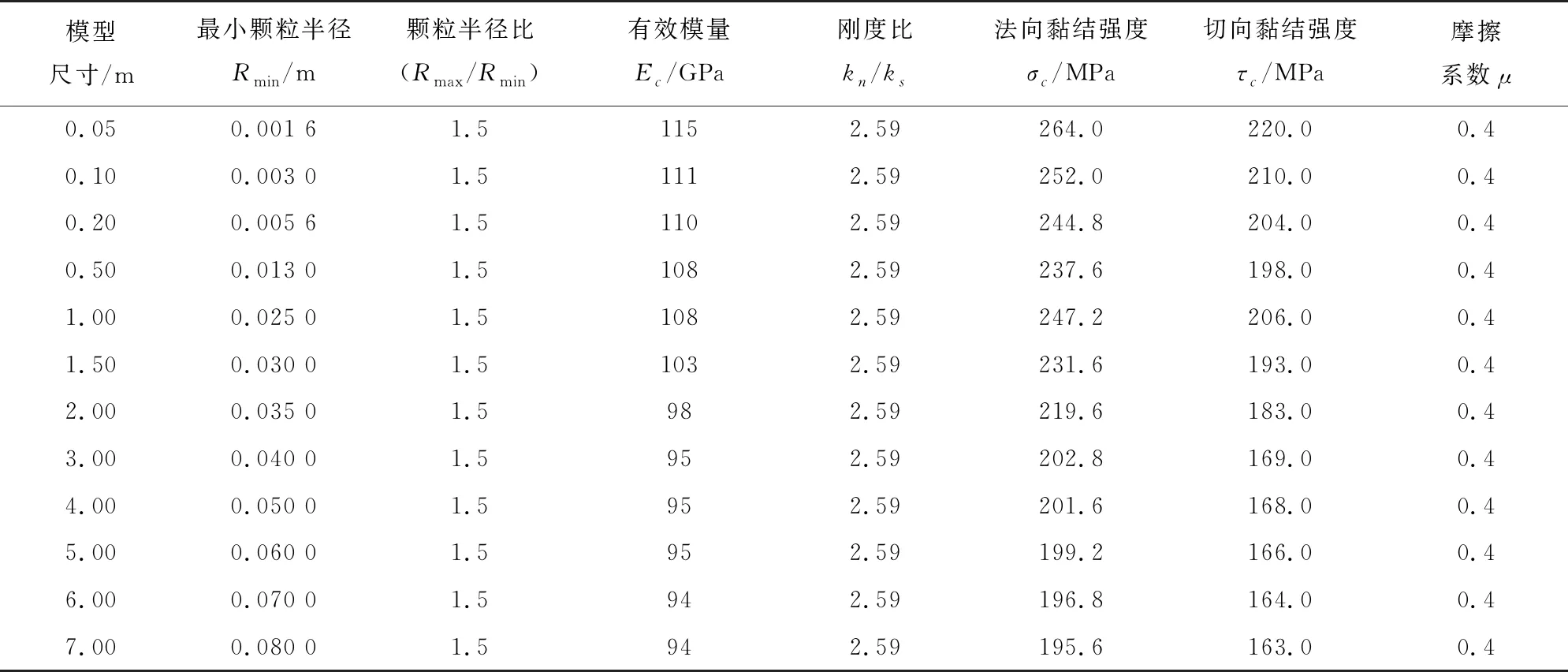
表4 黏结颗粒模型的细观参数Tab. 4 Mesoscopic parameters of bonded particle models

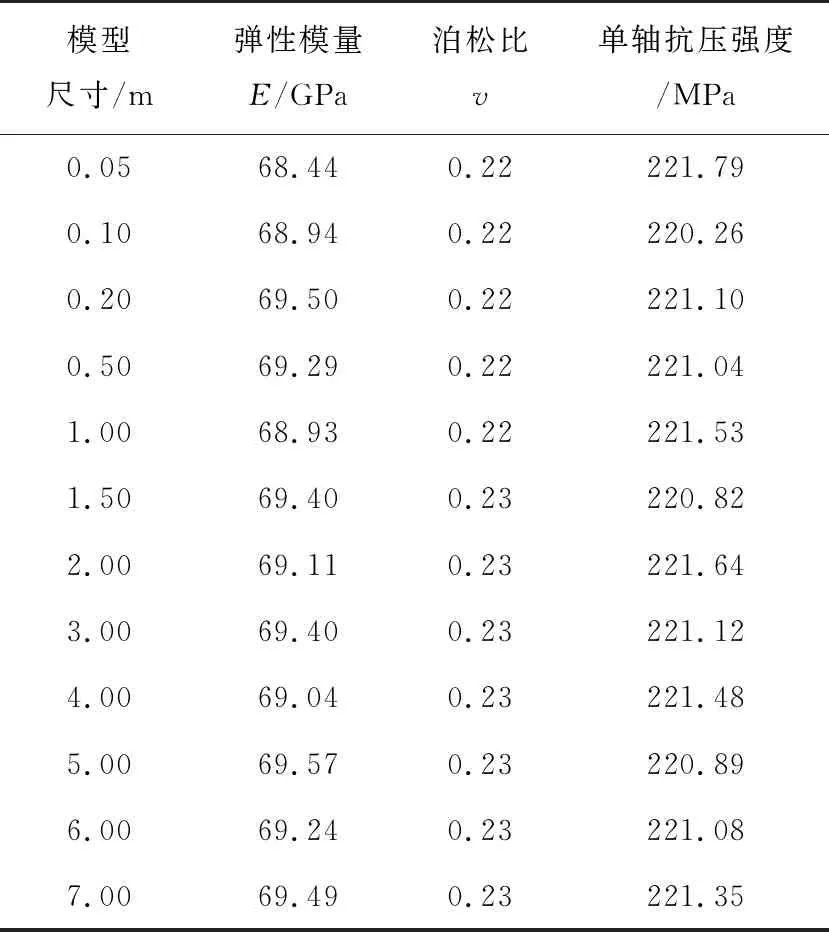
表5 黏结颗粒模型的宏观参数Tab. 5 Macroscopic parameters of bonded particle models

直剪试验采用边长为0.1 m的立方体模型。裂隙面位于模型的中间位置，并被赋予光滑节理模型，分别进行正应力为1.0、2.0、3.0、4.0和5.0 MPa的直剪试验，记录抗剪强度并拟合裂隙强度包络线。经过反复试算，最终获得与实验室结果较为接近的裂隙宏观力学参数，裂隙的强度包络线如图5所示，所选取的裂隙的细观参数见表6，并应用于所有的裂隙。

2.3 不同尺寸的等效岩体模型

根据表4中完整岩块的细观参数建立不同尺寸的黏结颗粒模型，然后将1.2节生成的裂隙网络模型嵌入到对应尺寸的黏结颗粒模型中，交叉位置赋予光滑节理模型，其细观参数取值按表 6所示，由此便可构建不同尺寸的等效岩体模型。共生成60个等效岩体模型，图6为以其中一个三维裂隙网络构建的等效岩体模型。裂隙网络模型本身并不参与计算，仅起到定位与识别光滑节理模型赋予对象的作用。

2.4 力学REV尺寸

基于上述构建的不同尺寸等效岩体模型，分别开展一系列单轴压缩试验，根据单轴抗压强度和弹性模量的尺寸效应来综合确定单轴压缩试验条件下的力学REV尺寸。

通过单轴压缩试验计算得到不同尺寸等效岩体模型的单轴抗压强度和弹性模量，如图7和图8所示，其中1、2、3、4、5分别代表基于5个不同裂隙网络模型构建的等效岩体模型，不同尺寸均值用实线相连。结果表明，单轴抗压强度和弹性模量都表现出明显的尺寸效应，当模型尺寸较小时，同一尺寸岩体模型的单轴抗压强度和弹性模量的离散程度很大，同时两者的均值在不同尺寸岩体模型之间的波动较大，随着模型尺寸的增大，同一尺寸岩体模型的单轴抗压强度和弹性模量的离散程度逐渐减小，两者的均值也逐渐趋于稳定。与单轴抗压强度相比，弹性模量的变化幅度相对较小。

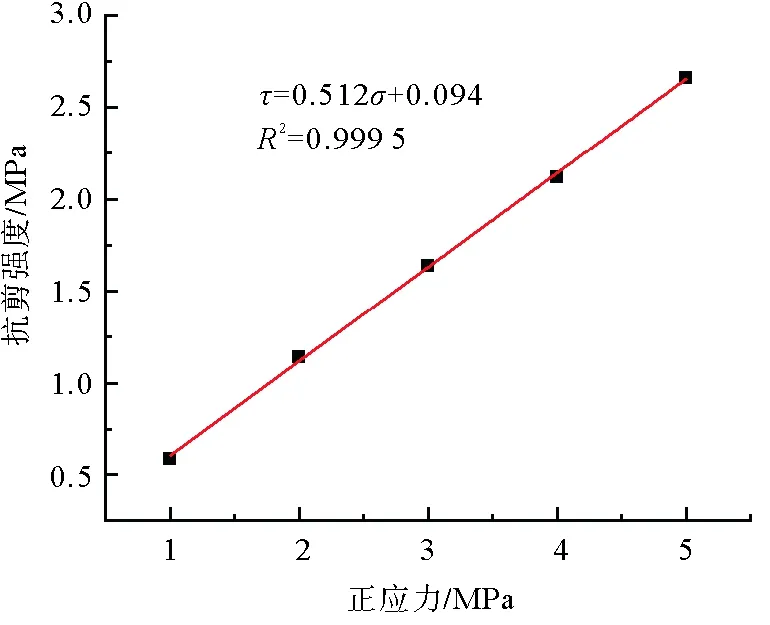
图5 裂隙的强度包络线Fig. 5 Fracture strength envelope

表6 裂隙的细观参数Tab. 6 Microscopic parameters of fractures

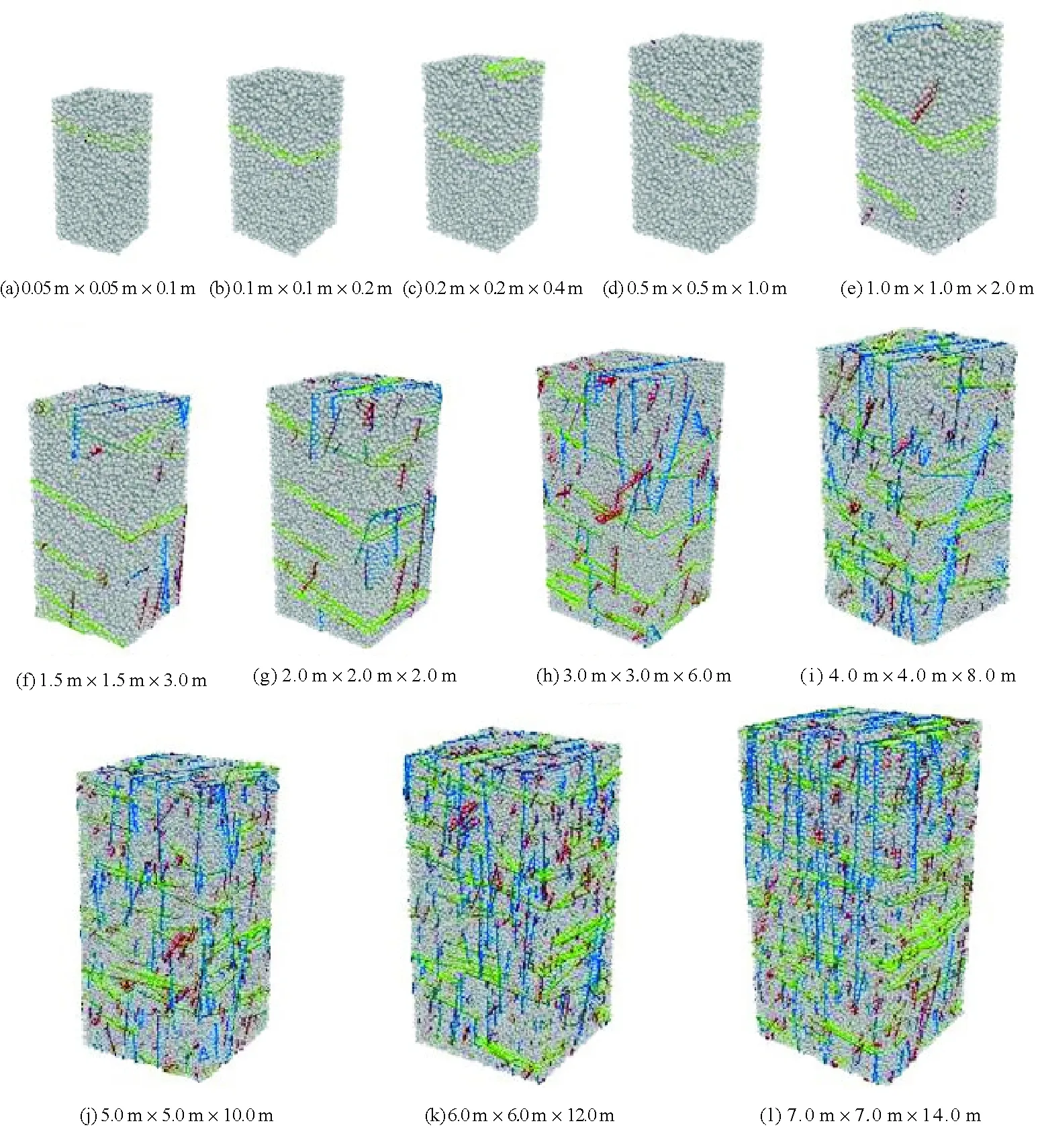
图6 不同尺寸的等效岩体模型Fig. 6 Synthetic rock mass models of different sizes

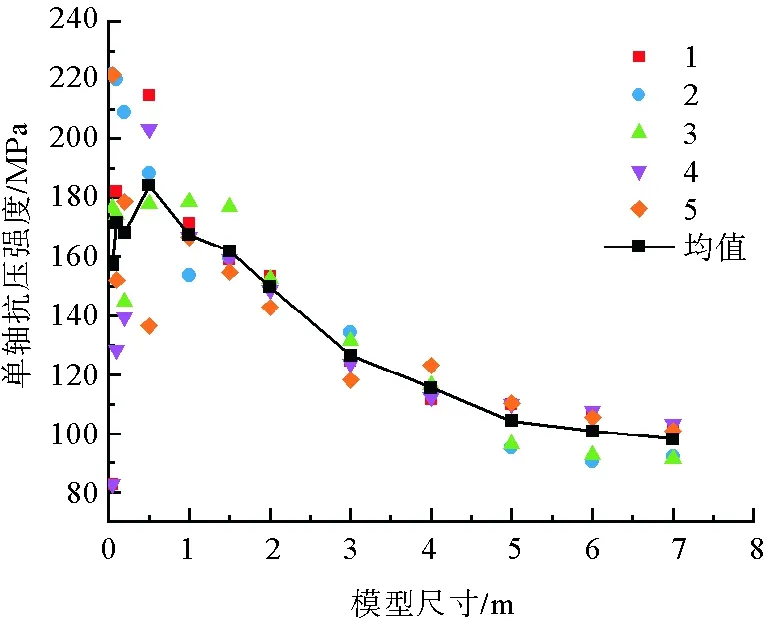
图7 单轴抗压强度与模型尺寸的关系Fig. 7 Relationship between uniaxial compressive strength and model size

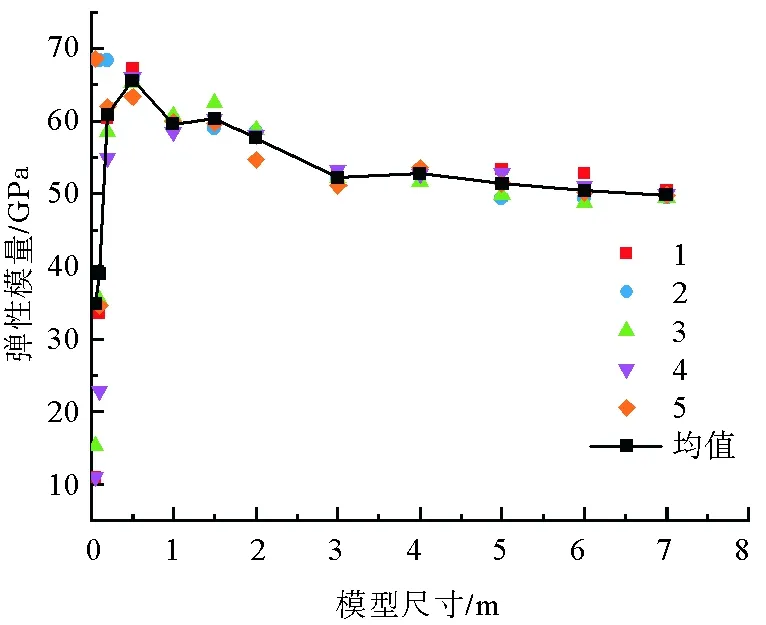
图8 弹性模量与模型尺寸的关系Fig. 8 Relationship between elastic modulus and model size

表7列出了单轴抗压强度和弹性模量的变化差值率和变异系数，同样设定变化差值率小于10%和变异系数小于10%作为REV尺寸的量化指标。从单轴抗压强度来看，模型尺寸从5 m到6 m，单轴抗压强度均值变化差值率为2.62%，同时模型尺寸为5 m时的变异系数为7.65%，均小于10%；并且模型尺寸大于5 m时，变化差值率和变异系数也均小于10%，故根据单轴抗压强度确定的REV尺寸为5 m×5 m×10 m。从弹性模量来看，模型尺寸从3 m到4 m，弹性模量均值的变化差值率为0.97%，同时模型尺寸为3 m时的变异系数为1.49%，均小于10%，并且当模型尺寸大于3 m时，变化差值率和变异系数也均小于10%；故根据弹性模量确定的REV尺寸为3 m×3 m×6 m。

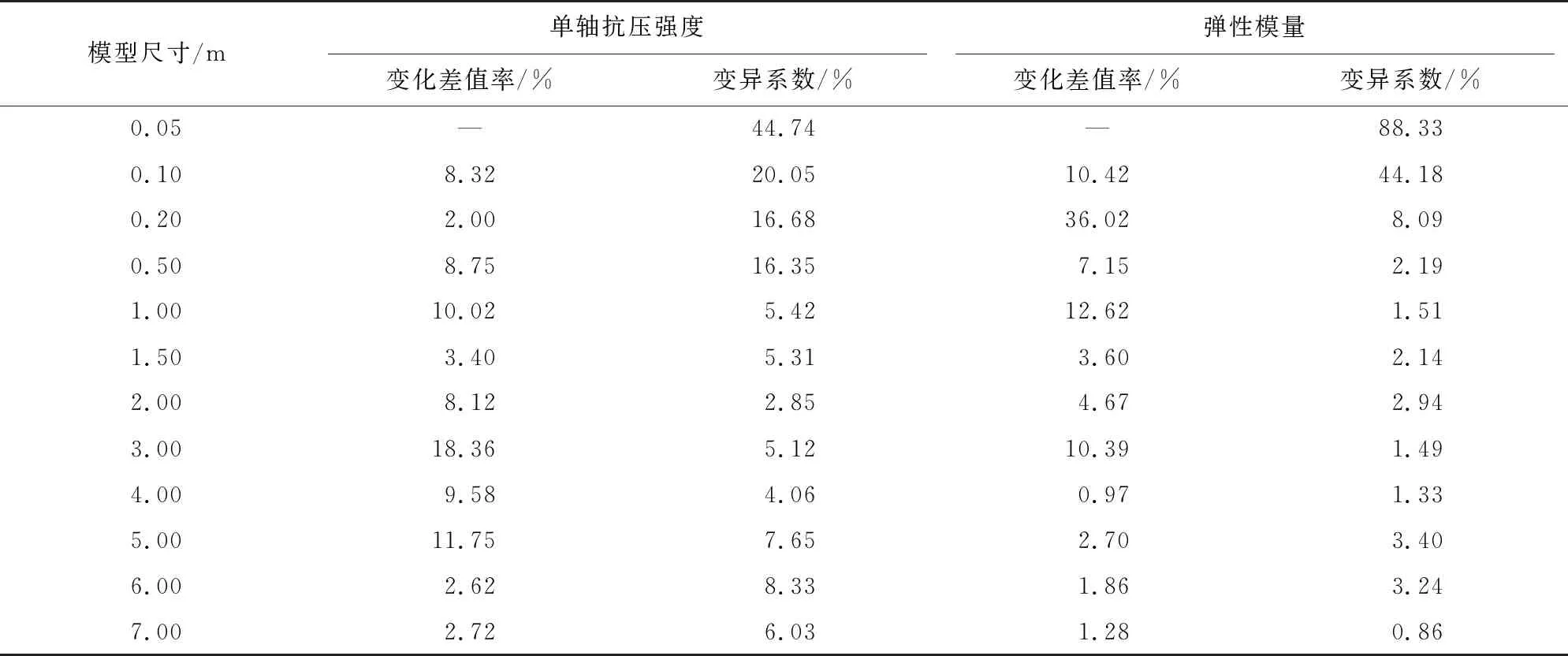
表7 力学参数的变化差值率和变异系数Tab. 7 Change rate and variation coefficient of mechanical parameters

综合来看，单轴压缩条件下，根据单轴抗压强度确定的REV尺寸为5 m×5 m×10 m，而根据弹性模量确定的REV尺寸为3 m×3 m×6 m，因此取其中较大的尺寸5 m×5 m×10 m作为岩体的力学REV尺寸。

3 几何与力学REV对比分析

岩体结构控制论的观点指出，岩体的力学性质是由岩体结构控制的[1]。周创兵等[22]进一步指出岩体力学性质的尺寸效应是由岩体不连续面网络特性所决定的。卢波等[8]提出结构表征单元体(structure REV，SREV)的概念，并指出SREV是岩体REV取值的下限。通常情况下，由岩体的结构特征参数确定的几何REV即为SREV。以上研究表明，不同尺寸裂隙岩体中结构特征的差异性是裂隙岩体力学参数存在尺寸效应的根本原因。几何REV尺寸是代表裂隙岩体结构特征的最小体积，力学REV尺寸是代表裂隙岩体力学特征的最小体积，因此从理论角度可推知，几何REV尺寸小于力学REV尺寸。

对比数值计算得到的几何REV尺寸和力学REV尺寸可知，几何REV尺寸小于力学REV尺寸，该结果验证了上述的理论推断。由此可知，随着岩体尺寸的增加，岩体内部裂隙分布逐渐呈现相似的统计特征，岩体的几何参数先趋于稳定，即先达到岩体的几何REV尺寸；而后结构特征的相似反映到力学特征的相似，岩体的力学参数也趋于稳定，即达到岩体的力学REV尺寸。因此裂隙岩体结构特征的稳定是其力学特征稳定的必要条件，裂隙岩体的几何REV尺寸应该是其力学REV尺寸取值的下限。

几何REV能够反映裂隙岩体的等效结构特性，可以为裂隙岩体结构特性的研究提供依据。力学REV能够反映裂隙岩体的等效力学特性，其对应的力学参数可以作为连续介质方法分析岩体工程问题的输入参数，并且力学REV尺寸可为单元尺寸的选取提供依据。在岩体工程中，当研究裂隙岩体的结构特性时，需选取裂隙岩体的结构特性参数来确定其几何REV；当研究裂隙岩体的力学特性时，则需选取裂隙岩体的力学特性参数来确定其力学REV。

4 结论

利用PFC3D软件，确定了裂隙岩体的几何REV尺寸和力学REV尺寸，并对两者进行对比分析，得到的主要结论如下：

1) 根据裂隙的地质参数，构建了不同尺寸的裂隙网络模型。结果表明，裂隙岩体的几何参数P32和P31表现出明显的尺寸效应，设定变化差值率和变异系数都小于10%作为REV尺寸的量化指标，最终得到裂隙岩体的几何REV尺寸为3 m×3 m×6 m。

2) 结合裂隙网络模型和标定得到的完整岩块和裂隙的细观参数，构建了不同尺寸的等效岩体模型，对其开展了一系列单轴压缩数值试验，计算得到单轴抗压强度和弹性模量随模型尺寸的变化规律。结果表明，单轴抗压强度和弹性模量表现出明显的尺寸效应，同样设定变化差值率和变异系数都小于10%作为REV尺寸的量化指标，最终得到裂隙岩体的力学REV尺寸为5 m×5 m×10 m。

3) 从岩体尺寸效应的本质角度，建立了几何REV尺寸小于力学REV尺寸的理论关系。对比数值计算得到的几何REV尺寸和力学REV尺寸，结果验证了理论推断。几何REV和力学REV分别具有不同的工程特性，应根据不同的工程需求选取相应的表征参数来确定岩体的REV尺寸。