基于弹塑性损伤的软煤水压致裂渗流耦合数值模型

武文宾123

(1. 瓦斯灾害监控与应急技术国家重点实验室，重庆 400037；2.中煤科工集团重庆研究院有限公司，重庆 400037；3.山东科技大学 安全与环境工程学院，山东 青岛 266590)

为解决煤层渗透率低的问题，国内技术人员针对性地研发煤层的各种增渗技术，使煤层中产生人为裂隙或沟通原生裂隙，增加煤层气流动通道，达到提升煤层气抽采效果的目的。目前主要技术有保护层开采的煤层外增渗和包括水力增渗、爆破增渗等的煤层内增渗措施[1]。水力压裂作为水力增渗常用方法，已在能源领域尤其是油气开采中得到广泛应用并取得良好效果。该方法是将流体介质高压注入煤层使其破裂形成贯通裂缝从而形成气体通道，增加煤层渗透率。

在岩石的损伤、渗流等方面已有成熟理论，试验已发现或验证了材料内部的裂隙和应力应变与渗流特性的相关性[2-7]，揭露了不同应力应变条件下的岩石渗透率敏感性及变化规律，发现部分岩石内部损伤应变不可恢复及渗流滞后的现象。由于我国低渗软煤赋存较多，为研究软煤与硬煤的特性差异并指导软煤增渗的实施，诸多学者进行了软煤原始渗流耦合或致裂耦合特性研究，如赵志根等[8-9]研究了软煤非均质性及应力-应变的差异特征。张天军等[10-14]建立了软煤在受载作用时的损伤演化模型、孔隙特征及声发射特征。Fujii等[15-19]通过实验提出了损伤判据、流变模型、孔隙结构及塑性变化等特征模型。

目前针对水力压裂技术的研究主要集中在其增渗工艺和瓦斯抽采作用方面，只是发挥了水力压裂某一方面的有限作用，而井下软煤水力压裂过程中以塑性应变为主要特质的软煤变形、裂纹起裂和增渗规律具有明显的特殊性，尚缺乏理论和实践支撑。利用损伤力学理论对软煤水力压裂裂隙进行定性定量描述，以充分认识软煤塑性变形破坏规律，进而揭示其增渗规律，为井下软煤水力增渗参数优化及技术的应用与推广提供理论依据。

1 数值模型建立

1.1 软煤损伤本构模型

一维应力状态下损伤原理的数学表达式为：

(1)

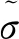
损伤变量的定义依据是Rabotnov假设，以有效应力及名义应力之间的关系进行表征：

(2)

根据式(1)和(2)得到弹性模量法的基本定义形式，并以之作为计算损伤度值的依据，损伤变量D可表示为：

(3)

根据以上定义，单轴压缩条件下的本构关系可表示为：

(4)

剪切状态下的本构关系可表示为：

(5)

推广到三维应力状态，其本构关系可表示为：

σij=2μ(1-D)εij+λ(1-D)εkkδij。

(6)

式中：σij为应力分量；εij为应变分量；λ、μ为拉梅常数。

软煤是一种颗粒+胶结物形式存在的一种岩石介质，在外力作用下往往发生颗粒滑动，表现为剪切破坏。软煤水力压裂是软煤在水力剪切作用下内部颗粒发生剪切滑动，并相互贯穿而产生煤体损伤，继而提高软煤渗透率的增渗技术，其破坏准则通常选用屈服准则。Mohr-Coulomb屈服准则是一种基于Mohr-Coulomb强度准则的常用于岩石类材料的弹性理想塑性屈服准则。不考虑损伤情况下，Mohr-Coulomb强度准则认为当岩体发生剪切破坏时，破坏面上的切应力τn与正应力σn满足[20-22]

τn=C+σntanφ。

(7)

式中：φ为内摩擦角，(°)；C为内聚力，MPa。Mohr-Coulomb屈服准则可以用应力不变量进行表征：

(8)

或

(9)

若Mohr-Coulomb屈服准则考虑损伤的影响，则可用有效应力替换上式中的名义应力，即：

(10)

利用损伤变量，得到考虑损伤影响下由名义应力表示的Mohr-Coulomb屈服准则为：

(11)

以应力不变量形式表达的若Mohr-Coulomb准则为：

(12)

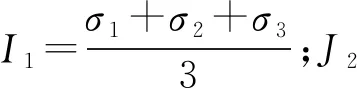
1.2 基于应变等效假说的软煤损伤本构模型

软煤作为一种典型的非均匀多孔介质材料，当外载荷比较小，即软煤整体仍处于弹性阶段的时候，其渗透率的变化可以通过孔隙度或体积应变的改变来描述，按照渗流的立方体规律可表示为：

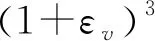
(13)

当所受应力达到一定强度，软煤内部的微孔洞、裂隙等将发生扩展汇聚，损伤开始产生。随着加载的进一步进行，损伤不断增加，导致渗透率发生较大改变。在流固耦合作用下，考虑损伤影响时，只计算体积应变的影响研究渗流规律，将会产生比较大的误差。

随着载荷的增加，软煤内部开始出现损伤，由于损伤区域渗透性能强，导致表征体元的渗透率增大；随着损伤的发展，表征体元的渗透率加速增加；当损伤发展到一定程度，损伤区域增加变小，甚至损伤区域可能发生错动等变化，导致加载后期渗透率增加变缓，甚至减小。

基于以上分析，令表征体元中未损伤部分渗流流量为qM，损伤部分的渗流流量为qD，则渗透率计算公式为：

(14)

式中，ΔP为表征体元上下端注水压差，μ为注水黏度。考虑表征体元未损伤和损伤部分的截面积，式(14)可进一步表示为：

k=(1-D)kM+DkD，

(15)

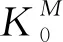
(16)

将式(16)变为量纲的形式，有：

(17)

2 基于FLAC3D模型数值求解

2.1 求解模型及边界条件

利用FLAC3D中的编程功能引入上述关系方程进行数值求解，具体步骤如图1。

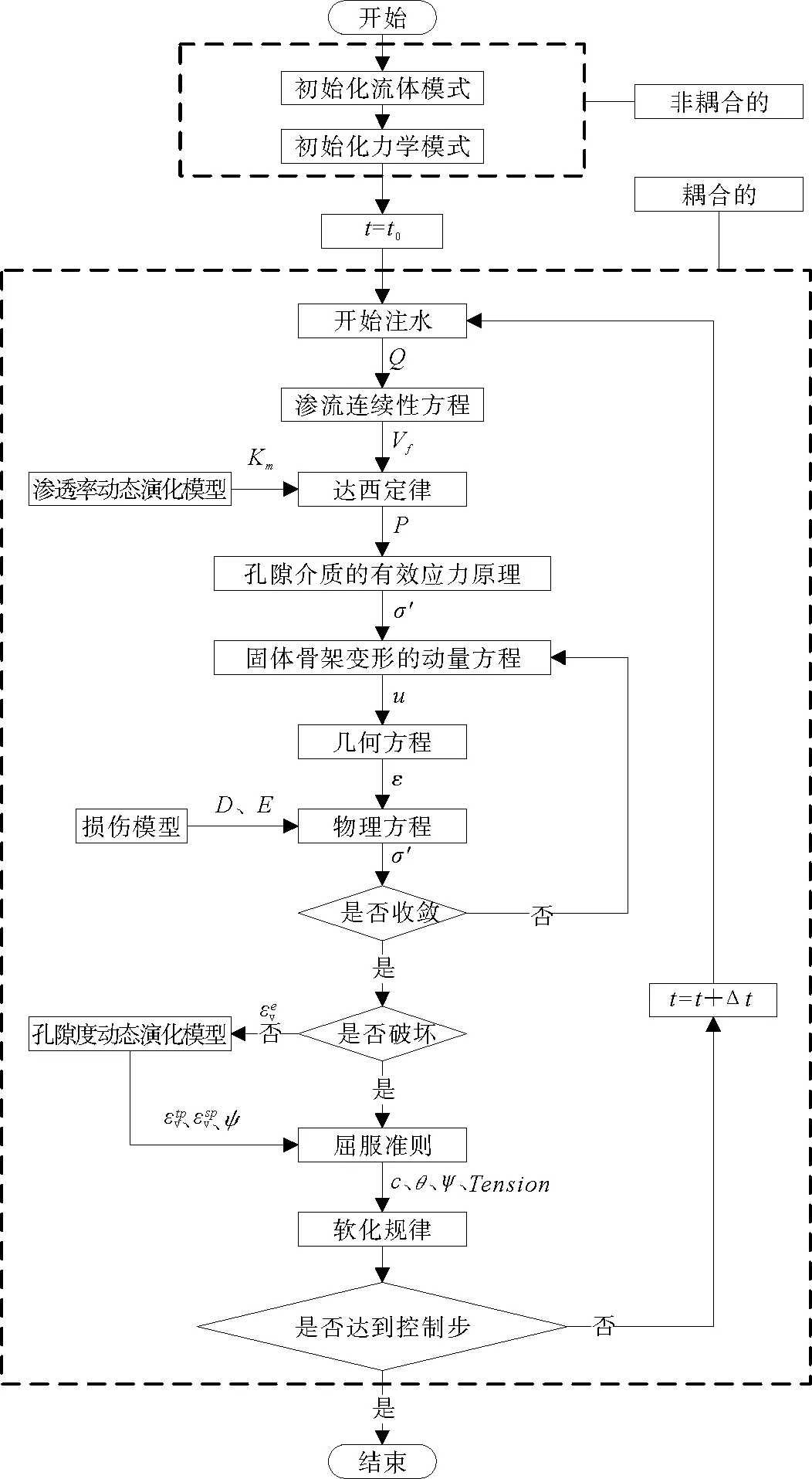
图1 求解流程

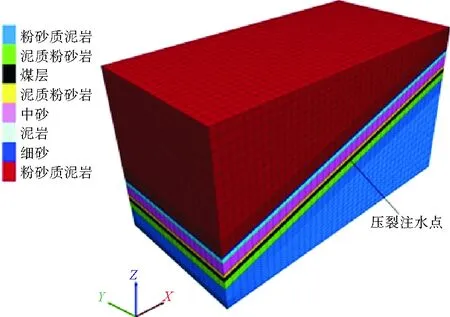
图2 几何模型

设置200 m(x)×200 m(y)×112 m(z)的对称三维模型，对模型划分网格共生成60 270个节点，55 200个单元，如图2所示。

将模型顶部和底部设定为约束面，设定煤层受多层上覆岩体的垂直应力为12 MPa，x方向和y方向的侧向应力系数分别为1.8和1.3，设定1 MPa的煤层内初始孔隙压力，设定煤岩体的抗拉强度为0时塑性拉伸临界值为1×10-4。

2.2 水压致裂变参数规律

如图3所示，压裂半径随压入流量的增加先增大而后下降，由于小流量压入时的总时长较长，导致滤失较大，故压裂半径小；在大流量情况下，压裂半径呈下降趋势。

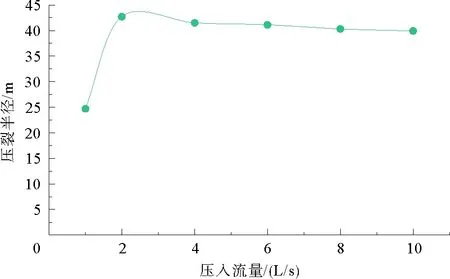
图3 压裂半径受压入流量的影响Fig. 3 Influence of water injection rate on fracture radius

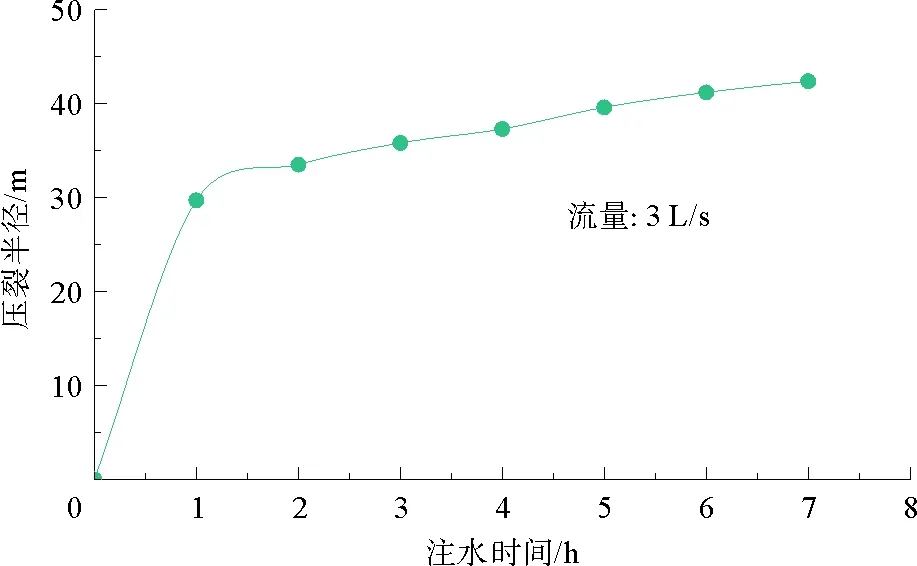
图4 压裂半径受压入总时间的影响

如图4所示，当流量3 L/s时，压裂半径受压入总时间的变化而影响。初始情况下至1 h间压入水量初始填充钻孔附近裂隙煤体，压裂半径变化快，之后由于内部水压及阻力存在，压裂半径增长较慢且趋于线性稳定。

2.3 模拟结果分析

图5和图6分别为3 L/s流量，总压入水量150 m3结束后的孔隙度正视和切面云图。孔隙度在压裂半径内并非均匀分布，而是形成从中间到边缘的高到低分布，还可以体现渗透率在煤体中的空间特征。

图5 X-Z平面孔隙度云图Fig. 5 Porosity contour of X-Z plane

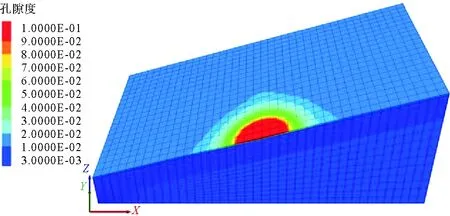
图6 沿煤层切面孔隙度云图

图7和图8分别为体塑性拉伸和剪切应变云图，煤体在压裂过程中同时发生剪切和拉伸破坏，剪切破坏在顶底板中表现出了顶高底低的分布规律，受重力影响较小，且与主应力无明显的夹角关系，符合软煤压裂中的应力应变关系。

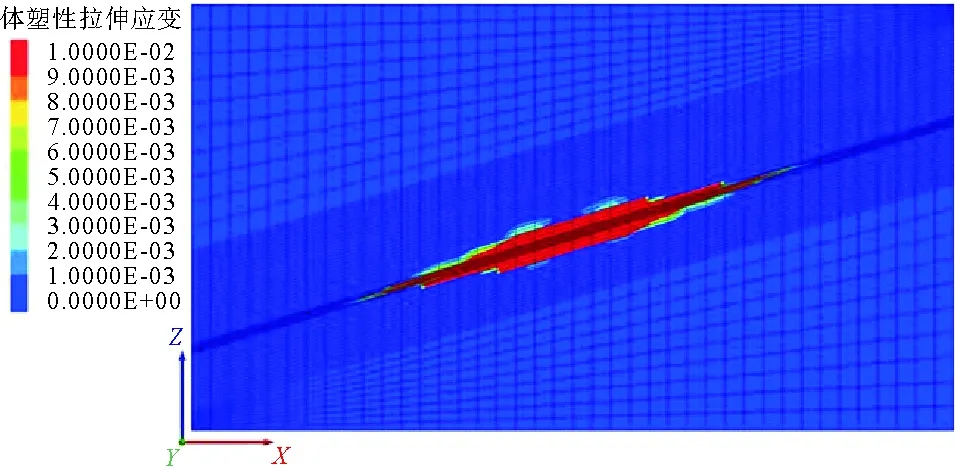
图7 X-Z平面体塑性拉伸应变云图Fig. 7 Plastic tensile strain contour of X-Z plane

图8 X-Z平面体塑性剪切应变云图

2.4 硬煤与软煤数值计算差异化分析

软煤相对硬煤差异性规律仍然采用图2模型，煤层采用传统弹性变形理论及裂缝流动与扩展理论，利用相同的边界条件进行模拟计算，分析不同流量与相同流量不同注水时间的差异性。硬煤的耦合控制模型为：分别采用线弹性理论控制煤岩变形、N-S方程和质量守恒方程控制裂缝面内流体流动、线性黏结单元模型来模拟裂缝的扩展。

如图9，压入流量由1 L/s增大到2 L/s时，硬煤和软煤压裂半径均增长较快，但再在一定程度继续增大流量时，软煤的压裂半径变化不大，而硬煤的压裂半径仍有上升趋势。这是由于硬煤相对于软煤存在裂缝扩展，裂缝的导流使得裂缝长度与范围持续扩大。同理如图10，固定3 L/s流量，总压入水量为150 m3时，硬煤在1 h之后的压裂半径近似线性增长且斜率较大，而软煤斜率较小。

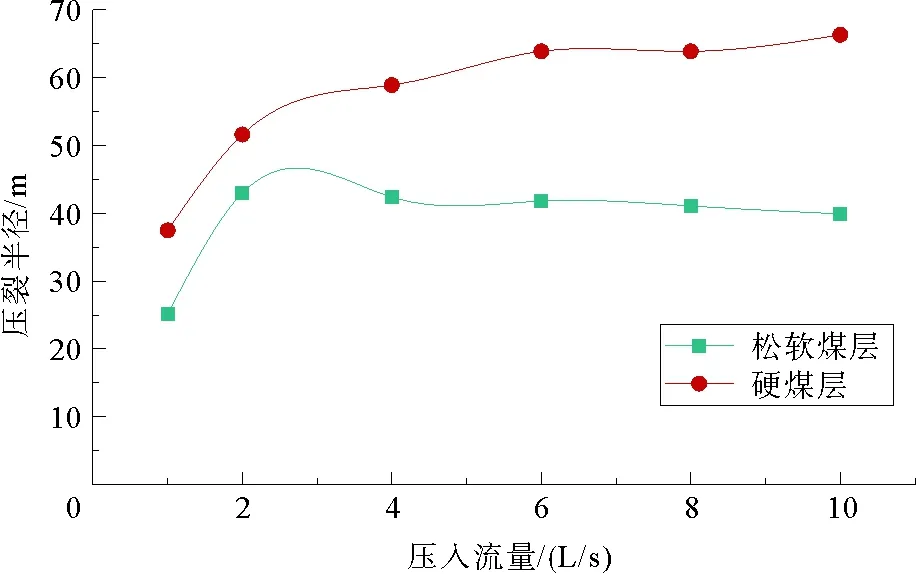
图9 压入流量对硬煤软煤压裂半径的差异规律Fig. 9 Difference rule of water injection rate to fracture radius of hard coal and soft coal

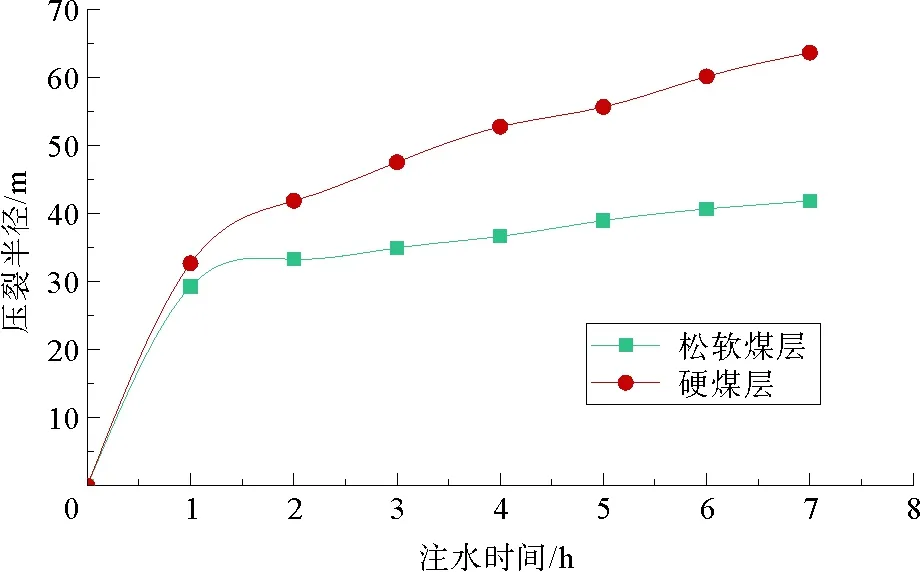
图10 注水时间对硬煤软煤压裂半径的差异规律

3 现场验证

为验证数值计算模型的准确性，在某矿井下15#煤层15403工作面设计水压致裂钻孔进行现场试验，平均流量6.4 L/s，总历时7.5 h，总压入水量167 m3，现场水压致裂施工的压力曲线如图11。为验证压裂半径，在施工抽采钻孔时，按10 m间距分别在走向和倾向上风排煤粉考察煤粉湿润情况或渗水情况，水压致裂范围考察方法及结果示意如图12，压裂后出现了倾向方向压裂范围大于走向方向的现象，这是由于受地应力影响所致，在倾向上的压裂范围为60 m，在走向方向上的压裂范围为40 m。

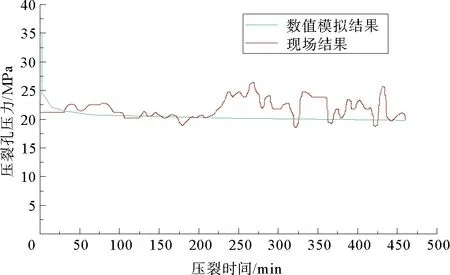
图11 现场压力控制情况Fig. 11 Field pressure control

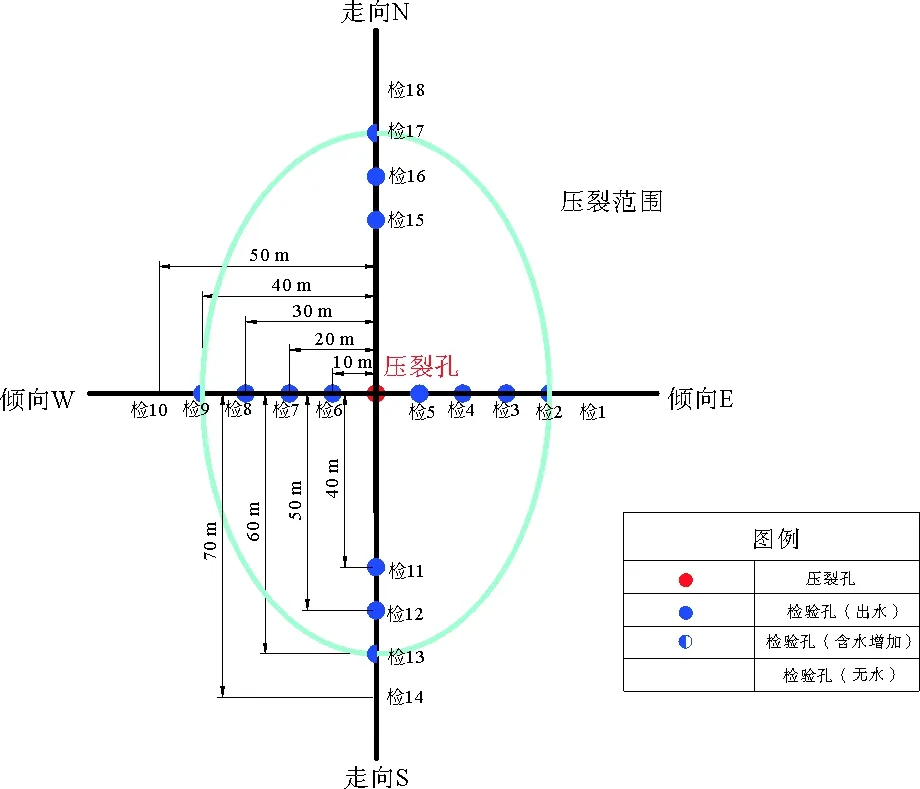
图12 水压致裂考察范围

4 结论

1) 推导出基于应变等效假说的塑性损伤模型和渗透率变化关系，形成水压致裂的应力-渗流耦合模型和水压致裂煤体失效判据。

2) 软煤在压裂过程中同时发生剪切和拉伸破坏，小流量压裂时压裂半径小，大流量压裂时压裂半径大，同时出现压裂范围在倾向方向大于走向方向的特征。

3) 数值模拟表明，软煤压裂数值计算模型符合实际规律，现场实验对压裂半径的考察与数值模拟相符。