重大事件下的路网交通疏散双层优化模型

徐泽洲1,2，刘祥泽2，贾彦峰，赵梓旭

(1.青岛市城市规划设计研究院，青岛 266071；2.日照职业技术学院，日照 276800；3.青岛理工大学，青岛 266520)

重大事件按照是否具有可预见性通常分为重大突发事件和重大活动事件，不论何种事件发生都会对周边交通造成拥堵，甚至导致区域交通运行瘫痪。因此，快速疏散事件造成的交通拥堵，一方面反映城市交通治理的水平，另一方面能够提升市民对出行服务的满意度。早在20世纪70年代，Hans等[1]提出了用于估算拥堵疏散时间的简单统计公式，又称为疏散率模型，这是最早用于疏散分析的模型。之后不断有学者对交通疏散过程中的控制策略进行研究，主要包括：逆行车道设计、交通信号控制、疏散路径选择等。逆行车道设计即将车道的行驶方向改为相反方向，能够在短时间内增加特定方向上的通行能力,具有其他组织方式无法比拟的优点,因此采用设置逆向车道能够极大地提高疏散效率,减少重大事件给交通系统带来的危害。Kim等[2]、Zou等[3]的研究说明了逆向车流设计在交通疏散中的有效性，并使用启发式算法求解了疏散时间；Wang等[4]通过仿真软件研究大规模路网的路径优化问题，利用智能算法求出给定时间内的逆向车道的动态设置方案；Mitchell等[5]在研究逆向车道设置问题时，考虑影响路网通行能力的因素，并将其换算成可计算的数学参数，认为逆向车道设置方案还受疏散范围内网络的人口密度、安全出口的距离等因素影响。在交通信号控制方面，Chen等[6]利用动态交通分配模型对应急交通疏散进行了研究，通过实时交通管理控制使整个疏散时间最少；Sisiopiku等[7]用Synchro软件获得了一个小区域的最优配时方案，并利用Corsim软件对疏散方案和信号配时方案进行了评估；Ming等[8]利用Corsim软件评估了美国华盛顿特区两条主要疏散通道上的4种配时方案：红闪方案、黄闪方案、最小绿灯时间方案和高峰小时方案。在疏散路径选择方面，高明霞等[9]将疏散问题视为最大网络流问题，给出了两种寻找最优疏散路径的方法；Dunn等[10]研究核电站发生重大事件情况下的疏散优化问题，考虑在特定时间内建立疏散人群最多为目标的最大流模型;高明霞等[11]对城市路网发生突发事件时，如何对疏散路径进行优化的问题进行了研究，其将城市道路网抽象为便于计算的点权网络，然后将交叉口通行能力以及延误时间定义为网络中的节点权重，建立最小费用流模型并求解最佳线路。孔祥春等[12]所建立的模型考虑了文献[11]中忽略路段通行能力的上限问题，通过减少车辆在交叉口冲突点的延误，达到缩短疏散时间的目的;杨帆等[13]对路网中存在大型活动时的紧急疏散优化进行研究，并考虑交通流特性等参数，建立了动态交通流模型求解疏散路径，并通过单行设置算法得到路网中的疏散状态和疏散需要的时间，求解过程在动态分配算法的基础上完成，最后生成的紧急疏散方案更具有可行性；王健等[14]建立了考虑车道的交通疏散模型，为紧急疏散方案提出一些建议；陈岳明等[15]建立以到达疏散终点的总时间为目标函数的模型，提出动态分配模型用来解决疏散路线选择问题；吴薇薇等[16]探讨了疏散路网的改造方案，并建立了最小饱和流模型，对改造后的方案性能进行分析。

综上，当前我国针对重大事件的交通组织和信号控制相结合的疏散策略研究较少。具体表现在：在现有的基础设施条件下，对事件期间的交通态势的规律和特点把握不充分，在时空(交通信号控制与车道功能设置)角度对交通疏散的优化效果不够理想。对此，本研究构造了一种基于双层结构的交通疏散优化模型。该模型的上层为交通组织优化模型，下层为交通信号控制优化模型，在上层交通组织优化的基础上，再以整体交通系统的总延误时间最小为目标进行再次优化，通过多次迭代后达到模型的平衡状态时输出问题最优解，进而达到快速疏散交通拥堵的目的。

1 双层优化理论与模型

重大活动事件在不同发展阶段表现出不同的特点。城市交通系统以已有的控制策略运行直至活动事件发生，活动事件发生导致城市局部区域的交通出行量急剧变化，在节假日尤其明显且该状态会持续到事件完全解除。本研究提出的双层优化模型是在重大活动事件发生的背景下建立的，主要思路是首先对交通进行上层的组织优化，包括对所在层的目标函数进行相关优化；下层是以上层优化结构作为参数进行交通信号控制优化。其数学表达形式为：

minF(x,y(x))，

(1)

s.t.G(x,y(x))≤0。

(2)

其中，y=y(x)，由下层数学规划问题决定：

minf(x,y(x))，

(3)

s.t.g(x,y(x))≤0。

(4)

式中：F、f分别为上层、下层优化问题的目标函数；G、g分别为上层、下层的限制条件；x、y分别为上层、下层在针对相关问题时的对策变量。

由上述定义可知，上层依据x的数值进行对应规则的设定，该操作将影响下层交通控制的可行集；下层执行上层的规则，同时将执行结果信息反馈回上层，实现了上下层相互影响制约的效果，y=y(x)表示下层的对策变量y与上层对策变量x呈函数关系。

2 交通疏散双层优化模型建立

重大活动事件下，针对交通状况在不同发展阶段表现出的不同特点，结合双层优化思想构建面向交通组织和交通信号控制的双层优化模型。模型上层为交通组织优化，其措施主要为采用单向交通，利用出行者的路径选择进行构造。模型下层以首次单行优化的基础为前提，对道路交叉口交通信号控制策略进行优化，与上层共同构成双层优化模型，将整体延误最小化、交通流量最大化作为优化目标。

2.1 交通组织上层优化算法

当城市某区域内的某位置有重大活动事件发生时，首先假设该区域的交通为G(N，A)，其是由该区域内所有道路交叉口构成的集合N(n∈N)与所有道路构成的集合A(a∈A)共同组成的，a(i，j)表示首端为i、末端为j的路段。该路段内共包括有r个出行起点和s个出行讫点(1≤r≤R,R为起点个数最大值；1≤s≤S，S为讫点个数最大值)，则此时所需的交通疏散路径集合为qrs。道路网的单行优化的决策变量为路段的单行参数C′a，目标为车辆疏散时间F(C′a)最小[3]。

模型的数学表达式为：

minF(C′a)=∑a∈Axa(t)·τa(xa(t))，

(5)

(6)

xa(t)≥0,τa(T)≥0,frs(t)≥0,qr(t)≥0,

(7)

(8)

式中：xa(t)为单位时间路段a的交通量；τa(xa(t))为车辆通过路段a的用时；frs(t)为r个起点至s个讫点的疏散路径交通流量；qr(t)为r个起点的交通量疏散需求。C′a为本轮单行优化的决策变量，假设路段a(i，j)中有双向车道2N个，则单行车道数目与车道单行变量的关系如图1所示。

图1 车道数和单行变量所存在的关系

上层算法中需要设计最优的单行交通组织方案，将总体疏散时间最小化。式(5)为目标函数；式(6)为交通路网疏散的客观约束条件；式(7)为0或正变量约束条件；式(8)为模型决策信息的位置约束条件，路段单向行驶信息在{-1,0,1}内选择。

考虑到城区的主要干线道路或快速路通常遵循双向通行方式，故该模型在实际使用中不应将所有路段皆设定为单向道路，需要结合实际情况将整体路段集合A中部分非干线设定为单行道路。由活动事件的基本特点可知，活动开始的前期和结束会导致交通量出现大幅波动，静态的交通组织优化方案不能及时响应动态疏散需求，故还需要对静态模型的时间维度离散化，即将本时段的交通组织优化效果作为下一时段的优化依据。经分析可知，时间维度的离散化越具体，对模型的修正效果越好，该过程的数学表达为：

(9)

(10)

(11)

(12)

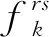
修正的优化模型可将整体时段T分解为n个时长为T/n的时段t1,t2,…,tn，若第ti-1时段中有剩余交通流量，则其会添加到后一个时段ti内，并可经过变换得到：

(13)

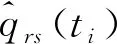
则ti时段的交通通行需求可表示为：

(14)

通过对时段ti的交通通行需求的计算，随后使用Frank-Wolfe算法[17]得到各时间段的交通量及其通行时长。可得修正的总行程时长表达式：

(15)

式中：va0为无约束条件下的车流速度；ea为路段车流密度；la为路段长度。

2.2 交通时序下层优化算法

2.2.1 整体配时策略

单行交通的交通组织方式会将道路交叉口的车辆冲突显著减少，整体延误时间也会随之减少，但该方式会迫使车辆绕行，影响交通的直达性。过量的绕行会一定程度上影响交通参与者的出行体验。因此，还需在单行交通组织方法的基础上对各时间段上的交通信号控制进行优化，以协调相应的交通流量。针对单行交通组织使道路交叉口的冲突点减少的特点，可更大程度发挥“绿波”和“红波”的协调控制优势。

2.2.2 绿波控制

干线绿波控制可有效提高拥堵区域内主干路车辆的通行效率，加快拥堵的疏散。交通信号周期长度可由道路交叉口各进口道的每小时车流量与交通饱和度制定；在交通疏散过程中，信号周期长度的制定还需重点考虑不同路段的车辆蓄存能力以及车辆在不同信号下的到达率等。在上述原则的基础上，若道路交叉口的时空距离过短，则要尽可能使用长周期，在交通流量过大时需对周期长度做必要的限制。综上分析，周期长度计算方法为：

1) 路口的最小通行能力限制：

(16)

2) 交叉口的最大通行能力限制：

(17)

3) 交叉口的最大饱和度限制：

(18)

(19)

式(19)中：ym、y′m分别为相位m的交叉口的流量比与设计流量比；qd为道路交叉口设计交通量；Sd为道路交叉口设计饱和交通量。

绿波控制的周期长度参考符合上述条件的周期的最大值，即

Cref=max(C1,C2,C3)。

(20)

在选用较大周期的前提下，通过调整周期中相位差减少红灯信号时长，在车辆的到达率相同时提高通行效率。基于已有优化策略，引入两个限制条件，即设计相位差避免道路交叉口出现溢流和绿灯损失。

1) 避免溢流的相位差设计

设计过饱和状态的相位差时，将原相位差减少Δr，使停车冲击波的发生时间降低Δr，确保消散点位于道路的上游即交叉口前，如图2所示。假设消散点恰好位于道路上游交叉口处，应用公式(21)计算出相位差的限制：

(21)

式中：ρ为排队长度与路段长度之比；us为离驶冲击波的速度。

2) 避免绿灯损失的相位差设计

在检测到出现绿灯损失时，调整交通信号控制的相位差，使上游交通流在到达道路交叉口时恰好加入下游的道路交叉口放行车队，由此减少绿灯损失时间，如图3。防止绿灯损失的最大相位差由式(22)计算可得：

(22)

图2 防止溢流现象的相位差设计

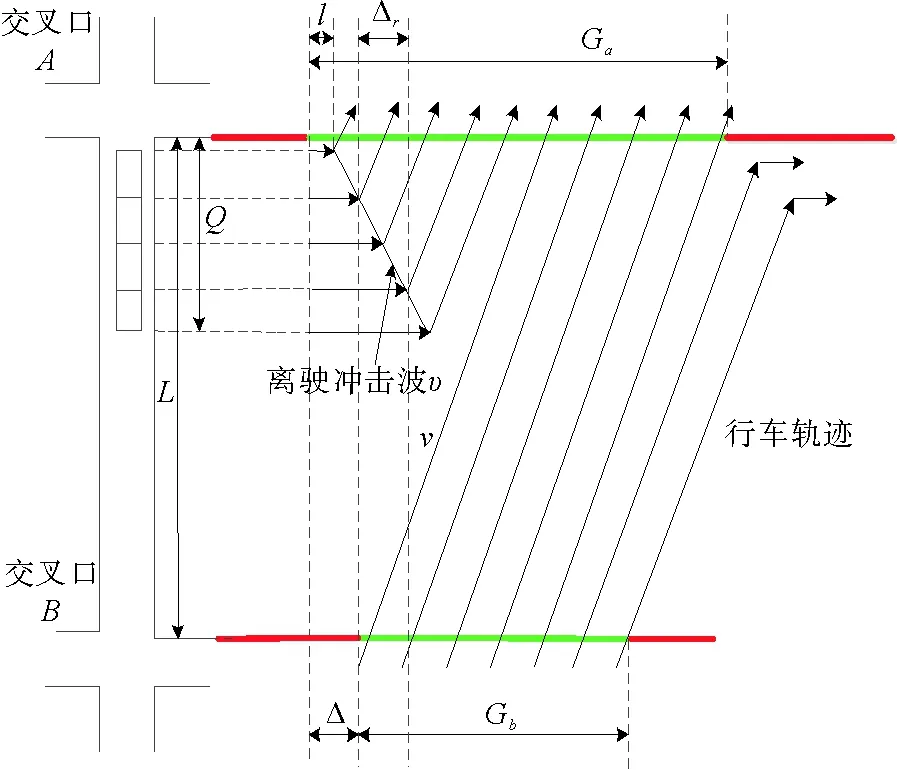
图3 防止绿灯空放的相位差设计

2.2.3 红波控制

重大活动事件结束时会造成局部范围内交通量陡增，此时要优先疏导驶出方向的车辆、减少驶入本区域的外围车辆以缓解活动中心的交通压力。因此，除了要对驶出方向进行绿波协调，还需对驶入方向设定红波。红波控制的起点设置在城区与郊区的交界附近且上游有一定蓄车能力的道路交叉口，下游的交叉口则可按照文献[18]的方法，依据两两相连的交叉口的关联程度来计算和设置信号相位差：

假设Dij为交叉口i与交叉口j的间距，两交叉口所属的路段平均车速为uij，上游车辆经过交叉口时，下游车队在交叉口j的排队长度为Lqj，则上下游车队在下游交叉口相遇时，上游车队行驶的位移长度为：

(23)

式中：nj为单周期内协调方向驶出交叉口j的车辆数目；l为平均车辆纵长；C为信号周期长度。

因此，红波控制的信号相位差设置分为以下2种情况：

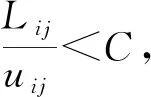
(24)

(25)

(26)

表1 单行通行计算结果

3 数值仿真与验证分析

以青岛某体育场(以红色圆表示)附近区域为例，简化交通路网示意如图4所示。体育场内的重大活动发生后将导致一定时间内该区域的道路对车流量的承载负荷上升，对交通路网运转产生压力，同时由于多数车辆对非主干路的利用不充分，加剧了路网中不同等级道路的使用不均匀不协调。由此，为了加快车辆疏散，需要先以总体疏散延误最小化为目标，依据上层优化模型制定理想状态下的单行交通组织策略，得到表1。

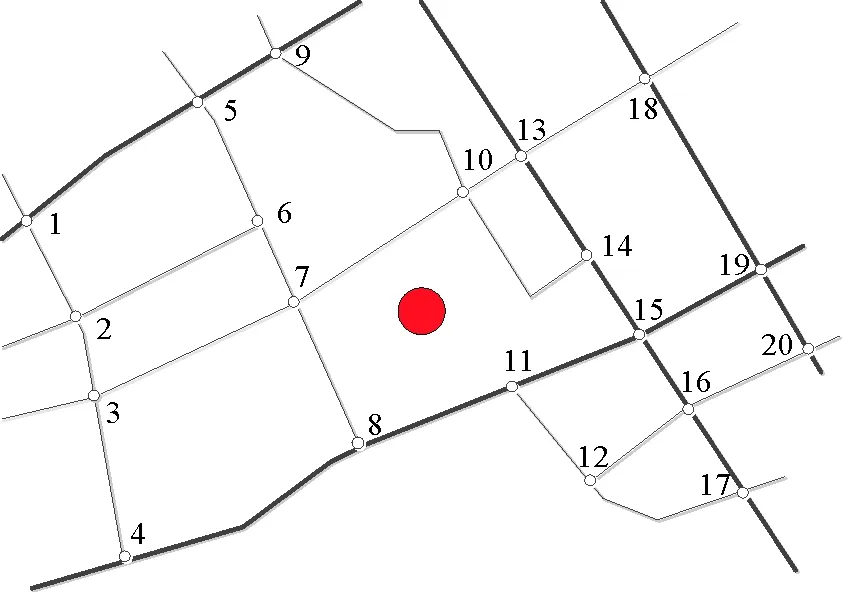
图4 研究区域路网示意图Fig. 4 Schematic diagram of the road network in the study area

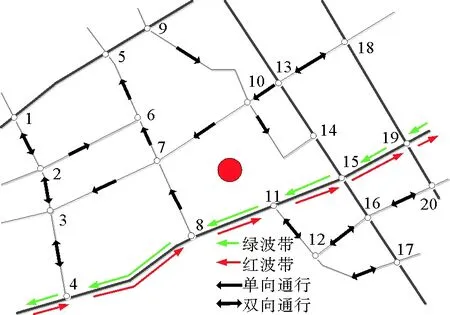
图5 整体控制策略

将表1中的结果进行可视化并以上层模型输出单行优化方案为基础，构建下层的信号协调控制方案，得到的该区域道路网的最终优化策略如图5所示。以活动事件结束期间为例，主干路主要包括编号为4、8、11、15、19共计5个道路交叉口，其他道路交叉口的信号灯配时方案针对上层优化结果进行相应地改动。5个道路交叉口在使用模型优化前的参数如表2所示。根据下层优化模型求得5个路口的参考周期Cref(表3)以及信号相位差限制范围(表4)。

表2 优化前主要交叉口信号配时方案

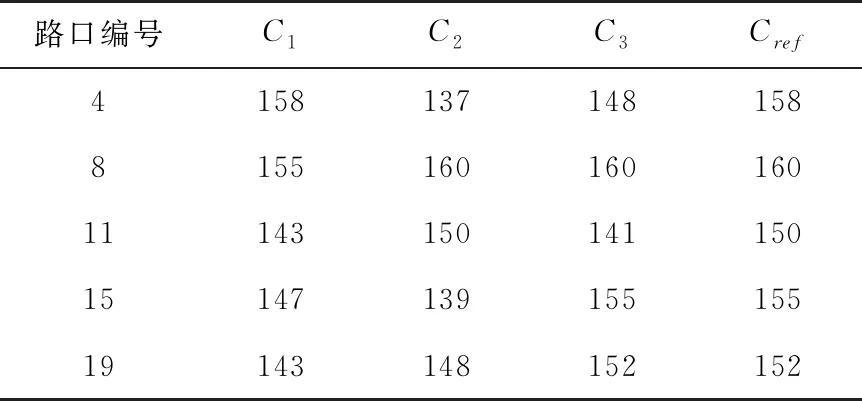
表3 主要交叉口参考周期计算结果

表4 主要交叉口相位差约束区间

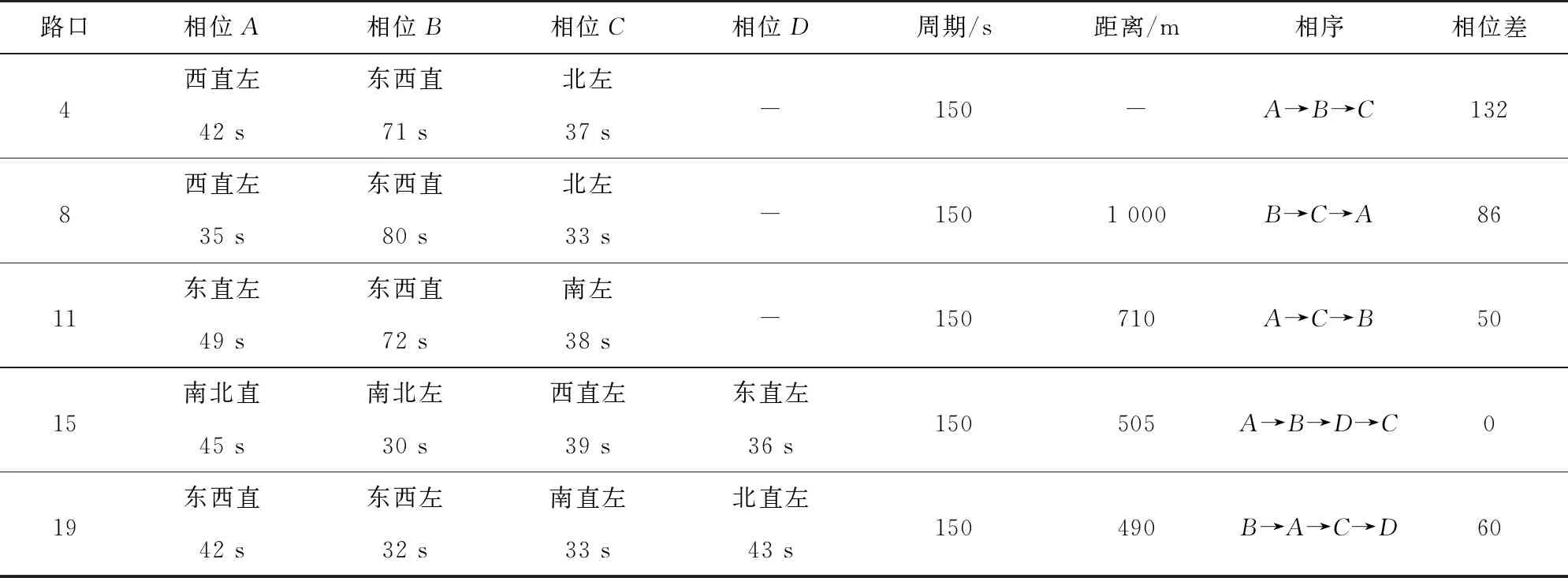
表5 优化后主要交叉口信号配时方案

使用VISSIM软件对主要道路交叉口优化前后的方案进行仿真，仿真步长设置为5，采用连续仿真模式。使用车辆在道路交叉口通过的数目与整体总延误为指标对比优化前后的结果，如图6(a)和图6(b)所示。由图6可见：主要道路交叉口的通行车辆数均得到一定程度提高，平均提高了7.1%，同时5个道路交叉口的车辆总延误平均减少了5.8%。

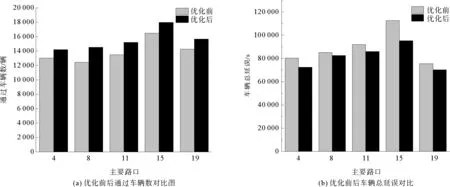
图6 优化前后车辆通过数和总延误对比

4 结论

为缓解重大事件对区域交通产生的影响，将单行交通组织优化结合区域交通信号控制策略两个层面建立交通疏散双层优化模型，该模型可充分考虑到交通组织与交通信号优化的交互影响，通过寻求交通组织与面向交通信号控制的最佳平衡点实现动态最优，同时能保证通行可达性和快捷性，以满足重大活动事件背景下的交通管理要求。仿真结果表明：该模型可有效缓解车流量增加导致的交通压力，使主要道路交叉口的通行车辆数平均提高了7.1%，同时使车辆总延误平均减少了5.8%，证明模型在应对重大活动事件造成的道路交通拥堵有较好的适用性。