基于队列模型生存率数据的跨年度生存患者干预方案医保基金支出的计算方法

黄元楷 陈磊 李莹 席晓宇

中圖分类号 R956 文献标志码 A 文章编号 1001-0408（2021）17-2097-06

DOI 10.6039/j.issn.1001-0408.2021.17.09

摘 要 目的：构建一种能够较为准确地反映跨年度生存患者干预方案医保基金支出的计算方法，为医保预算影响分析（BIA）研究提供参考。方法：基于队列模型的生存率数据，以各年份中每个周期确诊的患者作为一个队列，计算各队列患者在研究年份内各状态下的人均生存周期数，即平均生存时间;在此基础上，再根据各队列的人数和各状态下的周期人均费用计算研究年份内所有队列的患者产生的总费用。以某癌症的干预方案作为示例，按所构建的计算方法进行演算，并将计算结果与目前几种常见算法结果进行比较;同时，对所构建的算法在特殊情形下的拓展情况提出应用建议。结果与结论：所构建的算法相比目前几种常见算法，其计算过程更符合真实世界中药物干预方案相关医保基金支出的过程，且其能够灵活适应多种特殊情形下的计算需求。该算法可较为准确地计算特定年份下某一干预方案的医保基金支出，在一定程度上解决了原有算法未充分考虑跨年度生存患者或计算过程简易、粗略而导致医保基金支出预测不准确的问题，可为我国医保BIA相关研究提供更准确的方法选择。

关键词 预算影响分析;跨年度生存;医保基金支出;计算方法;生存率

Calculation Method of Medical Insurance Fund Expenditure of Intervention Scheme for Cross-year Survival Patients Based on Survival Data of Cohort Model

HUANG Yuankai，CHEN Lei，LI Ying，XI Xiaoyu（The Research Center of National Drug Policy&Ecosystem， China Pharmaceutical University， Nanjing 211198， China）

ABSTRACT OBJECTIVE： To construct a calculation method which can accurately reflect the medical insurance fund expenditure of intervention scheme for cross-year survival patients， and to provide reference for the research of medical insurance budget impact analysis （BIA）. METHODS： Based on survival data of cohort model， taking the patients diagnosed in each cycle in each year as a cohort， the number of per capita survival cycle of cohort patients in each state in the study year was calculated， i.e. the average survival time; on this basis， the total cost of patients in all cohorts in the study year was calculated according to the number of people in each cohort and the per capita cost each cycle in each state. Taking the intervention scheme of a cancer as an example， the calculation was carried out by the established algorithm， and the calculation results were compared with the results of several common algorithms; at the same time， the application suggestions were put forward for the expansion of the constructed algorithm in special cases. RESULTS & CONCLUSIONS： Compared with the several common algorithms， the calculation process of the constructed algorithm is more in line with the process of medical insurance fund expenditure related to drug intervention scheme in the real world， and it can flexibly adapt to the calculation needs in a variety of special situations. This algorithm can more accurately calculate the medical insurance fund expenditure of a intervention scheme in a specific year， and to a certain extent solve the problem of inaccurate prediction of medical insurance fund expenditure due to insufficient consideration of cross-year survival patients or simple and rough calculation process. It can provide a more accurate method choice for the research of medical insurance BIA in China.

KEYWORDS Budget impact analysis; Cross-year survival; Medical insurance fund expenditure; Calculation method; Survival rate

药品的医保预算影响分析（budget impact analysis，BIA）可评价医保目录外药品进入医保目录对医保基金支出的影响，是药物经济学评价的重要补充。《2020年国家医保药品目录调整工作方案》要求在药品医保准入工作中，由地方医保部门和相关学术团体推荐医保管理、药物经济学等方面的专家组成评审专家，分为基金测算组和药物经济学组，分别从医保基金影响和药品经济学评价两方面针对谈判药品和竞价药品提出评估意见[1]，可见药品医保BIA日益受到我国医保部门的重视。

在药品医保BIA中，药品干预方案目标人群的确定是计算医保基金支出的重要环节，该目标人群指的是符合待评价干预方案的申请医保准入适用情形的所有患者[2]。长期疾病的患者可能在1年之后病情仍未进展而继续使用原干预方案，或生存期跨自然年，即可能存在跨年度生存患者，因此该类疾病的药品干预方案的目标人群不仅包括研究年份内的新确诊患者，也包括往年确诊且存活至研究年份的患者，而且不同时间段确诊的患者在研究年份内的平均生存时间很可能存在差异[3-4]。但是，目前关于跨年度生存患者在某一特定年份医保基金支出的计算方法尚未统一[5-7]，缺乏公认的计算方法，且有部分研究甚至未考虑跨年度生存患者所产生的医保基金支出情况[8-10]。

《中国药物经济学评价指南（2020中英双语版）》（以下简称“《指南》”）为药品医保BIA的框架构建提供了参考，但对于包括上述问题在内的BIA具体算法未提出详细指导意见[2]。因此，从理论角度而言，确定一种能较为准确反映跨年度生存患者在研究年份内医保基金支出的计算方法对《指南》的完善具有一定意义。就实践角度而言，考虑跨年度生存患者产生的医保基金支出能较为真实地反映干预措施的预期医保基金支出情况，有利于提高医保基金支出效率，促进我国医疗卫生资源的合理配置。

如果目标人群存在跨年度生存现象，无法准确计算年份内的平均生存时间，则可以考虑引入基于队列模型或基于个体模型的模拟方法来计算不同市场环境下目标人群大小的值[2]。因此，本研究基于队列模型，构建了一种根据队列的生存数据计算使用某一干预方案的跨年度生存人群在特定年份下平均生存时间的方法，再将该平均生存时间和单位时间的干预方案医保基金支出相乘，可以计算出该特定年份内的平均医保基金支出，然后再将其乘以干预方案的使用人数就可以得到该特定年份内干预方案的医保基金总支出;同时，本研究还以某癌症的干预方案为例，对本算法的计算过程进行基本演示，可得出本算法适用于存在跨年度生存的长期疾病患者的干预方案的医保基金支出计算。

1 平均生存时间计算原理

本算法与马尔可夫（Markov）模型、分区生存模型等药物经济学常用模型类似，可以考虑多种生存状态，且以循环周期为单位对状态的持续时间进行计算[11-12]。算法的基本理念是以各年份中每个周期确诊的患者作为一个队列，计算各队列患者在研究年份内各状态下的人均生存周期数，即平均生存时间;在此基础上，再根据各队列的人数和各状态下的周期人均费用计算研究年份内所有队列的患者产生的总费用。可见，患者在研究年份内各状态下的平均生存时间是本算法的关键内容。

本算法需要下列资料作为支撑：（1）从研究的干预方案上市年份至研究年份期间，研究疾病的发病人数资料——由于大多数流行病学资料仅能提供研究疾病的年发病率，故本研究将以各年份发病率为例进行阐述;（2）各年份发病人数中使用该干预方案的比例;（3）上述患者人群的长期随访生存率数据。

本算法有如下假设：（1）研究适应证下，同一年份内不同周期确诊的患者队列人数相等;（2）研究适应证下，确诊后使用相同干预方案的患者在各状态下各周期的生存率相同。

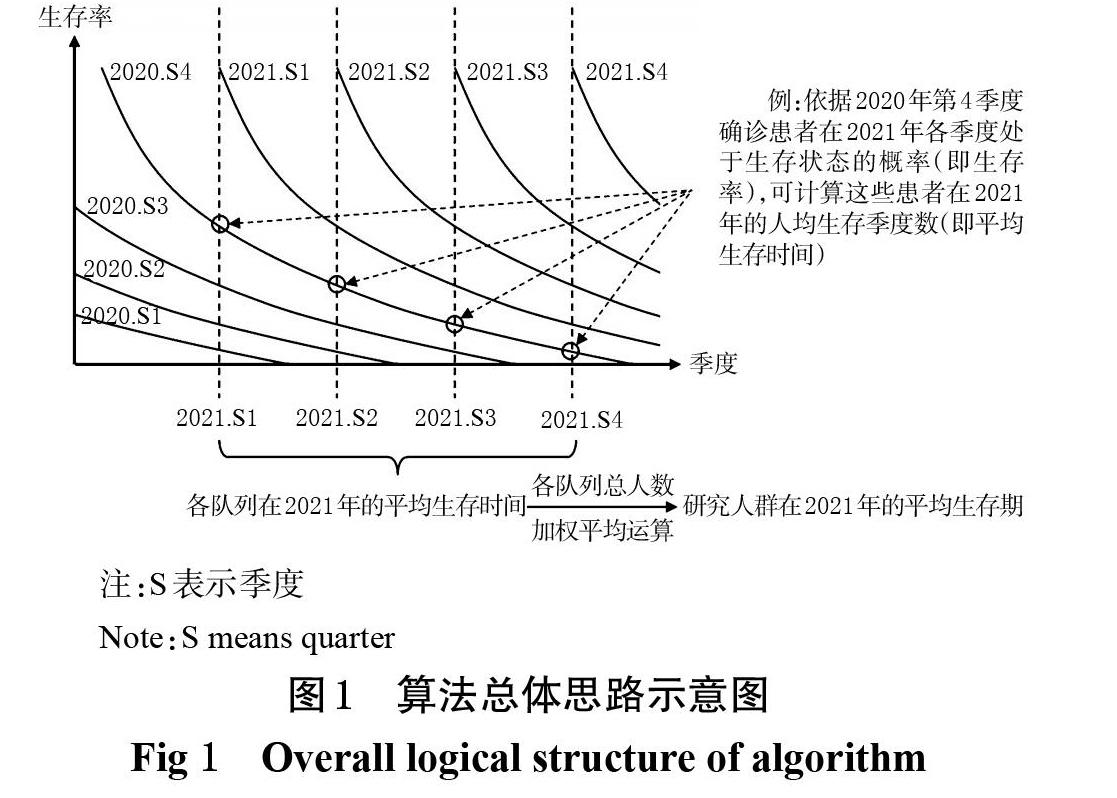
本算法的思路如图1所示。图中仅考虑生存和死亡2个状态，在时间轴上罗列某干预方案下各周期确诊的患者队列的生存率，并截取某特定年份内各周期（图1中以季度为周期）下各队列的生存率，将其视为该队列在该周期下的平均生存周期数，以此计算各队列在该年份下的平均生存时间（例如某队列患者在2021年第1季度的生存率是70%，则视为该队列在这个季度的平均生存时间是0.7个季度，后续3个季度以此类推;各季度下的平均生存时间相加即为该队列在2021年的平均生存时间），并按照各队列的总人数对各队列在该年份下的平均生存时间做加权求和计算，求得使用该干预方案的全部人群在该年份下的总生存期数（实际运算时，一般会先计算出各年份确诊患者队列在研究年份内的平均生存时间，然后用各年份发病人数中使用该干预方案的人数进行加权计算，而不是按照队列计算，因为按年份计算便于理解和编制BIA模型）。多状态模型在各状态下的平均生存时间计算思路亦同理。在此基础上，即可计算出使用該干预方案的人群在研究年份内的总生存周期数，进而计算出该干预方案在该年份的医保基金总支出。

2 平均生存时间和医保基金支出的计算方法

笔者现以“患者生存”这一单个状态为视角，基于患者的生存数据，阐述上述原理的详细计算方法如下。

2.1 定义基本信息和参数

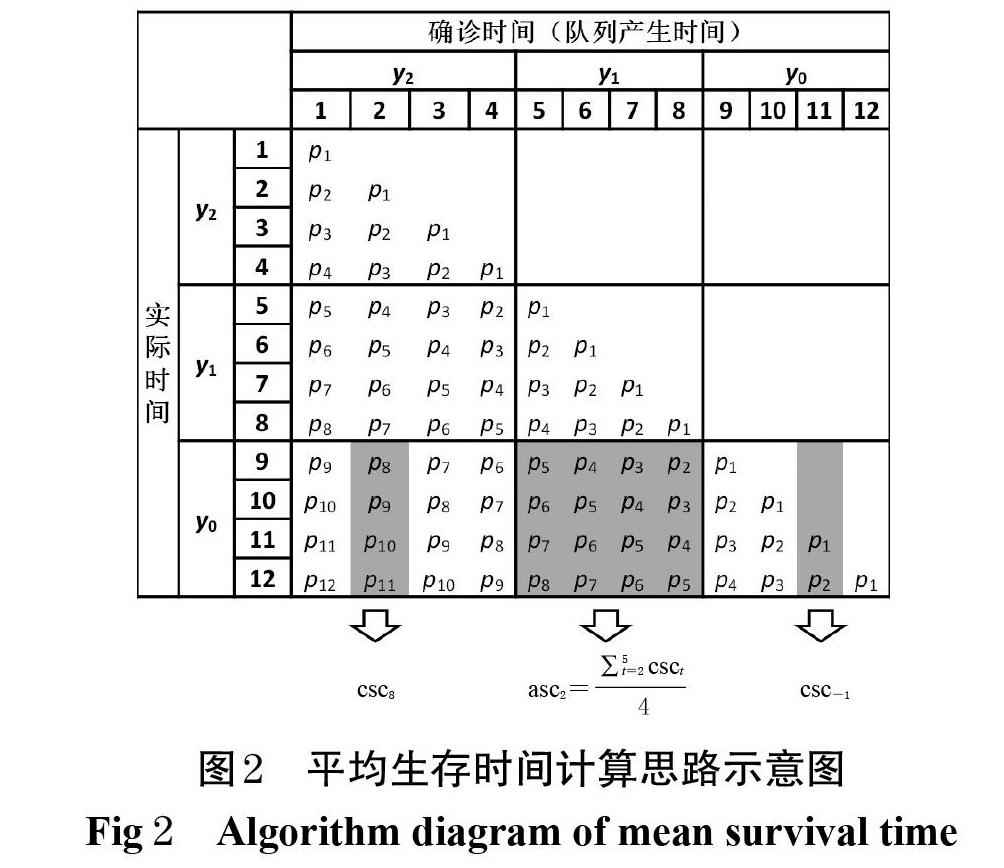
本算法的基本设定是：各年份内每个周期的确诊患者人数相等，且每个周期产生1个患者队列，并单独计算其生存情况。本算法同时使用2套时间系统，分别为患者的确诊时间和研究关注的时间段，两者均以周期为单位进行计算。以图2为例，各年份被平均划分为4个周期，各列分别为各周期确诊的患者队列的生存情况，各行分别为不同周期确诊的患者队列在实际时间中同一周期的生存情况。定义基线年（即研究的年份）为y0，基线年前一年为y0+1，以此类推从基线年开始向前n年（包括基线年）为yn，研究时间内生存队列最早产生的年份为ymax;pt为患者在干预方案下第t个周期的生存率，c为每年的周期数。图2中，y2为研究时间内生存队列最早产生的年份（ymax），c的取值为4。

2.2 计算某周期确诊患者在研究年份内的平均生存周期數

定义年内生存周期数（survival cycles of cohort，csct）为在某一周期确诊的患者队列从确诊第t周期开始1年内各周期的生存率的数值之和，其实际含义是接受该干预方案治疗的患者从第t周期开始1年内的平均生存周期数，计算公式为：

csct=pt+pt+1+pt+2+……+pt+c-1…（公式1）

在研究年份的csct中，t的取值为患者队列确诊周期开始到研究年份第1周期为止所经过的周期数。以图2为例，y2年第2周期确诊的患者在y0年第1周期时共生存了8个周期，所以其csct为csc8，其取值为第8、9、10和11周期的生存率的数值之和。

需要注意的是，为方便计算，csct中的周期数t可以取负值或0，且该2个取值下pt及其之后数个周期的生存率可能为0。以图2右下角为例，csc-1为p1和p2之和，即y0年第3周期确诊的患者在y0年的平均生存周期数在计算中依然视为其从y0年第1周期至第4周期的生存周期数之和，但因前2个周期中该队列患者尚未确诊，因此这2个周期的生存率视为0。

2.3 计算某年份确诊患者在研究年份内的平均生存周期数

定义单年产生队列年内平均生存周期数（average survival cycles of cohorts generated in one year，ascn）为yn年各周期确诊的患者在y0年的csct的均值，其实际含义是在假定yn年各周期确诊患者人数相等的情况下，yn年确诊的患者在y0年的平均生存周期数，计算公式为：

ascn=[∑c×（n-1）+1

t=c×（n-2）+2][csct][c] …（公式2）

公式2中的c可理解为yn年确诊的队列数量，则公式2的计算思路为yn年确诊的各队列在y0年的生存周期数之和除以yn年产生的队列数量，从而求得各队列的平均生存周期数。

以图2为例，y1年第1周期（周期5）确诊的患者在y0年各周期的生存率是患者确诊后第5～8周期的生存率，其总和为csc5;y1年第2、3、4周期确诊的患者以此类推，分别为csc4、csc3、csc2;这4个队列的生存周期数之和即为图中asc2对应的4个队列的cscn之和，将其除以y1年的确诊患者队列数4即为asc2。

2.4 计算干预方案全部使用人群在研究年份内的总生存周期数和年医保基金总支出

求得y0至ymax各年份确诊患者在y0年的平均生存周期数asc0、asc0+1……ascmax后，根据上述各年份使用该干预方案的人数对其做加权求和运算，即可得出使用该干预方案的人群在研究年份内的总生存周期数;再将其与该干预方案的单周期人均医保费用相乘，即可得出该干预方案的年医保基金总支出。

3 本研究算法的实例演算及与目前常见算法的比较

本研究以某癌症的干预方案为例，演算上述算法。该实例中，设定模型周期为1个月，则每年有12个周期。以2021年为研究年份，且该方案药物于2019年初上市，则生存队列从2019年1月开始，每月产生队列，直至2021年12月。假设使用该干预方案治疗的癌症患者队列的各周期无进展生存（progression-free survival，PFS）概率和总生存（overall survival，OS）概率符合Weibull分布，则用上述PFS期和OS期相关数据拟合PFS和OS曲线，并直接以各周期的时间中点作为周期数，以进行半周期校正，可得各周期PFS和OS状态下的生存率表达式分别为：Pt=e-0.06×（t-0.5）1.44、Pt=e-0.02×（t-0.5）1.41-e-0.06×（t-0.5）1.44;而各周期疾病进展（progressive disease，PD）概率为相应周期的OS概率减去PFS概率。

由于本实例从2019年1月确诊患者队列开始模拟，而研究年份为2021年，则2019年患者队列的平均生存周期数csct相对应的t值为2019年1月至2021年1月间的周期数（即25），其他队列以此类推，从而可用公式1计算出各队列在2021年的PFS期和PD期的csct;再据此计算2019、2020、2021年确诊患者在2021年的PFS期和PD期的ascn，结果如表1所示（表中2020年和2021年的部分计算细节略去）。

按照上述计算结果，可根据该干预方案的PFS期和PD期的单周期人均医保基金支出以及2019年至2021年各年份新确诊患者中使用该干预方案的人数，计算出2021年该干预方案产生的医保基金总支出。

本研究还将3种目前该领域的常见算法与本算法进行比较，结果如表2所示。表2中各算法分别为：（1）本研究构建的算法;（2）仅考虑2021年确诊患者在2021年产生的费用，按平均终生PFS期和终生PD期计算;（3）仅考虑2021年确诊患者产生的费用，按1月确诊后12个月（包括1月）的平均PFS期和PD期计算;（4）仅考虑2021年确诊患者产生的费用，按7月确诊后6个月（包括7月）的平均PFS期和PD期计算。各算法均使用上文计算实例中使用的生存数据来计算患者的PFS期和PD期，并假定2019年至2021年研究疾病的发病人数分别为10万人、11万人和12万人，以及该干预方案的PFS期费用为5 000元/月、PD期费用为2 000元/月。

由表2可见，如果医保BIA中的研究疾病和干预方案下存在跨年度生存的患者，目前常见的3种算法对干预方案在2021年产生的医保基金总支出的计算结果与本研究构建的算法结果比较差异较大，且大多低于本研究算法结果。从理论上讲，相比目前常见算法，本研究算法能够对BIA目标人群在研究年份的生存情况进行较为贴近现实的模拟测算，因而能够为医保BIA提供更为准确的人均生存或用药时长参数。

4 讨论

本研究基于患者生存率构建了一种针对跨年度生存患者的医保基金支出的计算方法，相比目前该领域中常见的算法，本算法可较为准确地计算特定年份下某一干预方案的医保基金支出，在一定程度上解决了常见算法未充分考虑跨年度生存患者或计算过程简易、粗略而导致医保基金支出预测不准确的问题，可为我国医保BIA相关研究以及《指南》的完善提供参考，为研究者和决策者提供建议，促进我国医疗卫生资源的合理配置。

4.1 本算法关键问题的解释

首先，本算法在构建过程中引入了某周期确诊患者在研究年份内的平均生存周期数csct和某年份确诊患者在研究年份内的平均生存周期数ascn这2个概念以便于计算，其实际意义理解起来较为晦涩，但其基本含义均是指某一时间段内确诊的患者在研究年份或研究年份内某一周期的平均生存时间。需要注意的是，这与传统意义上的患者平均生存时间（患者从确诊或开始干预直至死亡的时间跨度）的概念有所差异。

其次，本研究引入了负生存周期数的概念（公式1），该设计并无实际含义，仅为方便统一和简化公式而设计，因而无需从现实意义角度进行理解。

第三，本算法可基于多状态模型计算，其计算思路与上文中所述单个状态的计算思路完全一致。例如在“3”项下实例中，本研究以存在PFS和PD 2个健康状态的癌症为例计算了各状态下的患者平均生存时间。

4.2 本算法的使用条件和关键设置

因为本算法是基于患者生存率构建的，因此使用本算法的基本条件是可以获得符合研究需求的生存数据;同时，为计算研究年份内的医保基金支出，需要获取干预方案在各年份新确诊患者中的使用人数，该参数可通过专家咨询、临床调研等方式获得。

在将本算法应用到医保BIA的过程中，有2个关键参数需要进行设置：1）研究范围内生存队列的最早产生年份ymax，可以通过设置模型模拟结束的生存率阈值来确定，且要注意该值必须为整数;2）每年的周期数，可以根据疾病特征来设计，但为方便计算，须尽量使每年周期数为整数。

4.3 特殊情形下本算法的拓展

由于实际市场和临床情况比较复杂，上述算法需根据实際用药情况灵活改变，以下列举了本算法在一些特殊情形下的拓展情况。

4.3.1 新药上市或适应证获批时间晚于理论上的ymax 对于一些新药或获批新适应证的药品，在进行医保BIA过程中，若按照生存率阈值确定ymax，则可能出现新药上市年份或新适应证获批年份晚于ymax的情况，此时计算所得的医保基金支出有悖于实际情况。

因此，对于新药或新获批适应证的药品，ymax的设计应考虑药品上市或适应证获批的年份——若新药上市或新适应证获批的年份早于理论上的ymax，则按照生存率阈值确定ymax;若新药上市或新适应证获批的年份晚于理论上的ymax，则以新药上市或新适应证获批年份作为ymax。在实际中，新药上市时间或适应证获批时间可能在年末，导致该年的销售量较低，此时可根据药品销售情况调整算式中的起始年份为药品上市或适应证获批年份的后一年，或仅将获批年份下产生的队列作为该年度的全部患者队列来计算ascn。

4.3.2 治疗过程中仅接受干预方案的一次性治疗 在部分研究中，可能会出现患者仅接受该研究关注的干预方案的一次性治疗，后续治疗周期中接受其他干预方案治疗的情况[13]。该情况下，由于对医保基金产生影响的变动仅发生在研究关注的年份内，故ymax可直接设置为研究关注的多个年份中最早的一年。例如癌症放疗方案的BIA中，一般假设干预方案本身的费用在患者确诊周期已全部发生，但后续的患者生存情况会因选用不同的放疗技术而存在差异。在这样的情况下，实际上干预方案调入或调出报销范围对该方案选择的影响仅出现在报销范围调整生效后的年份，因此仅需计算报销范围调整后年份的人均生存或用药时间。

4.3.3 实际用药时长与理论时长有差异 这类情形主要分为2种：①患者中止治疗。本算法中所使用的生存数据来源于临床试验和已公开发表的文献，研究对象在用药时应处于严格的临床试验条件下或其用药依从性高，其生存数据反映了患者用药后理想的生存情况。但在实际治疗过程中，用药依从性较差、药物可及性较低等原因可导致患者突然停止治疗[14]，此时若仍使用文献报道的生存数据可导致生存率虚高。在该情况下，应考虑将ymax设置为绝大部分患者的最长用药时长，例如发现研究对象中95%的患者都会在2.5年内因依从性差而停止用药，但理论上的ymax为5年，则ymax实际应设置为3年。此处建议不以患者的平均用药时长来估算ymax，否则会导致部分患者在超过该时长后的用药被忽略，继而低估医保基金支出。②患者停止用药后，该研究所关注的干预方案的药效仍持续了一段时间。生存率反映的是干预方案的临床治疗效果，但某些长期疾病的患者在停止用药后，之前服用的药物仍可维持病情的稳定，此时基于生存率计算而得到的平均生存时间并不等于实际用药时间，导致医保基金支出预测不准确。在该情况下，可设置用药时长阈值，或根据实际用药时长设置生存率阈值，使计算而得的患者队列的平均用药时长接近实际用药时长。

4.3.4 年份内各周期确诊人数存在明显差异 在常见的流行病学资料中，研究者往往仅能获得疾病的年发病率数据，而没有各周期的发病率数据。本研究为贴近实际，且为方便解释计算原理，故假设一年中各周期的发病率相等。但在实际研究过程中，研究者也许能够获得或计算出更为详尽的发病率数据，这种情况下，可以为模型中每个队列单独赋予确诊人数，并单独计算每个队列的生存时间，以更充分地利用高质量的发病率数据。

4.3.5 新确诊患者和跨年度生存患者的费用结构存在差异 部分研究中，新确诊患者与跨年度生存患者的年均总费用构成可能存在差异。例如放疗、手术等干预方案成本在BIA中一般仅会被纳入新确诊患者的费用构成中。对此，可以分开计算本年度新确诊患者队列和跨年度生存患者队列的年均总费用，为本年度新确诊患者单独增加成本项目。

4.4 局限性

本研究构建的算法存在一定局限性：第一，本研究构建的算法需要使用该干预方案的患者的生存数据和各年份使用该干预方案的患者人数，如果这2项数据无法获取，则无法使用本算法;第二，由于实际中难以追溯年份内不同周期确诊的患者人数，而本算法假设不同周期确诊的患者人数相等，因此计算得到的平均生存率可能与实际存在一定偏差;第三，由于医保BIA关注的实际市场情况和临床情况复杂，而本算法尚未经过大量研究的应用和实证，因此本研究对一部分特殊情形下算法的拓展提出了建议，但在研究一些具体BIA问题时，本算法的适用性仍可能较低，有待继续改进或开发更为合理的计算方法。

5 结语

长期疾病药物干预方案的医保BIA中，目前常见的计算方法常未考虑跨年度生存的患者群体，或计算方法较为粗略，对医保基金支出估算的准确性产生了影响。本研究以完善医保BIA建模思路为目的，基于患者生存率构建了一种存在跨年度生存患者情形下的医保基金支出计算方法。本方法的基本思路是计算研究年份及其以往各年份内使用某干预方案（如药物治疗方案）的确诊患者在研究年份内的平均生存周期数，再根据各年份的确诊患者中使用该干预方案的人数和人均周期成本计算该干预方案在研究年份的总医保基金支出。本算法能够在一定程度上解决目前常见计算方法中对跨年度生存情形下的医保基金支出预测不准确的问题。但由于实际市场情况和临床情况复杂，本算法需根据实际用药情况灵活改变。

参考文献

[ 1 ] 国家医疗保障局. 2020年国家医保药品目录调整工作方案[EB/OL].（2020-08-17）[2021-08-06].http：//www.nhsa.gov.cn/art/2020/8/17/art_37_3407.html.

[ 2 ] 刘国恩.中国药物经济学评价指南：2020中英双语版[M]. 北京：中国市场出版社，2020：91-92.

[ 3 ] WU Y L，CHU D T，HAN B，et al. Phase Ⅲ，randomized，open-label，first-line study in Asia of gefitinib versus carboplatin/paclitaxel in clinically selected patients with advanced non-small-cell lung cancer：evaluation of patients recruited from mainland China[J]. Asia Pac J Clin Oncol，2012，8（3）：232-243.

[ 4 ] MOVAHEDI M，HEPWORTH E，Mirza R，et al. Discontinuation of biologic therapy due to lack/loss of response and adverse events is similar between TNFi and non-TNFi class：results from a real-world rheumatoid arthritis cohort[J]. Semin Arthritis Rheum，2020，50（5）：915-922.

[ 5 ] 謝丽，夏茹意，庄贵华.伴代偿期肝硬化乙肝相关肝癌患者根治性切除术后抗病毒治疗的预算影响分析[J].中国卫生经济，2019，38（9）：64-68.

[ 6 ] 殷潇，方欣，胡江蔺，等.舒尼替尼治疗转移性肾细胞癌的预算影响分析[J].中国卫生经济，2016，35（12）：67-69.

[ 7 ] 张欲晓，殷潇，田梦媛，等.赫赛汀治疗HER-2阳性乳腺癌的医保预算影响分析[J].中国卫生经济，2016，35（12）：63-66.

[ 8 ] 陈斌斌，范长生.注射用紫杉醇（白蛋白结合型）治疗晚期乳腺癌的预算影响分析[J].中国医疗保险，2016（12）：60-63.

[ 9 ] 范长生，何敏媚，吴久鸿.复方黄黛片治疗急性早幼粒细胞白血病预算影响分析[J].中国新药杂志，2017，26（10）：1219-1224.

[10] 张强，崔颖，马锐，等.规范使用唑来膦酸治疗国内晚期肺癌或乳腺癌合并骨转移预算影响分析[J].中国医疗保险，2018（12）：59-67.

[11] 张洁，黄泰康. 药物经济学评价中马尔可夫模型的优化：马尔可夫决策模型[J].中国药房，2008，19（17）：1284- 1286.

[12] 邵荣杰，唐文熙，马爱霞.分区生存模型在药物经济学评价中的应用[J].中国卫生经济，2019，38（9）：60-63.

[13] 汪红艳，孔令玲，王凡，等.老年食管癌放射治疗疗效及预后影响因素分析[J].安徽医科大学学报，2016，51（8）：1188-1192.

[14] 洪梅花，徐东晓，童素梅，等.急性心肌梗死支架术后患者不同时期服药依从性及其影响因素的调查与分析[J].中国护理管理，2014，14（12）：1261-1265.

（收稿日期：2021-01-27 修回日期：2021-08-06）

（编辑：胡晓霖）