液滴在球面的钉扎：宏观前进与后退角的预测模型

林昌盛，朱张磊，印万忠1,，姜又华

（1.福州大学，福州 350108；2.广东以色列理工学院，广东 汕头 515063；3.东北大学，沈阳 110819）

润湿是最基本的物理现象之一[1]，在传热传质、微流体及矿物浮选等领域有着十分重要的应用价值[2-7]。液滴在固体表面的钉扎是润湿现象中最重要的特征之一，而钉扎程度一般由接触角表征[8]。接触角是气液界面与固液界面的夹角[9]，包括前进接触角θa与后退接触角θr，即分别为接触线向前扩张与向后收缩之前的接触角，两者之差被称为滞后接触角（也即接触角迟滞现象），是表征液滴钉扎程度的重要参数[10]。目前，关于液滴前进与后退接触角的工作大多在二维平面，例如研究基底微结构对液滴钉扎特征的影响机理等[11-13]。

然而，许多涉及到液滴钉扎的应用都离不开球面，例如浮选中矿物颗粒的表面。目前已有一些针对液滴在球面（或者曲面）润湿现象的研究[14-18]。Jasper等[14]采用广义变分法建立预测纳米液滴在曲面的接触角模型，并利用壬烷、十二烷、富勒烯等有机物作为液滴，成功地证实接触角模型的适用性。Viswanadam等[16]将接触角与曲率半径和液滴体积相结合，得出相应的模型，并利用试验数据来验证该模型。Wu 等[17]建立了预测液滴在曲面的宏观接触角模型，并考察了曲率半径以及固体表面的润湿性对宏观接触角的影响程度。然而，研究液滴在球面上前进与后退时的钉扎特征的工作较少。对于在球面上的液滴，其接触角较难测得（因为这需要明确气液界面切线与固液界面切线的夹角，其中固液界面的切线极难准确地观测，如图1b 所示），而在三相接触线处的气液界面切线与三相接触线所在平面形成的宏观角（如图1a 所示的θH）较易得到相对准确的值。更为重要的是，液滴的受力特征，如气液界面张力的方向，由宏观角θH决定[18]。因此，应利用液滴在球面的宏观前进与后退角来研究液滴在曲面上的钉扎特征，但目前关于曲率半径对液滴宏观前进角θHa与后退角θHr的影响机制还未明确。

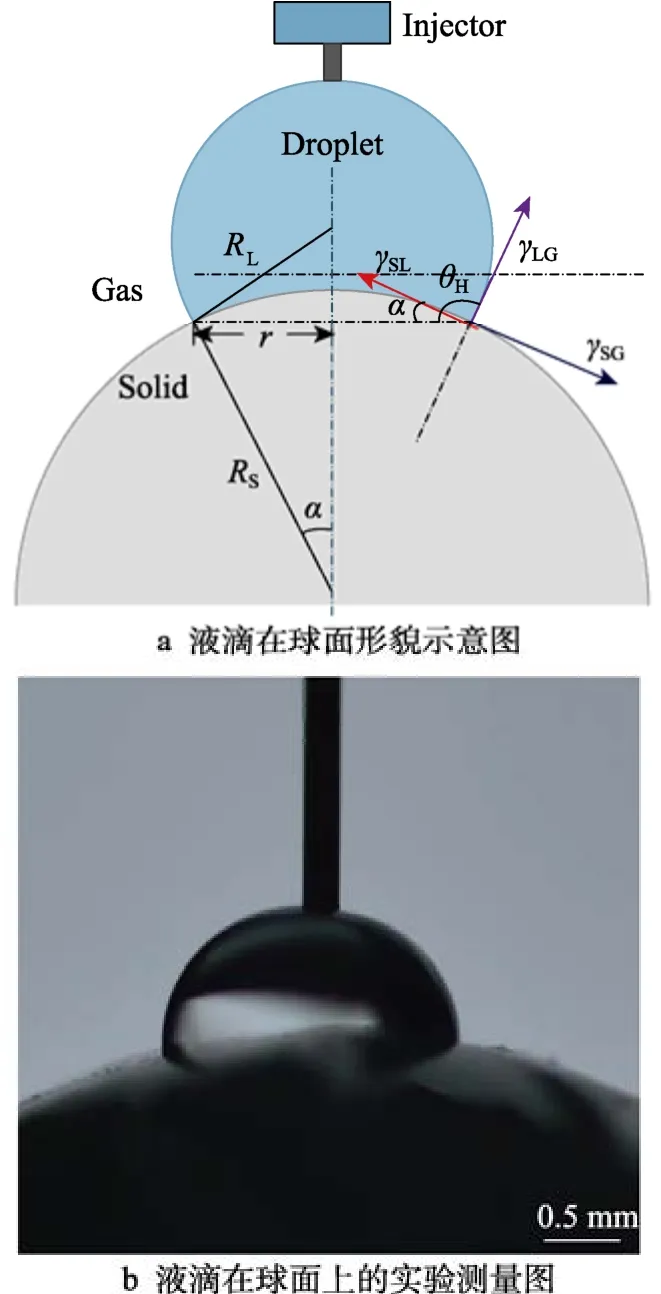
图1 液滴在球面的形貌示意图及液滴在球面上的实验测量图Fig.1 a) Schematic diagram of a droplet on a spherical surface, b)Experimental diagram of a droplet wetting a spherical surface

本工作基于液滴在球面钉扎时的吉布斯自由能与体积公式，得到吉布斯自由能、液滴体积、球面曲率半径、接触角和宏观角之间的关系。其次，把介观接触线钉扎的能量引入体系吉布斯自由能，并依据液滴在吉布斯自由能最小时呈现出宏观前进角θHa与后退角θHr的现象，利用液滴的本征前进接触角θa与后退接触角θr预测液滴在球面的θHa与θHr，并讨论曲率半径对宏观角的影响机制。最后，利用测得的宏观角数据验证所预测的模型。

1 试验

如图1 所示，试验通过座滴法测量去离子水液滴在球面上的宏观前进角θHa和后退角θHr。球面是由PET（聚对苯二甲酸乙二醇酯）膜包覆的玻璃珠（半径分别为2、4、6、8 mm）。首先，通过微型注射器在球面上生成一个体积约为3.0 μL（VL）的液滴；然后，利用注射泵以0.04 μL/s 的速度向液滴内部添加或吸取去离子水，当三相接触线出现明显移动之前所观测到的宏观角θH即为宏观前进θHa或后退角θHr。本研究所得的数据是至少5 次试验的平均值。

2 结果与分析

2.1 试验结果

如表1 所示，测得液滴在二维PET 平面上的本征前进角θa与后退接触角θr分别为(91±2)°与(55±3)°。试验测得的液滴在不同曲率半径球面上的宏观前进角θHa和后退角θHr均随着曲率半径RS的增大而减小，并分别趋近于θa与θr。

表1 液滴在不同曲率半径球面的宏观前进角和后退角Tab.1 Values of droplet apparent angles on spherical surfaces with different curvatures

2.2 结果分析

图2 基底表面上液滴的前进接触角与后退接触角示意图Fig.2 Schematic diagram of the advancing contact angle (a) and the receding contact angle of a droplet on a realistic flat surface (b)

式中：RS、VL和θ（θa或θr）为已知量，G*、α和θH（θHa或θHr）为未知变量。依据公式（7）和公式（9）可知，存在无数组α和θH的组合及相对应的G*值，且其中必定出现使G*值最小的α和θH组合。

图3 球缺液滴示意图（其中黑色曲面与红色曲面之间的体积为VL，黄色平面与红色曲面之间的球缺体积为V，VL+V 即黑色曲面与黄色平面之间的球缺体积）Fig.3 Schematic diagram of a spherical cap, where VL represents the volume between the black and red curved surfaces, V represents the volume between the yellow plane and the red curved surface, and VL+ V represents the volume between the black curved surface and the yellow plane

如图4 所示，以满足公式（7）与公式（9）为前提，在不同曲率半径条件下，G*值随着θH−α（即液滴在球面上的接触角）变化的情况。从图4 中可知，不论曲率半径为何值，G*值最小时所对应的θHa−α（或θHr−α）值与液滴在平面上的本征前进接触角θa（或后退接触角θr）的大小相等。这表明在考虑介观接触线钉扎最大能量的前提下，当体系吉布斯自由能最小时，液滴在球面上的接触线处于即将前进或后退的状态，此时相对应的宏观角即为宏观前进角θHa或后退角θHr。体系吉布斯自由能最小意味着体系处于最稳态[19]，因此若将接触线的最大钉扎能量纳入体系吉布斯自由能时，液滴的前进或后退接触角出现于体系最稳状态下。此外，图4 还具有更为重要的实际意义，即基于公式（7）与公式（9）并使G*最小时，可直接预测液滴在球面上的宏观前进角θHa与后退角θHr。

图4 在不同曲率半径条件下G*随θHr−α 变化的情况和G*随θHa−α 变化的情况Fig.4 Diagrams of the value of G* with respect to θHr−α (a) and the value of G* with respect to θHa−α for surfaces with different curvatures (b)

图5 显示了在满足公式（7）与公式（9）的条件下，当体系吉布斯自由能最小时，不同曲率半径的球面基底上液滴宏观前进角与后退角的预测情况。从图5 中可知，随着曲率半径的增大，G*的最小值减小，且G*值最小时所对应的θHa或θHr也减小。此外，依据上述推导的球面体系吉布斯自由能公式，同理可得，液滴在二维平面上，其前进或后退接触线处于最大钉扎状态时，无量纲化的体系自由能公式为：

其中θH为液滴在平面上的宏观角，θ为测得的液滴在基底上的本征前进或后退接触角[8,20]。因此，如图5 所示，当曲率半径为无穷大时，即球面成为二维平面时，液滴的宏观前进角或后退角的大小等于本征前进接触角θa（91°）或后退接触角θr（55°）。

图5 在不同曲率半径条件下G*随θHr 和θHa 变化的情况（其中箭头代表G*的最小值）Fig.5 Diagrams of the value of G* with respect to θHr (a) and the value of G* with respect to θHa (b) for surfaces with different curvatures, where the arrow indicates the minimum of G*

图6 展示了在不同曲率半径的球面基底上，预测所得宏观角（虚线）与试验测得数据（已在表1 列出）的对比。可知，试验值与预测值（宏观前进角和后退角）随着曲率半径变化的趋势一致，但宏观后退角的试验值普遍略小于预测值，这可能是因为在试验中注射器的存在，使得液滴的形貌偏离球缺状。总而言之，试验测得的液滴在球面上的宏观前进角和后退角与预测的数据大体上相吻合，这表明本研究所建立的宏观角预测模型的可行性。

图6 在不同曲率半径的球面基底上预测和试验所得的θHa和θHr 的对比Fig.6 The comparison of predicted and measured θHa and θHr on spherical surfaces with different curvatures

3 结语

与以往大多在二维基底的研究不同，本工作瞄准球面上液滴钉扎的问题，建立了液滴在球面上的宏观前进角与后退角预测模型，并讨论曲率半径对体系吉布斯自由能以及宏观角的影响机制。由于不存在绝对光滑的表面，故将介观接触线的钉扎能量纳入即将移动液滴的吉布斯自由能内，且接触线最大钉扎所产生的能量被假想为势能。基于液滴在球面上的吉布斯自由能与体积表达式，即公式（7）和公式（9），得出球面曲率半径、液滴体积、本征接触角与宏观角之间的关系式。依据吉布斯自由能最小时液滴呈现出宏观前进角与后退角的发现，利用已知的本征前进与后退接触角预测液滴在球面上所对应的宏观前进角和后退角，且所预测的结果被试验测得的数据证实。所得主要结论如下：

1）随着球面曲率半径的增大，体系吉布斯自由能减小，且最后趋近于液滴在二维平面上的自由能。这表明越弯曲的表面，越易于让液滴处于不稳定状态。

2）液滴的宏观前进角θHa和后退角θHr随曲率半径的增大而减小。这意味着表面曲率半径的减小，可增大液滴的宏观角。

3）在一定误差范围内，当表面的本征前进与后退接触角、液滴体积、曲率半径已知时，液滴在球面上的宏观前进角与后退角可以被成功地预测。

本研究建立了液滴在球面的宏观前进角与后退角预测模型，这在一定程度上丰富了润湿理论的内容，但其中仍存在一些不足之处，例如试验所采用的液滴仅仅是纯溶剂（去离子水），固体曲面仅包覆亲水性材料膜（PET 膜），且固体曲面是对称的。但在实际应用中，例如浮选领域，液滴一般是混合表面活性剂或是含有微纳米颗粒的混合表面活性剂，而固体表面则可能具有疏水性，且存在微纳结构或不均匀的化学基团[21-28]。因此，需要进一步研究更复杂的体系，创建出适合实际应用的理论公式或模型，以期更好地为工业应用提供指导。