基于数据驱动的晶体直径模型辨识方法研究

张西亚,高德东,王 珊,林光伟,高俊伟

(1.青海大学机械工程学院，西宁 810016； 2.阳光能源(青海)有限公司，西宁 810000)

0 引 言

在直拉硅单晶生长过程中，等径阶段的硅单晶是后期加工利用的有效部分。在这个阶段，稳定的直径控制可以有效减少晶体缺陷的产生，并且可以减少后续加工的浪费[1]。目前，直拉硅单晶的直径控制主要有PID控制和基于模型控制两种，其中PID控制有基于称重的PID控制方法和基于光学测径的PID控制方法[2-3]，但是传统的PID控制方法存在调节时间长、控制精度低、参数整定复杂和控制回路抗干扰能力差等问题，并且难以适应高质量、大尺寸单晶的生长要求[4]。随着控制理论的迅速发展，许多学者提出了基于模型的控制方法应用在单晶硅生长过程控制中。基于模型的控制方法控制精度高，可以满足晶体质量的低缺陷指标，是生长高质量大尺寸单晶的有效策略[5]。因此，基于模型的控制方法已成为直拉单晶硅控制方法研究的主要方向。

基于直拉法硅单晶生长的建模方法有数据驱动建模和机理建模两类。其中，机理建模是依据单晶硅生长系统的内部机理建立数学模型，Zheng等[6]建立了以提拉速度和加热器功率为输入，晶体生长速度和晶体半径为输出的集中参数模型。王海龙[7]使用子空间辨识算法来获得等径阶段的分段热场温度模型，并利用改良的贝叶斯概率加权多模型预测控制策略控制整个拉晶过程的热场温度；梁炎明等[8]利用T-S模糊模型获得了直拉硅单晶晶体直径、提拉速度和热场温度之间的集总参数数据模型，并在集总参数数据模型的基础上，使用模型预测控制算法对晶体直径进行控制；Rahmanpour等[9-10]根据生长界面热量变化和弯月面几何关系，建立了输入为加热器功率和提拉速度，输出为熔体温度和半径的非线性状态空间模型；Winkler等[11]基于能量守恒和流体动力学等理论，建立了Cz硅晶体生长过程的机理模型。张诚[12]在温度串级和提拉速度控制系统的基础上，利用时变参考轨迹的动态矩阵和史密斯预估器控制算法控制晶体直径。虽然上述基于机理建模的控制方法具有较高的控制精度，但建立高精度的晶体直径数学模型是实现其精确控制的前提条件[13]，且Cz硅单晶的非线性、大时滞等特性仍然是影响其控制精度的主要原因。

数据驱动建模[14-16]是根据拉晶过程中实测的输入、输出数据，提取出其内包含的深层次有效信息，进行参数估计、过程辨识后得到的模型。梁炎明等[17]研究了T-S模糊自组织算法，选取晶体硅生长过程中热场温度和加热器功率的特定数据段，并使用所研究的算法识别出热场温度和加热器功率之间的非线性模型；Shah等[18]用自回归滑动平均数据模型描述晶体生长过程，与机理模型相比，此方法更加简单，更适合于实际控制；严博涛[19]采用最小二乘法及其变形算法对单晶硅直径与加热器温度之间的阶跃响应模型参数进行了辨识；景坤雷[20]根据改进的蚁狮算法构建了硅单晶等径阶段热场温度与加热器功率之间的非线性动态模型，该方法考虑了硅单晶生长过程的特点，建立了分段等径阶段的模型，并成功地将所建立的模型应用于热场温度控制。但以上基于数据驱动建模的控制方法都使用单一因素控制，忽略了晶体生长过程中其他主要参数对晶体直径的影响，以及其他主要参数随时间缓慢变化的问题只适用于生长过程中的特定阶段。因此，本文提出一种多输入、单输出的BP(back propagation)神经网络晶体直径辨识模型，以用于直拉单晶硅生长过程中单晶硅棒直径的预测，以期能够为晶体直径的控制提供一种更为精确的晶体直径辨识模型。

1 关联性分析及特征量化

1.1 关联性分析

在直拉硅单晶生长过程中，单晶硅生产条件比较复杂，需要大量的传感器来监测单晶炉的环境参数，每次拉晶都将产生大量的生产数据,如若能够提取出其内包含的深层次有效信息,必将大幅提高晶体直径控制精度,进一步提高晶体质量。由于所能测量的拉晶参数较多，而以与晶体直径相关度高的参数作为特征值必定能够提高神经网络的训练效率与准确性,故先利用关联性分析寻找最佳特征值。

采用相关分析法对晶体直径与各拉晶参数之间的关联性进行定量计算。相关分析是研究两个或多个变量之间的相关程度，并用一定的函数表示这种关系的一种方法。相关变量间不存在确定性关系，一般使用相关系数R来表示两个变量间的密切程度，R的绝对值越接近于1表示相关性越好，计算公式为：

(1)

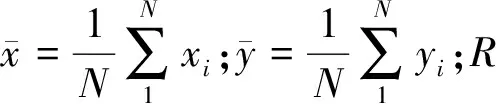
表1 晶体直径与各拉晶参数的相关系数Table 1 Correlation coefficient of crystal diameter and each crystal pulling parameter

由表1可以看出21个拉晶参数与晶体直径的相关系数，线性相关按强弱程度可划分为三级：

|R|<0.4为低度线性相关；0.4<|R|<0.7为显著性相关；0.7<|R|<1为高度线性相关。本文为了提高神经网络的训练效率与准确性，将与晶体直径呈高度线性相关的12个拉晶参数作为特征值，用以训练神经网络。神经网络训练所使用的特征值如表2所示。

表2 神经网络训练所使用的特征值Table 2 Feature values used in neural network training

1.2 特征值归一化

由于12个特征值的单位不同，且数量级不统一，若将所采集获得的拉晶参数样本数据直接输入BP预测算法会降低晶体直径预测的准确性和算法的收敛性，直接降低算法的效率。因此，必须对所采集的样本数据进行单位和数量级上的预处理，使12个特征值在数量级和单位上达到一致。本文采用数据归一化进行各参量的单位和数量级的统一，数据归一化是一种最简单实用的归一化方法，通过数据归一化可以很好地统一12个参量的单位和数量级，其计算公式为：

(2)

式中：Xn为原始参量数据;Xmax、Xmin分别为原始参量数据中最大值和最小值；Pn是归一化后的参数数值。在利用BP预测算法进行训练和测试时，必须使用相同最大值和最小值。

2 晶体直径预测模型

2.1 预测模型的工作流程

基于神经网络的晶体直径预测模型的工作流程如图1所示，具体分为三大模块:数据准备、网络训练和网络计算。其中，数据准备主要是获取单晶硅生产车间里的CL120-97单晶炉拉晶数据，对拉晶数据进行分析处理确定神经网络的输入和输出，并将拉晶数据分为训练数据以及验证数据，为神经网络的训练做准备；网络训练主要是通过确定神经网络的输入、输出、隐藏层数、隐藏层节点数和训练函数，来构建神经网络的拓扑结构，通过训练函数调整神经网络各层间的权系数，权系数w能够反映训练过程中输入和输出之间的映射关系，训练后即可得到满足精度要求的神经网络；网络计算主要是将拉晶数据作为训练后神经网络的输入，经神经网络计算后得到晶体直径，实现对晶体直径的预测。具体流程如图1所示。

图1 晶体直径预测模型工作流程图Fig.1 Work flow chart of crystal diameter prediction model

2.2 神经网络搭建

本文用归一化之后的特征值组成的12元组Xi=(X1,X2,X3,…,X11,X12)作为BP神经网络输入，使用晶体直径Yi作为BP神经网络输出。

三层神经网络模型能够很好地解决一般的函数拟合和逼近问题，其网络拓扑一般由输入层、隐藏层和输出层组成[21]。当神经网络的隐藏层数为1层时，神经网络可以逼近任意连续函数，而增加神经网络的隐藏层个数有利于模型预测精度的提升，综合考虑模型精度及复杂程度，选取隐藏层为2层的神经网络。

对于隐藏层节点的选择，假如在设计神经网络的过程中，隐藏层神经元的节点数较多，则容易导致数据过度拟合，使模型所提取的特征值缺乏代表性，反之，如果隐藏层神经元节点数过少，则容易导致神经网络的学习能力较弱，使模型所提取的特征值表达能力较低。因此，在本文的实验中，借鉴其他设定经验，同时使用主观设定法去尝试隐藏层的节点数，其中隐藏层节点数设置的参考公式为:

(3)

式中：m表示隐藏层的节点数；n表示输入层中神经元的节点数；l表示输出层中神经元的节点数；a是介于[1,10]之间的常数。

根据公式(3)可以计算出隐藏层神经元数的取值范围为[4,13]，隐藏层神经元数目在[4,13]范围内的平均相对误差，可以通过逐渐增加隐藏层神经元数目并试算后得到，如图2所示。由图2可以看出，当隐藏层中神经元数为10时，预测值与测试值之间的平均相对误差(ARE)最小。因此，隐藏层神经元数取10。

图2 不同神经元数和平均相对误差的关系Fig.2 Relationship between the number of different neurons and the average relative error

以Sigmoid型函数中的Logistic函数作为神经网络隐藏层神经元传递函数，以线性传递函数purelin作为输出层中神经元的传递函数，以Levenberg-Marquardt算法的训练函数trainlm作为训练函数[22]。设定神经网络的参数后，即可得到硅单晶直径预测模型的BP神经网络拓扑结构，如图3所示。

图3 神经网络拓扑结构Fig.3 Neural network topology diagram

2.3 BP神经网络训练

根据以上输入输出形式，将在单晶硅生产车间采集的CL120-97单晶炉拉晶数据，分为训练数据和验证数据。训练数据(占总量90%以上)用于训练神经网络，验证数据用于验证训练后的神经网络预测模型的准确性。图4为验证数据经神经网络预测模型计算后所得结果图，结合图4(a)和4(b)可以看出该模型对前80个直径样本的预测具有很高的准确性，其后样本的直径预测效果相对较差，200个直径样本预测的平均相对百分比误差为0.140 94%。

图4 BP神经网络晶体直径预测结果。(a)预测值与真实值的对比；(b)预测值与真实的平均相对误差Fig.4 Crystal diameter prediction results of BP neural network. (a) Comparison between predictive value and actual value; (b) average relative error between predictive value and actual value

BP神经网络算法[23]虽然具有较强的局部搜索能力，但其预测结果还取决于神经网络的原始状态，容易陷入局部最小值，降低对晶体直径的预测精度。因此，本文使用擅长全局搜索的遗传算法(genetic algorithm，GA)优化BP神经网络的权值和阈值[24-25]，并在众多解空间中找到最佳的搜索空间，然后使用BP算法在此解空间中搜索最优解，实现对直拉硅晶体直径的精确预测。

3 遗传算法优化直径预测模型

3.1 遗传算法优化预测模型的算法流程

遗传算法是借鉴生物界优胜劣汰、适者生存的进化规律演变而来的启发式随机搜索算法，具有良好的隐并行性和全局寻优能力，其学习近似最优解不需要误差函数的梯度信息，它适用于求解复杂的非线性问题。遗传算法包括编码、适应度函数计算、种群初始化、复制、交叉和变异，本文将遗传算法与BP神经网络算法相结合，将BP神经网络隐藏层节点的阈值和权值作为遗传算法的输入信息，并对其进行编码生成种群，然后利用遗传算法的复制、交叉和变异算子生成新的子代，作为BP神经网络算法进行网络训练的初值，随后用遗传算法检验个体是否达到适应度标准，不达标的个体进行复制、交叉和变异操作，直到个体满足精度要求或适应度标准为止。基于遗传算法优化的BP神经网络算法流程如图5所示。

图5 基于遗传算法的BP神经网络算法流程图Fig.5 Flow chart of BP neural network based on genetic algorithm

3.2 预测模型的算法

3.2.1 遗传算法部分

首先将BP神经网络的初始权值、阈值作为遗传算法的初始群落进行初始化处理，然后进行复制、交叉、变异操作，并将种群中的新种群带到BP神经网络中进行迭代，寻找最佳权值和阈值。具体操作方式如下：

(1)初始化种群。将输入层与隐藏层、隐藏层与隐藏层、隐藏层与输出层之间的权值和阈值组成的实数串，作为遗传算法的初始化群落。

(2)适应度函数的确定。预测晶体直径和实际晶体直径之间的误差的绝对值作为个体适应度值F，则适应度的计算方式如下:

(4)

式中:F表示个体的适应度值;m表示BP神经网络的输出层节点数;di表示BP神经网络第i个节点的实际晶体直径;pi表示BP神经网络第i个节点的预测晶体直径。

(3)对优秀个体进行复制。采用各个个体被选中的概率与其适应度大小成正比的选择策略，即比例选择方法，其选择算子的计算方式如下:

(5)

式中:si表示选择算子;N表示种群中的个体总数;fi=k/Fi;Fi表示个体i的适应度值。

(4)交叉。种群中的两个个体按一定的概率进行随机交叉，在j点的两个个体pk和pl的交叉方式为：

(6)

式中:pkj和plj表示在j点两个个体;α是(1,0)之间的随机数。

(5)变异。随机将种群中的两个个体按照一定的概率进行变异，在j点个体pi的变异方式如下:

(7)

式中:pij表示在j点个体pi变异后所得到的个体;pmax为个体中的最大值;pmin为个体中的最小值;v为当前进化次数;vmax为最大进化次数;μ为介于(0,1)之间的随机数。

(6)判断新的个体是否满足最佳个体标准。若不能满足标准，则返回步骤(2)；若满足，则将最优个体分成BP神经网络的权值和阈值，重新调整网络参数，再次学习训练，直到达到学习的上限或所需精度为止。

3.2.2 BP神经网络部分

将遗传算法部分优化后的个体，解码获取权值、阈值，使用训练数据训练BP神经网络，然后使用遗传算法检验个体是否满足适应度标准，不满足标准的个体进行复制、交叉和变异等操作，随后重新进行网络训练，直到个体达到适应度标准或精度要求为止。具体操作方式如下:

(1)BP神经网络的初始化。X、Y分别为输入、输出层神经元的输入和输出向量，输入层节点数为n；输出层节点数为m。

(8)

式中，输入向量代表晶体直径与拉晶参数呈高度线性相关的特征值，输出向量代表晶体直径，二者都根据归一化公式(2)进行量化处理。

(2)计算第一层隐藏层输出。第一层隐藏层的节点个数为q，输入层和隐藏层之间的权值和阈值分别为ωij、λa，隐藏层的输出值为Ha，其计算公式如下：

(9)

式中:Haj为第一层隐藏层输出;f为激励函数。

(3)计算第二层隐藏层输出。第二层隐藏层的节点个数为q，第一层隐藏层和第二层隐藏层之间的权值和阈值分别为ωik、λb，第二层隐藏层的输出值为Hb，其计算方式如下：

(10)

式中:Hbk为第二层隐藏层输出。

(4)计算输出层输出。隐藏层和输出层之间的阈值和权值分别为ωil、λc，输出层的输出值为Hc，其计算方式如下：

(11)

式中:Hcl为输出层输出。

(5)计算误差并验证。预测输出Hc与实际输出Y之差的绝对值，即为误差e，其计算方式如下：

e=|Y-Hcl|

(12)

模型达到标准的误差最小值设为e0，如果min(e)

3.3 GA-BP神经网络训练

将BP神经网络所用训练集与测试集数据输入到GA-BP神经网络，进行训练与测试。图6为计算后所得结果图，由图6(a)可以看出该模型预测值与真实拉晶数据具有很高拟合性，由6(b)可以看出预测模型各点的平均相对误差较低，其平均相对百分比误差为0.029 42%。

图6 GA-BP神经网络晶体直径预测结果。(a)预测值与真实值的对比；(b)预测值与真实值的平均相对误差Fig.6 Crystal diameter prediction results of GA-BP neural network. (a) Comparison between predictive value and actual value; (b) average relative error between predictive value and actual value

BP神经网络预测模型与GA-BP神经网络预测模型的性能对比如表3所示，由表中可以看出GA-BP神经网络的最小相对误差、最大相对误差、平均绝对误差和平均相对误差均明显低于BP神经网络预测模型，而代表拟合优越度的绝对系数R2，GA-BP神经网络预测模型的绝对系数0.876 41优于BP神经网络预测模型的绝对系数0.470 27，因此GA-BP神经网络预测模型相对于BP神经网络预测模型在晶体直径预测方面具有更高的预测精度。

表3 两种神经网络预测模型性能对比Table 3 Performance comparison of two neural network prediction models

4 实验验证直径预测模型

本文所用训练数据与验证数据均来自同一台单晶炉的拉晶数据，此预测模型对其他同型号单晶炉预测精度如何，仍需要继续验证。因此，为了进一步验证预测模型的准确性和稳定性，随机选择8台CL120-97单晶炉做作为实验对象，将其完整拉晶数据分为八组，分别用所搭建的晶体直径预测模型进行仿真实验，图7为预测值与真实值的对比图，从图中可以看出，该模型对这8台单晶炉的预测性能，比用于训练神经网络的单晶炉的预测性能差，但仍有较高的拟合性。表4为这8台单晶炉预测值与真实值的平均相对百分比误差，平均值为0.095 71%，且其值均在0.05%～0.15%范围内，表明该晶体直径预测模型具有比较高的稳定性和准确性，能够用于晶体直径预测。

图7 预测值与真实值的对比图Fig.7 Comparison chart of predicted value and autual value

表4 预测值与真实值的平均相对百分比误差Table 4 Average relative percentage error between predicted value and actual value

5 结 论

本文针对传统的PID控制方法存在调节时间长、控制精度低以及基于大量假设的机理模型难以实际应用的问题，以现有CL120-97单晶炉拉晶车间的长期、海量晶体生长数据为基础，建立了一种基于BP神经网络的晶体直径预测模型，随后用遗传算法对预测模型进行优化，将实际拉晶数据对此模型进行训练，任选8台单晶炉验证模型，得出以下结论:

(1)所建立BP神经网络晶体直径预测模型对晶体直径预测的平均相对百分比误差为0.140 94%。

(2)预测模型使用遗传算法优化后，提高了对晶体直径的预测精度，对晶体直径预测的平均相对百分比误差为0.029 42%。

(3)预测模型对随机抽取的8台单晶炉进行直径预测,平均相对百分比误差为0.095 71%，且其值均在0.05%～0.15%范围内，表明该晶体直径预测模型具有比较高的稳定性和准确性，能够用于晶体直径预测。