具有半对称度量ρ-联络的共形平坦Yamabe孤立子的特征

潘 鹏, 刘建成

(西北师范大学 数学与统计学院, 兰州 730070)

1 引言及主要结果

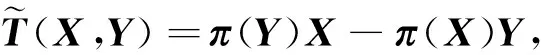
(1)

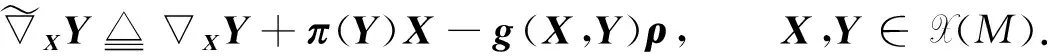
(2)

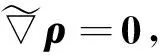
(3)

对Riemann流形(Mn,g)上的向量场V∈X(M), 如果存在光滑函数σ, 使得度量g沿V方向的Lie导数满足

LVg=2σg,

(4)

则称V为(Mn,g)上的一个共形向量场,σ为关于V的势能函数.当势能函数为常数0时, 称V为Killing型向量场[5].记(Mn,g)的数量曲率为r, 如果存在V∈X(M)及常数λ∈, 满足方程

LVg=(λ-r)g,

(5)

则称(Mn,g)为Yamabe孤立子, 记为(Mn,g,V,λ), 并称V为孤立子场,λ为孤立子常数[6].

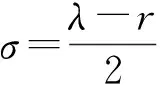
Yamabe孤立子是Yamabe流[6]

的自相似解, 其在共形几何中具有重要作用.由于Weyl张量是共形变换下的一个不变量, 且在三维情形中恒为0.因此, 具有某种结构三维Yamabe孤立子的几何(曲率)性质得到广泛关注. 例如： Sharma[7]研究了三维具有Sasakian结构的Yamabe孤立子; Wang[8]研究了三维具有Kenmotsu结构的Yamabe孤立子; Ghosh[9]将文献[8]的结果推广到一般维数的情形; Chaubey等[10]将半对称度量ρ-联络和Yamabe孤立子相结合, 研究三维具有半对称度量ρ-联络结构的Yamabe孤立子(M3,g,V,λ), 证明了M3的截面曲率为常数-1, 且孤立子常数λ=-6.

受文献[9]的启发, 本文将文献[10]的结论由共形平坦条件下推广到高维情形, 得到如下结果:

定理1设(Mn,g,V,λ)为n(n>3)维紧致的具有半对称度量ρ-联络的共形平坦Yamabe孤立子, 则其截面曲率为常数-1, 孤立子常数λ=-n(n-1), 且孤立子场V为Killing型向量场.

根据定理1, 并由常截面曲率的Riemann流形必为共形平坦的, 可得如下推论:

推论1设(Mn,g,V,λ)为n(n>3)维紧致的具有半对称度量ρ-联络的Yamabe孤立子, 则其具有常截面曲率的充要条件是(Mn,g,V,λ)是共形平坦的.

2 预备知识及引理

本文约定R,S,Q分别表示关于Levi-Civita联络的Riemann曲率张量、 Ricci曲率张量和Ricci变换,X,Y,Z,…表示(Mn,g)上任意光滑切向量场, Δ表示度量g的Laplace算子.根据式(2)和式(3), 一个具有半对称度量ρ-联络的Riemann流形(Mn,g)上成立如下等式：

Xρ=π(X)ρ-X.

(6)

由式(6), 通过计算有

R(X,Y)ρ=π(X)Y-π(Y)X,

(7)

从而

S(X,ρ)=-(n-1)π(X),

(8)

式(8)等价于

Qρ=-(n-1)ρ.

(9)

设V为n维Riemann流形(Mn,g)上的一个共形向量场, Yano[5]证明了

(LVS)(X,Y)=-(n-2)g(Xσ,Y)+Δσ·g(X,Y),

(10)

LVr=-2σr+2(n-1)Δσ.

(11)

此外, Riemann流形(Mn,g)(n≥3)上的Weyl张量C定义[11]为

引理1若(Mn,g)为n(n>3)维具有半对称度量ρ-联络的共形平坦Riemann流形, 则其数量曲率r满足ρ(r)=2(r+n(n-1)).

证明: 因为(Mn,g)是维数大于3的共形平坦Riemann流形, 故Weyl张量C=0, 从而由式(12)知

由Y,Z的任意性, 在式(13)中令Y=Z=ρ, 得

结合ρ是单位向量场, 即g(ρ,ρ)=1, 利用式(8),(9), 并对比式(7)计算可得

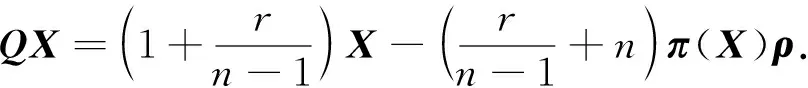
(15)

于是, 任取Y∈X(M), 由式(15)和式(6), 通过计算可得

取{ei}为局部单位正交标架场, 在式(16)中令X=Y=ei并对i求和, 结合恒等式

得

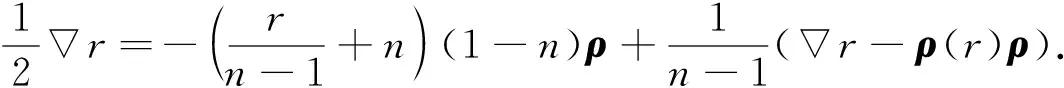
(17)

对式(17)两边与ρ做内积, 得ρ(r)=2[r+n(n-1)].证毕.

引理2若(Mn,g,V,λ)为n(n>3)维具有半对称度量ρ-联络的共形平坦Yamabe孤立子, 则数量曲率r是调和的.

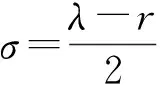
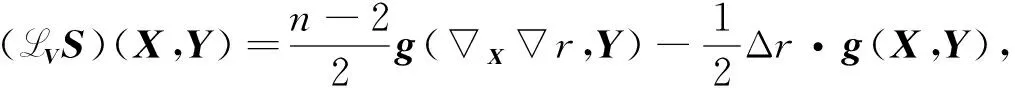
(18)

LVr=r(r-λ)-(n-1)Δr.

(19)

另一方面, 任取Y∈X(M), 对式(15)两边与Y做内积, 得

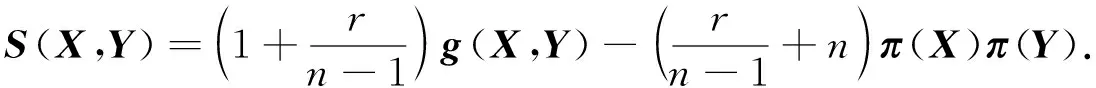
(20)

于是, 结合式(5),(18)～(20)及Lie导数算子的性质, 通过计算得

对比式(18),(21), 经计算有

取{ei}为局部单位正交标架场, 在式(22)中令X=Y=ei并对i求和, 利用式(5)及Lie导数算子的性质, 可得Δr=-Δr, 即Δr=0.证毕.

3 定理1的证明

下面证明定理1.因为g(ρ,ρ)=1=π(ρ), 故由式(5)得

(LVg)(ρ,ρ)=(λ-r)g(ρ,ρ)=λ-r.

(23)

又因为

(LVg)(ρ,ρ)=LVg(ρ,ρ)-2g(LVρ,ρ),

(24)

于是由式(23),(24)得

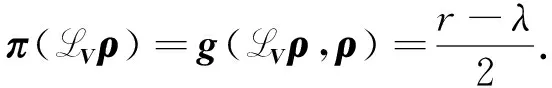
(25)

从而

(26)

另一方面, 在式(22)中, 令X=Y=ρ, 结合式(26), 经计算可得

又因为

ρ(ρ(r))=g(ρr,ρ)+g(r,ρρ)=g(ρr,ρ)+g(r,π(ρ)ρ-ρ)=g(ρr,ρ),

(28)

于是将式(28)代入式(27), 并结合引理1, 经计算得

Δr=2(n-1)[2n(n-2)+λ]+2(n-3)r.

(29)

根据引理2有

(30)

由于λ为常数, 故r是常数, 因此关于孤立子场V的势能函数σ也是常数.

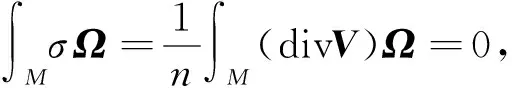
(31)

其中Ω表示体积元素.由于σ是常数, 因此由式(31)得σ=0.从而孤子场V是Killing型向量场.

此外, 由σ=0知λ=r, 代入式(30)得

λ=r=-n(n-1),

(32)

再结合式(15)得

QX=-(n-1)X.

(33)

最后将式(32),(33)代入式(13), 计算可得

R(X,Y)Z=-(g(Y,Z)X-g(X,Z)Y),

(34)

表明(Mn,g,V,λ)具有常截面曲率-1.证毕.