改进的基于层次距离的基因表达式编程特征选择分类算法

湛 航，何 朗*，黄樟灿，李华峰，张 蔷，谈 庆

（1.武汉理工大学理学院，武汉 430070；2.武汉大学数学与统计学院，武汉 430072）

（*通信作者电子邮箱helang@whut.edu.cn）

0 引言

特征选择（Feature Selection，FS）是数据挖掘中一项特别重要的数据预处理步骤，常用于去除数据中冗余和不相关的特征数据，降低计算复杂度，提升模型的效果［1-2］。特征选择在数字图像处理、文本分类、生物信息学、基因序列分析、金融时间序列分析以及医学数据分析等方面应用较为广泛［3-6］。常见的特征选择方法有：过滤式（filter）、嵌入式（embedding）和包裹式（wrpper）［7］。过滤式独立于学习器，在训练学习器之前完成特征的选择；嵌入式则将特征选择与学习器的训练结合，在一个优化过程中完成；包裹式则依据学习器的性能作为特征选择优劣的评价［7］。

特征选择是一个NP-hard 问题，对于具有n个特征的特征选择问题有2n个可能的特征子集［8］。在分类问题上，通过选取关键的特征，忽略不太重要的数据特征，构建出一个良好的分类器，进而提高分类预测效果［9］。选择的特征优劣对于构建出一个简洁、高效的分类系统有着重要的影响［10］。

国内外许多学者一直致力于研究这个问题。一些简单方法如穷举搜索算法、分支定界算法等［11］，这些方法可以挑选出最优的特征子集，但是这些方法的时间复杂度对于高维数据并不友好，在应用过程中也存在一些局限性。基于该问题，一些传统的机器学习方法被应用到这个方面，如决策树算法［12］给出了一种基于信息增益大小的特征选择分类方法；李占山等［7］提出了一种基于XGBoost 的特征选择算法；Moustakidis等［13］提出了一种基于支持向量机（Support Vector Machine，SVM）的模糊互补准则的特征选取方法。虽然机器学习方法拥有较快的求解速度，模型容易解释，但是它没有考虑特征与特征之间、特征与类别之间相关性。Sun 等［14］结合类别相关度，将最大相关性和最小冗余准则（max-Relevance and min-Redundancy，mRMR）扩展到了多标签学习，借助凸优化来优化特征初始分配的权重，从而获取特征排序；Sheikhi 等［15］将特征的冗余性替换为多样性，以量化候选特征相较于已选择子集的互补性，提出了正秩最大相关性及多样性的特征选择算法。尽管这些方法的原理较为简单，在小规模数据上拥有不错的表现，但对于大规模数据而言，在求解速度与求解精度上略显不足。

由于演化算法在NP-hard 问题上拥有着不错的表现，其计算复杂度相较于其他机器学习等方法更低，对于整个问题的解给出一种编码方案，而不是直接对问题的具体参数进行处理，它不用考虑问题本身的特殊知识背景，仅依靠种群个体内部的进化就能寻找到一个全局的较优解［7］，因而被大量用于特征选择问题上。Ghaemi 等［16］将求解连续变量优化问题的森林优化算法应用于离散的特征选择问题，有效地提高了分类器的分类精度；张翠军等［1］提出了一种平衡特征子集个数与分类精度策略的多目标骨架粒子群优化的特征选取算法；张梦林等［17］提出一种采用新的初始化策略和评估函数，以特征子集的准确率指导采样的基于离散域采样分类优化（Sampling-And-Classification optimization，SAC）特征选择算法，实验结果表明该方法可提高分类准确率，有好的泛化能力；李光华等［18］将随机森林的重要度评分作为蚁群的启发式信息，提出了一种融合蚁群算法和随机森林的特征选择算法；Tabakhi等［19］提出一种不依赖于其他学习算法，通过多次迭代寻优寻找最优子集的基于蚁群优化的无监督特征选择算法。

演化算法在特征选择领域的应用，使得人们不再关注数据领域内的具体知识，通过控制演化算法中种群的规模和搜索策略，采取合适的分类器，使得演化算法取得了不错的效果［11］。但是，上述演化算法往往还需要结合其他分类器才能在特征选择问题上使用，演化算法仅仅只是选择了特征，当前特征选择的优劣与否还需要借助分类器分类效果进行判断。并且，选择的特征与分类器仅仅只能反映出当前特征与该数据所属类别之间存在关系，无法直观说明关键特征与数据类别之间的一种可解释的映射关系。

基于该问题，Ma 等［20-21］提出了一种基于遗传规划（Genetic Programming，GP）算法的特征选择算法，利用GP 算法在函数发现上的优越性，构建出特征与类别之间的函数关系。实验结果表明，该算法提高了分类准确度，降低了特征选择率，还给出了显式函数关系式，揭示了特征与类别之间存在的关系。但是GP算法存在膨胀现象，种群个体在进化的过程中容易出现无用个体，影响种群进化效率，而基因表达式编程（Gene Expression Programming，GEP）算法相较于GP 算法拥有着更加高效的函数发现能力，能更好地克服GP 中的缺陷［22］。GEP算法在演化过程中过多的遗传算子参数设定使得算法结果容易受到干扰，而且决定演化方向的单一适应度值会使算法在解决复杂问题时容易陷入局部最优。崔未［23］提出了基于层次距离的基因表达式编程（GEP based on Layer Distance，LDGEP）算法，通过改变染色体结构，对个体的基因进行分层，定义种群个体层与层之间的距离，通过层次距离来选择遗传位点，使得个体有针对性地变异。实验结果表明，LDGEP 算法相较于传统GEP 算法有更好的发现函数的能力与速度，但在种群初始化及层次变异过程中存在一定的盲目性，影响种群进化速度。

基于此，本文提出了改进的基于层次距离的基因表达式编程特征选择分类算法（imporved Feature Selection and classification algorithm for LDGEP，FSLDGEP），通过改进种群的初始化方式，使得种群个体的随机初始化具有一定的导向性；同时，通过定义种群的层次邻域来改变种群个体的随机变异方式；并在原始的分类准确率评价指标上，考虑种群个体选择的特征数量，将其作为适应度评价指标之一，平衡维度缩减率与分类准确率之间的关系，构建出类别关于特征的函数，揭示出两者之间存在的函数映射关系。

1 基于层次距离的基因表达式编程算法

LDGEP 算法是由崔未基于GEP 算法改进而来的群智能演化算法。传统的GEP 算法中存在许多需要手动设定参数的遗传进化算子，如选择复制算子、转座算子、重组算子和变异算子等，而LDGEP 算法更改了原始GEP 算法的演化模式，重新定义了个体结构与个体相似性计算方法，将大量的进化算子减少至三个算子，且算子的参数无需设置，提升了算法求解问题的精度和速度。LDGEP 算法主要包括四步：种群初始化、适应度计算、选择操作和遗传操作。

1.1 种群初始化与个体编码解码

LDGEP 算法中初始种群个体的基因是随机生成的，基因由一个头部和尾部组成，其长度分别为h和t。头部符号从函数集和终止集中选取，尾部符号从终止集中选取。一般的函数集包含常用的数学运算符及一些初等函数，如{+，-，*，/，sin，exp，…}，终止集则通常由变量、常数等组成，如{x1，x2，1，2，e，…}。当基因头部与基因尾部长度满足约束式（1）时，个体初始化完成，重复多次，即可完成种群的初始化。

其中：t表示基因尾部长度；h表示基因头部长度；n表示函数集中符号的最大运算目数。

传统GEP 算法中的个体采用固定长度编码，只是在表达时部分基因不表达。为确保个体间的距离定义一致性以及表达式树结构的完整性，LDGEP 算法对未表达的节点采用TR（Null）节点补齐方法。LDGEP 算法中的个体编码长度由该个体的层数确定，其长度计算公式如式（2）：

其中：len表示个体长度；L表示层数。

如表达式a+sin(b)，该个体的编码及其表达式树结构如图1（a）。解码时，根据运算目数对未表达的基因采用TR 补齐，如图1（b），虚线代表补齐的TR 节点。再根据各节点运算符的性质以及二叉树的中序遍历方式，将个体的树结构转换成为数学表达式。

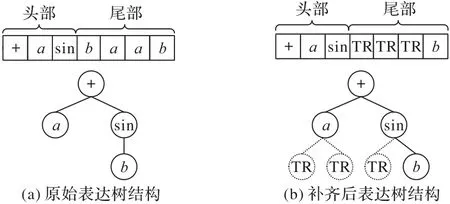
图1 表达树结构及补齐后表达树结构Fig.1 Structures of expression tree and complemented expression tree

1.2 距离定义

种群个体的层次示意图如图2 所示，每层个体的数量为2l-1，其中l表示当前的层数。

图2 个体层次示意图Fig.2 Schematic diagram of individual layer

LDGEP 算法对每个个体的每一层给定一个权值，用以区分不同层对于个体的影响。种群个体的层次距离为基于加权的汉明距离，计算公式所示：

其中：dij(l)表示第i个个体与第j个个体在第l层的层次距离；L表示个体的总层数；Dij(l)为第i个个体与第个j个个体在第l层的汉明距离。wl表示第l层的权重，其计算公式如下所示：

其中：l表示层数。随着层次的递增，层次重要性越低，从而对解码后的个体的表达影响越低。

1.3 遗传操作

1.3.1 遗传位点选择

由于每一层对于种群个体的表达有不同的影响，通过对层次距离不同的层采用遗传操作，使种群个体向更优秀的个体靠近。通过计算每一层个体间的层次距离确定遗传位点。遗传位点的确定规则如下所示：

其中：dij(l)表示第i个个体与第j个个体在第l层的层次距离；layerij表示第i个个体与第j个个体遗传位点层。若该层层次距离小于0.5，则忽略该层，转入下一层。否则，用layerij记录下当前所处层，并对其执行三种遗传操作：1）对两个个体的第l+1 层及之后剩余层进行基因重组；2）对两个个体的第l层进行层间重组；3）对该个体的第l+1 层及之后剩余层进行层次变异。

1.3.2 基因重组

根据式（5），确定遗传选择层，其操作机制如图3 所示，两个个体第一层的层次距离大于0.5，确定遗传位点为第二层，基因重组算子对两个个体剩余部分执行重组。

图3 基因重组Fig.3 Gene recombination

1.3.3 层间重组

根据式（5），确定遗传选择层，层间算子对该层执行层间重组。其操作机制如图4，两个体的第一层层次距离为0，第二层层次距离等于0.5，对两个个体的第二层进行重组。

图4 层间重组Fig.4 Recombination between layers

1.3.4 层次变异

为避免无用个体的产生，执行层次变异时，第一层符号从函数集选择，最后一层符号从终止集选择，而其他层则从函数集与终止集中选择。根据式（5），确定遗传选择层，其操作机制如图5 所示，第一层距离大于0.5，层次变异算子从第二层开始执行变异，于是该个体随机从函数集和终止集中选择了一个符号，使得第二层的一个基因由双目运算符变成单目运算符，同时为保证个体正确表达，对其子节点进行TR补齐。

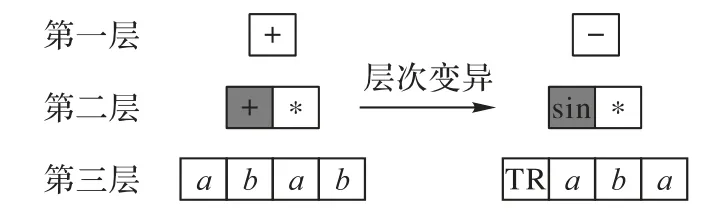
图5 层次变异Fig.5 Layer mutation

2 改进的LDGEP特征选择分类算法

由于LDGEP 算法的种群个体有着特殊的基因编码、解码方式，因此，当个体的头部基因有较多终止符时，容易产生一些无用个体。同时，种群个体随机地从函数集和终止集中选择符号来执行层次变异操作，这种随机性减缓了种群的进化速度。针对上述LDGEP 算法的不足，本文提出了一种依概率种群初始化方式和基于邻域的层次变异策略，同时，为减少特征的选择数量，将个体选择的特征维度缩减率作为判断最优个体的指标之一。该算法流程如图6所示。

图6 FSLDGEP流程Fig.6 Flowchart of FSLDGEP algorithm

2.1 依概率种群个体初始化

在LDGEP 算法中，每层符号的选择随着层次的不同而不同。但是，个体编码中过多的终止集符号使得个体的表达提前结束，容易产生无用的表达式。本文提出了依概率种群个体初始化方法，通过概率约束，使个体基因头部更侧重于选择函数符号，增加产生有效表达式个体的数量，提高种群的进化速度。选择概率的计算方式如式（6）：

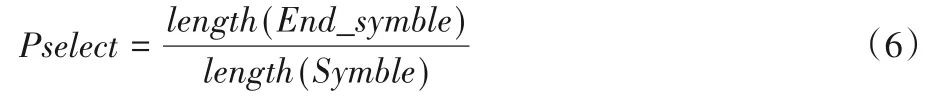
其中：Pselect表示选择概率；End_symble表示终止集；Symble表示函数集和终止集的合集；length(·)表示取集合的长度。

依概率种群个体初始化方法如下所示：

2.2 基于邻域的层次变异

LDGEP 算法针对不同层产生的层次变异，其变异选择符号集不同。而变异的随机性使得种群个体在进化过程中容易产生低质量的解，影响算法的寻优速度。本文提出了层次邻域的概念，层次邻域是由种群中优秀个体的各层次符号组成，当种群个体发生层次变异时，个体基因从当前层次邻域中选取变异符号，使变异个体的基因向着优秀个体基因的方向靠近，提升算法的寻优能力。层次邻域定义如下。

设种群中的个体数为N，层数为L，计算个体的适应度值，并从大到小排列，取前N/2 个个体作为优秀个体，设前N/2 个个体及其基因编码为：

将个体x1，x2，...，xN/2中每一层的符号提取去重后构成的集合作为该层的一个层次邻域，因此可以得到L个层次邻域式（8）：

其中：m1、m2、…、mk分别表示去重后每一层的符号总个数，即该层次邻域的大小。种群个体从每一层的层次邻域中选择符号进行层次变异。基于层次邻域的变异策略如下所示：

2.3 改进的适应度值计算

LDGEP 算法仅将分类准确率CA（Classification Accuracy）作为判断当前个体是否最优的指标，而忽视特征维度缩减问题，导致算法得到的函数表达式变得复杂的同时也让表达式对特征数据较为依赖和敏感。为了提高算法对于数据特征选择的性能，本文引入特征的维度缩减率DR（Dimension Reduction）作为新的适应度评价指标之一，将其与CA加权求和后的值作为优化目标，改变种群单一优化目标的局限性，平衡了分类函数分类准确率和维度缩减率。适应度值计算方式如下：

其中：fitness表示个体的适应度值；λ1表示准确率的权重；λ2表示维度缩减率的权重。为保证分类准确率在适应度值中的主导地位，避免维度缩减率的影响，λ1与λ2满足λ1≫λ2>0。

CA描述的是分类器分类效果的好坏，计算公式如下：

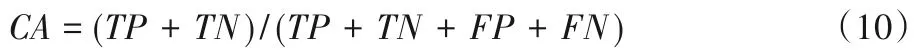
其中：TP（True Positives）表示被模型分类为正的正样本数；TN（True Negatives）表示被模型分类为负的负样本数；FP（False Positives）表示被模型分类为负的正样本数；FN（False Negatives）表示被模型分类为正的负样本数。

特征选择数量与DR之间满足关系式（11）：

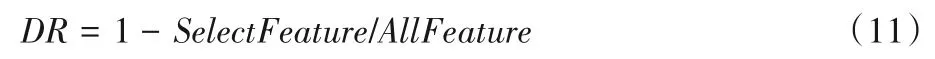
其中：SelectFeature表示个体选择的特征个数；AllFeature表示数据集的总特征数。故DR可替代特征选择数量来描述算法在特征选择上的优劣。

CA描述的是通过选择的特征构造的分类函数对数据分类正确的概率；DR描述的是维度缩减率，即未选择的特征在总体特征中的占比。特征选择的数量越小越好，而CA越大越好，两者共同用来描述算法性能优劣时评价不统一，又DR由选择特征的数量决定，且DR的大小变化与描述算法性能优劣一致，故采用DR替代特征选择数量来侧面描述算法在特征选择上的优劣。CA与DR共同构成本文算法适应度值计算的相关指标。

2.4 算法步骤

第1 步 初始化参数。确定种群大小NIND，种群迭代次数MAXGEN，终止集END_SYMBLE，函数集FUNC_SYMBLE，个体编码层数L。

第2 步 依概率种群初始化。根据式（6）计算选择概率，根据依概率种群初始化算子从FUNC_SYMBLE和END_SYMBLE中选择2L个符号作为个体X，构造初始种群。

第3 步 种群适应度计算。将种群个体的编码转换成对应的分类函数，通过计算函数中特征数据变量的个数以及利用分类函数对数据进行分类，得到维度缩减率及分类准确率，再根据式（9）计算每个个体的适应度值。

第4 步 个体更新。对个体执行精英策略轮盘选择复制算子、基因重组、层间重组算子以及基于邻域的层次变异等遗传操作，得到更新后的个体NewX。

第5 步 终止条件判断。如果gen>MAXGEN，则终止，得到分类函数、维度缩减率以及分类准确率；否则令gen=gen+1，X=NewX，返回第3步。

2.5 时间复杂度分析

设最大迭代次数为MAXGEN，种群规模为NIND，种群个体编码长度为l，数据样本量M，由2.4 节算法步骤可知，在一个完整的循环过程中：第1步与第5步的时间复杂度可以忽略不计；第2 步中由于需要遍历个体X，针对长度为l的个体X，初始化过程的时间复杂度近似为O(NIND⋅l)；第3 步操作由于每个个体均需要计算一次样本数据的结果，其时间复杂度近似为O(NIND⋅M)；第4步中均是个体自身以及个体与个体之间的遗传操作，其最差情况下的时间复杂度为O(NIND⋅l)。因此本文算法的总体时间复杂度近似可表示为O(MAXGEN⋅NIND⋅(M+l) +NIND⋅l)。

3 仿真实验

3.1 实验数据

实验采用UCI［24］机器学习库中的7 个分类数据集Hepatitis、Ionosphere、Musk1、Sonar、Heart-Statlog、WDBC（Wisconsin Diagnostic Breast Cancer）和WPBC（Wisconsin Prognostic Breast Cancer）。其中Hepatitis 数据中存在多个数据缺失的情况，本文利用其同类特征数据的平均值替代。为避免不同特征数据的量纲影响，本文对7 组数据分别进行了归一化处理，归一化方法如式（12）所示：

其中：表示归一化后特征数据值；Fvalue表示未归一化特征数据值；Fmin表示未归一化特征数据中的最小值；Fmax表示未归一化特征数据中的最大值。

数据集详细信息如表1 描述。实验仿真在Intel Core i5-4460 3.20 GHz CPU，4.0 GB 内存，64 位Windows 7 操作系统的PC上实现，软件环境为Matlab R2017b。

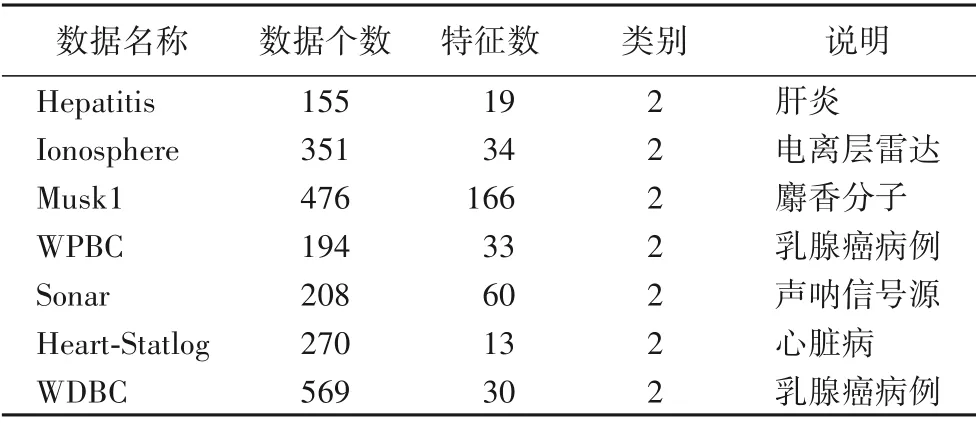
表1 实验数据集说明Tab.1 Description of experimental datasets

3.2 实验参数

FSLDGEP 参数设置为：种群大小40，种群迭代次数300，个体层数的值如表2，常数个数10 以及函数集{+，-，*，/，sqrt，exp，sin，cos，tan，lg}，终止集由各类特征数据和常数组成。经过多组数据实验结果比较，将式（9）中λ1的权重值设定为1，λ2权重值设定为0.01。

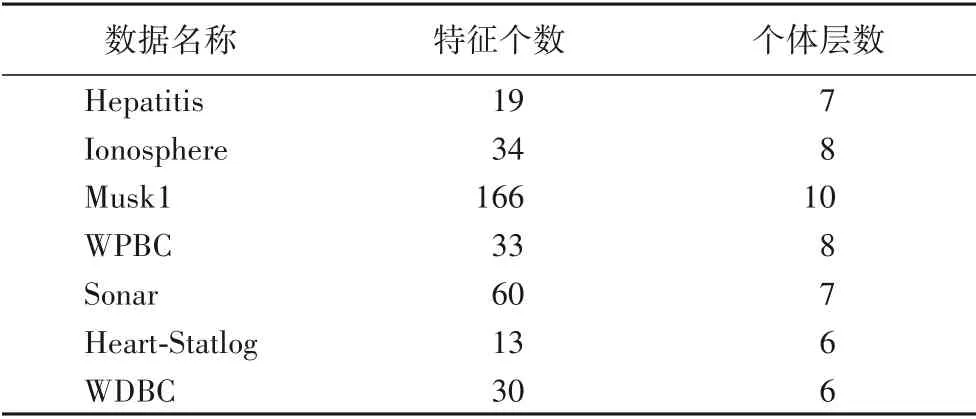
表2 实验数据集参数Tab.2 Parameters of experimental datasets

为了防止产生过拟合的问题，本文采用2 折交叉、5 折交叉、10 折交叉与70%-30%这4 种验证方式。其中，k折交叉验证方式（k表示2、5、10）表示：将数据集分成k份，训练时每次取k-1 份数据做训练，剩余1 份数据做测试，使得每一份数据都能基于k-1 份数据训练得到的结果做测试，验证算法性能。70%-30%验证方式表示取原始数据集中的70%的数据作为训练集，训练算法；30%的数据作为测试集，验证算法性能。

对于分类问题，本文采用IF-THEN规则［23］，根据算法输出结果与阈值比较，判断出当前数据特征所属类别，IF-THEN 规则如下：

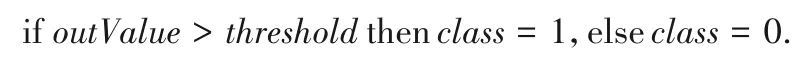
其中：outValue表示输出结果；threshold表示阈值，在本文中，阈值的大小设定为0；class表示数据类别。

评价算法的性能主要使用两个指标［17］：DR和CA。CA越大，算法得到的映射函数的分类性能越好；DR越大，则算法选择特征数量越少，维度缩减能力越强，特征选择能力越强。

3.3 实验结果

为验证本文算法对于构建特征及其类别之间函数映射关系的可行性，本文对不同数据在不同的验证方式下独立重复了10 次实验，取10 次实验中测试集的最优分类准确率TBCA（Testset Best CA）和最优分类准确率对应的维度缩减率TBDR（Testset Best DR）及其相对应的分类函数TBF（Testset Best Function），其结果展示如表3所示。

表3的最优分类函数TBF及式（13）中的Fi分别表示数据中的第i(i=1，2，…，M，M表示数据的维度)个特征数据，该特征数据与原始数据集中的特征数据一一对应。c7表示常数。将对应的特征数据带入表5 中的最佳分类函数中进行计算，即可判断出当前特征数据所属类别。

表3 最优分类准确率及维度缩减率对应函数Tab.3 Functions corresponding to optimal classification accuracy and dimension reduction rate

式（13）表示Musk1 数据集在10-fold 交叉验证方式下，10次独立重复实验中，最优分类准确率对应的数据特征及其对应类别之间的映射函数。

从表3 可看出：FSLDGEP 在92%的测试上TBCA超过80%，在57%的测试上TBCA超过90%。在71%的测试上TBDR超过85%。在10-fold 验证情况下，FSLDGEP 针对Hepatitis、Ionosphere以及WDBC数据集，分别选择了3个、5个以及4 个特征，构建出的分类器函数最优分类准确率达到100%，针对含有60 个特征的Sonar 数据集，FSLDGEP 仅保留了3 个特征，构建出了最佳分类准确度95.24%的分类函数；针对含有166 个特征的Musk1 数据集，FSLDGEP 也仅仅是选择了使用22 个特征去构造映射函数。对于大部分特征选择算法而言，它们仅仅反映了一种特征及其类别之间一种不明确的关系。但FSLDGEP 可以从原始特征中选择少量的特征构造出与数据类别相关的有效映射函数关系式，其形式较为简单，仅通过几个初等函数组合得到，能更好地解释特征与类别之间的关系，虽然式（13）相对其他分类函数更为复杂，但由于Musk1数据拥有较多的特征，其类别由较多的特征决定，无法通过少数特征与线性或非线性函数构造得到分类函数，本文算法在保证维度缩减率及分类准确率较好的条件下，从而得到了一个较为复杂的分类函数。尽管本文算法在其他数据集上有较好的表现，但对于Musk1 数据集仍存在一点不足。通过最佳分类准确率及维度缩减率可以发现，最佳分类准确率与维度缩减率之间相差不大，大部分相差在10%左右，说明本文算法能够有效地平衡特征选择数量以及分类准确率之间的关系，在提高分类正确率的同时也能减少一定的特征选择的数量。

为验证本文算法构建的映射函数在数据分类上的有效性及优越性，将FSLDGEP 和公开发表文献中的算法在相同的数据集和验证方式下的实验结果进行比较，每一次验证均重复10 次，取其平均值。对比结果中：加粗数值表示在不同验证方式下的最优值；“—”表示该算法不存在该结果或无需采用该类方法策略。

各对比算法采用的分类器有J48、3 近邻（3-Nearest Neighbor，3NN）分类算法、1 近邻（1-Nearest Neighbor，1NN）分类算法、5近邻（5-Nearest Neighbor，5NN）分类算法、基于径向基核函数的支持向量机（SVM based on Radial basis kernel function，Rbf-SVM）、SVM、随机森林算法（Random Forests，RF）、决策树（Decision Tree，DT）等方法。

表4 为FSLDGEP 与森林优化特征选择算法（Feature Selection based on Forest Optimization Algorithm，FSFOA）［16］、基于邻域有效信息比的特征选择（Feature Selection based on the Neighborhood Effective Information Ratio，FS-NEIR）算法［25］、邻域软边界特征选择（feature evaluation and selection based on Neighborhood Soft Margin，NSM）［26］算法、基于离散互信息的分步优化特征选择算法（Step by step Optimization Feature Selection algorithm based on Discrete mutual information，SOFS-D）［5］、基于邻域互信息的分步优化特征选择算法（Step by step Optimization Feature Selection algorithm based on Neighborhood mutual information，SOFS-N）［5］、基于蚁群优化的无监督特征选择算法（Unsupervised Feature Selection algorithm based on Ant Colony Optimization，UFSACO）［19］等算法在Hepatitis数据集上的实验结果。

表4 Hepatitis数据集上的实验结果比较Tab.4 Comparison of experimental results on Hepatatis dataset

表5 为FSLDGEP 与FSFOA、新的森林优化算法的特征选择算法（New Feature Selection based on Forest Optimization Algorithm，NFSFOA）［2］、NSM、FS-NEIR、UFSACO、基于模糊互补准则的支持向量机特征选择方法（novel SVM-based feature selection method using a Fuzzy Complementary criterion，SVMFuzCoc）［13］、基于离散域采样分类优化特征选择算法（Feature Selection algorithm using Sampling-And-Classification optimization algorithm，FSSAC）［17］、基于粒子群优化的特征选择方法分类的新初始化和更新机制（本文记为PSO（4-2），4-2表示原文作者采用自定义的第4 种策略做种群初始化，自定义的第2种策略更新种群）［27］、基于互信息的包裹式特征选择混合遗传算法（Hybrid Genetic Algorithm for Feature Selection wrapper based on mutual information，HGAFS）［28］等算法在Ionosphere数据集上的实验结果。

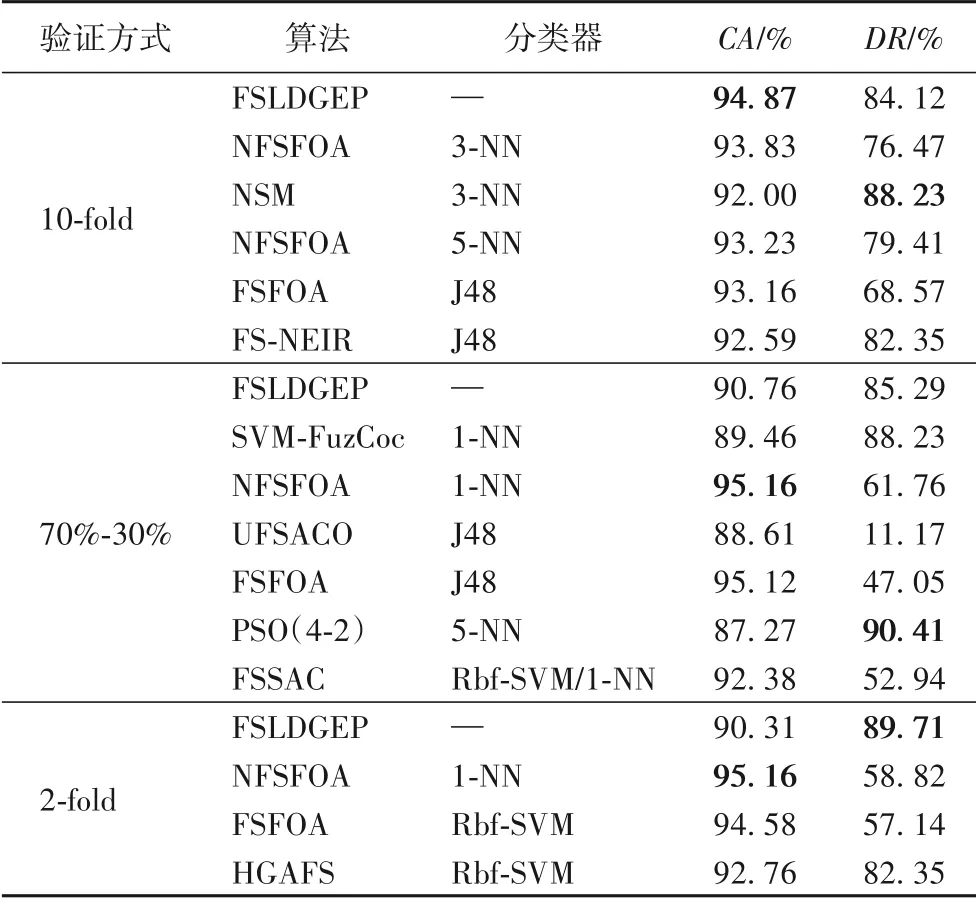
表5 Ionosphere数据集上的实验结果比较Tab.5 Comparison of experimental results on Ionosphere dataset

表6 为FSLDGEP 与联合互信息特征选择算法（Joint Mutual Information feature selection algorithm，JMI）［29］、基于动态变化类的特征选择算法（Dynamic Change of Selected Feature algorithm with the class，DCSF）［29］、最小化冗余信息的动态特征选择方法（Dynamic Feature Selection method with Minimize Redundancy Information，MRIDFS）［29］、最小冗余与最大相关的特征选择算法（Minimal-Redundancy-Maximal-Relevance feature selection，MRMR）［30］、最大相关性和最大独立性特征选择算法（Max-Relevance and max-Independence feature selection algorithm，MRI）［30］等在Musk1 数据集上的实验结果。

表6 Musk1数据集上基于10-fold验证方式的实验结果比较Tab.6 Comparison of experimental results based on 10-fold verification on Musk1 dataset

表7 为FSLDGEP 与基于特征子集区分度的顺序前向搜索特征选择算法（feature selection algorithm of Discernibility of Feature Subset based on Sequential Forward Search，DFSSFS）［10］、基于特征相关性的顺序前向搜索特征选择算法（feature selection algorithm of Correlation of Feature Selector based on Sequential Forward Search，CFS-SFS）［10］、基于皮尔逊相关系数绝对值的顺序前向搜索相关特征选择（Correlation based Feature Selector based on the absolute of Pearson’s correlation coefficient on Sequential Forward Search，CFSPabs-SFS）［10］、基于特征子集区分度的顺序后向搜索特征选择算法（feature selection algorithm of Discernibility of Feature Subset based on Sequential Backward Search，DFS-SBS）［10］、基于特征相关性的顺序后向搜索特征选择算法（feature selection algorithm of Correlation of Feature Selector based on Sequential Backward Search，CFS-SBS）［10］、基于皮尔逊相关系数绝对值的顺序后向搜索相关特征选择（Correlation based Feature Selector based on the absolute of Pearson’s correlation coefficient on Sequential Backward Search，CFSPabs-SBS）［10］等算法在WPBC数据集上的实验结果。

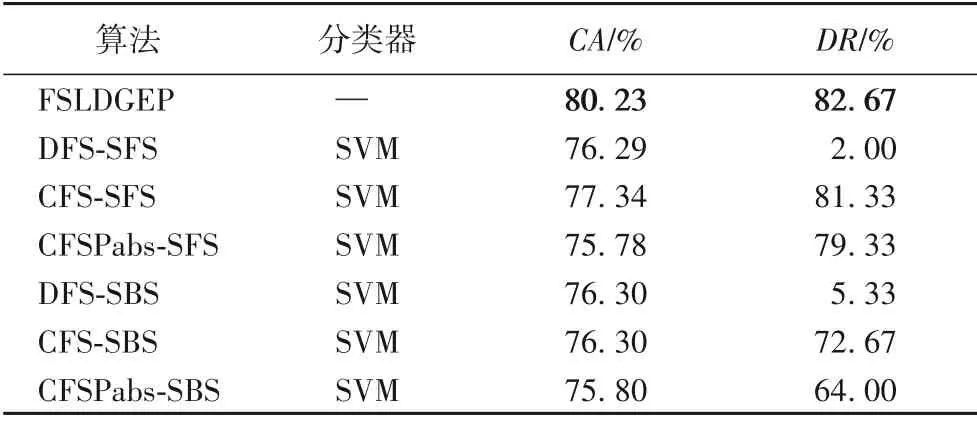
表7 WPBC数据集上基于5-fold验证方式的实验结果比较Tab.7 Comparison of experimental results based on 5-fold verification on WPBC dataset

表8 为FSLDGEP 与FSFOA、FS-NEIR、基于高斯核粗糙集依赖性的特征选择算法（Feature Selection algorithm based on Dependency of Gaussian kernel rough set，FS-GD）［31］、基于邻域粗糙集依赖性的特征选择算法（Feature Selection algorithm based on Dependency of Neighborhood rough set，FS-ND）［32］、基于邻域识别率的特征选择算法（Feature Selection algorithm based on Neighborhood Recognition Rate，FS-NRR）［33］、NFSFOA、粒子群优化（Particle Swarm Optimization，PSO）算法［27］、SVM-FuzCoc、改进的基于乌鸦搜索算法的特征选择算法（Improved Feature Selection algorithm based on Crow Search Algorithm，IFSCrSA）［34］等在Sonar数据集上的实验结果。

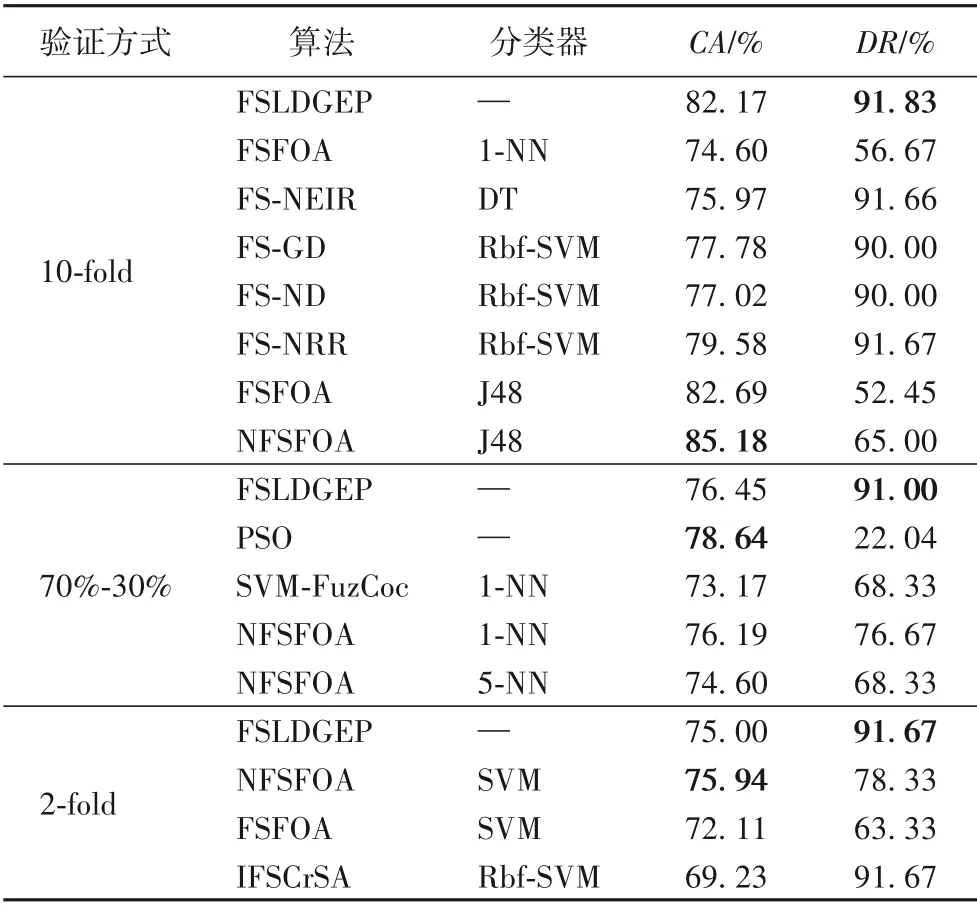
表8 Sonar数据集上的实验结果比较Tab.8 Comparison of experimental results on Sonar dataset

如表9 为FSLDGEP 与FSFOA、NSM、NFSFOA、FS-NEIR、UFSACO、IFSCrSA、融合Shapley 值和粒子群优化算法的混合特征选择算法（Shapley Value and Particle Swarm Optimization，SVPSO）［35］、新的Shapely 值嵌入遗传算法（novel Shapely Value Embedded Genetic Algorithm，SVEGA）［36］等在Heart-Statlog 数据集上的实验结果。

表9 Heart-Statlog数据集上的实验结果比较Tab.9 Comparison of experimental results on Heart-Statlog dataset

如表10 为FSLDGEP 与SOFS-D、SOFS-N、DFA-SFS、CFSSFS、CFSPaBS-SFS、DFS-SBS、CFS-SBS、CFSPaBS-SBS、UFSACO、相关性冗余特征选择（Relevance-Redundancy Feature Selection，RRFS）算法［19］、融合蚁群算法和随机森林的特征选择方法（feature selection method based on Ant Colony Optimization and Random Forest，ACORF）［18］等在WDBC 数据集上的实验结果。

表10 WDBC数据集上的实验结果比较Tab.10 Comparison of experimental results on WDBC dataset

从表4～10 中分类准确率的实验结果可以看出，关于Hepatitis、Ionosphere、Musk1、WPBC、Heart-Statlog 和WDBC 数据集在10-fold条件验证下以及关于WPBC和WDBC数据集在5-fold 条件验证下，本文算法均达到最好；但FSLDGEP 在Ionospherre、Sonar 和Heart-Statlog 这三个数据集中，存在部分交叉验证的情况下，其分类准确率分别低于NFSFOA、PSO 算法和IFSCrSA 算法。虽然FSLDGEP 不能保证在每一种验证条件下的分类准确率最高，但是FSLDGEP 的分类准确率与数据集的当前最优分类准确率之间相差不大，并且在10-fold 验证条件下，FSLDGEP 在大部分数据集上能够取得最好的分类准确率。

从表4～10 中维度缩减率的实验结果可以看出，关于Hepatitis、WPBC、Sonar 和WDBC 数据集在几种不同验证条件下，本文算法均达到最优。但在Ionosphere 数据集上基于10-fold 与70%-30% 验证条件下分别低于NSM 算法与PSO（4-2）算法；在Heart-Statlog 数据集上基于10-fold 与2-fold验证条件下分别低于NSM算法与NFSFOA算法。尽管维度缩减率相较于上述算法略有不足，但FSLDGEP 在大部分数据集上的不同验证方法下的维度缩减率超过了80%，只有Hepatitis 和Heart-Statlog 数据集基于10-fold 验证条件下的维度缩减率分别为77.89%和65.38%。出现这样的情况并不能说明本文算法在10-fold 验证条件下不适用于Hepatitis 和Heart-Statlog 数据集；相反地，利用本文算法对这两个数据集进行特征选择分类后，均能达到该数据集在10-fold 验证条件下的最高分类准确率。

综合表4～10 中的CA与DR的实验结果可以发现，FSLDGEP 在Musk1、WPBC、WDBC 这3 个数据集上均取得了最好结果。尽管在有些数据集的不同验证条件下，FSLDGEP不能使得CA与DR同时取得最优值，但是，FSLDGEP 在大部分情况下能够使得CA与DR形成一种互补的情况。在Ionosphere 数据集上，基于10-fold 验证条件下，FSLDGEP 与NSM 算法相比，在DR上低4.11 个百分点，但CA上高2.87 个百分点；基于70%-30%与2-fold 验证条件下，FSLDGEP 与NFSFOA 算法相比，在CA上分别低4.4 与4.85 个百分点，但在DR上高23.53与30.89个百分点。在Sonar数据集上，基于10-fold与2-fold验证条件下，FSLDGEP 与NFSFOA 相比，在CA上低3.01与0.94个百分点，但在DR上高26.83与13.34个百分点；基于70%-30%验证条件下，FSLDGEP 与PSO算法相比，在CA上低2.19 个百分点，但DR上高68.96 个百分点；从CA与DR的结果也可以反映出，FSLDGEP 相较于其他算法来说占有一定的优势。

综合表3～10 的结果可以看出，无论是低维度特征数据Heart-Statlog，还是高纬度特征数据Musk1，FSLDGEP 都能够很好地发现数据特征及其所属类别之间的一个函数映射关系，且发现的函数能很好地平衡CA与DR。说明了本文算法生成的映射函数在数据特征提取分类上的可行性与有效性，同时说明了本文算法在数据特征选择分类上的优越性。

4 结语

本文针对特征选择算法无法揭示特征与其类别之间存在的具体关系的问题，提出了一种改进的层次距离基因表达式编程特征选择分类算法。该方法首先依概率对种群个体进行初始化，使个体头部侧重于函数符号的选择，减少无效基因的表达，提高了种群进化的速度；其次，通过层次距离确定遗传位点，并对其进行遗传操作，利用定义的层次邻域，使得种群个体的层次变异具有导向性，提升了算法寻优的精度；最后，引入新的适应度评价指标，综合考量了分类准确率和维度缩减率，改变了种群更新机制的局限性，使得算法能够更有效地建立特征与类别之间的函数关系，为特征的选择提供了一种新的思路。在7 个数据集上进行仿真实验，与SVM、NN 等分类器相比，FSLDGEP 在能够有效构建特征及其类别之间函数关系式，减少特征选取的数量，提升分类效果。针对高维特征数据，如何保证高分类率和低特征选择率的同时，仍能得到一个较为简单的函数表达式，将是进一步的研究工作。