2021年高考“平面向量”专题解题分析
李波 段喜玲 张晓斌


摘 要:对2021年高考数学试卷中的平面向量试题,按照不同知识点进行归纳整理,结合《普通高中数学课程标准(2017年版2020年修订)》,从新高考的角度进行解题分析,侧重于向量问题在代数与几何两个维度的解法探究,重点体现向量“数”与“形”的双重属性,形成解决向量问题的常用思想方法.
关键词:2021年高考;平面向量;试题解析
《普通高中数学课程标准(2017年版2020年修订)》(以下简称《标准》)指出,向量理论具有深刻的数学内涵、丰富的物理背景. 向量既是代数的研究对象,也是几何的研究对象,是沟通代数与几何的桥梁. 向量是描述直线、曲线、平面、曲面及高维空间数学问题的基本工具,是进一步学习和研究其他数学领域问题的基础,在解决实际问题中发挥着重要作用.
新高考要求学生理解向量的基本概念、基本运算及物理背景,综合运用代数方法和几何方法,通过“数”的运算处理“形”的问题,通过“形”的变化解释“数”的运算结果,促进学生在解决一些数学有关的实际问题中发展数学学科核心素养,提升数学运算能力、综合分析能力和理性思维能力.
一、试题分析
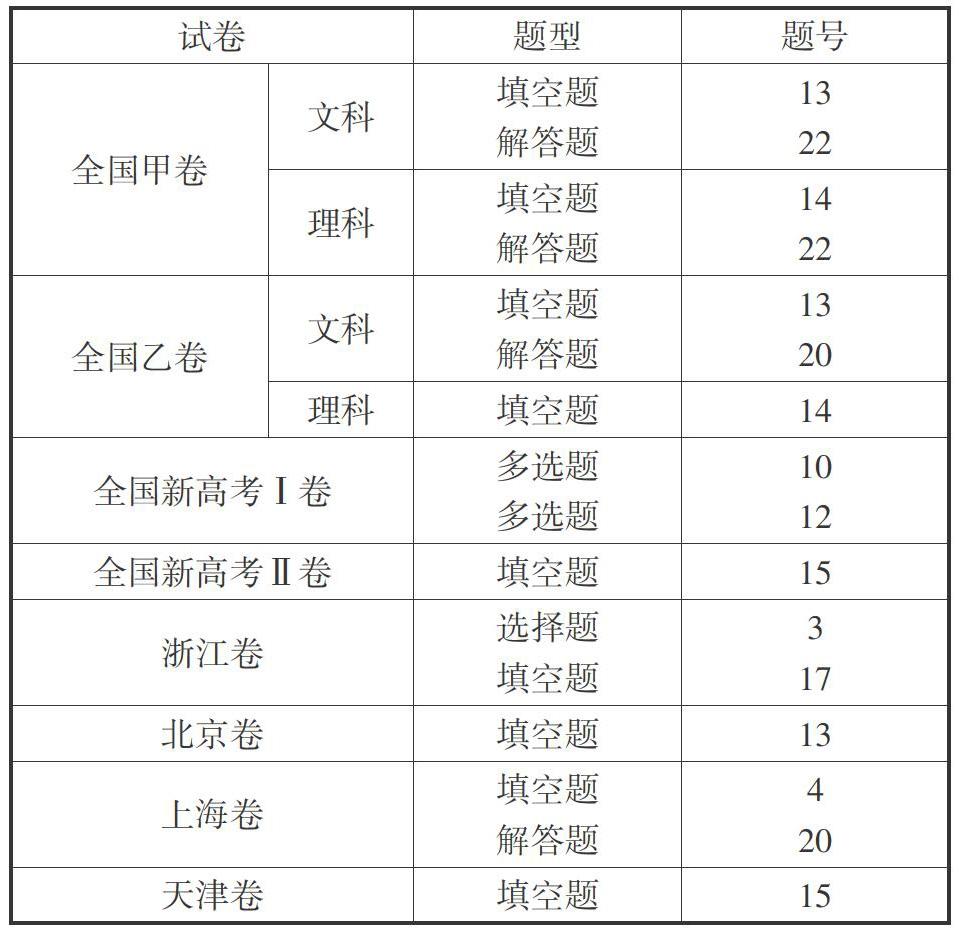
综观2021年高考数学平面向量试题,题型结构与分布情况如下表所示.
[试卷 题型 题号 全国甲卷 文科 填空题
解答题 13
22 理科 填空题
解答题 14
22 全国乙卷 文科 填空题
解答题 13
20 理科 填空题 14 全国新高考Ⅰ卷 多选题
多选题 10
12 全国新高考Ⅱ卷 填空题 15 浙江卷 选择题
填空题 3
17 北京卷 填空题 13 上海卷 填空题
解答题 4
20 天津卷 填空题 15 ]
从试卷结构来看,2021年高考数学平面向量试题仍以选择题和填空题为主,部分试卷有解答题(解析几何与向量结合、坐标系与参数方程与向量结合). 对平面向量内容的考查整体呈现平稳有序、题量适中、难度适当的特点. 主要考查平面向量的基本概念、线性运算、平面向量基本定理、坐标运算、平面向量的平行与垂直的充要条件、数量积及其应用等核心知识. 特别是从数形结合的角度考查向量的代数特性和几何特性,通过建立坐标系,实现代数方法(坐标运算)与几何直观(向量运算)的完美融合.
平面向量题型的解法呈现如下特点:平面向量模的问题,通过代数法(向量运算)或几何法(向量投影)解决,如全国甲卷文科第13题;平面向量的平行与垂直问题,通过平行与垂直的充要条件转化为向量的坐标求解,如全国甲卷理科第14题、全国乙卷文科第13题、全国乙卷理科第14题;数量积及其应用问题,通过代数法(向量的坐标运算、线性运算)、平面几何构造法解决,如全国新高考Ⅰ卷第10题、全国新高考Ⅱ卷第15题、浙江卷第3题、北京卷第13题、上海卷第4题;立体几何题转化为平面向量问题求解,如全国新高考Ⅰ卷第12题;平面向量问题转化为立体几何解决,如浙江卷第17题;等等.
高考平面向量试题总体上按照“方向是核心,平稳是关键”的原则,深化基础性、优化情境设计,聚焦核心素养,突出对关键能力的考查,增强试题的开放性、灵活性. 试题突出数学本质,重视理性思维,坚持素养导向、能力为重的命题原则,体现了基础性、综合性、应用性和创新性的考查要求. 充分发挥高考的育人功能和导向作用,促進了素质教育的发展.
二、试题分类解析
1. 平面向量模的运算
例1 (全国甲卷·文13)若向量[a,b]满足[a=3],[a-b=5],[a · b=1],则[b]的值为 .
分析:该题主要考查平面向量的模、向量的减法运算. 可以通过向量模[a-b2]的展开式,结合[a · b=1]求解[b]. 同时,也可以由向量减法的三角形法则,通过向量投影,充分利用向量的几何属性,利用余弦定理建立等量关系求解.
解法1:因为[a-b=5],
所以[a-b2=a2+b2-2a · b=9+b2-2=25].
所以[b=32].
故答案为[32].
解法2:如图1,记[a=OA],[b=OB],[θ=a,b],则[a-b=BA].
[C][B][A][O] [图1]
由[a=3],[a-b=5],知[⇒OA=3],[BA=5].
由[a · b=1],得[⇒abcosθ=1].
所以[bcosθ=1a=13],即[b]在[a]方向上的投影的长为[bcosθ=OC=13].
在[Rt△BOC]中,[cosθ=OCb=13b].
在[△BOA]中,由余弦定理,得
[cosθ=b2+a2-a-b22ba=b2-166b].
所以[13b][=b2-166b],解得[⇒][b=32].
故答案为[32].
2. 两向量平行与垂直的充要条件
例2 (全国乙卷·文13)已知向量[a=2,5],[b=λ,4],若[a∥b],则[λ]的值为 .
分析:对于非零向量的平行问题,可以利用向量平行基本定理、向量平行的充分必要条件的坐标关系、基本定理转化为坐标关系“系数比相等”、方向向量转化为直线斜率问题求解.
解法1:因为非零向量[a∥b],
所以存在唯一实数[k],使得[a=kb].
因为[a=2,5],[kb=kλ,4k],所以[2=kλ,5=4k.]
消去参数[k],得[λ=85].
解法2:因为[a=2,5,b=λ,4],[a∥b],
所以[2 · 4-λ · 5=0]. 解得[λ=85].
解法3:不妨设非零向量[a=x1,y1],[b=x2,y2].
因为[a∥b],所以存在唯一实数[t],使得[a=tb].
则有[x1=tx2]且[y1=ty2].
所以[t=x1x2=y1y2],即互相平行的非零向量[a,b]的横坐标之比与纵坐标之比相等.
因为[a=2,5,b=λ,4],[a∥b],
所以[2λ=54],解得[λ=85].
解法4:设非零向量[a=x1,y1],[b=x2,y2],[a∥b],
将解法3得到的结论[t=x1x2=y1y2]变形为[x1y1=][x2y2],得到非零向量[a]的横、纵坐标之比与非零向量[b]的横、纵坐标之比相等.
因为[a=2,5,b=λ,4],[a∥b],
所以[25=λ4],解得[λ=85].
解法5:不妨设向量[a]∥[l1],向量[b]∥[l2].
因为[a=2,5,b=λ,4],
所以[kl1=52],[kl2=4λ].
由[a∥b],得[l1∥l2],即[kl1=kl2].
所以[?52=4λ],解得[λ=85].
例3 (全国甲卷·理14)已知向量[a=3,1],[b=1,0,c=a+kb]. 若[a⊥c],则[k]的值为 .
分析:此题涉及向量的坐标运算,可以利用两种思路求解. 一种思路是利用两个向量垂直的坐标关系,即将位置关系转化为数量积进行运算. 先算出[c=a+kb]的坐标,再由两个非零向量垂直的充要条件的坐标形式解得. 另一种思路是将两个非零向量垂直拓展为直线方向向量垂直,过渡到方向向量所表示的直线垂直,转化到直线斜率乘积为[-1]进行求解.
解法1:因为[a=3,1,b=1,0],
所以[c=a+kb=3+k,1].
因为[a⊥c],
所以[a · c=33+k+1×1=0],解得[k=-103].
故答案为[-103].
解法2:不妨设向量[c]∥[l1],向量[a]∥[l2].
因为[c=a+kb=3+k,1],
所以[kl1=13+k],[kl2=13].
由[a⊥c],得[l1⊥l2].
所以[kl1kl2=13+k · 13=-1],解得[k=-103].
故答案为[-103].
例4 (全国乙卷·理14)已知向量[a=1,3],[b=3,4],若[a-λb⊥b],则[λ]的值为 .
分析:此题的解法与例3类似. 可以利用两个向量垂直的坐标关系,将位置关系转化为数量积进行运算,由两个非零向量垂直的充要条件的坐标形式解得,也可以转化到直线斜率乘积为[-1]进行求解.
解法1:因为[a-λb=1,3-λ3,4=1-3λ,3-4λ],[a-λb⊥b],
所以[31-3λ+43-4λ=0],解得[λ=35].
故答案为[35].
解法2:不妨设向量[a-λb]∥[l1],向量[b]∥[l2].
因为[a-λb=1,3-λ3,4=1-3λ,3-4λ],
所以[kl1=3-4λ1-3λ],[kl2=43].
由[a-λb⊥b],得[l1⊥l2].
所以[kl1kl2=3-4λ1-3λ · 43=-1],解得[λ=35].
故答案为[35].
3. 平面向量的数量积
例5 (全国新高考Ⅱ卷·15)已知向量[a+b+][c=0],[a=1],[b=c=2],则[a · b+b · c+c · a]的值为 .
分析:此题考查了三个非零向量的数量积问题,在未知向量夹角的情况下,要充分利用向量的代数属性解题. 可以通过[a+b+c=0]两边平方,一次性构造[a · b+b · c+c · a];也可以通过[a+b=-c]两边平方,构造[a · b]. 依此类推,构造[b · c],[c · a]的形式,或通过[a · b+b · c+c · a]的结构变形,整体代换求出结果.
解法1:因为[a+b+c=0],
所以[a+b+c2=a2+b2+c2+2a · b+2b · c+2a · c=0],
解得[a · b+b · c+c · a=-92].
解法2:由[a+b+c=0],得[a+b=-c].
所以[a+b2=c2],即[a2+2a · b+b2=c2].
解得[a · b=-12].
由[a+c=-b],得[a+c2=b2],即[a2+2a · c+c2=b2].
所以[a · c=-12].
由[b+c=-a],得[b+c2=a2],即[b2+2b · c+c2=a2].
所以[b · c=-72].
综上可得[a · b+b · c+c · a=-92].
解法3:因为[a · b+b · c=ba+c=-b2=-4],
[a · b+c · a=ab+c=-a2=-1],
[b · c+c · a=cb+a=-c2=-4],
所以[a · b+b · c]+[a · b+c · a]+[b · c+c · a]=[2a · b+b · c+c · a=-9].
所以[a · b+b · c+c · a=-92].
例6 (浙江卷·3)已知非零向量[a,b,c],则“[a · c=b · c]”是“[a=b]”的( ).
(A)充分不必要条件
(B)必要不充分条件
(C)充分必要条件
(D)既不充分也不必要条件
分析:此题考查的知识点为非零向量的数量积与充要条件判断,对学生数量积公式及几何意义理解要求较高,同时注重条件命题的充分性和必要性的判断. 考虑两者之间的推出关系后,可以得到两者之间的条件关系.
解法1:充分性证明.
因为[a · c=b · c],
所以[accosa,c=bccosb,c],非零向量[a,b,c],[c≠0].
所以[acosa,c=bcosb,c].
说明向量[a,b]在向量[c]上的投影相等,不一定有[a=b],即“[a · c=b · c]” “[a=b]”.
所以“[a · c=b · c]”是“[a=b]”的不充分条件.
必要性证明.
由[a=b],则[a · c=b · c]成立,即“[a · c=b · c]”[⇐]“[a=b]”.
故“[a · c=b · c]”是“[a=b]”的必要条件.
综上所述,“[a · c=b · c]”是“[a=b]”的必要不充分条件.
故答案选B.
解法2:记[a=OA],[b=OB],[c=OC],[θ1=a,c],[θ2=b,c],如图2所示.
[O][A][B][C] [图2]
由图2,知[a · c=b · c][⇒][acosθ1=bcosθ2] [a=b].
因为[a=b][⇒][a · c=b · c],
所以[a · c=b · c] [a=b],[a · c=b · c][⇐][a=b].
綜上所述,“[a · c=b · c]”是“[a=b]”的必要不充分条件.
故答案选B.
例7 (北京卷·13)已知向量[a,b,c]在正方形网格中的位置如图3所示. 若网格纸上小正方形的边长为1,则[a+b · c]的值为 ;[a · b]的值为 .
答案:0;3.
分析:此题考查向量坐标表示的加法运算、数量积的运算,试题难度不大,要求学生计算细心. 对于[a+b · c],可以先进行向量和的运算,再进行向量的数量积运算;也可以展开为[a · c+b · c],先进行向量数量积运算再求和.
解法1:因为[a=2,1],[b=2,-1],
所以[a+b=4,0],[a · b=2×2+1×∙-1=3].
因为[c=0,1],
所以[a+b · c=0].
解法2:因为[a=2,1],[b=2,-1],[c=0,1],
所以[a+b · c=a · c+b · c=1+-1=0],
[a · b=2×2+1×∙-1=3].
例8 (上海卷·4)如图4,正方形[ABCD]的边长为[3],则[AB · AC]的值为 .
[A][D][C][B][图4]
分析:此题考查向量的数量积,可以从向量数量积的定义、向量的坐标运算(即向量的代数属性)、向量加法的三角形法则、向量投影等几个方面的向量的几何属性进行解题,试题较易,切入点较多,不同层次的学生均可得分.
解法1:已知正方形[ABCD]的边长为[3],
则[AB=3],[AC=32],[AB, AC=45°],
所以[AB · AC=ABACcos45°=3×32×22=9].
故答案为[9].
解法2:建立如图5所示的平面直角坐标系.
[O(A)][D][C][B] [x][y][图5]
则[A0,0],[B3,0],[C3,3],[D0,3],
则[AB=3,0],[AC=3,3],
所以[AB · AC=3×3+3×0=9].
故答案为[9].
解法3:由向量加法的三角形法则,得[AC=AB+BC],
因为[AB⊥BC],
所以[AB · BC=0],
所以[AB · AC=AB · AB+BC=AB2+AB · BC=AB2=9].
故答案为[9].
解法4:由图3知,[AC]在[AB]方向上的投影为[ACcosAB, AC=AB],
由向量[AB]与[AC]数量积的几何意义,知[AB · AC]等于向量[AC]在[AB]方向上的投影与[AB]的乘积.
所以[AB · AC=ABACcosAB, AC=AB2=9].
故答案为[9].
4. 平面向量基本定理的应用
例9 (全国新高考Ⅰ卷·12)在正三棱柱[ABC-A1B1C1]中,[AB=AA1=1],点[P]满足[BP=λBC+μBB1],其中[λ∈0,1],[μ∈0,1],则( ).
(A)当[λ=1]时,[△AB1P]的周长为定值
(B)当[μ=1]时,三棱锥[P-A1BC]的体积为定值
(C)当[λ=12]时,有且仅有一个点[P],使得[A1P⊥BP]
(D)当[μ=12]時,有且仅有一个点[P],使得[A1B⊥⊥]平面[AB1P]
分析:此题立足于立体几何,对向量问题的考查比较深入. 从平面向量基本定理出发,充分利用向量加法的平行四边形法则的几何属性,将动点转化到定直线,结合空间直角坐标系进行求解.
解:点[P]在矩形[BCC1B1]的内部(含边界).
对于选项A,当[λ=1]时,[BP=BC+μBB1=BC+][μCC1],即此时点[P]的轨迹为线段[CC1],[△AB1P]的周长不是定值,故选项A错误;
对于选项B,当[μ=1]时,[BP=λBC+BB1=BB1+][λB1C1],故此时点[P]的轨迹为线段[B1C1]. 而[B1C1∥][BC],所以[B1C1∥]平面[A1BC]. 则有点[P]到平面[A1BC]的距离为定值. 所以其体积为定值. 故选项B正确.
对于选项C,当[λ=12]时,[BP=12BC+μBB1],取线段[BC]和[B1C1]的中点,分别记为[Q,H],则[BP=][BQ+μQH],所以点[P]的轨迹为线段[QH]. 建立空间直角坐标系,如图6所示,则[A132,0,1],[P0,0,μ],[B0, 12,0],因此可以得到[A1P=-32,0,μ-1],[BP=0,-12,μ]. 由[A1P⊥BP],得[μμ-1=0]. 解得[μ=0]或[μ=1]. 所以点[H,Q]均满足. 故选项C错误.
[A][B][C][A1][B1][C1][H][z][x
][y
][Q][M][N][图6]
对于选项D,当[μ=12]时,[BP=λBC+12BB1]. 取线段[BB1]和[CC1]的中点,分别记为点[M,N],如图5所示. 因为[BP=BM+λMN],所以点[P]的轨迹为线段[MN]. 设[P0,y0, 12]. 因为[A32,0,0],所以[AP=][-32,y0, 12],[A1B=-32, 12,-1]. 由[A1B⊥AP],得[34+][12y0-12=0],即[y0=-12]. 此时点[P]与点[N]重合. 故选项D正确.
综上所述,答案选BD.
三、试题解法赏析
例10 (全国新高考Ⅰ卷·10)已知点[O]为坐标原点,点[P1cosα,sinα,P2cosβ,-sinβ,P3cosα+β,sinα+β],[A1,0],则( ).
(A)[OP1=OP2]
(B)[AP1=AP2]
(C)[OA · OP3=OP1 · OP2]
(D)[OA · OP1=OP2 · OP3]
分析:此题考查向量的代数属性(即坐标运算),对于选项A和选项B写出[OP1],[OP2],[AP1],[AP2]的坐标,利用坐标公式求模,即可判断正误. 对于选项C和选项D,根据向量的坐标,应用向量数量积的坐标表示及两角和差公式化简,即可判断正误. 此题还可以通过向量的几何属性,在单位圆中构造[α,β,-β,α+β]等角度,结合向量的数量积定义得出答案,难点在于图形的构造.
解法1:对于选项A. 因为[OP1=cosα,sinα],[OP2=][cosβ,-sinβ],所以[OP1=cos2α+sin2α=1],[OP2=][cosβ2+-sinβ2=1]. 所以[OP1=OP2]. 故选项A正确.
对于选项B. 因为[AP1=cosα-1,sinα],[AP2=][cosβ-1,-sinβ],所以[AP1=cosα-12+sin2α=][cos2α-2cosα+1+sin2α=21-cosα=4sin2α2=2sinα2.]同理,[AP2=cosβ-12+sin2β=2sinβ2]. 所以[AP1,][AP2]不一定相等. 故选项B错误.
对于选项C. 由题意,得[OA · OP3=1 · cosα+β+][0 · sinα+β=cosα+β, OP1 · OP2=cosαcosβ+sinα ·][-sinβ]=[cosα+β]. 故选项C正确.
对于选项D. 由题意,得[OA · OP1=1 · cosα+0 ·][sinα=cosα, OP2 · OP3=cosβcosα+β+-sinβsinα+β=][cosαcos2β-sinαsinβcosβ-sinαsinβcosβ-cosαsin2β=][cosαcos2β-sinαsin2β=cosα+2β]. 故选项D错误.
综上所述,答案选AC.
解法2:因为[P1cosα,sinα],[P2cosβ,-sinβ],[P3cosα+β,sinα+β],[A1,0],所以[OP1=OP2=][OP3=OA1=1],易知[P1,P2,P3,A]四点在单位圆上. 建立如图7所示的平面直角坐标系,则有[∠AOP1=α],[∠AOP2=∠P1OP3=β],则[OA, OP1=α],[OA, OP3=][α+β],[OP1, OP2=α+β],[OP2, OP3=α+2β]. 所以[OP1=OP2=1]. 故选项A正确.
[A][x][O][y][P1][P3][P2][图7]
对于选项B. 在[△AOP1]中,[OA=OP1=1],[∠AOP1=][α]. 由余弦定理,得[AP12=OA2+OP12-2OAOP1cosα].所以[AP1=2-2cosα=2sinα2]. 在[△AOP2]中,[OA=][OP2=1,∠AOP2=β],由余弦定理,得[AP22=OA2+][OP22-2OAOP2cosβ],所以[AP2=2-2cosβ=2sinβ2]. 由此可得[AP1, AP2]不一定相等. 故选项B错误.
对于选项C. [OA · OP3]=[OAOP3cosOA, OP3]=[cosα+β]. [OP1 · OP2=OP1OP2cosOP1, OP2=cosα+β.]可得[OA · OP3=OP1 · OP2]. 故选项C正确.
對于选项D. [OA · OP1=OAOP1cosOA, OP1=cosα,][OP2 · OP3=OP2OP3cosOP2, OP3=cosα+2β],可得[OA · OP1]与[OP2 · OP3]不一定相等. 故选项D错误.
综上所述,答案选AC.
例11 (天津卷·15)在边长为[1]的等边三角形[ABC]中,点[D]为线段[BC]上的动点,[DE⊥AB]且交[AB]于点[E],[DF∥AB]且交[AC]于点[F],则[2BE+DF]的值为 ,[DE+DF · DA]的最小值为 .
分析:此题将平面向量的模和向量的数量积进行综合考查. 一种思路是通过向量的坐标运算的代数属性进行求解;另一种思路是通过向量的几何属性进行求解.
解法1:建立如图8所示的平面直角坐标系.
[O(B)][D] [C][F][E][A][x][y][图8]
则[B0,0],[A12, 32],[C1,0].
设[Dt,0]([0<t<1]),则[DC=1-t].
在[Rt△BED]中,[BE=t2],则[Et4, 3t4].
在正三角形[DFC]中,[DF=DC=1-t],
则[Ft+12, 31-t2].
因为[BE=t4, 3t4],[DF=1-t2, 31-t2],
所以[2BE+DF=12, 32].
则[2BE+DF=122+322=1].
故第一小空答案为[1].
因为[DE=-3t4, 3t4],[DF=1-t2, 31-t2],[DA=1-2t2, 32],
所以[DE+DF=2-5t4, 23-3t4].
所以[DE+DF · DA]
[=2-5t41-2t2+3223-3t4]
[=5t2-6t+44]
[=54t2-32t+1]
[=54t-352+1120].
当[t=35]时,有[DE+DF · DAmin=1120].
故第二小空答案为[1120].
解法2:如图9,过点[F]作[FQ⊥AB]交[AB]于点[Q]. 连接[AD].
[B][D] [C][F][A] [Q][E][图9]
不妨设[BE=λBA],[λ∈0,1].
则[BE=λ],[EA=1-λ],[BD=2λ],[ED=3λ].
在[Rt△AQF]中,[QF=ED=3λ],[∠AFQ=30°].
所以[QA=QFtan30°=λ, AF=2QA=2λ, DF=][AE-AQ=1-2λ].
因为[BE],[DF],[AB]共线,
所以[2BE+DF=2BE+DF=2λ+1-2λ=1].
故第一小空答案为[1].
由题意,知[DE+DF · DA=DE · DA+DF · DA].
因为在[Rt△ADE]中,[DE⊥EA],[DA=DE+EA],
所以[DE · DA=DE · DE+EA=DE2+DE · EA=][3λ2+0=3λ2].
在[△ADF]中,因为[FD · FA=120°],[DA=DF+FA],
所以[FD · FA=FDFAcos120°=1-2λ2λ-12=][2λ2-λ],
所以[DF · DA=DF · DF+FA=DF2+DF · FA=][1-2λ2-2λ2-λ=2λ2-3λ+1].
综上所述,[DE+DF · DA=DE · DA+DF · DA=][5λ2-3λ+1=5λ-3102+1120].
当[λ=310]时,有[DE+DF · DAmin=1120].
故第二小空答案为[1120].
例12 (浙江卷·17)已知平面向量[a,b,c c≠0]满足[a=1],[b=2],[a · b=0],[a-b · c=0]. 记平面向量[d]在[a,b]方向上的投影分别为[x,y],[d-a]在[c]方向上的投影为[z],则[x2+y2+z2]的最小值为 .
分析:此题将平面向量问题与不等式问题进行综合,通过向量的坐标运算的代数属性,将向量转化为三元问题求最值. 最值问题的求解可以从代数、几何两个方向切入,对学生要求较高. 一种思路是利用柯西不等式求解;另一种思路是将三元问题放到空间图形中转化为距离问题求解.
解法1:设[a=1,0,b=0,2,c=m,n],
则[a-b · c=m-2n=0],即[m=2n].
因为向量[d]在[a,b]方向上的投影分别为[x,y],
所以[d=x,y].
所以向量[d-a]在向量[c]方向上的投影[z=d-a · cc=][mx-1+nym2+n2=2x-2+y5],即[2x+y-5z=2].
由柯西不等式,得
[x2+y2+z2]
[=11022+12+-52x2+y2+z2]
[≥1102x+y-5z2]
[=25].
当且仅当[x2=y1=z-5,2x+y-5z=2]时,等号成立.
解得[x=25,y=15,z=-55.]
所以[x2+y2+z2]的最小值为[25].
故答案为[25].
解法2:设[a=1,0,b=0,2,c=m,n],
则[a-b · c=m-2n=0],即[m=2n].
因为向量[d]在[a,b]方向上的投影分别为[x,y],
所以[d=x,y].
所以向量[d-a]在向量[c]方向上的投影[z=d-a · cc=][mx-1+nym2+n2=2x-2+y5],即[2x+y-5z=2].
建立如图10所示的空间直角坐标系.
[A][O][C][B] [y][z][x] [图10]
由几何意义,知[2x+y-5z=2]表示平面[ABC],[x2+y2+z2]表示面内动点[Px,y,z]到点[O0,0,0]的距离,即[x2+y2+z2min]为点[O]到平面[ABC]的距离的平方,记为[x2+y2+z2min=h2OP].
因为[A1,0,0],[B0,0,-255],[C0,2,0],
则[AB2=1+0+2552=95,AC2=1+22+0=5,BC2=][0+22+2552=245].
由余弦定理,得[cos∠ABC=AB2+BC2-AC22AB · BC=69].
所以[sin∠ABC=1-cos2∠ABC=539].
所以[S△ABC=12 · AB · BC · sin∠ABC=2].
因為[S△AOB=12OA · OB=55],[hOC=2],
所以[VO-ABC=VC-AOB],即[13S△ABChOP=13S△AOBhOC].
所以[13 · 2 · hOP=13 · 55 · 2],解得[hOP=105].
所以[x2+y2+z2min=h2OP=25].
故答案为[25].
参考文献:
[1]中华人民共和国教育部制定. 普通高中数学课程标准(2017年版2020年修订)[M]. 北京:人民教育出版社,2020.
[2]陈利民. 2020年高考“平面向量”专题解题分析[J]. 中国数学教育(高中版),2020(10):9-13.

