Further Discussion for Generalized Normal Sectors in Class II

Wang Zhaoxia

(School of Mathematical Sciences,University of Electronic Science and Technology of China,Chengdu 611731,China)

Abstract Generalized normal sectors are developed from normal sectors to study the existence and the number of orbits connecting with an equilibrium along an exceptional direction.At present,there are no clear results about the conditions that a unique or infinitely many orbits connect the equilibrium in a generalized normal sector of class II.We give a necessary and sufficient condition to distinguish these two cases.In addition,we also give two sufficient conditions for the nonexistence of orbits connecting with the equilibrium in an open quasi-sectorial region which may not be a generalized normal sector.

Key words Degenerate equilibrium Exceptional drection Generalized normal sector Qualitative theory

1 Introduction

The qualitative theories of differential equations have attracted a lot of attention.One can study some special and important orbits(equilibria,closed orbits,etc.) and investigate the orbits near them to get the global phase diagram.For a planar analytic differential system

a point(x0,y0)is called an equilibrium ifP(x0,y0)=Q(x0,y0)=0.Moreover,the isolated equilibrium(x0,y0)is said to be non-degenerate if the determinant of the Jacobian matrix for system(1.1)at(x0,y0)

Otherwise,it is said to be degenerate.The qualitative properties at non-degenerate equilibria are well known,see [1,3] and references therein.Even when an equilibrium point is degenerate,but the linear parts are not identically zero,the qualitative properties are completely shown in [2,10].However,for an equilibrium whose linear parts are identically zero,there will be a lot of difficulties in studying the distribution of orbits nearby.

In Poincaré’s view,a degenerate equilibrium is composed of several simple equilibria.One of the most important methods to analyze higher order degenerate equilibria is blowing up[4].In general,the higher degree of degeneracy is,the more times the blowing-up transformation is used.The blowing-up technology may be invalid when the lowest degree at an equilibrium is undefined.Another method to discuss orbits connecting with a degenerate equilibrium is to divide its small neighbourhood into a finite number of sectors.

Consider the differential system

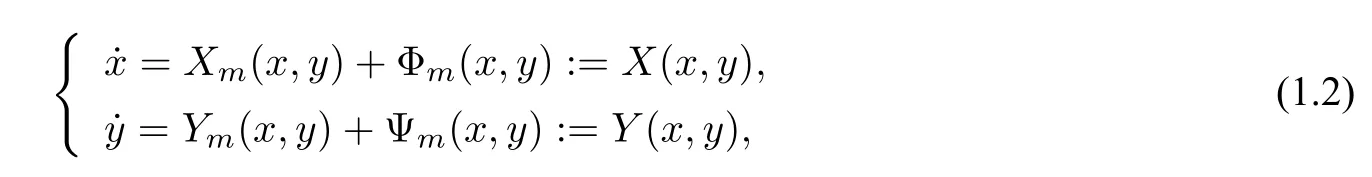
whereXm(x,y)andYm(x,y)are homogeneous polynomials of degreem ≥1,Φm(x,y),Ψm(x,y)are both analytic near the origin,and Φm(x,y)=o(rm),Ψm(x,y)=o(rm)asr=→0.HereXm(x,y)orYm(x,y)can be identically zero.LetO:=(0,0)be an isolated equilibrium of system(1.2).In polar coordinatesx=rcosθandy=rsinθ,system(1.2)can be written in the form

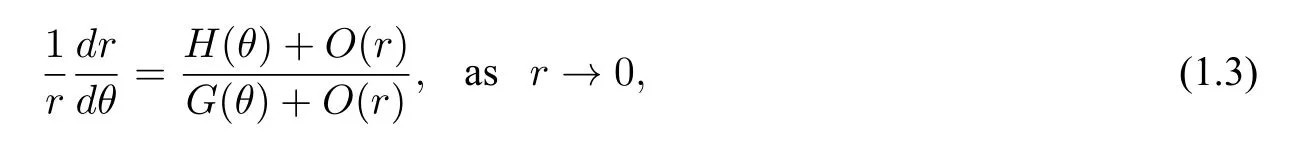
where

The direction of the polar angle,θ0(0≤θ0<2π) is called an exceptional direction if there exists a sequence of pointsPn:=(rn,θn)such thatθn →θ0,rn →0,tanαn →0 asn →∞,whereαnis the angle turning anti-clockwise from the directionθnto the field vector atPn.For an isolated equilibrium of an analytic system,if there are orbits connecting with the equilibrium,they can only enter or leave it helically or along exceptional directions.As shown in[7,10],exceptional directions are determined by zeros ofG(θ).

The Z-sectors[6]are the ones which are obtained by using the branches ofZ(x,y) :=xX(x,y)+yY(x,y)=0 to slice a small neighbourhood ofO.A Z-sector contains at most a finite number of exceptional directions and the two edges of a Z-sector are both without contact.Some results[6,7]were given to investigate the orbits connecting withOin a Z-sector.But sometimes Z-branches ofZ(x,y)=0 are difficult to calculate.The normal sectors [7,10] are circular sectors with vertex at the equilibriumO.In a normal sector,at most one exceptional direction exists,the field vector is not orthogonal to the radius vector and the two edges of the sector are both without contact.But it is hard to construct a norm sector when the exceptional directionθsatisfiesH(θ)=0.The generalized normal sectors[8]are developed from normal sectors,which do not restrict edges of the sectors to be radial lines.The concept of generalized normal sectors was first proposed by Tang and Zhang[8]in which they classified generalized normal sectors into three types and gave the complete orbit distribution in generalized normal sectors of class I.Later,Tang,Li and Zhang[9]gave a sufficient and necessary condition for the existence of orbits connecting withOin generalized normal sectors of class III.For generalized normal sectors of class II,a sufficient condition for the uniqueness of orbits connecting withOwas obtained by Jia,Chen and Chen[5].But the orbit distribution in generalized normal sectors of class II is not certain enough.

The organization of this paper is as follows.In Section 2 we introduce the method of generalized normal sectors and some criterions to determine how many orbits connect withOin generalized normal sectors.We devote Section 3 to further discussion the number of orbits connecting withOin generalized normal sectors of class II and give a sufficient and necessary condition for the uniqueness of orbits connecting withO.An example to show the qualitative properties of equilibria at infinity is studied in Section 4.

2 Preliminaries

Figure 1 Three classes of GNS

For each class of GNS,[8] gave one criterion to determine the existence and the number of orbits connectingO.

Figure 2 The GNS △in class III for r˙ < 0

Until now,only the number of orbits connecting theOin GNS of class II has a small gap.

3 Main results

Figure 3 The GNS △ in class II for r˙ < 0

4 Applications

Consider the qualitative properties of equilibria at infinity for system

In fact,the bifurcation diagram and global phase portraits have been studied in [5].Here we use the theorems in section 3 to verify the number of orbit connecting the equilibria at infinity.

By the Poincaré transformationsx=1/z,y=u/zandx=v/z,y=1/z,system (4.6) can be rewritten as

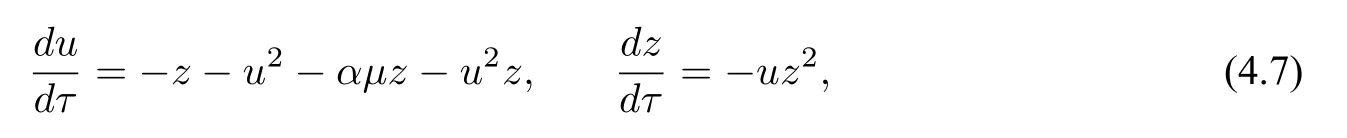
and

wheredτ=dt/z.Obviously,system(4.7)has a unique equilibriumA:=(0,0)on theu-axis which is nilpotent andB:=(0,0)is a non-degenerate equilibrium of system(4.8).

Taking the polar coordinatesx=rcosθandy=rsinθ,system(4.7)becomes(1.3),whereG(θ)=sin2θandH(θ)=−cosθsinθ.The equationG(θ)=0 has exactly two real roots 0 andπon the interval[0,2π).Moreover,G(0)=H(0)=G(π)=H(π)=0.

Figure 4 Dynamical behaviors near A

ThenBis an unstable unidirectional node by[10,Chapter 2].The properties of equilibria at infinity of for system(4.6)are shown in Figure 5.

Figure 5 Dynamical behaviors near equilibria at infinity

Remark 1Theorem 3.1 tells us that if in a GNS of class II there are infinitely many orbits connecting with the equilibrium,it must contain a GNS of class I whose edges are not orbits.

Remark 2Lemma 2.5 does provide two conditions that no GNS of class I with non-orbital edges is included in a GNS of class II.In the above simple example,one can also get the uniqueness of orbits connectingAinby Lemma 2.5.