一类具有非线性扰动的新冠肺炎SIRC 随机模型研究

金薇 廖新元 骆金鹏 杨永丽

（南华大学数理学院,衡阳,421001）

1 引言

2019 年12 月发现的新冠肺炎病毒是目前已知的第7 种可以感染人的冠状病毒.它以一种惊人的速度在中国各省份和全世界迅速蔓延,研究人员建立数学模型研究疾病的传播机制并给出疫情的防控措施[1,2].考虑到降水量、温度、湿度等诸多环境因素对传染病的传播都有重大的影响,因此,我们认为随机微分方程模型相比于确定性模型,能更好地描述传染病的传播机制[3,4].目前,在随机微分方程中引入白噪声的方法有两种：一是加入与系统状态成正比的随机扰动项[5,6,7],二是加入与系统变量呈现非线性关系的随机扰动项[8,9].

根据传染病的传播规律,人群可被分为四个部分：易感者、感染者、恢复者、交叉免疫者,在时刻t各部分的人数分别以S(t),I(t),R(t),C(t)来表示.S(t)与C(t)的区别在于是否存在免疫个体差异,当不存在此类免疫差异时,SIRC 模型即是SIRI 模型.S(t)+I(t)+R(t)+C(t)表示人群的个体总数.本文通过加入非线性随机扰动项改进文献[10]的模型,得到如下的新冠肺炎SIRC 随机模型:

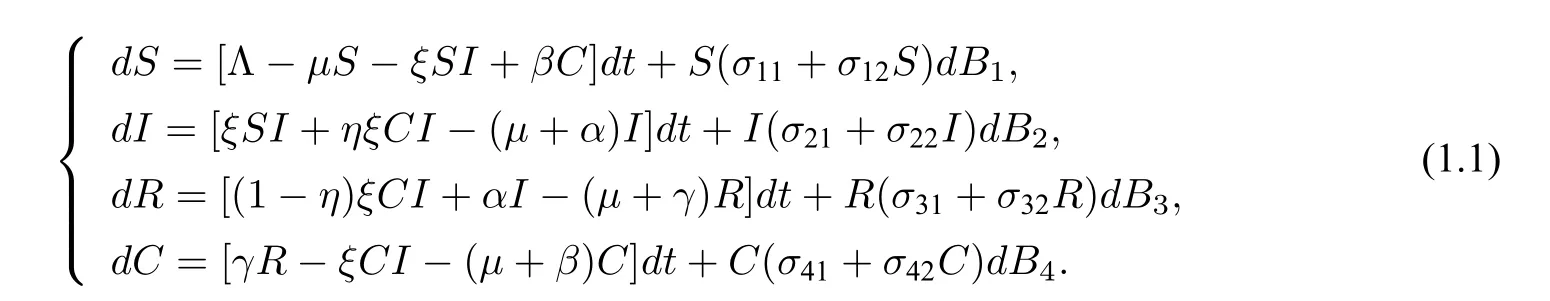
其中Λ 和µ分别表示出生率和死亡率,η表示交叉免疫体的平均再感染率,α表示感染者的恢复率,β表示交叉免疫体再次易感的比率,γ表示恢复者变为交叉免疫者的比率,ξ表示接触率,σij(i,j=1,2,3,4)表示随机干扰的强度.假设模型(1.1)定义在具有滤子{Ft}t≥0且满足通常条件（滤子递增且右连续,F0包含所有P零集）的完备概率空间(Ω,F,{Ft}t≥0,P)上.

2 疾病的随机持久性和平稳分布

2.1 疾病的随机持久性

2.2 疾病的平稳分布

3 疾病灭绝性

4 数值模拟

本节利用Milstein 数值模拟仿真([16])验证本文的主要结果.参照文献[17,18,19,20,21]对系统(1.1)定义参数如下：S(0)=0.6,I(0)=0.2,R(0)=0.11,C(0)=0.09,θ=0.4.

4.1 疾病平稳分布模拟

1.取Λ=0.07,µ=0.1,ξ=0.66,α=0.1,β=0.05,η=0.08,γ=0.19,v11=0.03,v12=0.02,v21=0.06,v22=0.04,v31=0.22,v32=0.22,v41=0.02,v42=0.02,Rs0=0.893<1,结果如图1 所示.

2.取Λ=0.07,µ=0.08,ξ=0.66,α=0.15,β=0.05,η=0.08,γ=0.19,v11=0.1,v12=0.02,v21=0.06,v22=0.04,v31=0.22,v32=0.22,v41=0.32,v42=0.32=1.458>1,结果如图2 所示.

图1 表示在1 时,经过一段时间疾病会达到平稳分布.图2 表示在1 时,经过一段时间疾病不会达到平稳分布,这与定理2.2 的结论相符.

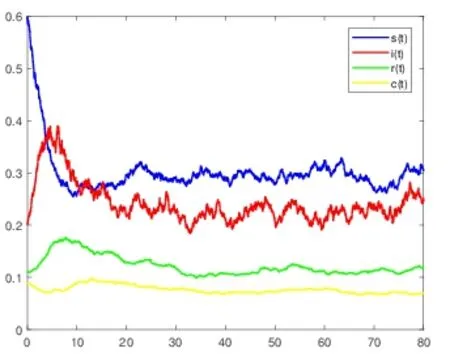
图1 疾病持久且平稳分布图

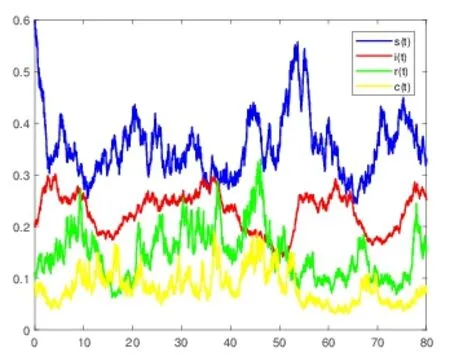
图2 疾病持久且不平稳分布图

4.2 疾病灭绝和不同噪声强度下感染者人数变化的情况模拟

3.取Λ=0.07,µ=0.3,ξ=0.25,α=0.18,β=0.02,η=0.38,γ=0.04,v11=0.4,v12=0.2,v21=0.3,v22=0.4,v31=0.3,v32=0.4,v41=0.1,v42=0.3=0.497<1,结果如图3 所示.

4.取Λ=0.07,µ=0.3,ξ=0.25,α=0.2,β=0.2,η=0.28,γ=0.39,三条曲线i1,i2,i3分别表示在不同强度的干预措施下感染者的变化趋势,随机变量参数取值如下：

曲线i1:随机扰动为零,即是确定性模型,v11=0,v12=0,v21=0,v22=0,v31=0,v32=0,v41=0,v42=0.

曲线i2:随机扰动较小,v11=0.1,v12=0.2,v21=0.1,v22=0.2,v31=0.1,v32=0.1,v41=0.2,v42=0.2.

曲线i3:随机扰动较大,v11=0.7,v12=0.5,v21=0.5,v22=0.6,v31=0.6,v32=0.6,v41=0.8,v42=0.5.

图3 表示在1 时,疾病趋于灭绝,这与定理3.1 的结论相符.图4 表示干扰强度越大,疾病灭绝的时间越短,这说明强力的干扰措施有利于疾病的防控.

图3 疾病灭绝图

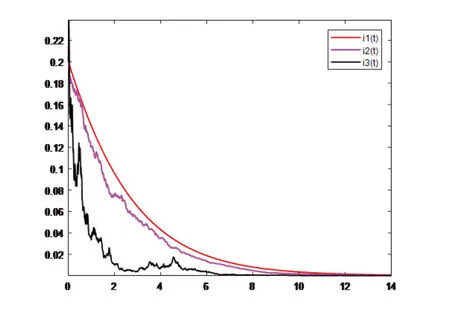
图4 不同噪声强度下感染者人数的变化图

5 结论

本文考虑到随机变量可能与系统变量存在非线性关系,引入了非线性随机扰动项到传统的SIRC 传染病模型[10].通过构建合适的Lyapunov 函数,我们得到系统(1.1)具有随机最终有界性和随机持久性的充分条件;通过引入参数和,我们给出了系统(1.1)存在唯一遍历平稳分布和疾病灭绝的相关结论：类似于基本再生数的性质,若1,则疾病存在平稳分布,若1,则疾病不存在平稳分布,将会流行传播,若1,则疾病将会趋于灭绝;我们还通过分析不同噪声强度下感染者人数的变化趋势发现：干扰措施越大越有利于疾病的防控.