Existence of Positive Solutions for a Critical Kirchhoff Type Equation with a Sign Changing Potential

Yang Liu Wang Lixiong

(1.College of Mathematics and Statistics,Hengyang Normal University,Hengyang 421008,Hunan,China;2.School of Mathematics and Statistics,Central South University,Changsha 410083,Hunan,China)

Abstract In this paper,we investigate a class of Kirchhoff type problem involving a critical nonlinearitywhere Ω is a smooth bounded domain in RN(N≥3),a,b,λ > 0 and g(x)is a sign-changing potential,g ∈L∞(Ω)with the set{x ∈Ω : g(x) > 0}of positive measure.For N=3,we obtain a positive ground state solution to the problem with λ in a small right neighborhood of λ1a.For N=4,under some assumptions on g,we get the existence and non-existence of the positive solutions.For N≥5,by using the variational method,we obtain that the equation has a ground state solution.

Key words Kirchhoff type problem Nehari manifold Ground state solution Critical exponent Variational method

1 Introduction and Main Results

Condider the Kirchhoff type problem:

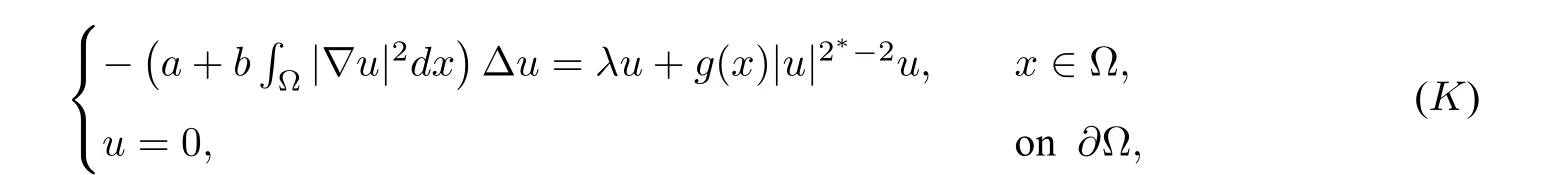
where Ω is a smooth bounded domain in RN(N≥ 3),a,b,λ >0,and the nonlinear growth ofg(x)|u|2∗−2ureaches the Sobolev critical exponent since the critical exponent 2∗=,whereg(x)is a sign-changing potential,andg ∈L∞(Ω)with the set{x ∈Ω:g(x)>0}of positive measure.

Problem(K)is related to the stationary analogue of the Kirchhoff equation which was proposed by Kirchhoff in[1]as a generalization of the D’Alembert wave equation

for free vibrations of elastic strings.Here,ρis the mass density,ρ0is the initial tension,his the area of the cross section,Eis the Young modulus of the material andLis the length of the string.Problem(K)is non local because of the presence of the term−(a+b∫Ω|∇u|2dx),which implies that the equation in(K)is no longer a point-wise identity.Such a phenomenon provokes some mathematical difficulties,which make the study of such a class of problems particularly interesting.Lions[4]introduced an abstract functional analysis framework to the equation

After that there are abundant results about (1.1).Here let us briefly recall some existing results.Perera-Zhang [7] obtained nontrivial solutions of problem (1.1) by the Yang index and critical group;Zhang-Perera[8]considered multiple and sign-changing solutions of problem(1.1)by the invariant sets of descent flow.In particular,when the nonlinearityf(x,u)satisfies critical growth in problem(1.1),some important and interesting results can be found when Ω⊂R3is a smooth bounded domain(see[7–12][26]and the references therein).

Iff(x,u)=λu+g(x)|u|2∗−2u,problem (1.1) becomes problem (K).Letλ1be the principal eigenvalue of(−∆(Ω)),we have the following variational characterization

WhenN≥3,g(x) is a sign-changing potential.The presence of the sign changing potential and critical exponent set obstacles to prove the compactness of problem(K).Hence,it is natural to ask whether problem(K)adimits nontrivial positive solutions?

Motivated by the works described above,particularly,by the results in [7–13,17–20],for the case ofN=3,we try to obtain the existence of positive ground state solutions to problem (K) forλin a small right neighborhood ofλ1a.We do not use the concentration compactness principle.To overcome this difficulty and obtain the desired result,we only use the properties of the Nehari manifold.By the variational method and Mountain Pass Theorem,under some assumptions ong,we consider the existence and non-existence results forN=4 andλbeing different scope.WhenN≥5 we obtain a ground state solution of problem(K)by virtue of the variational method.

The main results are as follows.

Theorem 1.1Suppose thatN=3,a,b >0 andg ∈L∞(Ω)with the set{x ∈Ω :g(x)>0}of positive measure.Let

Then problem(K)has at least one positive ground state solution,whereSis the best Sobolev constant for the embedding of(Ω)inL6(Ω).

Remark 1.1The ground state solution can be obtained by finding the global minimizer of the Nehari manifold.It is easy to see that the Nehari manifold contains every nontrivial solutions of problem (K).Furthermore,since the Sobolev embedding(Ω)6(Ω)is continuous and not compact,to recover the compactness and obtain the solution,we prove that the energy functional satisfies(PS)−condition at the least energy level on a block of the Nehari manifold.We can confirm the ground state solution lying a certain part of the Nehari manifold.

Theorem 1.2LetN=4,g ∈L∞(Ω)with the set{x ∈Ω:g(x)>0}of positive measure.(1)If 0<|g|∞λ1a.(2)If 0bS2andg(x)≡|g|∞,then problem(K)has a positive solution for all 0<λ<λ1a.

Remark 1.2In[5],the casea=1,b=0 andg(x)=1 is considered.In[14],the caseg(x)=µis considered.Theorem1.2 gives an extension of those results to the Kirchhoff type problem for the caseN=4.

Theorem 1.3LetN≥5,g ∈L∞(Ω)with the set{x ∈Ω:g(x)>0}of positive measure.If

then problem(K)has a positive ground state solution for allλ>λ1a.

The rest of this paper is organized as follows.In Section 2,we introduce some notations and prove a useful preliminary lemma.In sections 3-5,we give the proof of Theorem 1.1-Theorem1.3.

2 Preliminaries

In thissection,weintroducesome notationsand prove ausefulpreliminarylemma.

Let the space?(Ω)be equipped with the inner product(u,v)=,and the norm for all(Ω).

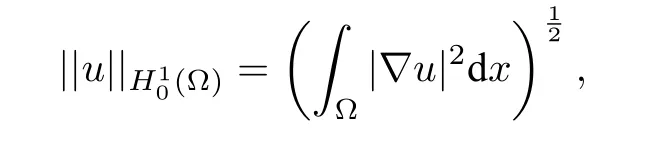
Let|·|pbe the usual Lebesgue spaceLp(Ω)norm;|Ω|be the Lebesgue measure of Ω;Cbe various positive constants.

LetSbe the best Sobolev constant,namely

It is well known thatSis independent of Ω and is never achieved except when Ω=RN.Moreover,Sis achieved by the function

We can also easily get that

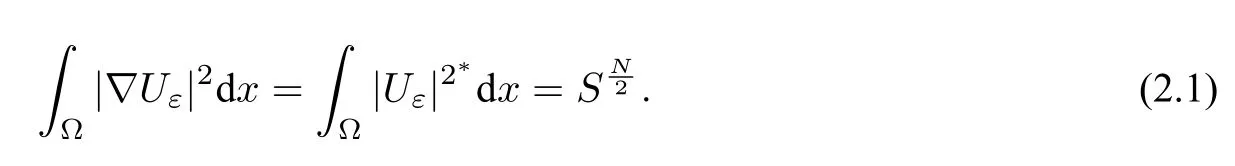
We callu ∈a weak solution of problem(K),ifusatisfies

Applying the usual elliptic regularity theory,we can conclude that every weak solution of problem(K)belongs toC2(Ω).

The energy functional corresponding to problem(K)is given by

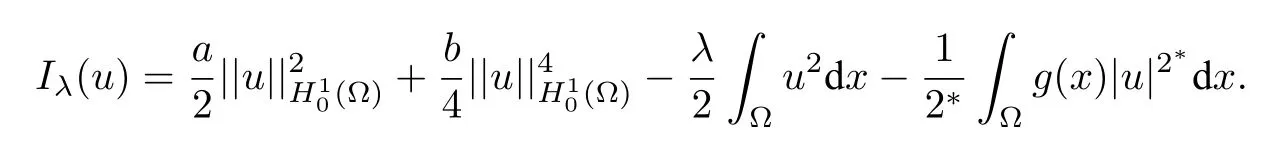
We can easily check thatIλis well-defined and belongs toC1(H01(Ω),R).

Now,we give the following preliminary lemma.

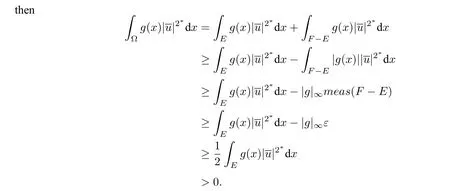
This concludes the proof.

3 Proof of Theorem 1.1

SinceN=3,the energy functionalIλcorresponding to problem(K)is given by

Moreover,we have the following lemma.

4 Proof of Theorem 1.2

In this section,we introduce a complete description of thePSsequences to understand their features more clearly and give the proof to Theorem 1.2.

SinceIλis aC1functional on(Ω),we see thatu∗is a solution of problem(K).By the strong maximum principle,it follows thatu∗is a positive solution of problem(K).SinceIλ(u∗)=m,u∗is a positive ground state solution.This completes the proof of theorem 4.1.

Theorem 4.2LetN=4 and 0<|g|∞

ProofSuppose(Ω) is a nontrivial solution of problem (K).By virtue of the Sobolev inequality,we have

Note that 0<|g|∞≤bS2and 0<λ≤λ1a,we obtainu=0.This yields a contradiction.

With no loss of generality we assume 0∈Ω.Owing to[23],we introduce the Talenti function cut-off appropriately([24]),

whereε >0 and(Ω)is an appropriate cut-off function such thatψ ∈[0,1]andψ=1 on some neighborhood of 0.

Let

then we have the following estimate:asε →0

whereC >0 is some constant.

The next lemma will confirm a mountain pass level ofIλ,which is below the desired energy level.

Lemma 4.1Suppose that|g|∞>bS2andg(x)≡|g|∞hold.Then there exists a constantC1>0 such that

for allε ∈(0,C1).

ProofBy the assumption and(4.9),for allt≥0,we have

Thus there exists a constantC1>0 such that

for allε ∈(0,C1).

Now we give the proof to Theorem 1.2.

Proof of Theorem 1.2According to Theorem 4.1 and 4.2,we only need to consider the case of Theorem 1.2(3),where|g|∞>bS2andg(x)=|g|∞,In this case,we apply the mountain pass theorem([6]).As usual,we need to ensure the mountain pass geometry ofIλ,that isIλ(0)=0 and

By applying the mountain pass theorem,the usual elliptic regularity theory and the strong maximum principle,we can conclude that the solution of problem (K) is positive,which completes the proof of Theorem 1.2(3).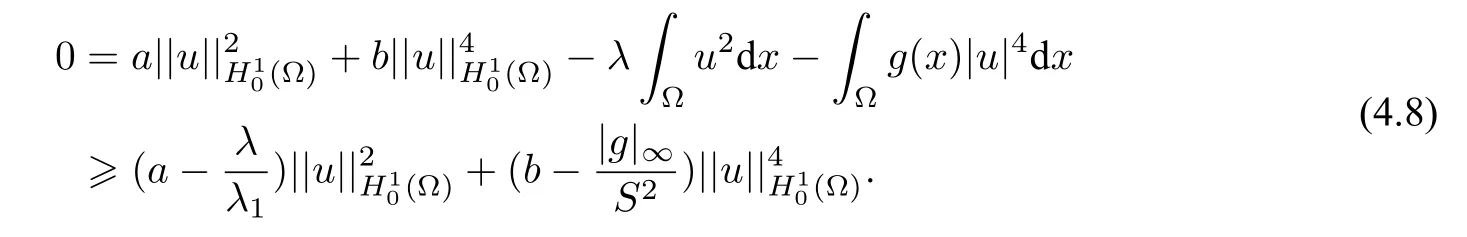

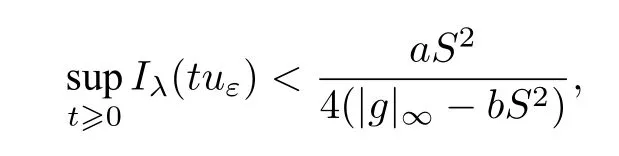
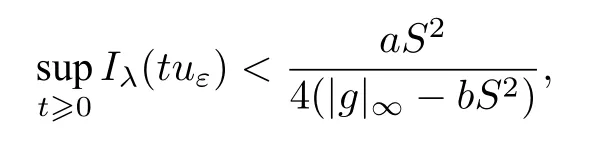
5 Proof of Theorem 1.3