Well-posedness of Time-dependent Nonclassical Diffusion Equation with Memory

Tang Zhipiao Zhang Jiangwei Liu Di

(School of Mathematics and Statistics,Changsha University of Science and Technology,Changsha 410114,China)

Abstract In this paper,we discuss a class of nonclassical diffusion equation with time-dependent damping terms.The existence of global weak solution is obtained by using the nonclassical method of Faedo-Galerkin and analytical techniques.Meanwhile,we also prove the uniqueness of the solution and the continuous dependence on initial value,where the nonlinearity f satisfies arbitrary polynomial growth.

Key words Nonclassical diffusion equation Global weak solution Arbitrary polynomial growth Galerkin’s method

1 Introduction

In this paper,we consider the following initial-boundary value problem for the nonclassical diffusion equation with memory：

where Ω is a bounded smooth domain in Rn(n ≥3),t >τ,τ ∈R is the initial time,the external force termg=g(x)∈H−1(Ω)is known andε(t)∈C1(R)is a decreasing bounded function satisfying that

In the whole paper,unless otherwise stated,z(t)=(u(t),ηt) is the solution of the system(1.13)-(1.14)with initial valuezτ=(uτ,ητ).

As a mathematical and physical model,(1.1) is usually used in the fields of fluid mechanics,solid mechanics,and heat conduction theory[1,2].It mainly considers two aspects:one is the viscosity,the other is the historical influence ofu(such as polymer,high viscosity liquid,etc.[3]).An energy equation is formed to reveal the whole process of diffusion when these two factors are considered,that is,the above evolution equation with memory term(1.1),which is often referred to as a nonclassical diffusion equation.

Ifε(t)=0,then equation(1.1)becomes the usual reaction-diffusion equation with memory,which equation has been researched by many researchers(see e.g.,[4,9]).In addition,for equation (1.1),the current research focuses on the nonclassical diffusion equation with memory whenε(t)=1(see e.g.,[7,8]).Recently,whenk(s)=0,the existence of time-dependent global attractors inHthas been proved by Zhu et al in [9],where the nonlinearityfsatisfies the polynomial growth of arbitraryp −1(p ≥2)order.And in[6],when the nonlinearityfsatisfies the critical exponent growth,the authors have proved the existence of the time-dependent global attractors inHt.

Based on the above analysis,the well-posedness for equation(1.1)will be investigated in this paper,and our conclusion will essentially extend the existing results.

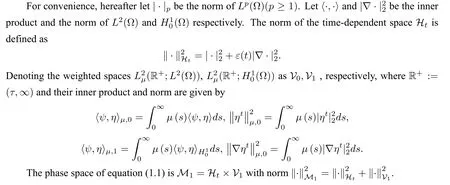
2 Existence of solutions in M1

In this section,we will use the Galerkin approximation method to prove the existence of solutions for equation(1.1).For this purpose,we firstly give the definition of global weak solution as follows.

Definition 2.1For anyT >τ,I=[τ,T],let Ω⊂Rnbe a bounded smooth area,f(u) satisfy(1.6)-(1.7),zτ=(uτ,ητ)∈V1.We say thatz=(u,ηt)is a global weak solution of(1.1),ifzsatisfies(1.13)-(1.14)and

From the theory of ordinary differential equations,(2.2)with initial-boundary condition(2.3)has a unique solution in[τ,T].

In order to obtain the existence theorem 2.1 of solutions,the following some lemmas onzn=(un,)are established.

3 Uniqueness and continuous of solutions

Thus,the uniqueness of solutions and continuous dependence on the initial value for equation (1.1) are proved.This completes the proof.

Acknowledgment

The authors would like to thank the referees for their many helpful comments and suggestions.