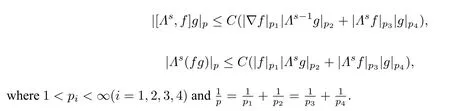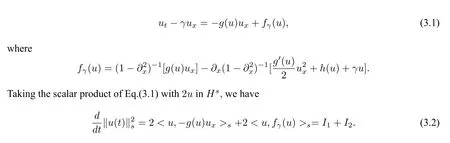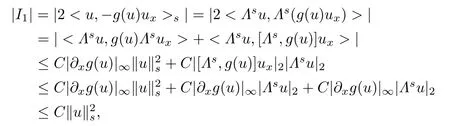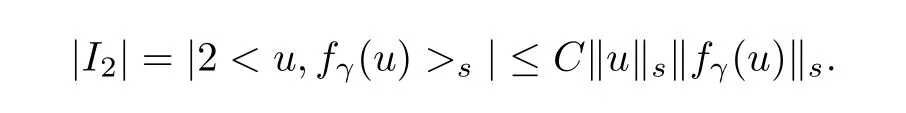Well-posedness and Dispersive Limit Behavior for the Solutions to a Generalized Hyperelastic-rod Wave Equation
Zhang Zaiyun ∗ Liu Zhenhai Zou Pengcheng Wang Qiong Ling Wenjing Ouyang Qiancheng
(1.School of Mathematics,Hunan Institute of Science and Technology,Yueyang 414006,Hunan,China;2.School of Mathematics and Statistics,Yulin Normal University,Yulin 537000,Guangxi,China)
Abstract In this paper,we investigate the local well-posedness and dispersive limit behavior for the solutions to a generalized hyperelastic-rod wave equation(GHR wave equation henceforth)given byBy using Kato’s semigroup approach,we obtain the local well-posedness of GHR wave equation and show that the solution to the equation converges to the solution to the corresponding generalized Camassa-Holm equation as the parameter γ converges to zero.
Key words Generalized hyperelastic-rod wave equation Generalized Camassa-Holm equation Dispersive limit behavior Well-posedness
1 Introduction
In this paper,we investigate the initial value problem(IVP henceforth)associated with a generalized hyperelastic-rod wave equation as follows:
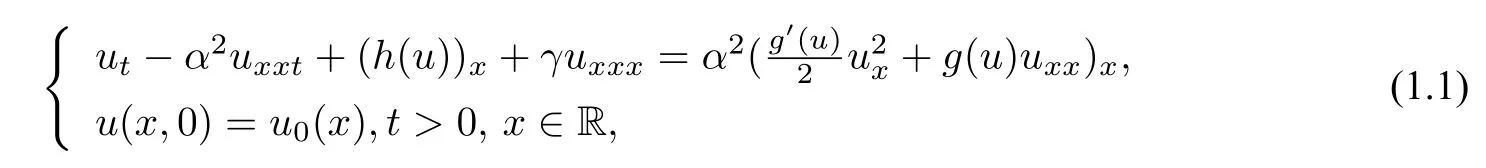
whereh(u),g(u) :R→R are givenC3functions.The solutionurepresents the radial stretch relative to a pre-stressed state.The constantα2is square of length scale and the constantγis given in terms of the material constants and the prestress of the rod.equation(1.1)describing finite length,small amplitude radial deformation waves in cylindrical compressible hyperelastic rods,more details are present in[1-3].
Whenγ=0,(1.1)becomes the HR wave equation or generalized Camassa-Holm equation

Equation (1.2) was first derived by Dai in [2] as a one-dimensional model for finite-length and small-amplitude axial deformation waves in thin cylindrical rods composed of a compressible Mooney-Rivlin material.The derivation relies upon a reductive perturbation technique,and takes into account the nonlinear dispersion of pulses propagating along a rod.It was assumed that each crosssection of the rod is subject to a stretching and rotation in space.There have been many research results with respect to the equation (1.2)[3-15],such as traveling-wave solutions,blow-up of solutions,well-posedness of solutions,the existence of weak solutions,the global solutions of Cauchy problem,the periodic boundary value problem,etc.Among them,Holden and Raynaud [12] studied the following generalized hyperelastic-rod equation:
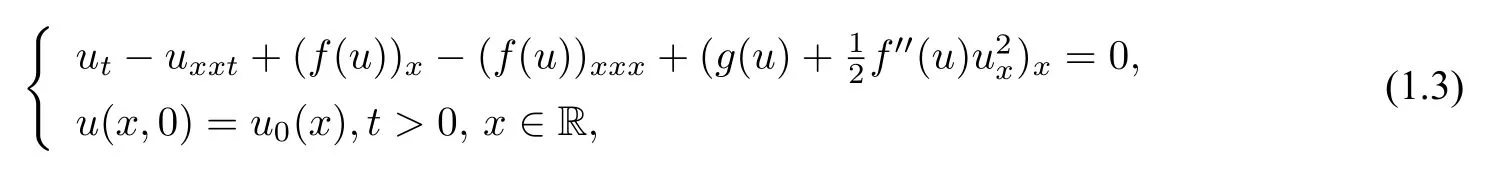
wherefis strictly convex or concave andgis locally uniformly Lipschitz.In fact,(1.3) includes the Camassa-Holm equation(f(u)=andg(u)=ku+u2)as well as the hyperelastic-rod wave equation(f(u)=andg(u)=)as special cases.They considered the Cauchy problem of (1.3) and proved the existence of global and conservative solutions.It is shown that the equation is well-posed for initial datau0∈H1(R),if one includs a Radon measure corresponding to the energy of the system with the initial data.
In particular,forα=1 andg(u)=u,(1.2)becomes

It is worth mentioning that Coclite and his co-workers [9-11] obtained the existence of a global weak solution to(1.4)for any initial functionu0∈H1(R),which extending earlier results for the Camassa-Holm equation by Xin and Zhang,see[16].Moreover,they showed stability of the solution when a regularizing term vanishes based on a vanishing viscosity argument and presented a”weak equals strong”uniqueness result.
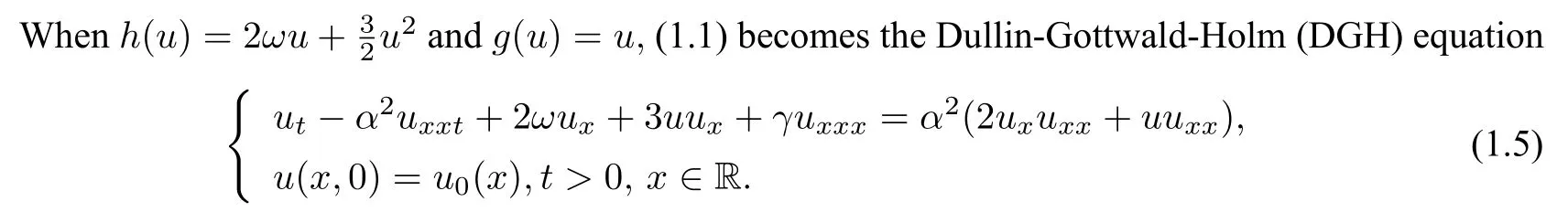
Recently,Tian et al.[17]studied the well-posedness of the Cauchy problem and the scattering problem for the DGH equation(1.5).Also,they investigated that the issue of passing to the limit as the dispersiveγtends to zero for the equation(1.5)and the convergence of solutions to the DGH equation asa2tends to zero.Moreover,they considered the scattering problem with the scattering data and obtained the new exact peaked solitary wave solutions for equation(1.5).Finally,given the condition of existing peak in the DGH equation,they established that it is nonlinearlystable for the peak in equation(1.5).
Based on the above contributions,this paper studies the Cauchy problem and dispersive limit behavior for equation(1.1).That is,benefited from the ideas of[17,18],we investigate the local well-posedness of the GHR wave equation(1.1)and show that the solutions to the above equation converge to the solutions to the corresponding generalized Camassa-Holm equation(1.2)as the parameterγconverges to zero.
The remainder of the paper is organized as follows.In Section 2,we study the local well-posedness of the Cauchy problem(1.1)by Kato’s theory.In section 3,we obtain dispersive limit behavior for equation(1.1)as the parameterγconverges to zero.
NotationsWe will use the standard notation|·|pfor the norm of the spaceLp,1≤p<∞,that is,|u|p=.The spaceL∞=L∞(R)consists of all essentially bounded,Lebesgue measurable functionsuwith the standard norm|u|∞=|u|L∞=|u(x)|.And we denote the norm in the Sobolev spaceHsby
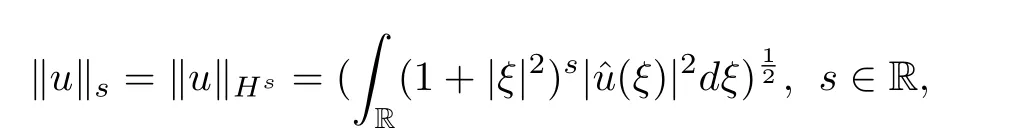
2 Local well-posedness
In this section,we investigate the local well-posedness of the Cauchy problem(1.1)by Kato’s theory.Consider the abstract quasilinear equation

LetXandYbe two real Hilber spaces with norms ∥·∥Xand ∥·∥Y,respectively.Assume thatYis continuously and densely embedded inX.LetQ:Y →Xbe a topological isomorphism.A(u)andfsatisfy the following assumptions:

To facilitate further on our analysis,we next need the following Lemmas.
Lemma 2.1([19])Letrandtbe real numbers such that−r Finally,applying Kato’s theory (i.e.Theorem 2.1) to abstracting quasilinear hyperbolic evolution equation(see[19]),we can obtain the local well-posedness of Eq.(1.1)inHs,for This completes the proof of Theorem 2.2. In this section,we investigate the solutions to (1.1) converge to the solutions to the corresponding generalized Camassa-Holm equation(1.2)as the parameterγconverges to zero. We now present our main results in this section. Theorem 3.1Under the assumption of Theorem 2.2,ifu=uγ1andv=uγ2are the solutions of the Cauchy problem(1.1)inC([0,T);Hs)(s ≥3)withγ=γ1andγ=γ2respectively.Then|u −v|2→0 asγ1,γ2→0. Theorem 3.2Under the assumption of Theorem 2.2,letuγbe the solution of(1.3)inHs,s ≥3.Thenuγconverges to the solution of(1.2)inHs,(s ≥3)asγ →0. Before proceeding to our analysis,we need the following technical lemma. Lemma 3.1([24])LetΛs=.Ifs ≥0,1 Proof of Theorem 3.1The proof is divided into the following two steps. Step 1Firstly,we prove that the solutionuof(1.1)is bounded inHs,s ≥3.Indeed,we can rewrite Eq.(1.1)as Next,we shall estimateI1,I2. Estimate I1It follows from Lemma 3.1 that where in the last estimate we used the result of the uniform boundedness of∂xuin Ref.[17,Lemma 2.5]and the constantCdepends only on the boundMofγ,but notγ. EstimateI2By the Cauchy-Schwarz inequality,we have On the other hand,we have Using the result of the uniform boundedness of∂xuin[17,Lemma 2.5],the differential mean value theorem and the Sobolev embedding,we conclude that Substituting the estimateI1andI2into(3.2),we have whereC=C(|g′(u)|∞,|h′(u)|∞,∥ux∥∞,γ)is independent ofγ,and all|γ|≤M.Applying Gronwall’s inequality,we get that the solutionuof(1.1)is bounded inHs,s ≥3,for anyt ∈[0,T]. Step 2We prove that the sequence of solutions of(1.1)is a Cauchy sequence inL2(R). Letu=uγ1andv=uγ2are the solutions of the Cauchy problem(1.1)withγ=γ1andγ=γ2respectively.Then the functionw=u −vsatisfies the following equation SinceK(∥u∥s∥v∥s)is uniformly bounded and independent ofγ,|w|L2converges to zero asγ1,γ2→0 anduγis a Cauchy sequence inL2asγ →0 uniformly with respect tot ∈[0,T).This completes the proof of Theorem 3.1. Now,we shall prove Theorem 3.2.By Theorem 3.1 and the a priori estimates established for solutions of(1.1)independent ofγ,we can obtain that the Cauchy sequence of solutions of(1.1) locally strongly converges to the solution of(1.2)asγ →0. Proof of Theorem 3.2It follows from Theorem 3.1 thatuγis a Cauchy sequence inL2asγ →0 uniformly with respect tot ∈[0,T).Letu=.Next we show thatuis the solution of(1.2).As a matter of fact,owing touγis the solution of(1.1)inHs,s ≥3,with respect tot ∈[0,T),we have Thus,the RHS of (3.14) is bounded uniformly independent ofγ.Then,using Lebesgue’s dominated convergence theorem and passing to the limit asγ →0 in(3.14),we obtain wheref(u)=f0(u).Therefore,we obtain thatu ∈L∞(0,T;L2)satisfies(1.2).The local existence for the Eq.(1.2)implies that equation(1.2)has a unique solution inC([0,T);Hs),s ≥3.This completes the proof of Theorem 3.2.



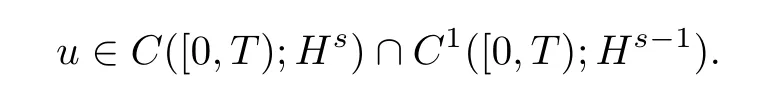
3 Dispersive limit behavior