Distance Integral Graphs Generated by Strong Sum and Strong Product

Lu Junying Liu Weijun Lu Lu

(School of Mathematics and Statistics,Central South University,Changsha 410083,China)

Abstract For two connected graphs G and H,the strong sum G ⊕H is the graph with vertex set V(G)×V(H)and edge set {(u,v)(u′,v′) | uu′ ∈E(G),v= v′} ∪{(u,v)(u′,v′) | uu′ ∈E(G),vv′ ∈E(H)},and the strong product G ⊗H is the graph with vertex set V(G)×V(H)and edge set{(u,v)(u′,v′) | uu′ ∈E(G),v=v′}∪{(u,v)(u′,v′) | uu′ ∈E(G),vv′ ∈E(H)}∪{(u,v)(u′,v′) | u= u′,vv′ ∈E(H)}.In this paper we completely obtain the distances in G ⊕H and G ⊗H when H has diameter less than 3.Furthermore,we get the distance spectra of G⊕H and G⊗H when G and H satisfy some conditions.As applications,some distance integral graphs generated by the strong sum and the strong product are obtained.Especially,we get a new infinite class of distance integral graphs generated by the strong product.

Key words Distance spectrum Distance integral graph Strong sum Strong product

1 Introduction

All graphs considered in this paper are finite,undirected and simple. LetG=(V,E)be a connected graph with vertex setV={v1,v2,...,vn}and edge setE={e1,e2,...,em}. The distance betweenviandvj,denoted bydG(vi,vj)(ord(vi,vj)for short),is defined as the length of a shortest path between them. The diameterd(G)ofGis the largest distance inG,that is,d(G)=. For a vertexvi, denote bythe set of vertices havin g distancekfromvi. It is clear thatV=for anyvi. Note that the setis the neighborhood ofvi, which is also denoted byNG(vi). The distance matrix ofG,denoted byD(G),is then×nmatrix whose(i,j)-entry is equal todG(vi,vj)for 1≤i,j ≤n. SinceD(G) is a real symmetric matrix, all its eigenvalues are real and can be listed asλ1≥λ2≥··· ≥λn. The multiset of such eigenvalues together with their multiplicities is called the distance spectrum ofG,denoted by SpD(G)=whereλ1,...,λsare all the distinct eigenvalues andmiis the multiplicity ofλi. For more details about the distance matrix we refer the readers to[1].

As usual,we always writePn,CnandKnfor the path,the cycle and the complete graph of corresponding orders.For two graphsGandH,the strong sumG ⊕His the graph whose vertex set isV(G)×V(H),and two vertices(u1,w1)and(u2,w2)are adjacent if and only ifu1u2∈E(G)andw1=w2,oru1u2∈E(G)andw1w2∈E(H).Similarly,the strong productG ⊗His the graph whose vertex set isV=V(G)×V(H),vertices(u1,w1)and(u2,w2)being adjacent if and only ifu1=u2andw1w2∈E(H),oru1u2∈E(G)andw1=w2,oru1u2∈E(G)andw1w2∈E(H).A graph is called integral if all eigenvalues of its adjacency matrix are integers.The problem to characterize the integral graphs dates back to 1973 when Harary and Schwenk[2]posed the question“Which graphs have integral spectra ?”.This problem initiated a significant investigation among algebraic graph theorists,trying to construct and classify integral graphs.Although this problem is easy to state,it turns out to be extremely hard.It has been attacked by many mathematicians during the past 40 years [8,9,10,11,12,13],and it is still wide open.With respect to a distance matrix,a connected graphGis called distance integral if all eigenvalues of its distance matrix are integers.Although there is a huge amount of papers that study distance spectrum of graphs and their applications to distance energy of graphs,there are few researches on distance integral graphs.In 2010,Ilić[3]characterized the distance integral circulant graph.In 2011,Renteln[4]characterized the integral Cayley graphs over the Coxeter group.In 2015,Pokorný et al.[5]gave some conditions for the distance integrality on graphs similar to complete split graphs.Very recently,Huang[7]gave some necessary and sufficient conditions for the distance integrity of Cayley graphs over dihedral groups.

In this paper,we derive the distance spectrums ofG ⊕HandG ⊗HwhenGandHare regular with diameters not greater than 2.Particularly,we can remove the restrictions on the graphGwhenH=Kn.From this,we can get a series of distance integral graphs generated by the strong sum and the strong product.

2 Strong sum

In this section we obtain the distance spectrum of the strong sum of two graphs and some distance integral graphs generated by the strong sum.We first prove the following lemma on distance in the strong sum of graphs.

Lemma 2.1LetGandHbe two connected graphs with at least two vertices.Ifd(H)≤2,then for anyu=(u1,w1),v=(u2,w2)∈V(G)×V(H),we have

From Lemma 2.1,we obtain the following conclusion.

Theorem 2.1LetGbe anr1-regular graph with adjacency spectrum{r1,λ2,...,λm}andH,anr2-regular graph with adjacency spectrum{r2,γ2,...,γn}.IfGis triangle-free,d(G)≤2 andd(H)≤2,then the distance spectrum ofG ⊕His

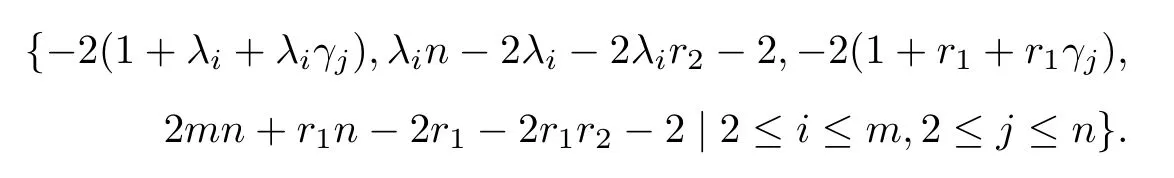
ProofLet the adjacency matrices ofGandHbeA1andA2respectively.From Lemma 2.1,we have

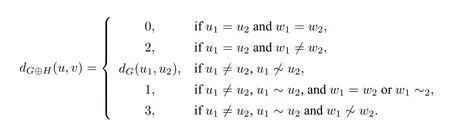
By a suitable ordering of vertices ofG ⊕H,its distance matrixDcan be written in the form

Therefore,−2(1+λi+λiγj),λin−2λi−2λir2−2,−2(1+r1+r1γj)and 2mn+r1n−2r1−2r1r2−2 are eigenvalues ofDwith eigenvectorsxi ⊗yj,xi ⊗jn,jm ⊗yjandjm ⊗jnrespectively.As such eigenvectors are linearly independent,the result follows.

From Theorem 2.1,we get the following result immediately.

Corollary 2.1LetGandHbe two integral regular graphs.IfGis triangle-free,d(G)≤2 andd(H)≤2,thenG ⊕His distance integral.

Similar to Theorem 2.1,we can also obtain the following result from Lemma 2.1.

Theorem 2.2LetGbe anr1-regular graph with adjacency spectrum{r1,λ2,...,λm}andH,anr2-regular graph with adjacency spectrum{r2,γ2,...,γn}.Ifd(H)≤2 andNG(u1)∩NG(u2)for anyu1,u2∈V(G),then the distance spectrum ofG ⊕His

ProofLet the adjacency matrices ofGandHbeA1andA2respectively.From Lemma 2.1,we have

By a suitable ordering of vertices ofG ⊕H,its distance matrixDcan be written in the form

Assume thatjm,x2,...,xmare orthonormal eigenvectors ofA1withA1xi=λixifor 2≤i ≤mandjn,y2,...,ynare orthonormal eigenvectors ofA2withA2yj=γjyjfor 2≤j ≤n.As similar to the proof of Theorem 2.1,we have

Corollary 2.2LetGandHbe two integral regular graphs.Ifd(H)≤2 andNG(u1)∩NG(u2)for anyu1,u2∈V(G),thenG ⊕His distance integral.

By takingG=Kmin Theorem 2.2,the following results are obtained immediately.

Corollary 2.3LetHbe anr-regular graph with adjacency spectrum{r,γ2,...,γn}.Ifd(H)≤2 then the distance spectrum ofKn ⊕His

Corollary 2.4LetHbe an integral regular graph.Ifd(H)≤2 thenKm ⊕His distance integral.

Note that the case will be very different if we takeH=Knin the former results.

Theorem 2.3LetGbe a graph with distance spectrum{µ1,µ2,...,µm}.Then

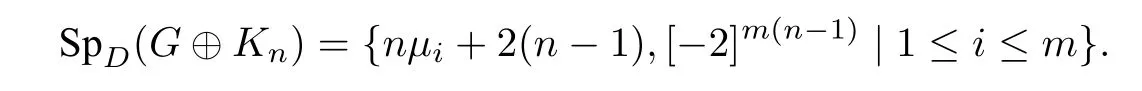
ProofFrom Lemma 2.1,we have

By a suitable ordering of vertices ofG ⊕Kn,its distance matrixDcan be written in the form

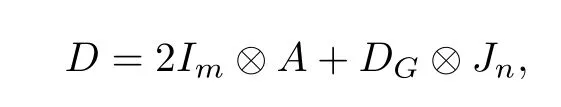
whereAdenotes the adjacency matrix ofKnandDGdenotes the distance matrix ofG.

SinceKnis(n −1)-regular,the all-one column vectorjnof ordern×1 is an eigenvector ofAto the eigenvaluen−1.Let{yj |2≤j ≤n}be the family ofn−1 linearly independent eigenvectors associated with the eigenvalue−1 ofA,thenjnT yj=0 for 2≤j ≤n.Letzibe an eigenvector corresponding to the eigenvalueµiofDG,thenDGzi=µizi.Thus we have

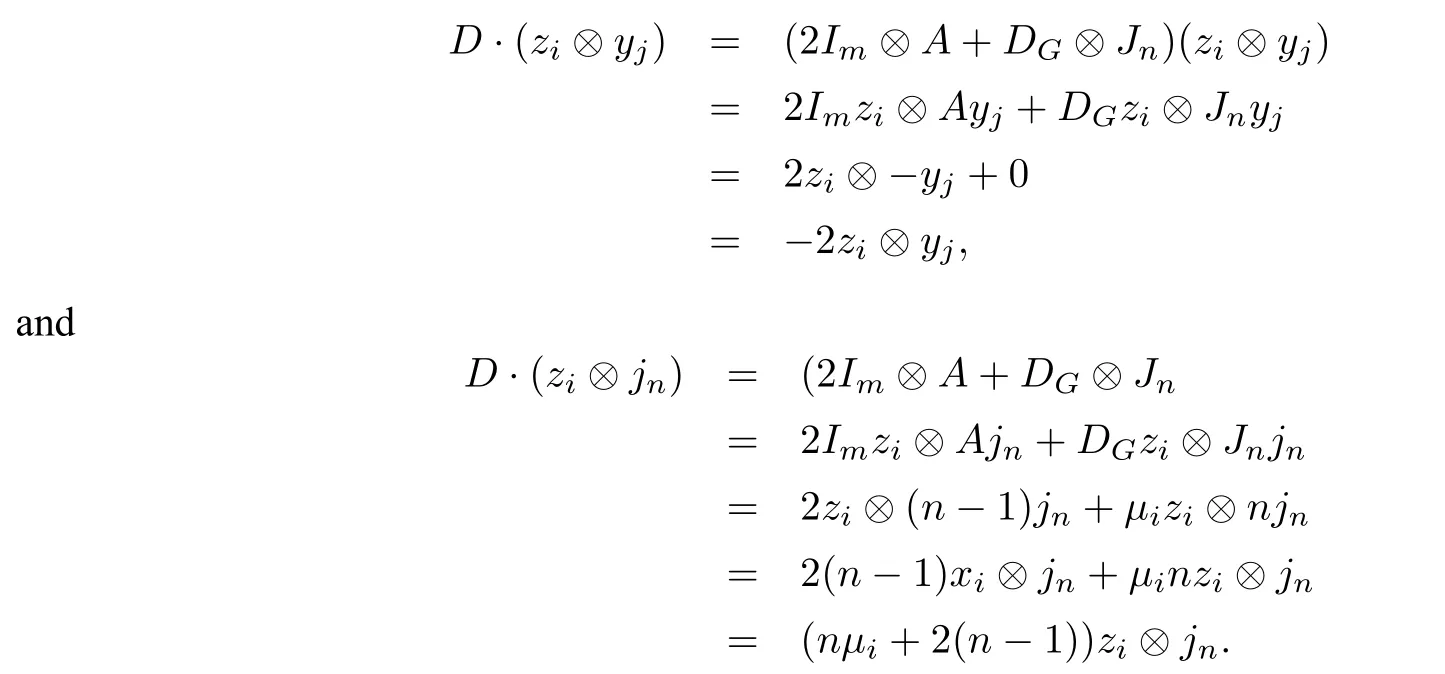
Therefore−2 andnµi+2(n −1) are eigenvalues ofDwith eigenvectorszi ⊗yjandzi ⊗jnrespectively.As the eigenvectors belonging to different eigenvalues are linearly independent,the result follows.

From Theorem 2.3,we get the following corollary immediately.

Corollary 2.5IfGis distance integral,thenG ⊕Knis also distance integral.

Remark 2.1This result has been proved by M.Pokorný et al.[5]by another method.

3 Strong product

In this section we obtain the distance spectrum of the strong product of two graphs and a new class of distance integral graphs generated by the strong product is obtained.We first prove the following lemma on distance in strong product of graphs.

Lemma 3.1LetGandHbe two connected graphs.Ifd(H)≤2 then for anyu=(u1,w1),v=(u2,w2)∈V(G)×V(H),we have

From Lemma 3.1,we obtain the following result.

Theorem 3.1LetGbe anr1-regular graph with adjacency spectrum{r1,λ2,...,λm}andH,anr2-regular graph with adjacency spectrum{r2,γ2,...,γn}.Ifd(G),d(H)≤2,then the distance spectrum ofG ⊗His

ProofLet the adjacency matrices ofGandHbeA1andA2reapectively.From Lemma 3.1,we have

By a suitable ordering of vertices ofG ⊗H,its distance matrixDcan be written in the form

Therefore−2−γj −λi −λiγj,−λi −λir2−r2−2,−2−γj −r1−r1γjand 2mn −r1−r2−r1r2−2 are eigenvalues ofDwith eigenvectorsxi ⊗yj,xi ⊗jn,jm ⊗yjandjm ⊗jnrespectively.As such eigenvectors are linearly independent,the result follows.

Corollary 3.1LetGandHbe two integral regular graphs.Ifd(G),d(H)≤2 thenG ⊗His distance integral.

Note thatG ⊗H=H ⊗G.If one ofGandHis complete,we get the following result.

Theorem 3.2LetGbe a graph with distance spectrum{µ1,µ2,...,µm}.Then the distance spectrum ofG ⊗Knis

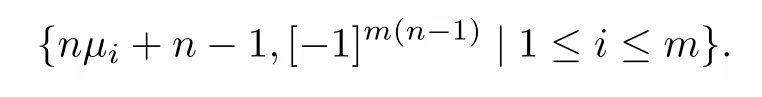
ProofSinced(Kn)=1≤2,we have

from Lemma 3.1.By a suitable ordering of vertices ofG ⊗Kn,its distance matrixDcan be written in the form

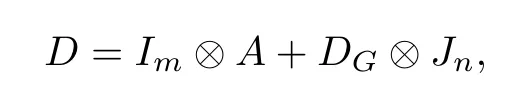
whereAdenotes the adjacency matrix ofKnandDGdenotes the distance matrix ofG.

SinceKnis(n −1)-regular,the all-one column vectorjnof ordern×1 is an eigenvector ofAto the eigenvaluen −1.Let{yj |2≤j ≤n}be the family ofn −1 linearly independent eigenvectors associated with the eigenvalue−1 ofA,then we havejnT yj=0 for 2≤j ≤n.Letzibe an eigenvector corresponding to the eigenvalueµiofDG,then we haveDGzi=µizi.

Now we have

Therefore−1 andnµi+n−1 are eigenvalues ofDwith eigenvectorszi⊗yjandzi⊗jnrespectively.As such eigenvectors are linearly independent,the theorem follows.

Corollary 3.2IfGis distance integral,thenG ⊗Knis also distance integral.

Remark 3.1From Corollary 3.2,we could construct a series of distance integral graphs.For example,the cycleC6is distance integral,thenC6⊗Knis distance integral for any positive integern.