环境噪声驱动下的个体群集动力学研究
翟圣艺 田蓉蓉 程水林
(1.武汉理工大学理学院,武汉,430070;2.中南财经政法大学统计与数学学院,武汉,430073)
1 引言
群集现象源于鸟、鱼、蚁群等生物个体的自组织行为,真菌之间的趋化效应等[1,2,3].在群体内部的个体通过简单的行为规则,彼此之间相互作用,使得整个群体的运动状态保持一致[4,5]的这种行为称为自组织行为.
近年来,自组织行为理论在生物、物理、金融、财务、通信等各个领域广泛应用,然而自组织行为结构错综复杂,却蕴含着丰富的潜在规律与价值,而群集现象是自组织行为的形成机理及作用规律的关键之处,因此迫切需要研究者们更进一步去挖掘群集现象背后的信息和规律,使其可以得到更深入地应用.
1995 年,著名生物学家Vicsek 等[6]首次针对自组织运动形成机制建模,在假定个体以恒定的绝对速度在半径为r的邻域内运动,并考虑随机扰动的情形下,运用数值实验方法验证了该模型会导致从无传输到有传输的动力学相变.
在Vicsek 等人的工作后,相继出现许多的数学模型对群体行为进行研究.其中最主要的是Cucker 和Smale[7]于2007 年提出的著名的Cucker-Smale 模型,运用N个个体相互作用的动力学模型解释大型群体自驱动行为中个体的特性.随着Cucker-Smale 模型在自然科学等领域的广泛运用,涌现出了多种改进的Cucker-Smale 模型.
Ton 等[8]和Luo 等[9]通过分析随机Cucker-Smale 模型,证明该模型全局解的存在性和唯一性,说明了当噪声强度较小时会发生群集现象.Sun 等[10]讨论带有多重噪声的随机Cucker-Smale 模型,通过对其随机稳定性进行分析,发现当噪声强度足够弱且通信速率满足下限条件时,个体会在有限时间以概率1 产生群集现象.Ha 等[11]分析固定噪声强度下的随机Cucker-Smale 模型,得到当通信速率为固定常数时,系统是否发生群集现象与其初始速度及所处位置无关;而当通信速率取决于个体之间的距离时,个体速度围绕平均速度的波动方差具有均匀约束性.Cucker 等[12]研究随机噪声驱动下的Cucker-Smale 模型,结果表明当初始位置和速度满足类似于确定性方程的条件时,系统产生群集效应.Ha 等[13]考虑具有多维白噪声的Cucker-Smale 模型,证明了只要噪声强度足够大,即使通信速率为负值,系统同样会出现群集效应.
然而,对于确定性系统,通信速率为负值时不会出现群集效应,而噪声诱导系统会出现群集效应.受此结果的启发,本文考虑一类特殊环境噪声扰动下的Cucker-Smale 模型.由于随机微分方程显式解中含有随机项,我们考虑去除随机项的影响,以便观察随机微分方程的渐近行为,同时考虑到低阶矩往往比高阶矩更有效,我们采用一种新的估计方法,即估计解的p阶矩(0 在第二节中,我们通过建立两个个体的动力系统模型研究个体之间的群集效应.首先,运用随机微分方程建模,我们得到具有乘性噪声的随机模型在时间趋于无穷时,模型的解一致趋于零,即两个个体之间的速度几乎相等.然后,我们给出不含噪声项的微分方程模型,得到模型的解在时间无限大时处于无穷的状态.结果表明随机模型解的渐近行为能更好地解释个体之间的群集效应. 在第三节中,在假定个体之间相互作用关系相同的情况下,运用最小二乘和极大似然估计方法,对两个个体模型的参数进行估计.通过分析得知:最小二乘法给出的估计量具有无偏性和有效性,而采用极大似然估计方法得到的估计量不具有无偏的性质,但随着样本量n的增大,估计量越来越接近被估总体参数,即具有一致性. 为简单起见,我们考虑由两个个体组成的模型.以X1,t,V1,t分别表示第一个个体在时刻t的位置和速度,X2,t,V2,t分别表示第二个个体在时刻t的位置和速度,模型如下: 其中,x12,v1v2(不妨设v1>v2),ε为任意给定的实数,α,β ∈R,{Wt}t≥0为给定的随机基(Ω,F,P,{Ft}t≥0)上的标准布朗运动. 因为方程(2.1) 的系数满足Lipschitz 条件,所以方程(2.1) 存在唯一的强解[14].令Xt=X1,t −X2,t,Vt=V1,t −V2,t,则系统(2.1)可进一步表示为: 对于这样的两个个体动力系统模型,我们研究当时间t趋于无穷时,两个体之间的群集效应. 定义1称系统(2.2)的解产生群集效应,如果对几乎所有的ω ∈Ω(在后文的公式中,我们用a.s.ω ∈Ω 表示),有 定理1设α,β,ε ∈R,满足 则系统(2.2)会发生群集效应. 在证明定理1 之前,我们给出一个重要的引理. 引理1(重对数率[15]) 设{Wt}t≥0是给定的随机基(Ω,F,P,{Ft}t≥0)上的一维标准布朗运动,则 定理1的证明设对几乎所有的ω ∈Ω,Vt >0.对lnVt应用Itô 公式得: 对上式两边关于时间从0 到t积分得: 于是得到系统(2.2)中两个个体速度差的显式解为: 由式(2.5),∃Ω1⊂Ω,P(Ω1)=1,使当ω ∈Ω1时,∀ε1>0,∃T1(ω)>0,当t>T1(ω)时,有: 于是,对任意的t>T1(ω),我们有 因为−(α+β)−<0,所以当t →+∞,Vt(ω)→0.这样我们就证明了条件(2.3)的第二个式子. 另一方面,对任意的M >1,∃T2(ω)>0,使得当t>T2(ω)时,有: 再将上面估计式代入(2.8)式,得 进而,有 因为θ <0,从不等式(2.9)我们得到群集效应所需的条件(2.3)的第一个式子成立,因此定理1得证. 注1我们还可以计算Vt的p阶矩(p>0). 其中,Wt是一维标准布朗运动.因此 代入式(2.10)即可得到Vt的p阶矩: 其中η=−(α+β)−(1−p). 注2我们也可将确定性系统与随机系统(2.1)进行对比. 在确定性系统中,两个个体满足如下微分方程组: 采用一阶可分离变量的微分方程求解方法,我们得出两个个体的速度差为 进一步,可得 故当α+β <0 时,|Vt|→+∞,|Xt| →+∞(t →+∞),即此时个体不会发生群集;而对于随机模型,由定理1知,只要0>α+β >−,个体即以概率1 发生群集.这表明随机系统和确定性系统有本质性差异:确定性系统在环境噪声扰动后,产生了群集效应. 取模型参数α=β=,并假定v=1.此时,随机模型与确定性模型的两个个体速度差的对比结果如图1 所示.在带有乘性噪声项的随机模型所对应的图1(a)中,的值随时间单调递减,且当时间t趋于无穷时趋于零,并且由定理1,进一步有:两个个体速度之差Vt以概率1 趋于0.而在不带乘性噪声项的确定性模型所对应的图1(b)中,两个个体的速度差Vt随时间单调递增,且在时间t趋于无穷时趋于无穷. 图1 随机模型与确定性模型速度差解的对比 本节讨论两个个体满足的随机模型的参数估计问题. 考虑一种简单情形,假定两个个体相互作用的关系相同,即α与β相等. 由(2.6)式,有 因为Wt是布朗运动,具有独立平稳增量性,故对离散时间点1,我们有:Ui与Uj相互独立,且Ui ∼N(0,1),即序列{Ui}1≤i≤n为白噪声正态序列,记为Ui ∼WN(0,1). 利用{Ui}1≤i≤n,我们有 因此,得到似然函数 取对数,得到对数似然函数 再关于λ求偏导得: 令(3.4)式等于零,解得: 再将对数似然函数关于ε2求偏导并令其等于0,得: 由此,得到参数α,β的估计值为: 容易算得 所以,α,ε2的极大似然估计都是渐近无偏的. 本文研究带有乘性环境噪声的Cucker-Smale 模型,讨论了不同模型参数和噪声强度对模型解的渐近行为的影响,发现存在适当的噪声强度,导致系统以概率1 出现群集效应.但对于不带有环境噪声的确定性系统,个体间的群集效应并未产生.这说明乘性白噪声的引入会导致个体群集效应的产生.2 模型的建立与求解
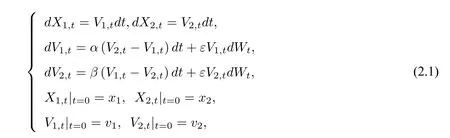

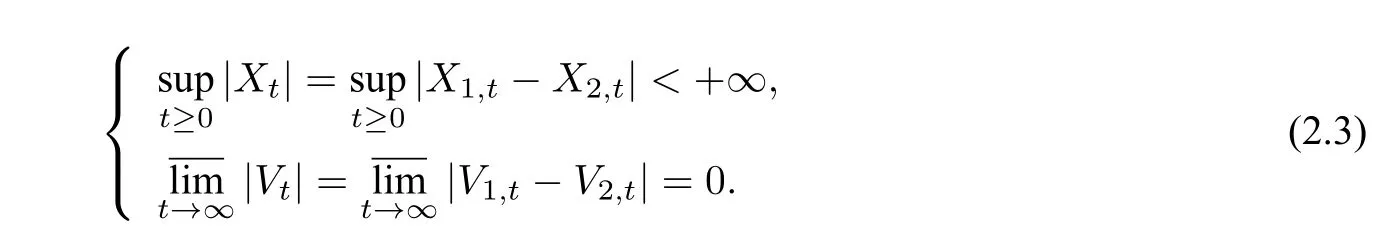


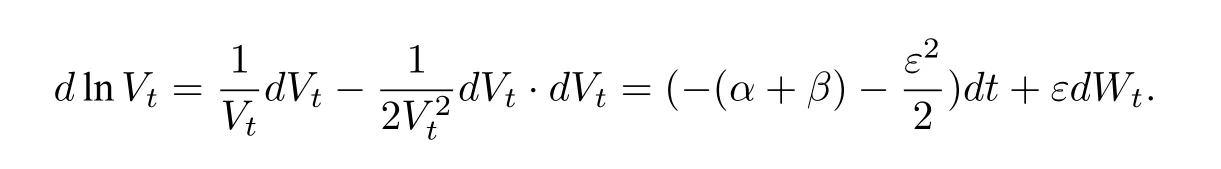
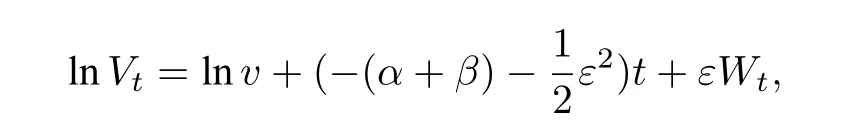
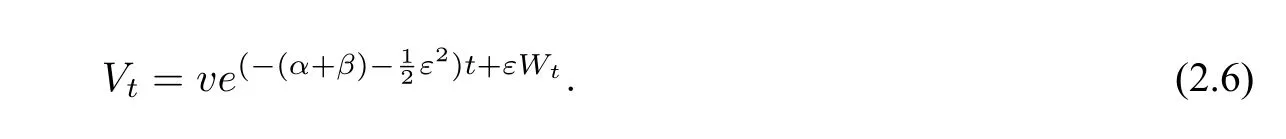
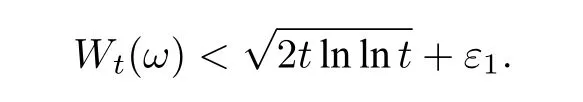
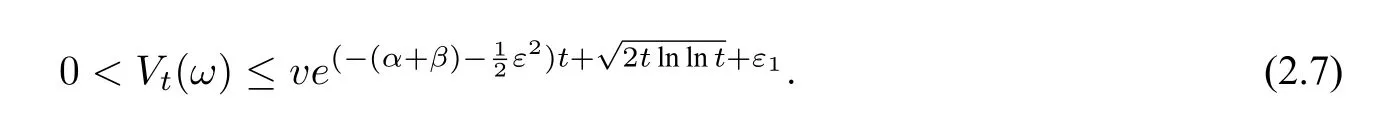

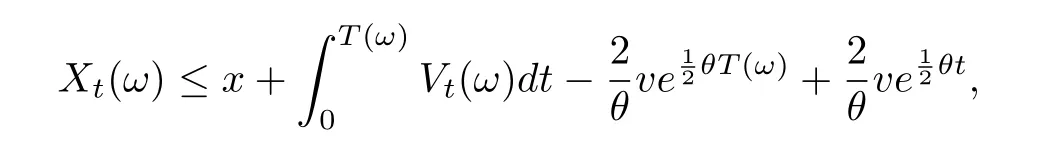
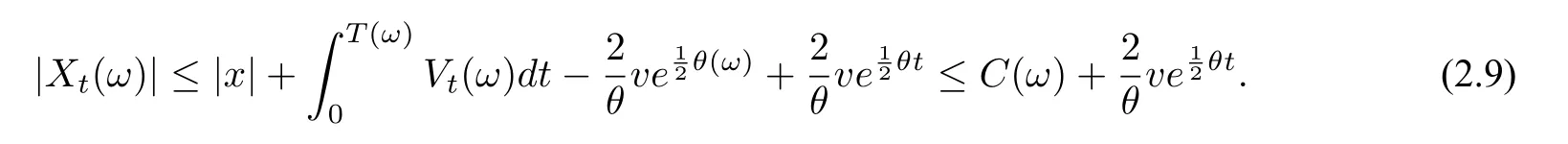
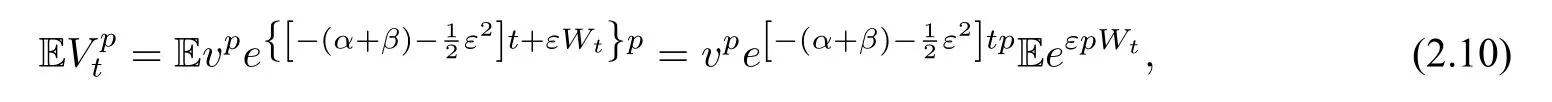

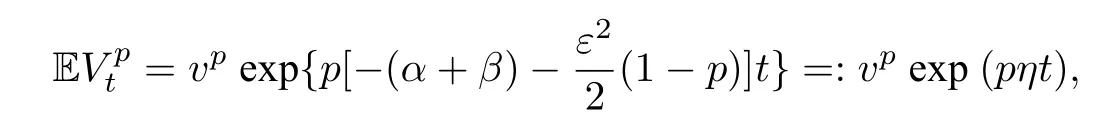
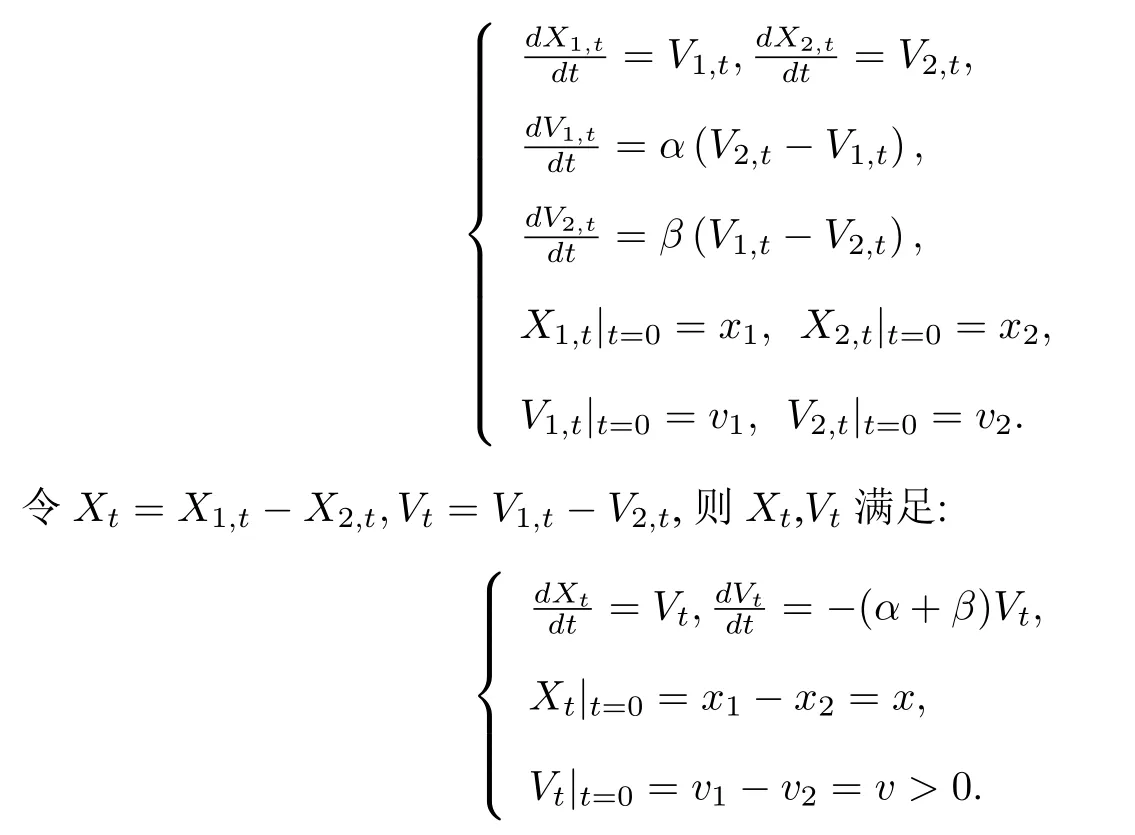
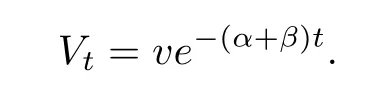
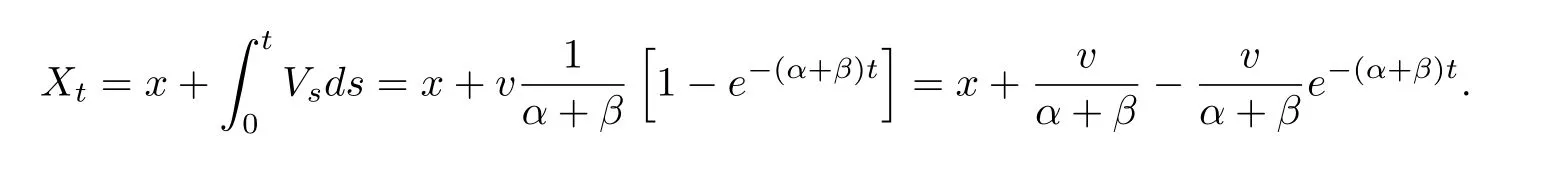
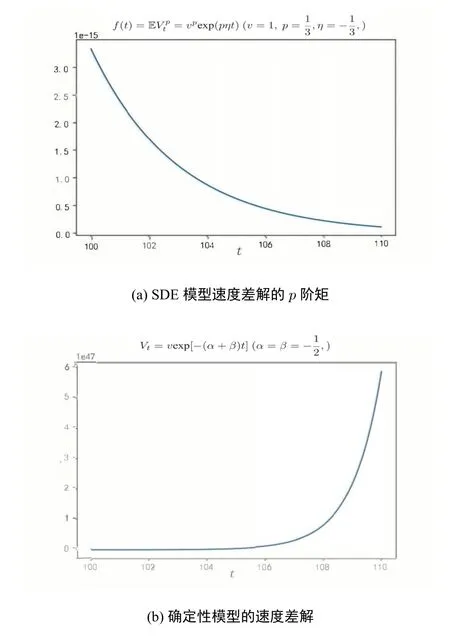
3 模型的参数估计


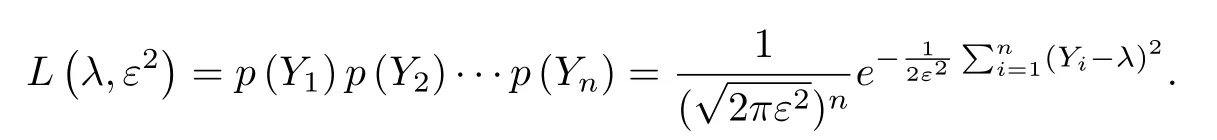
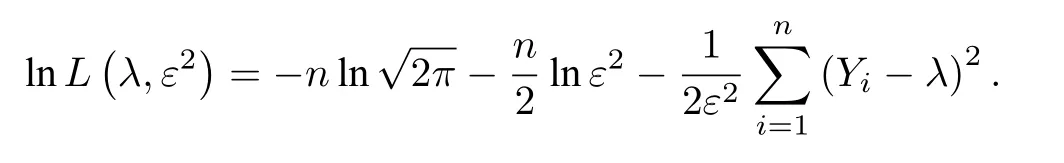

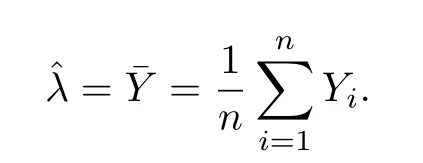


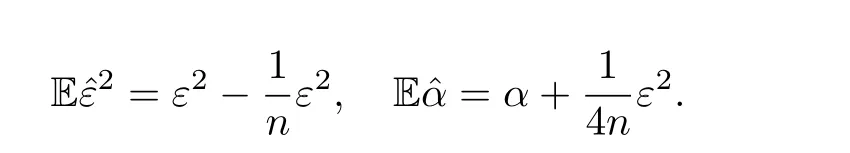
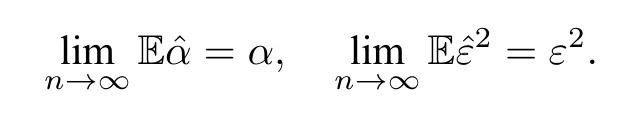
4 结论
- 数学理论与应用的其它文章
- 一类具有非线性扰动的新冠肺炎SIRC 随机模型研究
- Further Discussion for Generalized Normal Sectors in Class II
- Distance Integral Graphs Generated by Strong Sum and Strong Product
- Well-posedness and Dispersive Limit Behavior for the Solutions to a Generalized Hyperelastic-rod Wave Equation
- An Improved Image Fusion Method Based on a Wavelet Transform
- Existence of Positive Solutions for a Critical Kirchhoff Type Equation with a Sign Changing Potential

