讲授Bishop条分法时引入新研究成果的探索

雷 胜 友

(长安大学 公路学院， 陕西 西安 710064)

土力学是土木工程专业大学生的专业基础课，如何结合课堂讲授，启发大学生的创新思维，为达此目的，笔者尝试着将自己的一些研究成果揉进课程的讲授中，以推动大学生的创新思维。在目前我国流行的土力学教材上，Bishop法土坡稳定分析是其重要的一节，属必讲内容，笔者在讲授这部分内容时，经过反复思考[1-11]，结合土的强度表达式中各参数的特点，觉得库仑强度折减式可以做一改进，将其运用到土坡稳定分析中，进一步可以改进Bishop法土坡稳定安全系数表达式，如果把这些研究成果引入课堂教学，可以大大地激发学生们的好奇心，启发他们深入思考，触动他们发散思维，培养他们对科学研究的兴趣。

1 新强度折减式的构思

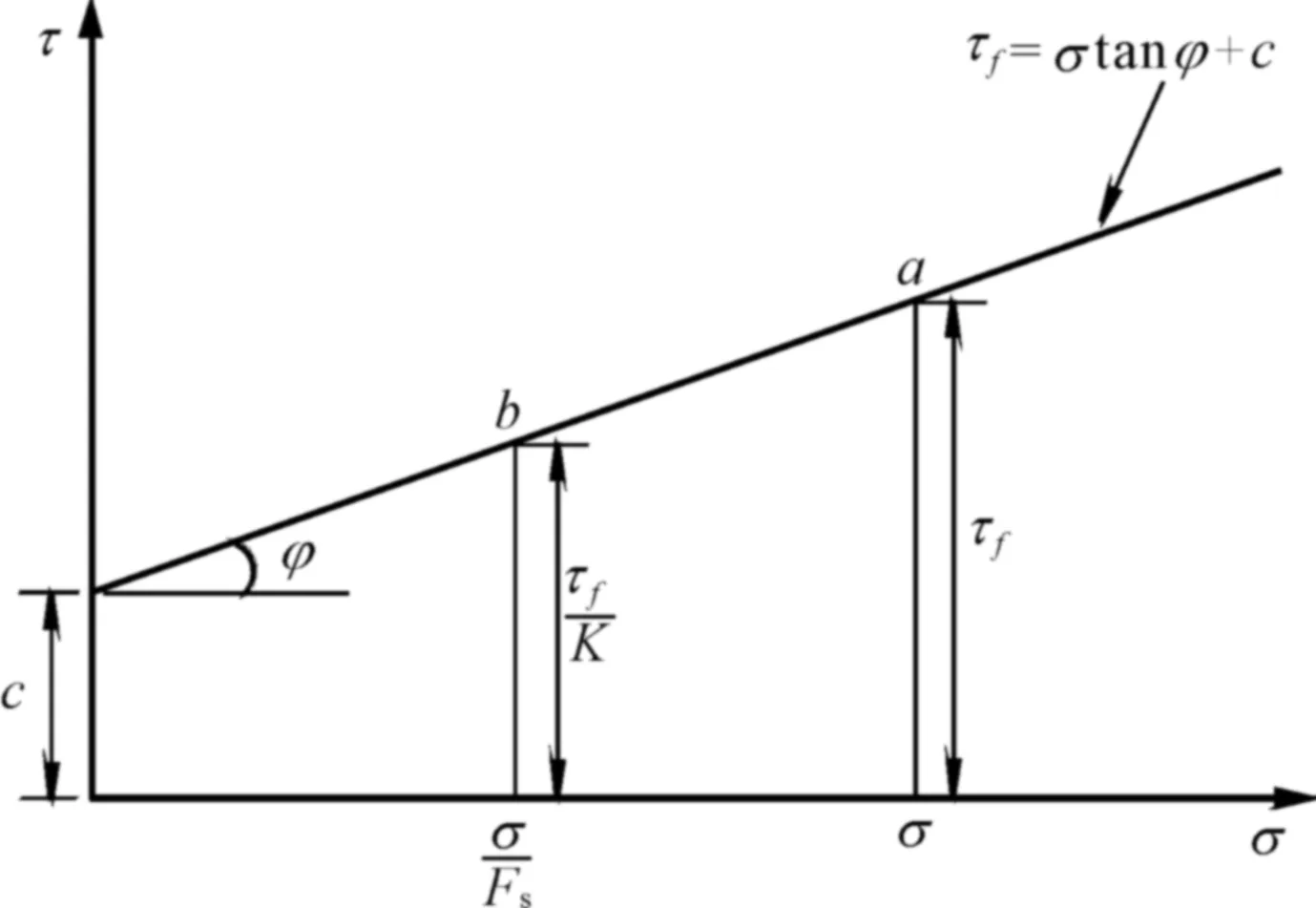
图1 a点、b点剪切强度

2 改进后的Bishop土坡稳定安全系数表达式

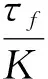
(1)

简写为：

(2)

3 用改进的Bishop法进行土坡稳定分析

为了进一步验证改进的Bishop法土坡安全系数表达式的合理性，笔者在讲授本科生土力学时，从我校图书馆搜寻目前流行的土力学教材，经过梳理、分类，共有17道土坡稳定分析的例题[12-28]，每道例题都用改进的土坡安全系数表达式进行计算，同时又对现有的17道例题的计算结果进行检查、复核，发现个别例题结果有误，并进行纠正。现将两种方法所得土坡安全系数放在一起,以作比较，结果如图2所示。

图2 本文结果与Bishop法比较

从图2可知，使用式(1)计算的土坡稳定安全系数均比简化Bishop法小，其小的百分比为0.23%～23.35%，其中，百分比在5%以内的有8例,大于5%的有9例,大于10%的有5例,大于15%的有2例,大于23%的有1例。由此可见，对于工程而言，用式(1)计算的安全系数偏于安全。

4 授课环节的实施

在讲课之前，笔者先将改进后的土坡安全系数表达式的相关内容通过互联网，发到授课班级群，让学生们下载、阅读，并线上指导学生理解强度折减表达式的构思过程，同时让学生进一步熟悉Bishop条分法的基本思想，为随后的课堂听讲做知识铺垫和准备。在课堂授课中，笔者对比分析改进的强度折减式与通常的强度折减式的不同之处，说明改进的强度折减式的合理之处，然后将改进的强度折减式代入Bishop法土坡稳定系数表达式内，通过化简得到改进的Bishop法土坡稳定安全系数表达式，随后检查改进后的Bishop法土坡安全系数表达式中的各项，说明如何实施编程、迭代计算。在授课结束后，给学生布置一道作业题，让学生试着用改进的Bishop法土坡稳定系数表达式计算粘性土坡的安全系数。

5 课后回访与思考

本次授课对象为我校桥梁与渡河工程专业的本科生，授课班上共有学生35人，桥梁与渡河工程专业为我校重点学科，该班学生基础较好，后来又转入新工科试验班学生3人。通过课后与学生的交谈，发现学生对于土的强度认识又进了一步，对于土的强度参数的意义理解得比较清楚了，好多学生对于书本内容不再盲从了，纷纷提出了自己的看法，有些想法尽管不成熟，但毕竟启发了学生的独立思考。另外，通过本次讲授，也启发了笔者，可否将强度折减的概念先放在本课程的土的强度一节进行介绍，以引起学生们的兴趣，让学生先有个知识铺垫，然后再在土坡稳定部分展开详细推导，进而发动学生用两种土坡安全系数表达式进行土坡稳定分析，想必这样的教学效果会更好些，笔者打算在下个学期的土力学讲授中做一尝试。

反观本文强度折减式的构思以及土坡稳定安全系数的推导,实际上暗含了这样的假定:即滑动面上的黏聚力首先得到发挥，然后不足部分由摩阻力来补充,这一研究思路与土坡稳定分析中的摩擦圆法的思路正好相反，相比较而言，本文的思路更合理些。

实质上,本文所得土坡稳定安全系数是对摩阻力而言的，对黏聚力的安全系数为1。

根据有关资料的介绍[13]，Bishop法所得土坡稳定安全系数大于瑞典条分法，那么改进的Bishop法所得土坡安全系数是否也大于瑞典条法？为此，笔者将瑞典条分法所得安全系数与式(1)结果做一比较，如图3所示，从图中可知，有6道例题用式(2)所得安全系数均比瑞典条分法小，其小的百分比为0.74%～16.26%，其中只有1例的百分比大于10%；其余11道例题用式(2)计算所得安全系数均大于瑞典条分法，大的百分比为0.83%～34.79%，进一步分析可知，百分比在5%以内的有4例，大于5%的有7例，大于10%的有3例，大于20%的有2例，大于30%的有1例。综合以上结果可知，两者安全系数相差百分比在10%以内的共有13例，而大于10%的有4例，仅占总数的23.5%。

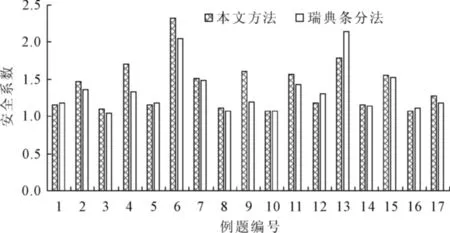
图3 本文结果与瑞典条分法的比较

综合分析，改进的Bishop法土坡安全系数表达式可用于实际的土坡稳定分析。

追根溯源，由表达式τf=σtanφ+c可知,土的强度由黏聚力和摩阻力两部分组成，当法向应力σ=0或者φ=0时，τf=c；当σ≠0或者φ≠0时，才有τf=σtanφ+c的形式。在极限平衡状态时，当剪切力大于粘聚力，即τf>c时，也是黏聚力首先得到充分发挥，然后剩余部分的剪应力则由摩阻力来平衡，即总的可写成τf=σtanφ+c；τf

当土为饱和状态时，φ=0，则土坡的安全系数为：

(3)

当c=0时，即为砂性土，土坡的安全系数可否按下式进行迭代计算：

(4)

当αi=α，φi=φ时，上式可简化为

(5)

6 结 语

将最新的研究成果引入到本科生的教学中来，可以有效地传播新知识，进一步拓展课本内容，引起学生的发散思维，激发他们对科学研究的兴趣，达到教书育人的目的。