土钉加固黏性土坡加载的离心模型试验研究

曹 洁，张 嘎，王丽萍

（清华大学 水沙科学与水利水电工程国家重点实验室，北京 100084）

1 引 言

工程中很多浅基础都修建在土质边坡上，包括堤防上的建筑，山坡上的公路、桥台和房屋等。岩土工程实例表明[1－2]，建筑浅基础在边坡坡顶施加的荷载将严重影响边坡的稳定性，从而导致滑坡灾害的频发。为了提高坡顶加载情况下土质边坡的稳定性，减轻滑坡灾害，工程中采用了各种加固方式。土钉作为一种原位加筋技术，因其施工工艺简单，经济效益显著等优点被应用到各种加固工程中，尤其是在高边坡和深基坑等工程中土钉加固技术发展迅速[3－6]。

随着对边坡加固方式研究的深入，坡顶加载条件下加固土坡的研究逐渐成为岩土工程一个重要的课题[1－2，7－8]。例如，Bathurst 和陶连金[2]进行了大型室内试验，研究了土工格栅加固和未加固边坡在坡顶荷载作用下的变形与破坏规律。Sawwaf 采用模型试验和数值模拟两种方法对坡顶加载条件下抗滑桩加固砂土边坡的变形和承载特性进行了研究，考虑了抗滑桩长度、位置、粗糙程度等多种影响因素。

离心模型试验可以再现自重应力场以及与自重有关的变形过程，在加固土坡的相关研究中得到了较广泛的应用[9－10]。但在对边坡承受坡顶加载工况的研究中较少采用离心模型试验手段，针对以土钉为加固方式的黏性土坡的研究则更少。因此，有必要对加固土坡承载和变形规律开展研究，为揭示坡顶加载工况下加固土坡的破坏机制奠定基础。

本文采用离心模型试验方法，在土钉加固黏性土坡坡顶施加竖向荷载，再现了土坡的变形破坏过程。测量了土钉加固土坡在加载过程中的位移场变化，分析了土坡的变形破坏规律以及土钉的变形规律。初步探讨了土钉与土之间的相互作用特性和坡角对土坡承载变形的影响。

2 试验设备和测量技术

2.1 设备

本试验在清华大学50 g∙t 的土工离心机上进行，该离心机的有效半径2 m，可提供的最大离心加速度为250 g。

试验采用离心场坡表加载设备对边坡施加坡顶荷载，加载速率为2.5 mm/s，加载底板宽6.5 cm，长20 cm，用来模拟坡顶的浅基础，上下两块加载底板之间配置有滚动轴承，使下底板在加载过程中与坡表一起移动。

试验使用的铝合金模型箱，尺寸为50 cm× 20 cm×35 cm，一侧为透明的有机厚玻璃板，便于在试验过程中观察模型土坡的变形。

2.2 测量系统

试验中采用离心场高质量图像采集与非接触位移测量系统来记录和测量土坡的位移场[11]。数据分析的具体步骤为[12]：（1）将白色水磨石颗粒嵌入土坡模型侧面以形成位移测量需要的具有随机性分布的较大色彩差的测量区域；（2）由固定在模型箱上的摄像头透过有机玻璃记录边坡在加载过程中的形态；（3）将录像拆分成数字照片系列；（4）根据测量需要确定测点网格；（5）基于相关分析理论和算法来确定任意时刻土体表面任意一点的位移，精度达0.03 mm。

加载过程中，采用荷载传感器测量坡顶荷载，其可测量的最大荷载值为10 kN。采用激光传感器测量土坡坡顶的沉降量，其测量精度可达0.1%，量程为40～160 mm。荷载传感器和激光传感器均与离心机的数据采集系统相连接，可以实现坡顶荷载和沉降的实时记录。

3 试验模型和试验过程

3.1 试验模型

试验所用的模型箱有机玻璃内侧涂有硅油，相对的另一个侧面涂有硅油并贴上聚四氟乙烯薄膜，从而减小模型箱侧壁与土体间的摩擦。

试验所用黏性土的液限为33.7，塑限为15.5，土坡模型的击实干密度控制为1.51 g/cm3，含水率为17.0%。制样时，先分层击实至所需干密度，然后削去多余土样形成土坡，并在土坡底部保留5 cm厚的水平土层，以减小土坡与模型箱底板间的摩擦。

考虑到偏危险的情形，以及对现场实际情况进行的适当简化，试验中采用圆截面钢丝来模拟土钉，钢丝的弹性模量为210 GPa，直径为1 mm，表面未进行特别处理。根据离心模型试验的比尺，当离心加速度达到50 g 时，模型中的铁丝相当于原型直径为5 cm 的土钉。土钉沿垂直于边坡方向插入土坡10 cm，间隔2.5 cm 布置。

本文进行了3 种坡角条件下土钉加固黏性土坡的离心模型试验，分别为2：1、3：1 和5：1（竖直：水平），其中3：1 土坡的模型布置如图1 所示。建立图中所示的平面直角坐标系，以加载底板中线与坡顶表面的交点为原点，规定水平方向以向右为正，竖向方向以向下为正。

图1 3:1 土坡模型示意图 (单位：cm) Fig.1 Schematic drawing of 3:1 slope model (unit: cm)

3.2 试验过程

试验开始后，首先进行静力加载过程。每一级离心加速度增量为5 g，待土坡变形稳定约2 min 后进行下一级加载，当离心加速度达到50 g 且变形稳定之后即启动坡顶加载设备开始坡顶加载。与此同时，荷载传感器和激光传感器与数据采集系统相连进行数据采集，图像采集系统以10 帧/s 的帧率采集图像。本文的试验结果是按照模型尺寸给出，可以根据离心模型试验比尺关系换算到原型。

4 试验结果

4.1 边坡承载力和变形

图2 给出了加载过程中，坡顶荷载P 与坡顶沉降S 之间的关系曲线。可以看出，对于不同坡角加固土坡的P-S 曲线，坡角越大曲线越平缓。边坡的承载能力随着坡角的增大逐渐降低。

图2 坡顶竖向荷载P 与坡顶沉降S 间的关系曲线 Fig.2 Relationships between vertical load and slope top settlement

图3 加载过程中土坡位移场 Fig.3 Displacement fields of slopes during loading

2：1 加固土坡在坡顶发生不同沉降时的位移等 值线如图3 的(b)、(c)和(d)所示，其中进行位移测量和分析的区域范围为图1 中所示虚线内区域。在相同坡顶沉降下，土体的水平位移从土坡的内部向表面逐渐增大，最大值出现在土坡表面的中上部；竖向位移由土坡的顶部向底部逐渐减小，坡顶加载底板作用位置处数值最大。随着坡顶沉降的增加，土体的位移逐渐增大，土坡内部的变形集中区域形成并逐渐发展。

图3(a)给出了坡顶沉降S =1 cm时3：1 加固土坡的位移场，此时坡顶荷载为48 kPa，比2：1 加固边坡在S =1 cm 时的荷载小很多，且此时土坡内部和坡面附近位置均出现了明显的变形集中，与图4 所示的照片中土坡滑裂面的形成相对应。2：1 和3：1 加固土坡位移场的对比说明，坡度越大的土坡在较低的坡顶荷载水平下将产生越大的变形，滑动破坏越容易发生。

图4 3:1 加固土坡坡顶沉降1 cm 时的照片 Fig. 4 Image of 3:1 reinforced slope at slope top settlement of 1 cm

4.2 边坡破坏过程

基于3：1 加固土坡水平位移场的分析结果，进一步分析土坡在坡顶荷载作用下的破坏过程。沿图4 中所示的土坡滑裂面选取了几个区域的部分测点（如图5 中的T1～T25），分析了它们的水平位移u在加载过程中的变化情况。同一位置处选取了5 个连续的测点，相邻两点的水平间距约为4 mm。图6给出了T1～T10测点的水平位移在加载过程中的时程曲线。可以看出，在加载初期（P =10 kPa），土坡的坡顶处相邻测点T3 和T4 之间发生较大的相对位移，并随着坡顶荷载的增大逐渐趋于稳定，而其余测点之间并没有发生显著的相对位移，边坡的滑裂面可能在T3 和T4 测点之间发生。当坡顶荷载P=20 kPa 时，土坡中部相邻测点T8 和T9 之间开始产生较大的相对位移，但相对变形小于前者，可推断其出现是坡顶变形集中发展的结果。

图5 土坡变形集中区域测点位置示意图 Fig.5 Locations of measured points near slip surfaces

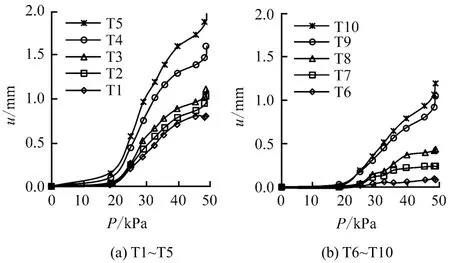
图6 土坡内部测点的位移变化 Fig.6 Displacement histories of internal measured points of slope

图7 土坡坡面附近测点的位移变化 Fig.7 Displacement histories of measured points near slope surface

坡面附近的T11～T25 测点的水平位移在加载过程中的时程曲线如图7所示，坡面中下部测点T23和T24 最先开始发生较大的相对位移。当P =35，40 kPa 时，坡面中部以及边坡上部测点之间开始出现相对位移，但与坡面中下部测点间的相对位移相比不明显，这与土坡中上部的土体在坡顶荷载作用下发生显著竖向压缩变形有关。

从以上的分析可以判断，加载过程中，测点间较大的相对位移的出现表征了土坡内部的变形集中，变形集中区域的发展连通导致了滑裂面的形成。根据不同区域各组测点发生较大相对位移的位置，将土坡的滑裂面标识在图8 中，并给出了各处测点发生变形集中时的坡顶荷载。可以看出，土坡内部的深层滑裂面在加载初期产生于坡顶加载底板左边缘区域（T1～T5），并随着坡顶荷载的增加向土坡中部（T6～T10）发展，坡顶荷载达到20 kPa 之后逐渐趋于稳定，这主要与加载底板的竖向运动及土钉的加固作用有关。土坡坡面附近的滑裂面产生于坡面中下部区域，并不断向坡顶方向扩展，在坡顶荷载约35 kPa 时经过T16～T20 区域，约40 kPa 时发展至接近坡顶的T11～T15 区域，最终导致土坡发生了坡面附近的滑裂破坏。

图8 土坡的破坏过程 Fig.8 Failure process of slope

5 加固土坡变形规律分析

5.1 坡顶加载对加固土坡变形规律的影响

为了进一步分析坡顶加载对土坡变形的影响，在土坡若干高程处沿水平线取了一系列点，研究不同高程处土体的竖向位移分布。图9 给出了3：1 加固土坡4 个高程位置（自上而下y =3，9，15、21 cm）在坡顶沉降分别为0.5、1 cm 时的竖向位移分布，以及2：1 加固土坡在坡顶沉降为1 cm时的竖向位移分布。图中的两条虚线表示加载底板的左、右边缘延长线，竖向位移用v 表示。

对于3：1 加固土坡，土体的竖向位移随着坡顶沉降的增加而不断增大。当坡顶沉降一定时，土体竖向位移分布随着高程不同而发生变化。土体离坡顶越远，竖向位移的最大值越小，竖向位移的分布曲线在加载底板宽度范围内越趋于平缓。

图9 土坡不同高程的竖向位移分布 Fig.9 Distributions of vertical displacements of slope at different heights

S =1 cm 时，2：1 的加固土坡竖向位移分布与3：1的土坡相比，两者存在较大差异。对于2：1 的加固土坡，在y =3 cm 和y =9 cm 两个高程，土体竖向位移的分布曲线在加载底板宽度范围内呈现显著的“尖峰”状，竖向位移的最大值近似对应于加载底板 的中线位置，而在y =15 cm 和y =21 cm 两个高程，竖向位移自坡内侧向外逐渐增大，最大值并未出现在加载底板的宽度范围内；对于3：1 的加固土坡，边坡上部的土体竖向位移在加载底板宽度范围内并没有呈现如2：1 土坡那样明显的“尖峰”状分布，而在边坡中部两个高程处，分布曲线在加载底板右边缘右侧存在明显的位移拐点，该拐点外侧各点的竖向位移表现出较快的增大趋势，这主要是因为3：1土坡的坡面滑裂面经过了上述两个高程位置，相邻测点间发生了较大的相对位移。

从土坡竖向位移最大值的分布可以看出，土坡最大竖向位移的位置从土坡坡顶向坡底部逐渐移出加载底板的宽度范围。这表明，加载底板对土坡竖向变形的影响是随着高程的降低而逐渐减弱的。通过两种坡度加固土坡的对比又可以看出，当坡顶沉降相同时，3：1 土坡最大竖向位移出现的位置移出加载底板宽度范围时的高程要明显大于2：1 土坡，并且土体最大竖向位移的位置更靠近边坡表面。这表明在坡顶竖向荷载作用下，随着坡度的增大，土体向坡面变形的趋势更为显著。

5.2 土钉的变形规律

在土钉加固土坡中，土钉与土体形成复合体，时刻与土体相互影响、共同作用[7]。当土坡承受坡顶竖向荷载时，土与土钉在垂直于土钉方向上不会发生脱离，土钉对土体的变形产生约束，并与土体一同承担荷载。据此，土钉沿垂直于土钉方向的变形，即土钉的挠度，可以近似通过测量土钉周围土体的变形得到，进而得到土钉形态的空间分布规律和在加载过程中的变化情况，这满足土钉与其周围土体变形协调的要求。

在土坡内部上、中、下3 个区域沿钉长方向选取了一系列测点，由它们的水平位移和竖向位移求得相应区域土钉的挠度r，建立图10 中所示的直角坐标系XOY。图10 给出了3：1 土坡内的土钉在加载过程中的形态变化情况。可以看出，同一区域处（如图10（c）中的P1），土钉的挠度随着坡顶沉降的增大而增大；坡顶沉降一定时，不同区域土钉的形态不同，土钉与坡顶距离越远，挠度分布曲线越平缓，变形越小；同时由于土体在加载过程中向坡面移动，使得土钉的变形从土坡内部向土坡表面整体上呈现增大的趋势。可以推断，钉土间的相互作用随着坡顶荷载的增大逐渐增强，且在土坡内部的不同区域呈现出不同的特征。

图10 3:1 土坡在加载过程中内部土钉的挠度分布 Fig.10 Distributions of nail deflection at different regions of the 3:1 reinforced slope

6 结 论

（1）土坡的水平位移和竖向位移随着坡顶荷载的增加而逐渐变大；加载过程中土坡内部以及坡面附近均发生了变形集中，深层的滑裂面由加载底板左边缘向土坡中部发展并在最后趋于稳定，坡面中、下部的变形集中逐渐向坡顶发展并形成贯通的破坏面。

（2）加载底板对土体的压缩作用从坡顶向坡底部逐渐减弱。

（3）土钉的变形特征因加载阶段和土钉在土坡内的位置不同而不同，坡顶荷载越大，越靠近坡顶的土钉弯曲挠度越大，钉-土间的相互作用越强烈。

（4）土坡的坡角对加固土坡的承载特性和破坏规律有一定的影响。加固土坡坡度越大，边坡的承载力越低；在较低的坡顶荷载水平下滑动破坏越容易发生；土坡最大竖向位移出现的位置移出加载底板宽度范围时的高程越大，土体向坡面位移的趋势越显著。

[1] ALAMSHAHI S， HATAF N. Bearing capacity of strip footings on sand slopes reinforced with geogrid and grid-anchor[J]. Geotextiles and Geomembranes， 2009， 27： 217－226.

[2] BATHURST R， 陶连金. 加筋边坡在坡顶荷载作用下的极限承载能力[J]. 岩土工程学报， 2004， 26(2)： 194－197. BATHURST R， TAO Lian-jin. Study on ultimate bearing capacity of reinforced slopes with full-scale model test[J]. Chinese Journal of Geotechnical Engineering， 2004， 26(2)： 194－197.

[3] 王军. 土钉墙在边坡加固中的应用[J]. 岩土工程界， 2008， 11(11)： 50－52. WANG Jun. Application of soil nailing wall to slope reinforcement[J]. Geotechnical Engineering World， 2008， 11(11)： 50－52.

[4] 李志刚， 任佰俪， 秦四清. 高压注浆土钉特性及应用[J]. 岩石力学与工程学报， 2004， 23(9)： 1564－1567. LI Zhi-gang， REN Bai-li， QIN Si-qing. Characteristics and applications of high-pressure grouting soil nailing[J]. Chinese Journal of Rock Mechanics and Engineering， 2004， 23(9)： 1564－1567.

[5] 王立峰， 何俏江， 朱向荣， 等. 土钉墙支护结构综述[J]. 岩土工程学报， 2006， 28(增刊)： 1681－1686. WANG Li-feng， HE Qiao-jiang， ZHU Xiang-rong， et al. Overview of supporting structure of soil nailing walls[J]. Chinese Journal of Geotechnical Engineering， 2006， 28(Supp.)： 1681－1686.

[6] TURNER J P， JENSEN W G. Landslide stabilization using soil nail and mechanically stabilized earth walls： Case study[J]. Journal of Geotechnical and Geoenvironmental Engineering， 2005， 131(2)： 141－150.

[7] EI SAWWAF M A. Strip footing behavior on pile and sheet pile-stabilized sand slope[J]. Journal of Geotechnical and Geoenvironmental Engineering， 2005， 131(6)： 705－715.

[8] SOMMERS A N， VISWANADHAM B V S. Centrifuge model tests on the behavior of strip footing on geotextile-reinforced slopes[J]. Geotextiles and Geomembranes， 2009， 27： 497－505.

[9] 王丽萍， 张嘎， 张建民， 等. 抗滑桩加固黏性土坡变形规律的离心模型试验研究[J]. 岩土工程学报， 2009， 31(7)： 1076－1081. WANG Li-ping， ZHANG Ga， ZHANG Jian-min， et al. Centrifuge modeling of cohesive soil slopes reinforced by stabilizing piles[J]. Chinese Journal of Geotechnical Engineering， 2009， 31(7)： 1076－1081.

[10] THUSYANTHAN N I， MADABHUSHI S P G， SINGH S. Tension in geomembranes on landfill slopes under static and earthquake loading-centrifuge study[J]. Geotextiles and Geomembranes， 2007， 25(2)： 78－95.

[11] ZHANG G， HU Y， ZHANG J M. New image analysis-based displacement-measurement system for geotechnical centrifuge modeling tests[J]. Measurement， 2009， 42： 87－96.

[12] 张嘎， 牟太平， 张建民. 基于图像分析的土坡离心模型试验变形场测量[J]. 岩土工程学报， 2007， 29(1)： 94－97. ZHANG Ga， MOU Tai-ping， ZHANG Jian-min. Displacement measurement using image analysis in centrifuge modeling of slopes[J]. Chinese Journal of Geotechnical Engineering， 2007， 29(1)： 94－97.