超深孔一次成井微差爆破技术研究
李廷春,刘洪强,王超
(山东省土木工程防灾减灾重点实验室 山东科技大学 山东 青岛 266590)
1 引 言
超深孔一次(分段)爆破成井技术即按照筒状硐室断面大小,把所需要的炮孔由上向下钻通(也可以由下向上钻通),而后由下向上全断面一次(分段)爆破成井,爆破完成后,上部支护,下部出矸,随出矸随支护。相对于其它筒状硐室施工方法,具有工期短、费用低、安全性高、施工工序简单等优点,是目前比较先进的筒状硐室施工方法。一般而言,多数筒状硐室的断面大、筒体深,采用一次爆破成井技术时,为了提高炮孔利用率,减小围岩震动破坏,通常采用多段微差爆破技术,实现筒状硐室的分层、分段爆破。由于筒状硐室爆破补偿空间有限,先爆炮孔必须为后爆炮孔的爆破提供合理的补偿空间和爆破自由面,涉及预裂爆破和同分段、相邻分段炮孔微差爆破的起爆时差确定问题。
关于微差爆破技术,许多学者进行了研究[1-10],普遍认为,起爆时差应当是多阶段时间的累加。蒋跃飞[1]认为,起爆时差包括抵抗线内岩石受爆炸应力波压缩作用时间;从压缩作用结束,开始产生裂隙到漏斗边缘裂隙扩展至自由面时间;从岩块开始移动到形成一定宽度裂隙或新自由面的时间。戴俊[2]、黄凯和等[8]、罗开军[10]等定义起爆时差为从起爆到岩渣排出槽腔所经历的时间,并将其分为炸药传播的时间、岩石移动时间、岩渣在槽腔平抛时间和岩渣排出时间4 个阶段。哈努卡耶夫认为,后爆破炮孔在先爆破孔刚好形成爆破漏斗,且爆破岩石脱离岩体形成0.8~1.0 cm 宽的裂缝时起爆为宜。按照上述理论,都有相应的起爆时差计算公式。但这些理论和计算公式没有考虑超深孔爆破的分层、分段爆破问题。由于超深孔一次成井微差爆破需要补偿空间和爆破自由面,因此,需要从超深孔爆破自身特点出发,研究更为合理地起爆时差和起爆顺序。
2 超深孔微差爆破技术的研究
炸药在岩体中爆炸会产生爆炸应力波与爆生气体,超深孔爆破破岩需要它们的综合作用才能完成。由于炸药性能、岩石性质的复杂性,且爆炸作用的时间很短,目前关于微差爆破的基本机制尚无定论。主要存在的假说有:应力波相互干涉假说、自由面假说、剩余应力假说和岩体碰撞学说,其中自由面假说和补偿空间假说,是本次起爆时差计算公式推导所用的主要理论。
2.1 超深孔微差爆破的破岩机制
(1)自由面假说
自由面假说认为,先起爆的炸药在岩体内已造成了某种程度的破坏,如在端部形成了一个新的爆破漏斗;横向形成破碎区和裂隙区等,这些破坏都存在一定宽度的裂隙和附加自由面。新增加自由面一方面增大了应力波的反射几率;另一方面减小了后起爆装药的最小抵抗线,并改变了爆破作用方向,为后起爆装药创造了有利的破碎条件。
(2)补偿空间假说
先起爆的炮孔,首先在爆破动力作用下,形成爆破漏斗,随后槽腔范围内岩石破碎,破碎岩石在高温、高压爆炸气流的作用下,一边沿抵抗线方向高速碰撞槽腔壁面,一边向槽腔外排出。这就为后起爆炮孔在横向和纵向都提供了一定范围的补偿空间,改变了装药段破碎岩石只能靠装药孔提供补偿空间的局面,避免了炮孔底部再生岩的生成。
2.2 超深孔微差爆破时间间隔的确定
超深孔一次爆破成井技术需要计算的微差时间有4 种,包括预裂爆破延期时间,掏槽孔与相邻辅助孔、同分段辅助孔、相邻分段辅助孔的起爆时差。
2.2.1 预裂爆破延期时间1T 的确定
采用预裂爆破的目的是:减小爆破震动对围岩的破坏,保证围岩的稳定性。预裂爆破要求,周边孔首先起爆,在周边孔之间形成贯通裂隙后,其余炮孔再起爆。预裂爆破延期时间1T 可用下式计算:
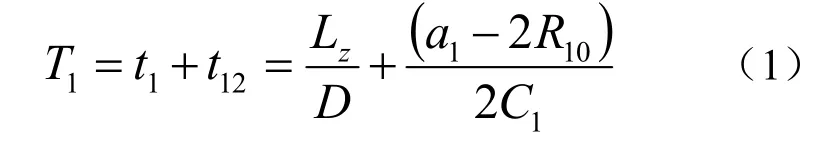
式中: t1为爆轰波或导爆索传播时间(s); t12为相邻周边孔贯通所需要的时间(s); Lz为孔内装药长度(m);D 为孔内平均爆速或导爆索爆速(m/s);a1为周边孔间距(m); R10为粉碎区半径(m); C1为裂隙扩展平均速度(m/s), C1= 0.1CP, CP为应力波传播速度(m/s)。
2.2.2 掏槽孔与相邻辅助孔起爆时差2T 的确定
掏槽孔相邻的辅助孔起爆前,要求掏槽爆破后槽腔内岩石充分破碎,且形成一段空腔,空腔是由于气、固混合体运动前端即抛渣初始段排出槽腔而形成的。
(1)槽腔内岩渣初始段抛出所用时间4t
为分析槽腔的排渣过程,根据掏槽爆破成腔理论,做如下基本假设:①菱形掏槽爆破成腔形状可近似为菱形,气、固混合体为充满整个槽腔且没有间隙的连续介质;②混合体运动过程中受到的主要动力是爆生气体的推力,阻力是槽腔壁的摩擦力;③混合体获得初速度后,在抛出槽腔前做匀加速运动。
爆生气体在气、固混合体中产生的初始冲量BI为

式中:a、b 分别为菱形槽腔对角线长度(m);M为掏槽孔爆破范围内的岩石质量(kg),下端爆破时M 前正负号取正,上端爆破时取负;21t 为岩石充分破碎所需要的时间(s);B 为炮孔间最大间距(m);0P 为槽腔内气、固混合体的初始压力(Pa);r 为掏槽孔半径(mm);0r 为空孔半径(mm);P为爆生气体瞬时压力(Pa);fL 为非装药段长度(m)。
气、固混合体侧向摩擦阻力的冲量fI 为

式中:L0为菱形槽腔边长(m);L 为炮孔深度(m);f 为气、固混合体的侧向摩擦系数;λ 为侧压力系数, λ = μs/ (1 - μs), μs为动态泊松比。
根据冲量定理并结合式(2)、(3),腔内气、固混合体的初速度0V 可表示为

槽腔内气、固混合体所受初始力为

槽腔内气、固混合体加速度为
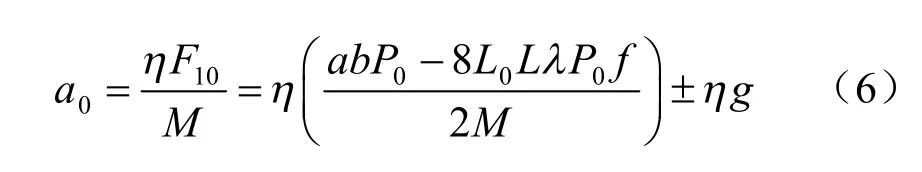
在基本假设的基础上,混合体的运动方程可表示为
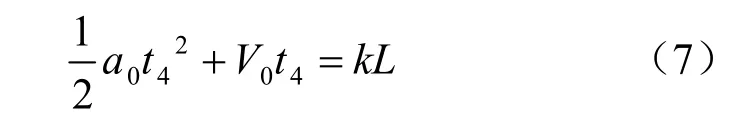
由式(7)可得:

式中:η 为气、固混合体排出初始段前,所受合力的折算系数,η =0.65~0.8;k 为炮孔深度折减系数,kL 即为气、固混合体的初始段长度(m),k 根据爆破漏斗深度等条件确定,取k=0.4。
(2)掏槽孔与相邻辅助孔起爆时差2T
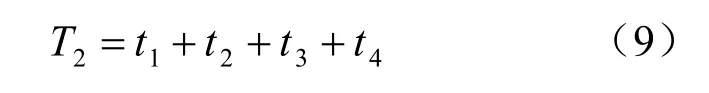
式中: t2=max( t21, t22), t22为刚好形成爆破漏斗的时间(s); t3为岩石移动的时间(自某处自由面上岩石开始移动到或平抛碰撞到对面槽腔壁之间的时间)(s);W 为爆破漏斗深度(m);β 为岩石破碎角(°);X 为炮孔最小抵抗线方向槽腔宽度(m);为平均抛渣速度(m/s)。
2.2.3 同分段辅助孔起爆时差3T 的确定
采用同分段相邻辅助孔微差爆破技术的主要目的是:实现首爆装药为后起爆装药提供横向自由面和补偿空间。时间间隔3T 可用下式计算:

2.2.4 相邻分段辅助孔起爆时差4T 的确定
采用相邻分段辅助孔微差爆破技术的主要目的是:实现首爆装药为后起爆装药提供纵向自由面和补偿空间。时间间隔4T 与2T 计算公式相同,但其中的炮孔深度折减系数k=0.2~0.3。
2.3 起爆顺序的安排
超深孔一次爆破成井通常可分为连续装药爆破成井和分段装药爆破成井。当筒状硐室深度小于5 m,且岩石普氏系数较小时,可以采用连续装药爆破成井技术。
关于起爆顺序,根据超深孔和微差爆破破岩机制,可选用的连续装药爆破成井起爆顺序主要有两种:①预裂爆破时,起爆顺序为:周边孔→掏槽孔→抛渣孔→辅助孔;②光面爆破时,起爆顺序为:掏槽孔→抛渣孔→辅助孔→周边孔。
可选用的分段装药爆破成井起爆顺序,根据周边孔采用预裂爆破或光面爆破,以及下分段和上分段起爆先后顺序的不同,可分为4 种:自下而上预裂爆破、先上下后中间预裂爆破、自下而上光面爆破和先上下后中间光面爆破。另外,具体设置起爆顺序时,为合理利用起爆雷管段数,在保证足够的补偿空间且满足一次最大起爆装药量的条件下,在不同半径上,不同分段炮孔内的装药可以同时起爆。
典型的3 分段爆破成井起爆顺序:自下而上预裂爆破和先上下后中间光面爆破如图1 所示。

图1 典型三分段爆破成井起爆顺序 Fig.1 Detonating sequences of shaft excavation by three-segmented charging blasting
2.4 起爆网络的连接
超深孔一次成井爆破技术,要求各炮孔准确起爆,不能出现拒爆和瞎炮,特别对掏槽孔要求更严。因此,选用并串联电爆网路,即每个炮孔装两发同段并联电雷管,各炮孔之间串联。同时要求发爆器对每个雷管发出的引燃冲量K 大于引爆雷管的引燃冲量。
以上述超深孔一次成井微差爆破理论为指导,完成了华恒矿-650 矸石仓的掘进任务。
3 一次成井爆破方案
3.1 矸石仓场区概况
(3)爆破参数的确定
①分段装药高度的确定
应用利文斯顿爆破漏斗理论和掏槽爆破原理,同时考虑对施工质量和补偿空间的要求,矸石仓采用一次钻孔3 分段装药爆破成井技术,分段高度为:第1、2 分段为2.5 m,第3 分段为4.65 m。
②炮孔布置和单位炸药消耗量的确定
应用岩石爆破理论,并考虑补偿空间的要求,确定辅助孔和周边孔的炮孔间距及抵抗线;掏槽孔的单位炸药消耗量由修正的兰格福斯公式确定。
炮孔布置和炸药消耗量如图2、表2~4 所示。
华恒矿为低瓦斯矿井,-650 矸石仓与-650 西大巷及排矸斜巷相连,上部西大巷为直径4.5 m 的半圆拱巷道,墙高为1.45 m;下部为半径1.85 m 的120°圆弧形巷道,墙高为1.8 m。
现场试验条件为:①矸石仓规格。垂直净高度为9.65 m,掘进直径为4.2 m,荒断面面积为 13.85 m2。②岩层以细砂岩为主,硬度不等,完整性好,未风化,矸石仓所穿越岩石及其岩性如表1所示。③炸药主要性能指标。使用二级煤矿许用小药卷水胶炸药。其性能:爆力为180 ml,爆速为 2 500 m/s;其规格:质量为100 g/个,直径为27 mm,长为150 mm。④现场打眼直径为:空孔为127 mm,其余为75 mm。

表1 -650 矸石仓所穿越岩石及其岩性 Table 1 Rock and lithology of -650 waste rock storage
3.2 爆破方案
采用一次成井爆破技术,即全深度一次钻孔,分段装药,延期起爆,爆破后随支护随出矸。
(1)掏槽方式的选择。为保证爆破效果,充分利用抛渣孔的自由面和辅助抛渣作用,掏槽方式采用由中心抛渣孔和4 个裂槽孔组成的含抛渣孔的菱形掏槽方式,裂槽孔距抛渣孔距离分别为300 mm和400 mm。
(2)延期时间及起爆顺序。采用先上下后中间预裂爆破,电雷管段数为10 段。根据上述起爆时差计算理论,并结合目前常用雷管延期时间,确定所用雷管延期时间分别为0、25、50、75、110、150、200、250、310、380 ms。
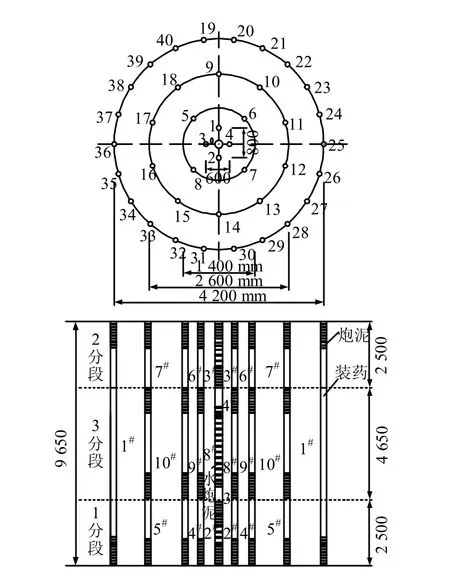
图2 炮孔布置示意图 Fig.2 Arrangement diagrams of blasting hole
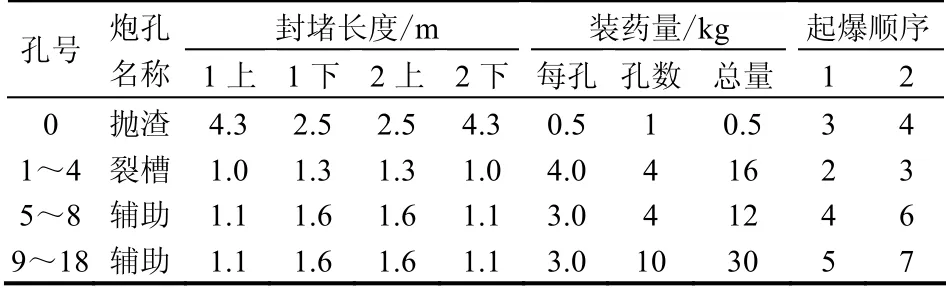
表2 第1、2 装药分段爆破参数表 Table 2 Blasting parameters table of the first and second segments

表3 第3 分段爆破参数表 Table 3 Blasting parameters table of the third segment

表4 周边孔爆破参数表 Table 4 Blasting parameters table of the surrounding holes
3.3 主要成果
(1)爆破后矸石仓成型较好、矸石块度适中,原因在于合理的起爆时差,保证了先起爆炮孔为后起爆炮孔提供了足够的补偿空间和自由面;
(2)围岩爆破震动效应较小,原因在于采用了预裂爆破,并设计了合理的起爆顺序,实现了以上下自由面为起端的分层分段爆破。
4 结 论
(1)基于超深孔微差爆破破岩机制,从理论上推导了一次成井预裂爆破延期时间,以及掏槽孔与相邻辅助孔、同分段辅助孔、相邻分段辅助孔等起爆时差的计算公式;
(2)根据超深孔微差爆破破岩机制提出了连续装药预裂爆破、光面爆破,以及自下而上预裂爆破、先上下后中间预裂爆破、自下而上光面爆破和先上下后中间光面爆破6 种一次成井起爆顺序;
(3)华恒矿通过应用超深孔一次成井微差爆破技术方案,顺利完成了-650 矸石仓的建设任务,爆后矸石块度均匀、围岩稳定、硐室成型好,证明了形成的超深孔微差爆破技术是成功的,其结果对类似工程的实施具有一定的参考价值。
[1] 蒋跃飞. 盲天井深孔爆破一次成井掏槽方式试验研 究[D]. 昆明: 昆明理工大学, 2006.
[2] 戴俊. 直眼掏槽爆破炮眼合理堵塞长度的理论分析[J]. 有色金属, 2001, 53(3): 59-62. DAI Jun. Analyses of rational stemming length for burn-cut blasting[J]. Nonferrous Metals, 2001, 53(3): 59-62.
[3] 翁春林, 叶加冕. 工程爆破[M]. 北京: 冶金工业出版社, 2006.
[4] 张继春. 工程控制爆破[M]. 成都: 西南交通大学出版社, 2001.
[5] 熊代余, 顾毅成. 岩石爆破理论与技术新进展[M]. 北京: 冶金工业出版社, 2002.
[6] 采矿手册编委会. 采矿设计手册[M]. 北京: 中国建筑工业出版社, 1987.
[7] 凌同华, 李夕兵. 基于小波变换的时-能分布确定微差爆破的实际延迟时间[J]. 岩石力学与工程学报, 2004, 23(13): 2266-2270. LING Tong-hua, LI Xi-bing. Time-energy analysis based on wavelet transform for identifying real delay time in millisecond blasing[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(13): 2266-2270.
[8] 黄凯和, 路洪斌, 刘加冬. 多段深孔微差爆破在露天矿中的应用[J]. 化工矿物与加工, 2008, (9): 27-29. HUANG Kai-he, LU Hong-bin, LIU Jia-dong. Application of multiple-row depth holes millisecond blasting in open-pit mine [J]. Industrial Minerals & Processing, 2008, (9): 27-29.
[9] 李存国, 张云鹏. 关于微差爆破合理间隔时间的实践研究[J]. 云南冶金, 2010, 39(2): 22-24. LI Cun-guo, ZHANG Yun-peng. Practical study on logical delay time of millisecond blasting[J]. Yunnan Metallurgy, 2010, 39(2): 22-24.
[10] 罗开军. 孔内孔间微差爆破间隔时间的合理选择[J]. 金属矿山, 2006, (4): 4-6. LUO Kai-jun. Rational selection of delay time in in-hole and between-holes microsecond blasting[J]. Metal Mine, 2006, (4): 4-6.

