海堤地基固结系数反演与工后沉降分形模型预测

秦植海，秦 鹏

（浙江水利水电专科学校 建筑工程系，杭州 310018）

1 前 言

海堤是沿海地区由当地土石材料填筑而成，用来防御台风、抵御海潮的重要水利设施，但我国的海堤工程长期处于缺乏有效监管、维护的状态，海堤的不均匀沉降引起的堤身破坏对沿海地区人民生命安全和经济发展构成了巨大安全隐患[1]。近年来随着相关部门的重视和监测技术的进步，部分地区正在建立或已逐步形成较为系统的海堤沉降监测系统，但没有合理有效的监测分析，监测系统和监测信息无法真正发挥作用，因此，针对海堤特点的理论分析预测模型研究十分迫切[2]。

目前海堤沉降的监测资料分析、预测主要有两种方式：（1）通过监测资料时间序列的变化趋势预测海堤工后沉降的过程，如经验公式法[3]、Asaoka法[4]、灰色理论[5]等已在该领域得到了应用，但这些模型的参数概念并不清楚，缺乏对土体沉降机制上的认识；（2）对采集的土样进行室内土工试验，确定地基土的固结系数后，通过太沙基固结理论推求现场土层沉降过程。由于室内试验条件与现场土层条件、荷载分布情况存在较大差异，且室内土工试验受到取土质量、试样代表性、试验技术水平及计算方法等各因素的影响，造成室内试验得到的固结系数与实际情况有较大出入，从而影响海堤沉降预测结果的可信度[6]。

在海堤实测沉降资料基础上反演计算参数，并以此为依据对后期沉降作出预测，这种反演分析方法能够全面反映现场各要素综合影响，反演得到的固结系数即为整个地基的等效固结系数，实用性强，受到了工程界的重视[7]。在过去的研究中，石名雷等[8]针对具有竖向排水体饱和粉砂土基础沉降问题，进行了固结系数的反演，周健等[9]对分级施加荷载的地基进行了土层参数和固结系数的反演，并进行动态预测，邓永锋等[10]则更深入地将Asaoka法与太沙基一维固结理论耦合，对地基土沉降进行了反演预测。然而，目前的反演分析大多是以公路软土路堤为研究对象，海堤工程具有地质情况复杂、工作环境特殊、修建方法各异的特点，而且由于长期缺乏有效地管理、监测，有效的海堤沉降数据十分有限，因此，针对海堤工程的特殊性对海堤沉降监测资料进行分析具有重要工程实际意义。

本文以浙江省海堤现场工后沉降监测数据为研究对象，运用分层总和法和太沙基一维固结理论对海堤地基土层进行反演，并针对海堤沉降监测数据偏短的特点，尝试引入非线性动力学中的分形理论分析固结系数时间序列，进一步对沿海地区海堤沉降的工后变化趋势进行预测。

2 海堤沉降过程分析基本研究路线

海堤的沉降主要包括堤身的压密变形和地基变形两部分，前者可以通过改进海堤填料和提高施工压实度来控制，且在施工期已大部分完成，后期变形基本由填料的塑性变形引起，在海堤沉降中所占比例极小；后者占海堤总沉降的绝大部分，因此，地基固结变形决定了海堤沉降发展的形态[11]。通过对浙江省宁波、温州、台州、舟山、嘉兴等地区共计34 个海堤（塘）工程地质资料及沉降监测数据进行分析，发现浙江省海堤监测资料具有以下特点：（1）监测主要是以堤顶沉降监测为主，没有对地基进行分层监测；（2）海堤工程没有明确的建设管理单位，造成监测数据主要集中在施工期和施工结束后较短时间内，缺乏长期的沉降监测资料。为了能够有效预测海堤工后长期沉降，提前研判可能发生开裂的堤段，本文建立了海堤沉降过程预测方法，分以下4 个步骤：

（1）以海堤的前期岩土工程勘察及设计资料为依据，利用分层总和法计算海堤最终沉降量，力求在沉降反演中体现地基各层土体的特性；

（2）通过简化土层参数的思想推导海堤的固结系数反演公式，利用海堤沉降监测数据反演计算固结系数；

（3）对固结系数的变化规律进行总结、分析，并在该领域引入具有自相似性的分形模型对具有特殊变化规律的小数据量固结系数序列进行预测；

（4）根据计算得到的地基最终沉降量及固结系数预测时间序列，推求海堤沉降变化趋势，并以工后沉降短期监测值对预测结果加以验证。

3 海堤沉降监测数据的固结系数反演及规律分析

3.1 海堤沉降监测数据的固结系数反演

本文选取施工结束后的监测数据为研究对象，基于分层总和法和太沙基一维固结理论反演该时段的土体固结系数时间序列。海堤沉降监测数据反演主要有以下两个步骤：

（1）分层总和法计算地基最终沉降量

假设地基土是线弹性体，没有侧向膨胀，且土中水及土粒本身的压缩量忽略不计。在外荷载作用下变形只发生在有限厚度的范围内（压缩层）[12]，用分层总和法计算得到地基的最终沉降量tS 。

（2）海堤沉降的固结系数反演

设土体完全饱和，土颗粒和孔隙水不可压缩，单元土体的体积压缩量等于单元体流量之差，根据太沙基一维固结微分方程和竖向固结度计算公式，积分运算可化简得到固结度公式为

整理可得到固结系数：

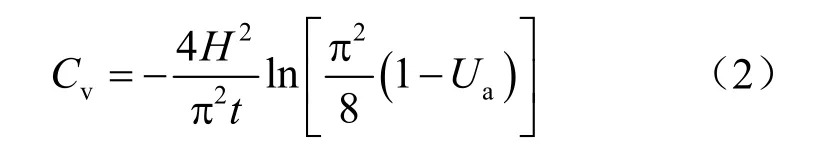
将现场监测的海堤沉降值tS 对应的固结度代入式（2），可反演得到土层的固结系数。

3.2 固结系数规律分析

固结系数vC 作为海堤沉降的关键土工参数，其大小反应了土的压缩性和渗透性，与土的矿物成分和粒度成分有密切的关系，因此，不同监测阶段、不同监测时期得到的固结系数具有很大的差异性。通过推求的固结系数反演公式，对浙江省34 项海堤工程工后沉降数据反演得到的固结系数时间序列进行归类分析发现，固结系数与时间的变化规律大致有以下两种类型：

（1）固结系数随时间增长震荡后趋于收敛。这种类型的数值主要出现在工程结束较长时间后，在文献中一般采用取均值的方法进行计算[7]；

（2）固结系数具有较强的规律性，呈逐渐增加或减小的趋势。这种类型的数值主要出现在施工结束后的较短时间内，由于外部荷载的施加刚刚结束，固结系数还处于一种不稳定的变化状态。这类固结系数的传统求解方法仍为取均值，但由于固结系数时间序列呈非线性的变化趋势，简单的均值求法势必会对沉降的预测值造成影响，产生误差，按固结系数变化趋势，采用合适的预测模型反演土层实际固结系数，进而进行海堤工后沉降预测十分必要。

由于海堤工程缺乏长期的监测数据，具有较强趋势性的固结系数时间序列存在长度较短，数据受到白噪干扰的特点，传统的预测方法如灰色理论、神经网络等对这一类的数据处理效果并不理想，因此，尝试引入分形理论对具有趋势性的固结系数进行分析、预测。在以往的研究中发现，分形理论具有自相似性的特点，能充分挖掘数据本身的信息，对小数据量趋势性数据具有较强的预测效果[13]。

4 改进变维分形模型在趋势性固结系数时间序列预测中的应用

分形理论是Mandelbort 于20 世纪70 年代中期创立的，它基于部分与整体的自相似性，直接从非线性复杂系统的本身入手，分析研究对象的自身性质和规律[13]。分形理论的提出，为揭示隐藏于混乱复杂现象中的精细结构和定量地描述系统提供了理论基础，并在众多领域得到应用[14]。在过去的研究中发现，岩土体可以被看做复杂的非线性动态系统，分形维数可以定量地对岩土体变形进行描述[15－16]，本文在前人研究的基础上，尝试在海堤沉降分析领域引入分形预测模型，对具有较强趋势性的小数据量固结系数时间序列进行预测，并利用式（1）计算得到海堤工后长期沉降过程曲线，以期对海堤工后的管理、维护工作提供重要的参考依据，提前研判可能发生开裂的堤段，采取预防措施。

4.1 常维分形和变维分形

常用的分形模型主要有常维分形和变维分形两种。目前应用的常维分形可用如下幂指数分布定义[13]：

式中：r 为特征线度；N 为与r 有关的数量；C 为待定常数；D 为分维数

当D 为常数时，在双对数坐标上表现为一条直线，可以通过变化求出分维数，即

针对常维分形无法处理双对数坐标上的非直线函数关系的问题，引入了变维分形的概念，其分维数D 不再是常数，而是特征线度r 的函数[14，17]：

N 与r 之间的任意函数关系 N = f ( r)均可转化为变维分形的形式[17]，即使 f ( r ) = C / rD，得到变维分形公式为

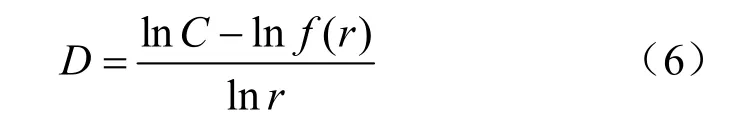
4.2 海堤工后沉降的改进及变维分形模型建立

由于自然界中严格意义上满足常维分形的现象是不存在的，所以大量数值模型需要用变维分形的方法进行计算，但当数据复杂时，变维分形中的函数式又往往庞大而难于计算。研究证明，对于任意函数关系 N = f ( r)都可以转换成常维分形N= C / rD的形式，即将数据进行一系列的变换，使变换后的数据能用常维分形处理，即通过构造1 阶、2阶、3 阶……累积和的分段变维分形模型，然后选择效果最好的变换并确定相应的分形参数[18]，基于此思想，本文利用改进变维分形模型对趋势性海堤固结系数进行预测，进而反演海堤地基沉降值。该模型的具体建立步骤如下：

（1）将趋势性固结系数时间序列点( Ni， ri) (i= 1，2，… ，n )绘于双对数坐标上，将 Ni排成一个基本序列，即

（2）根据基本序列构造其他序列。

按照下面的规则，通过逐阶累加的方法构造监测数据的累积和时间序列：

其中， i = 1，2，…， n。

（3）建立各阶累积和的变维分形模型。

（4）比较各阶累积和变维分形模型，选择最为平顺的累积变换曲线确定分形阶数，对选定的分形维数时间序列曲线插值，拟合计算出分形参数[21]。

（5）根据选定的分形维数带入改进变维分形模型，对固结系数时间序列趋势项进行预测，将固结 系数预测值代入式（1），即可对海堤沉降的监测数据演化趋势进行预测。

5 工程实例

为了验证固结系数反演分析及分形模型预测的可靠性，采用浙江省洞头县北岙后二期东围堤工程的海堤监测数据作为研究对象进行验证计算。

岩土工程勘察报告显示，该海堤地基在钻探深度范围内共揭示3 个大土层，其中第1 土层可细分为3 个亚层。分布特征详见表1。

表1 钻探深度范围内的土层特征[22] Table 1 Characteristics of soil from different horizons[22]

选取洞头北岙后二期东围堤工程0+100 测点2007 年3 月至2008 年12 月间22 个沉降监测数据作为分析对象，此时海堤沉降处于变形发展阶段，原始沉降监测数据间隔时间为一个月。取前15 个点作为计算数据，后7 个数据用以检验，为方便计算，以监测数据的时间先后进行编号， 1，2，r= …，可以得到海堤沉降时间序列如图1 所示。结合岩土工程勘察资料，取影响土层的深度为20 m，通过室内压缩试验计算得到最终沉降量tS 为500 mm，据式（2）反演得到固结系数时间序列如图2 所示，可以看到固结系数呈趋势性增长。

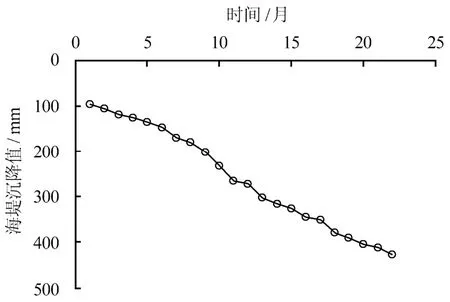
图1 洞头北岙后二期东围堤工程0+100 测点 沉降时间序列 Fig.1 Settlement time series of Beidaihou second east-causeway project in 0+100 monitoring point

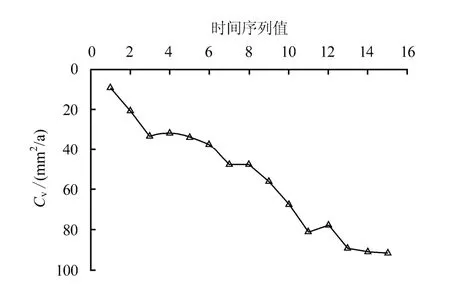
图2 洞头北岙后二期东围堤工程0+100 测点 固结系数时间序列 Fig.2 Inversed consolidation coefficient time series of Beidaihou second east-causeway project in 0+100 monitoring point

引入改进变维分形预测模型，对反演得到的固结系数时间序列进行分析。首先根据计算步骤，对时间序列进行1～4 阶累积和构造，分别求出固结系数的各阶分维值，如表2 所示。

为了便于直观地分析和选取，将表2 数据绘制于图3，可以看到 3D 、 4D 系列值拟合效果都比较理想，特别是 3D 曲线在后半段十分平顺。因此，本文选取 3D 曲线作为预测模型的分形参数曲线，对曲线的分段分形维数进行拟合、反推，得到模型的趋势项序列如表3 所示。

表2 洞头北岙后二期东围堤工程0+100 测点固结系数 变维分形维数计算结果 Table 2 Results of n-order variable-dimensional fractal sequences of Beidaihou second east-causeway project in 0+100 monitoring point

图3 固结系数各阶变维分形维数汇总 Fig.3 N-order variable-dimensional fractal sequences

表3 固结系数预测值时间序列 Table 3 The prediction of consolidation coefficients

通过改进变维分形模型可对固结系数的趋势值进行预测，利用式（1）计算可得到海堤工后短期、长期沉降曲线如图4、5 所示。由图4 可以看出，分形模型预测结果与实际观测结果在工后短期内吻合度较好，由长期沉降预测曲线可以看出，固结变形随时间增长逐渐完成，本工程工后2 年内土层的固结度接近于1，海堤软土地基的沉降基本结束，沉降曲线符合土体沉降的变化规律。

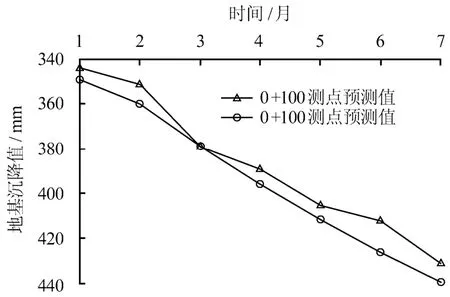
图4 0+100 测点短期沉降预测值与实测值对比曲线 Fig.4 Prediction of short-term settlement in 0+100 monitoring point

图5 0+100 测点长期沉降预测值与实测值对比曲线 Fig.5 Prediction of long-term settlement in 0+100 monitoring point

5 结 论

（1）以浙江省海堤工程现场采集的短期监测数据为基础，利用改进变维分形预测模型对土层固结系数进行了分析，并通过预测出的固结系数趋势项对海堤地基长期沉降过程进行了预测，为海堤工程的工后维护、管理提供了参考依据，与传统方法相比，该方法反演得到现场土层固结系数并用非线性理论对长期沉降进行预测，避免了由室内试验得到固结系数的不准确性，又比经验公式更能反映出实际土体的固结机制，其结果更加真实可信。

（2）针对具体工程，使用本文方法对海堤不同测点的实测沉降数据进行反演、预测，即可得到海堤不同测点的沉降量与时间s-t 关系曲线，进一步可绘制出多条不同测点相同时间n-s 关系线，相邻测点沉降差较大时，即预示着该时段此处海堤发生开裂的可能较大。通过这种方法就可以做到提前预测、提前处理，达到减小工程隐患的目的。

致谢：特别感谢浙江省围垦局及浙江省各市县水利局在本次省水利厅海堤专项课题研究中提供的宝贵现场资料。

[1] 黄铭， 刘俊. 海堤渗压监测因果模型基本结构和因子选择[J]. 上海交通大学学报， 2008， 42(11)： 1931－1934. HUANG Ming， LIU Jun. The frame of sea wall osmosis pressure monitoring model and factors selection[J]. Journal of Shanghai Jiaotong University， 2008， 42(11)： 1931－1934.

[2] 潘翔， 黄铭， 王跃威. 海塘渗压监测分析的时间序列组合模型[J]. 岩土力学， 2006， 27(8)： 1374－1378. PAN Xiang， HUANG Ming， WANG Yue-wei. The time series model of seawall osmotic pressure monitoring analysis[J]. Rock and Soil Mechanics， 2006， 27(8)： 1374－1378.

[3] 包太， 刘新荣， 朱凡， 等. 固结系数的最小二乘法计算[J]. 岩土工程学报， 2005， 27(10)： 1230－1232. BAO Tai， LIU Xin-rong， ZHU Fan， et al. Least square method for the consolidation coefficient evaluation[J]. Chinese Journal of Geotechnical Engineering， 2005， 27(10)： 1230－1232.

[4] 王志亮， 黄景忠， 李永池. 沉降预测中的Asaoka 法应用研究[J]. 岩土力学， 2006， 27(11)： 2025－2032. WANG ZHi-liang， HUANG Jing-zhong， LI Yong-chi. Study on application of Asaoka's method to settlement prediction[J]. Rock and Soil Mechanics， 2006， 27(11)： 2025－2032.

[5] 臧德彦. 灰色系统理论在海堤沉降预测中的应用[J]. 测绘工程， 1999， 8(2)： 50－54. ZANG De-yan. Application of the theory of gray system to forecast the dam subsidence forecasting[J]. Engineering of Surveying and Mapping， 1999， 8(2)： 50－54.

[6] 张仪萍， 张晓海. 室内固结系数的一种推算方法[J]. 岩土工程学报， 2002， 24(5)： 616－618. ZHANG Yi-ping， ZHANG Xiao-hai. A method for evaluating coefficient of consolidation[J]. Chinese Journal of Geotechnical Engineering， 2002， 24(5)： 616－618.

[7] 周健， 闫东霄， 贾敏才， 等. 某深水港土层固结系数反演及工后长期沉降预测[J]. 岩土力学， 2008， 29(5)： 1407－1410. ZHOU Jian， YAN Dong-xiao， JIA Min-cai， et al. Back analysis of consolidation coefficient of soils and prediction of long term post-load settlement of a deep- water port[J]. Rock and Soil Mechanics， 2008， 29(5)： 1407－1410.

[8] 石名磊， 赵俊明， 鲁安顺. 高速公路地基沉降反演分析[J]. 东南大学学报(自然科学版)， 2005， 5(4)： 589－592. SHI Ming-lei， ZHAO JUN-ming， LU An-shun. Back- calculation of ground settlement for freeway[J]. Journal of Southeast University( Natural Science Edition)， 2005， 5(4)： 589－592.

[9] 周健， 白彦峰， 贾敏才. 某矿石码头堆场矿石分级压载的地基沉降预测[J]. 岩土力学， 2009， 30(7)： 2101－2104. ZHOU Jian， BAI Yan-feng， JIA Min-cai. Prediction of foundation settlement of a heap of ore-port under multi- stage loading during period of use[J]. Rock and Soil Mechanics， 2009， 30(7)： 2101－2104.

[10] 邓永锋， 刘松玉， 洪振舜. 基于沉降资料反演固结系数的方法研究[J]. 岩土力学， 2005， 26(11)： 1807－1809. DENG Yong-feng， LIU Song-yu， HONG Zhen-shun. Back analysis of consolidation coefficient with in-situ settlement data[J]. Rock and Soil Mechanics， 2005， 26(11)： 1807－1809.

[11] 章定文， 刘松玉. 试论连云港海相软土路堤沉降规律[J]. 岩土力学， 2006， 27(2)： 304－308. ZHANG Ding-wen， LIU Song-yu. Settlement features of embankment of Lianyungang marine clay[J]. Rock and Soil Mechanics， 2006， 27(2)： 304－308.

[12] 钱家欢， 殷宗泽. 土工原理与计算[M]. 北京： 中国水利水电出版社， 1996.

[13] MANDELBROT B B. Les objets fractals： Forme， hasard et dimension[M]. Paris： Flammarion， 1975.

[14] MANDELBROT B B， EVERTSZ C J G， JONES P W. Fractals and chaos： The mandelbrot set and beyond[M]. New York： Springer， 2004.

[15] 秦鹏， 秦植海. 基于分形理论的岩质高边坡监测资料分析[J]. 水利水运工程学报， 2008， 9(3)： 92－97. QIN Peng， QIN Zhi-hai. Analysis of high rocky slope monitoring data based on fractal theory[J]. Hydro-Science and Engineering， 2008， 9(3)： 92－97.

[16] 薛天放， 杨庆， 栾茂田. 基于GIS 技术的滑坡空间分布的分形特征研究[J]. 岩土力学， 2007， 28(2)： 347－354. XUE Tian-fang， YANG Qing， LUAN Mao-tian. Research on fractal characters of spatial distribution of landslide based on GIS[J]. Rock and Soil Mechanics， 2007， 28(2)： 347－354.

[17] MANDELBROT B B. Fractal analysis and synthesis of fracture surface roughness and related forms of complexity and disorder[J]. International Journal of Fracture， 2006， 138， 13－17.

[18] 付昱华. 变换形成的分形与海洋环境数据分析预测[J].海洋通报， 2000， 19(1)： 79－88. FU Yu-hua. Transform-formed fractals and analyses and forecast of marine environment data[J]. Marine Science Bulleten， 2000， 19(1)： 79－88.

[19] 秦鹏. 基于非线性理论的高边坡监测数据分析与预测[D]. 合肥： 合肥工业大学， 2009.

[20] 秦鹏， 秦植海. 岩质高边坡监测数据的改进变维分形预测模型[J]. 水利水运工程学报， 2010， 3(1)： 90－94. QIN Peng， QIN Zhi-hai. Forecasting model of monitoring data of rock high slope based on improved variable dimension fractal theory[J]. Hydro-Science and Engineering， 2010， 3(1)： 90－94.

[21] 秦鹏，张喆瑜，秦植海等.滑坡体监测数据的改进变维分形-人工神经网络耦合预测模型[J].长江科学院院报， 2012， 29(3)： 29－34. QIN Peng， ZHANG Zhe-yu， QIN Zhi-hai， et al. IVDFANN prediction model on monitoring data of landslide deformation[J]. Journal of Yangtze River Scientific Research Institute， 2012， 29(3)： 29－34.

[22] 秦植海， 秦鹏， 方荣. 浙江省典型海堤工后沉降分析报告[R]. 杭州： 浙江省围垦技术中心， 浙江水利水电专科学校， 2009.