山区高填方地基蠕变沉降特性及 简化计算方法探讨

宋二祥，曹光栩

（清华大学 土木工程系土木工程安全与耐久教育部重点实验室，北京 100084）

1 引 言

自从我国西部大开发战略实施以来，西部山区的基础设施建设发展迅速，由此出现不少山区填方地基工程，涉及机场、铁路、公路等众多领域。这些填方工程的突出特点是填方体量大、高度高，且常存在软弱地基[1]。对于此类山区高填方工程，很重要的一是要保证其稳定，二是能预测和控制其沉降变形，特别是工后沉降变形。而后者是一个很有难度的问题，涉及原地基可能的固结变形、原地基和填方体的蠕变变形、湿化变形等。对于固结变形已有较多的研究，但对于山区常见块碎石填方体蠕变变形的研究目前还不够深入。沈珠江是国内较早开展块碎石蠕变研究的学者之一，早在1988 年他就针对堆石坝变形问题开展了块碎石（堆石料）蠕变试验[2]，并建议采用双曲线来近似刻画蠕变应变随时间发展的规律。随后河海大学、长江科学研究院等单位也对碎石蠕变进行了大量研究[3－4]。但目前广泛应用的仍是沈珠江建议的双曲线模型。

双曲线模型是针对应力为常值的情况给出的。但实际高填方地基是分层填筑，且对于高填方地基来说很需要预测填方完成不久后的工后沉降，这一时间相对于填方施工工期不是很长，这就需要较为细致地考虑施工工期内分层填筑的时间过程，对于下层填方体来说，也就涉及到逐级分期加载条件下蠕变变形的计算问题。这可能是高填方地基与土石坝工程的一个重要不同点。

本文首先在前人已有的研究基础上，对碎石的蠕变特性、蠕变模型进行简要的讨论，并提出一些改进建议，随后在双曲线模型的基础上提出一种可以考虑荷载随时间变化条件下高填方地基蠕变变形的简化计算方法，并根据试验结果对其合理性进行了初步的计算验证。同时，通过对室内干湿循环试验结果进行分析，发现碎石料的干湿循环变形与其循环次数关系明显，在此基础上又进一步提出了蠕变变形与干湿循环变形的耦合计算方法。最后应用上述所提方法对一高填方工程实例进行了计算分析。

2 碎石土蠕变特性及对现有模型的 讨论

沈珠江等[2]于1988 年针对土石坝的变形问题进行了堆石料的三轴剪切蠕变试验，讨论了蠕变变形随时间发展的规律。尝试分别用下列对数函数、指数函数及双曲线函数来拟合试验给出的蠕变变形-时间曲线：

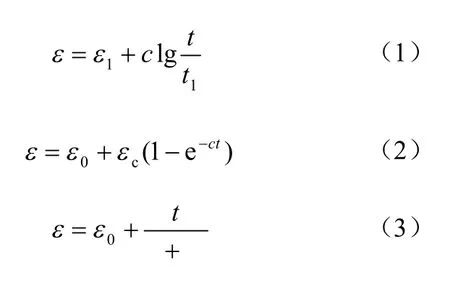
式中：a、b、c 和cε 为由材料及荷载特性决定的常数，0ε 、1ε 分别为t =0 和t =t1时刻发生的应变（可含有瞬时应变和蠕变应变，取决于时间起始点的选择）。显然，式（1）为2 参数模型，式（2）、（3）为3 参数模型。通过与试验结果对比发现，对于给定应力状态，堆石料的变形一般随时间趋于稳定值，故式（1）在理论上说不适用。而式（2）的对应曲线在开始阶段变形发展过慢，与实际相差较大，而吻合最好的是式（3），即双曲线。

分析双曲线函数不难看出，1/a 实际是t＝0 时的蠕变速率，1/b 为时间无限长时土样在0ε 基础上再增加的蠕变变形。沈珠江进而通过数据拟合给出双曲线模型的3 个参数。采用其所具有的有限数据进行拟合的过程显示：

（1）初始蠕变速率1/a 变化不大，与应力间无确定关系，可近似假定为常数；

（2）0ε 随剪应力比增大而按双曲线规律增大；

（3）最终蠕变应变量1/b 随剪应力比及围压增大而增大。 由上述（1）、（3）两点可推知如下的第（4）点： （4）应力水平以及围压越高，蠕变完成所需时间越长。

表1 是使用其所给参数计算的不同试验条件下完成最终蠕变量90%所需要的时间，表中计算结果很好地证明了第（4）点推论。另外，还可以看出，对于饱和土样在同等应力水平下完成蠕变所需时间比干土样要长。

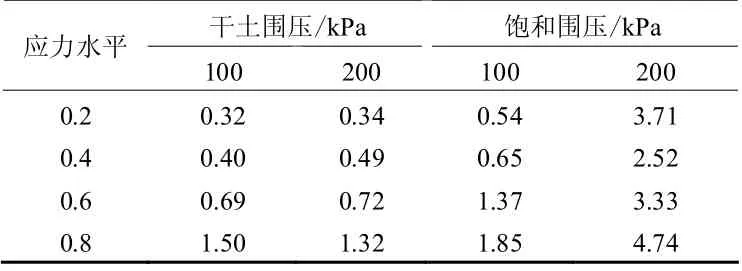
表1 不同应力水平下完成90%最终蠕变量 所需时间 (单位：h) Table 1 Time required for completing 90% of the final creep under different stress levels (unit: h)

根据饱和土固结的经典理论[5]可知，饱和软土主固结变形完成的时间在理论上与荷载大小无关，而由上面数据可以看出，土体的蠕变变形（次固结变形）完成时间则与荷载水平关系较大。蠕变变形是在土骨架承担有效荷载不变的情况下，由于土体颗粒发生错动翻转、滑移破碎，位置进行重新排列而引发的。在同等初始条件下，应力水平越高，土颗粒排列得将会越密实，达到的最终状态也将会越稳定，即最终蠕变量也会越大。上面第（1）点结论提到的不同应力水平下初始蠕变速率变化不大，可以这样解释，当应力水平增大时增加了土颗粒发生滑动的动力，但同时所达到的压缩状态也更密实，从而也将会使阻止土颗粒移动的摩擦阻力增大，总体上两者增加的程度大致相同，所以不同应力水平下的初始蠕变速率变化不大。最终蠕变量随应力水平增大，而蠕变速率基本不变，结果必然导致完成蠕变时间的延长。

通过进一步的思考，还可指出以下几点：

（5）双曲线模型仅适用于蠕变收敛的情况，比如大面积水平成层填方体的蠕变沉降问题，对其他一般问题可能并不适用；

（6）为便于确定0ε ，应明确取其为土体某一应力状态建立后不长时间内所发生的应变，亦即理论上的瞬时应变。在这一前提下，本文建议用邓肯-张模型所给模量计算0ε 的值，而对一维压缩问题则可用压缩回弹曲线来进行计算。对于各层填方体在其自身填筑过程中的变形，包括其自身重量作用及夯实作用等引起的变形，是无法计算也不用计算的，因为我们这里是计算填筑完成后的土层变形。

（7）由于试验数量有限，沈珠江文中并未提到密实度、级配、岩石风化程度等对蠕变模型参数的影响。一般来说，粗粒料的密实度越高、级配越好、岩石的风化程度越低其最终蠕变量将会越小[6－8]，但如果要实现准确的量化计算仍需要进一步细致的研究；

（8）从沈珠江的试验数据看，应变达到稳定值所需时间很短，仅约200 h，即不到10 d 时间（240 h以后蠕变完成量已达到了99.8%以上），这就意味着用此模型来计算实际工程问题，蠕变完成的时间也同样不会长。但实际上，现场高填方地基蠕变变形发展的过程要长得多，比如西北口堆石料面板坝，观测沉降最大的点在施工完成时的沉降为36 cm，8年后发展到66 cm[9]；王华俊等[10]根据九寨黄龙机场竣工后5 个月的沉降监测数据认为，次固结完成时间需要3～5 年。也有研究者指出，室内试验条件下蠕变完成的时间较现场要短[11]。仔细分析可以发现，实际现场条件下填方体还要经受晴雨反复和温度升降等外界环境因素的影响，变形的大小及发展持续时间会远大于实验室的测试结果。其中，雨水或地下水的反复浸润是一个重要因素。国内外已有不少学者开展了针对碎石料的湿化变形研究，国外如Sowers 等[12]、Anthiniac 等[13]、Nobari 等[14]，国内如殷宗泽[15]、朱俊高[16]、李广信[17]等。其中在试验研究方面，殷宗泽等[15]用大型三轴仪进行了干湿循环作用下堆石料蠕变变形的研究，并得出结论，认为干湿循环变形占堆石料后期变形的主要部分。现场条件下碎石料的干湿循环变形与地下水或雨水的浸润程度有密切关系，实际观测资料多是综合了各种变形因素在内的变形，无法准确判定干湿循环变形的大小，因此，对于碎石等粗粒料干湿循环变形的研究还应以可控条件下的室内试验为主要手段，依据试验曲线建立合适的模型来刻画干湿循环变形，同时与现场实际浸润发展规律相对比，最后将此变形作为附加蠕变变形进行计算。

3 荷载变化情况下蠕变变形的计算

在上述双曲线模型基础上，针对大面积填方问题，本文给出一个考虑蠕变过程中荷载变化的计算方法，其要点如下：

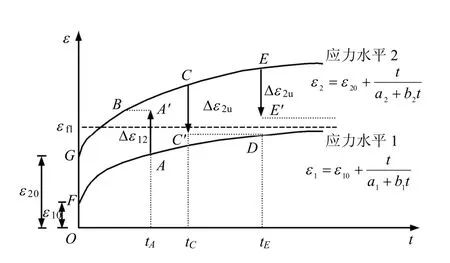
图1 考虑荷载变化的蠕变变形简化计算方法示意图 Fig.1 Schematic diagram of simplified calculation method for creep under varying loads

（1）对于给定应力状态（荷载）下的一薄层土单元，其蠕变变形随时间按一确定的双曲线规律发展，其起始时刻从与该应力状态对应的瞬时变形发生后计算。图1 给出2 个不同应力水平下土层的蠕变变形随时间发展的曲线。

（2）当该土单元所受荷载从某一值增加到一较大值时，首先可计算由此荷载增量引起的瞬时应变增量，随后的蠕变将沿着与该较大荷载对应的双曲线从应变等于如上增加后的应变值处开始继续发展。如图1 所示，设该土单元的蠕变从应力水平1对应曲线的A 点因荷载增加到水平2 而增加瞬时变形 12εΔ 后变化到A′点，可找到应力水平2 对应曲线上与A′应变相同的B 点，此后的变形将自B 点沿曲线2 发展。

（3）若该土单元所受荷载从某一值减小到一较小值时，同样可计算一瞬时应变增量（此时为回弹），随后的蠕变将沿着与该较小荷载对应的双曲线从应变等于如上减小后的应变值处开始继续发展。如图1 所示，设该土单元的蠕变变形沿着曲线2 由点B发展到点C 时荷载减小至应力水平1，可从总变形中减去瞬时回弹变形 2uεΔ 后得到C′点，再找到曲线1 上与C′点等应变的D 点，此后的蠕变将自D 点沿曲线1 发展。如果如上减小后的应变值大于该较小应力水平对应的终极应变，比如图1 中从点E 开始荷载降低，减小后的应变仍大于曲线1 的渐进值εf1，则认为蠕变停止，这其中隐含的一假定是认为蠕变为不可恢复的。

利用侧限固结仪针对西部山区常用到的灰岩碎石料进行了不同荷载级别下的蠕变试验，并对试验结果用双曲线模型进行拟合，得到相关计算参数如表2 所示。

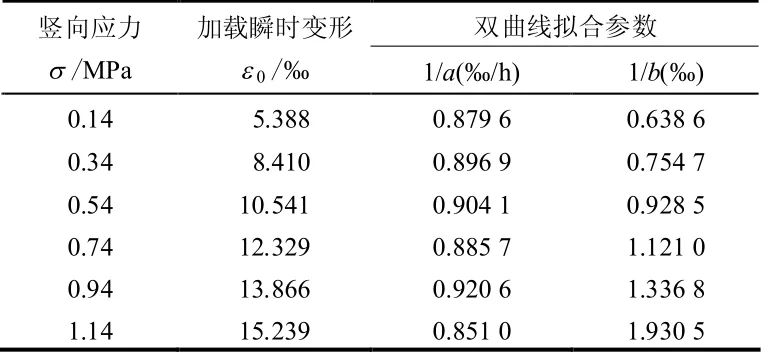
表2 不同荷载级别下双曲线模型计算参数 Table 2 Calculation parameters of hyperbolic model under different load levels

从表2 中可以看出，在侧限试验条件下不同应力水平时初始蠕变速率1/a 同样变化不大，这点与前面所提到的沈珠江试验结果相同，因此，也可以近似假定1/a 为常数；而最终蠕变量1/b 以及瞬时变形0ε 则与应力水平关系较大，基本上是随着竖向应力的增大而增大的。首先，对于瞬时变形0ε 可以通过应力增量与相应应力水平下的变形模量计算得到，而变形模量的计算则可以参照邓肯-张模型中初始模量的计算方法采用下式[18]：

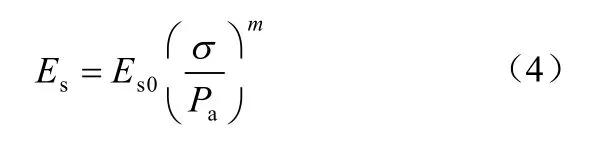
式中： Pa为标准大气压，量纲与竖向应力σ 相同；Es0为σ = Pa时的模量值，m 为试验常数。当计算由较低级荷载 σ1增加到较高级荷载 σ2时的瞬时变形值 Δε12时计算公式如下：

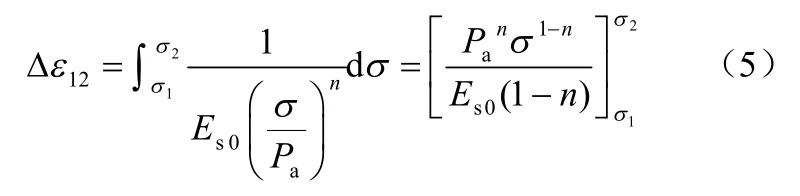
其次，通过分析发现，最终蠕变量1/b 与竖向应力σ 之间的关系用指数函数拟合较为合适：

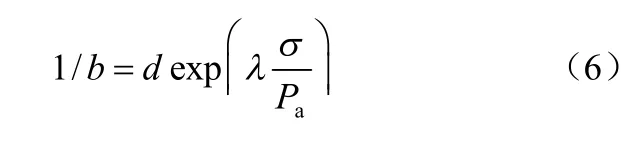
式中：d 和λ 为试验参数。对于此次试验所用灰岩碎石料，平均密度ρ=2.02 g/cm3，Es0、n、d 和λ 分别取44.38 MPa、0.513 4、0.506 5、和0.115 0。得到试验参数后采用前面所述方法对分级加载蠕变试验进行全过程模拟，结果如图2 所示。

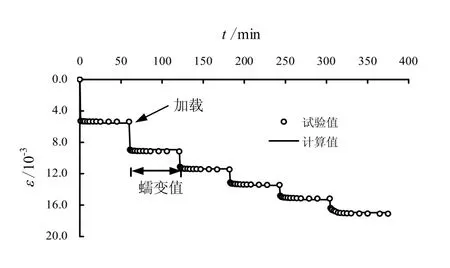
图2 蠕变变形简化算法计算值与试验值对比 Fig.2 Comparison between experimental values and calculated values obtained by creep calculation method

4 蠕变变形与干湿循环变形的耦合计算方法

图3 是利用大型侧限固结仪参照文献[15]中的方法对西南山区常见石灰岩碎石料进行的普通蠕变和干湿循环变形试验的典型试验结果对比，其中干湿循环次数为5 次，排水后放置时间间隔设为1 h。从中可以看出，相同应力水平下碎石料在有限的几次干湿循环作用下的变形与普通蠕变变形相比，其后期增长趋势依然很明显，这也进一步验证了干湿循环作为一种影响碎石料长期变形的重要因素是不能忽视的，尤其对于工后沉降控制较为严格的山区高填方工程。

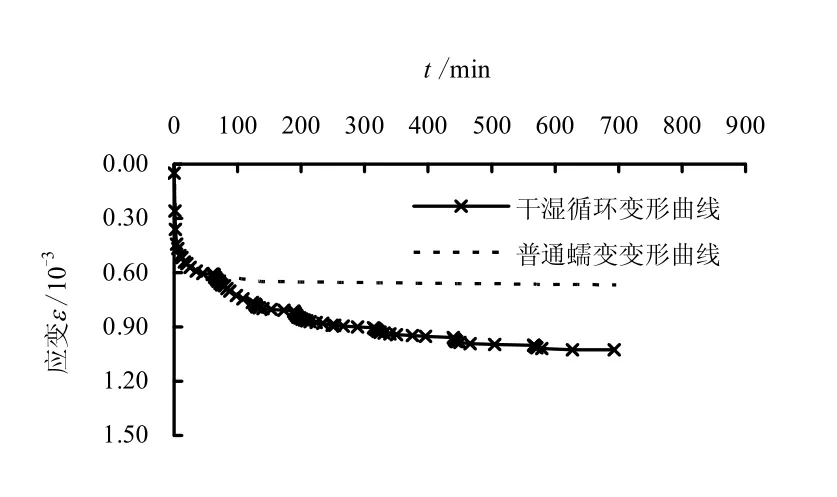
图3 1.14 MPa 应力水平下干湿循环变形与 普通蠕变曲线对比 Fig.3 Routine creep test curve and dry-wet cycle test curve of rockfills under 1.14 MPa

用图3 中干湿循环作用下的变形值，减去普通蠕变变形值，所得结果可以近似认为是该试验应力水平下仅由干湿循环所引起的变形，用同样方法也可以得到其他应力水平下仅由干湿循环作用所引起的变形曲线，如图4 所示。

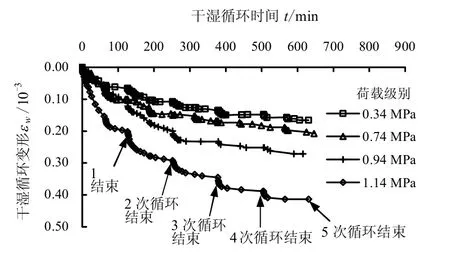
图4 碎石料干湿循环变形曲线 Fig.4 Test curves of rockfills only due to dry-wet cycles under different loads

从图可以看出，一方面干湿循环作用引起的变形随应力水平的提高逐渐增大；另一方面，碎石料在后面几次循环中每次浸水初期变形有相对较大的增长，而后变形快速趋于稳定，整体上呈现出类似于台阶状的变化，并且应力水平越高这种现象越明显。既然试验结果显示碎石料的干湿循环变形与干湿循环次数n 关系较明显，因此，就可以把循环次数n 作为变量来刻画碎石料在干湿循环作用下的变形，如图5 所示。

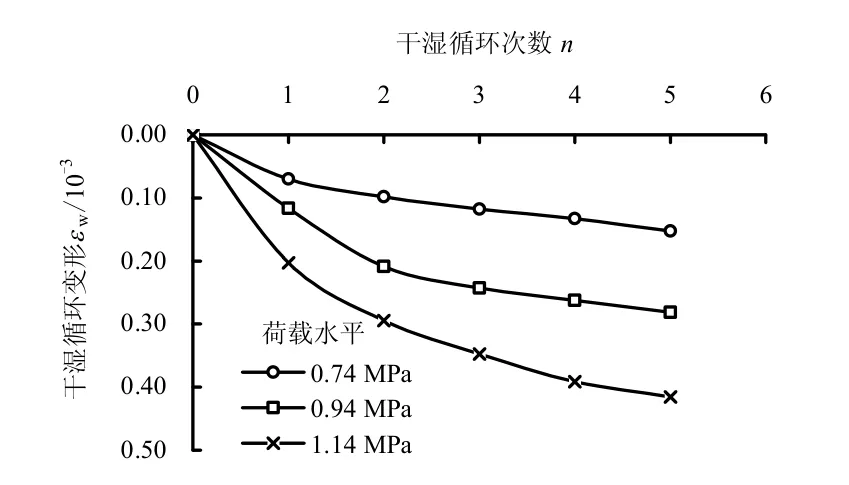
图5 不同荷载下碎石料干湿循环变形-循环次数n 曲线 Fig.5 Relationships between dry-wet cycle deformation of rockfills and cycle numbers under different loads

通过用不同的经验函数模型对图5 中的试验数据进行拟合对比，发现用式（7）给出的对数函数来计算碎石料的干湿循环变形效果相对较好：

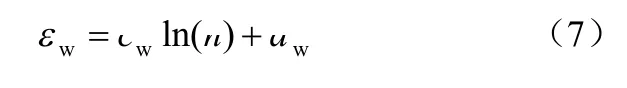
式中：cw和dw为由材料及荷载特性决定的试验参数。

这里之所以采用对数函数而非如前采用双曲线函数，其根本原因在于干湿循环引起的变形随循环次数的累积而趋于稳定的过程较长，也就是说它随循环次数的增加而发展的速率衰减较慢。而双曲线函数相对很快便趋于稳定，在工程所关心的时段内不能很好拟合变形的发展规律。诚然，对数函数是不收敛的。但随着自变量的增大，它的变化率毕竟还是有着明显的衰减。而在工程实际中，当变形发展速率小于一定值时即可忽略，也就是说，在实际工程中式（7）不会用于n 值很大的情况。

对于式（7）中的试验参数，经对试验数据进行分析发现，cw与应力水平之间近似呈对数关系，dw与应力水平间可用幂函数关系来描述：

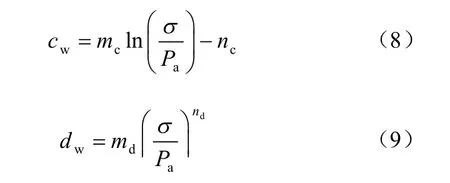
式中：mc、nc、md和nd为拟合参数，对于本试验所用灰岩碎石料，平均密度ρ=2.02 g/cm3，mc、nc、md和nd分别为0.195 3、0.333 6、0.54×10-3和2.449。利用上述计算公式和拟合参数对灰岩碎石料在不同应力水平下的干湿循环变形进行拟合计算，计算值与试验值对比如图6 所示。

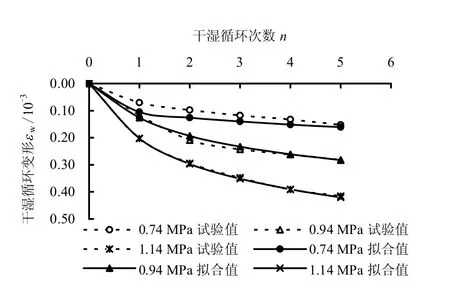
图6 拟合不同荷载下碎石料干湿循环变形-循环次数曲线 Fig.6 Fitting curves of dry-wet cycle deformation with cycle numbers under different loads

在室内试验条件下，可以人为控制干湿循环在较短的时间内完成，但在现场条件下完成这一循环需要较长时间，可以近似认为实际条件下碎石填料经历一次强降雨过程即为完成一次干湿循环。因此，现场条件下碎石填料经历的强降雨次数也就是其所经历的干湿循环次数。在考虑干湿循环作用引起的变形计算中可以统计填方工程所在场区多年强降雨分布规律，然后用较为合适的函数将强降雨次数n与时间t 联系起来，这样就可以用实际时间来计算碎石填料的干湿循环变形。下面以云南某机场填方工程为例进行说明。

由云南某机场场区多年的气象统计资料[19]可直接得到每月降雨的毫米数，而后根据国家气象局公布的降雨标准将其折算为当月的强降雨次数，这样就可以得到表3。进而假定每月内的强降雨次数在该月内均匀分布，则由表3 所给数据可以得到图7 所示1 年内该场区累计降雨次数∑n 与时间t 的关系曲线，而这曲线可用式（10）给出的分段线性函数来近似描述。当计算时间超过1 年后，可以把下1 年1 月1 日作为起点按此函数重复计算，并注意累加上1 年计算出的降雨次数。由某一时间段内的依据强降雨次数，再用式（7）～（9）即可计算干湿循环引起的变形。

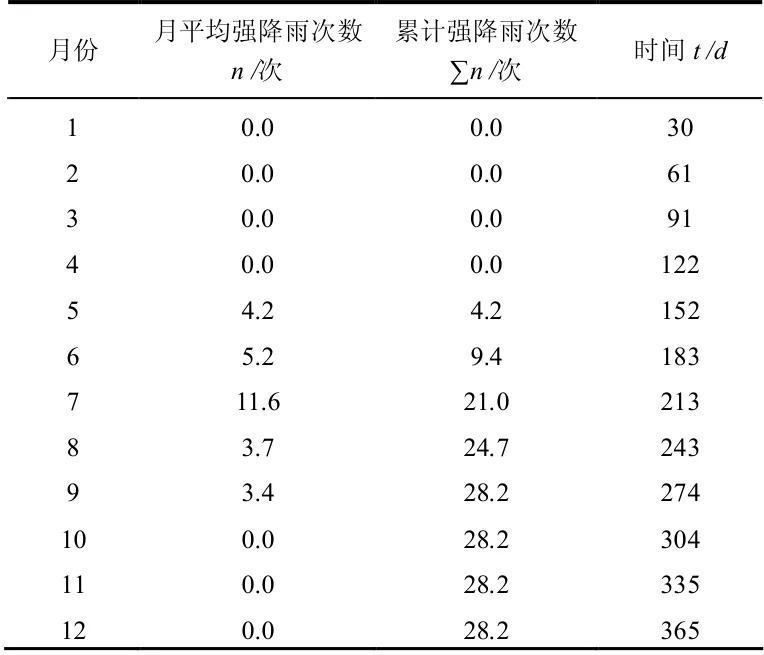
表3 云南某机场场区强降雨统计规律[19] Table 3 Statistical heavy rainfall in some regions of Yunnan

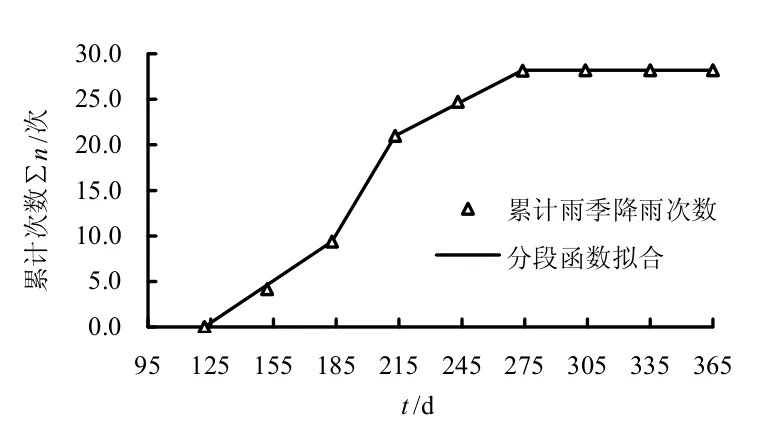
图7 一年中降雨累计次数∑n-时间t 关系曲线 Fig.7 Relationship curve between annual cumulative rainfall numbers and time

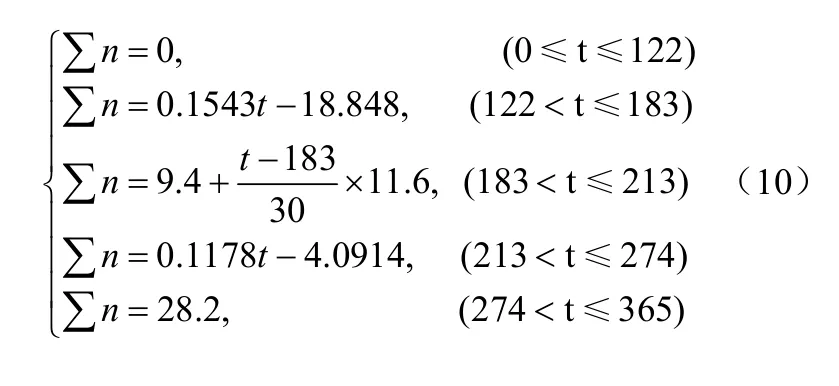
碎石料在干湿循环作用下发生较大变形的原因，一方面是由于雨水或地下水的反复浸润导致颗粒强度的降低，在荷载作用下发生碎石料部分颗粒的破碎细化，引起颗粒排列的调整；另一方面是由于水分的润滑作用导致颗粒接触部位的摩擦系数降低，从而使原来处于摩擦平衡状态的颗粒之间发生进一步的错动滑移。而已有研究表明，碎石料蠕变变形产生的原因也正是来自于碎石颗粒的破碎和滑移[20－21]，两种变形发展的最终效果都是碎石料越来越密实，可以说某一变形值（无论哪种变形）对应着碎石料的某一密实状态，当碎石料密实到一定程度这两种变形必然都会停止或达到可以忽略的程度。因此，干湿循环变形的发生必然会使后面蠕变变形可发展的空间减小，同样蠕变变形的不断发展也必将影响再次发生的干湿循环变形的大小，两种变形其实是相互耦合在一起的。基于这种理解，这里提出了一种能可以考虑两种变形之间相互影响的简化算法。

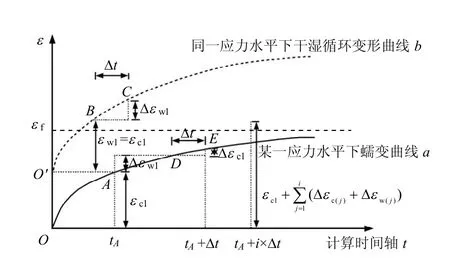
图8 蠕变变形和干湿循环变形耦合计算示意图 Fig.8 Coupling computing diagram about creep and dry-wet cycle deformation

（1）对于给定的某一应力状态（荷载）下的一薄层土单元，当尚未发生干湿循环变形时，土单元的变形随时间沿一给定双曲线发展，如上图曲线a中由点O 到点A 所示；曲线b 则对应单独的干湿循环变形，其起始时刻O′与土单元第1 次发生干湿循环变形时刻相对应。

（2）当到达点A 时发生干湿循环变形，则令干湿循环变形初值 εw1等于现在已经发生的变形值εc1，利用式（7）计算出一等效的初始干湿循环次数n1。

（3）取一较短的时间间隔Δt，通过式（10）所给降雨曲线计算tA到tA+Δt 内发生的干湿循环次数Δn1，而后通过式（7）计算由n1到n1+Δn1期间干湿循环所增加的变形量 Δεw1。

（4）再把（εc1+ Δεw1）作为此时的总变形，找到曲线a 上与之对应的一点D，此后的蠕变变形就是从D 点开始沿曲线a 向后发展，根据曲线a 计算时间Δt 内的蠕变值 c1εΔ 。

（5）在总的时间轴中只计入一次Δt，但在tA+Δt内发生的总变形计为（c1ε +εΔ +c1εΔ ），因为干湿循环变形和蠕变变形是同时发生的，而从前面试验结果可以看出，干湿循环变形发展得更为迅速，所以上步计算令干湿循环变形先发生来影响同一时段内的蠕变变形以较好模拟实际变形过程。

（6）若以后还有干湿循环发生即按上面（2）～（5）步骤重复进行；如果到第i 次进行计算时总变形 c1ε +∑(w()tεΔ +c()tεΔ )的值等于或超过了蠕变变形双曲线的渐进值fε 则，认为蠕变变形不再发生，而只发生干湿循环变形。

需要说明的是上面所提出的干湿循环变形与蠕变变形的耦合简化算法还仅是一种粗略地考虑两种变形在发展过程中相互影响的方法，计算结果严格来讲是偏于保守的，更为精确的耦合计算方法尚需要进一步细致的研究。

5 实例计算

对于大面积水平成层的高填方地基，可以按其实际填筑过程进行分层，取每层土体中心部位的应力代表该层的应力水平，利用上面第3、4 节中提出的方法计算每层填土从其自身填筑完成之后的蠕变变形及干湿循环变形，需要注意每层填土计算的起始时刻是不同的。

为了方便应用，按照上述方法编制了计算高填方长期工后沉降变形的程序，并对云南某机场一标段中道槽区填方地基进行了工后沉降计算。该标段道槽区所用填料基本为中微风化碎石料，所选计算断面填方高度约40 m，计算时根据实际碾压厚度每1 m 分为一层，填筑至设计标高耗时大约330 d[22]，利用该程序计算工后两年内的沉降变形发展情况，结果如图9 所示。

图9 云南某机场某标段道槽区工后沉降计算结果 Fig.9 Calculated post-construction settlements of a road zone in some airport in Yunnan

从图9 中可以看出，在没有其他环境因素影响的前提下，该处道槽区工后沉降变形在最初的大约3 个月里发展较快；之后当进入工后第1 个雨季时由于降雨的影响，变形速率明显增大，雨季过后沉降速率又恢复到较低水平；在经历2 个雨季后蠕变变形和降雨引起的干湿循环变形基本都趋于稳定。工后2 个雨季完成时蠕变变形和干湿循环变形在已发生的道槽区工后沉降中所占的比重列于表4。可见对于本算例在第1 个雨季结束时，蠕变变形占到了填方体工后沉降的71.83%，干湿循环变形占28.16%，此后随着填方体经历雨季的增多干湿循环变形所占比例逐渐增大。由此可知，为较好预测工后变形的发展情况，对2 种变形均需认真计算。

表4 蠕变与干湿循环变形在工后沉降中所占比重 Table 4 Proportions of creep and dry-wet cycle deformation in the post-construction settlement

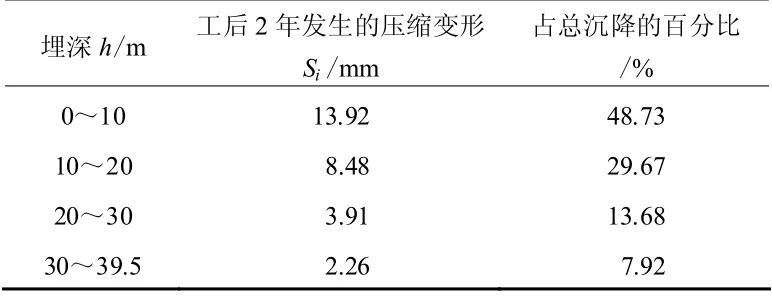
表5 不同埋深部位填筑体发生的工后压缩变形（2 年） Table 5 Post-construction compression deformations of fill foundation in different depths (two years)

表5 则展示了上面所计算的填方体不同埋深部位发生的工后压缩变形在总沉降中所占的比重。从表中可以看出，对于施工期较长、分层填筑而成的填方体其不同埋深部位的土体对工后沉降的贡献是不同的。先填筑的土体虽然最终的应力水平较高，但在施工过程中经过多次的加载压缩和多个施工间歇期的发展其密实程度已经较高，蠕变变形以及干湿循环变形中的大部分已经完成，而新填筑的土体变形历时较短，蠕变变形和干湿循环变形基本还处于较快发展阶段，较多的变形将在工后完成，因此，最终会导致上部填筑体的变形对工后总沉降贡献较大。基于此认识，建议在施工中对较晚填筑的粗粒填料需要特别加强填筑质量管理，可以考虑增大碾压次数或强夯能级，如果条件允许还可以在施工间歇期对填方地基重点部位的填料采用堆载预压处理，以增大其密实程度，促使其蠕变以及干湿循环变形较多在施工过程中完成。

由于目前该机场高填方工程监测的持续时间还较短，因此，还不能利用长期监测资料对上列结果进行检验，但从已有工程经验粗略来看，上述计算结果大体上是合理的。

6 结 论

（1）本文依据自己及他人的研究，通过深入的思考、分析，进一步解释了块碎石填方体的蠕变机制，得到一些对解决实际问题有直接帮助的认识。

（2）基于室内试验结果和对蠕变机制更深入的认识，对双曲线模型的特点、应用条件以及参数的影响因素等进行了探讨。

（3）在原有双曲线模型的基础上，针对大面积填方地基给出了一个考虑蠕变过程中荷载变化的计算方法，并通过计算对比展示了其合理可行性；

（4）室内试验结果表明，与同应力水平下的蠕变变形相比，干湿循环作用引起碎石料的变形是相当可观的，并且后期增长趋势依然明显；干湿循环变形值随循环次数n 的增加呈现出台阶状的变化规律。

（5）在分析室内试验和碎石料干湿循环变形机制的基础上，提出了能够考虑给定降雨情况的蠕变变形和干湿循环变形的简化耦合计算方法，并就一工程实例进行了计算讨论。

需要指出的是本文所提出的蠕变变形和干湿循环变形简化计算方法目前还只是针对大面积填方问题的一维计算方法，对于如何计算荷载发生变化的复杂应力状态下的三维蠕变变形和干湿循环变形将是下一步的工作重点，成果将会另文发表。

[1] 徐则民， 黄润秋， 许强. 九寨黄龙机场填方高边坡静力稳定性分析[J]. 地球与环境， 2005， 33(增刊)： 290－295. XU Ze-min， HUANG Run-qiu， XU Qiang. Three dimensional finite element analysis of some high fill slope stability [J]. Earth and Environment， 2005， 33(Supp.)： 290－295.

[2] 沈珠江， 左元明. 堆石料的流变特性试验研究[C]//第六届土力学及基础工程学术会议论文集. 上海： 同济大学出版社， 1991： 443－446.

[3] 梁军， 刘汉龙， 高玉峰. 堆石蠕变机制分析与颗粒破碎特性研究[J]. 岩土力学， 2003， 24(3)： 479－483. LIANG Jun， LIU Han-long， GAO Yu-feng. Creep mechanism and breakage behaviour of rockfill [J]. Rock and Soil Mechanics， 2003， 24(3)： 479－483.

[4] 程展林， 丁红顺. 堆石料工程特性试验研究[J]. 人民长江， 2007， 38(7)： 110－114. CHENG Zhan-lin， DING Hong-shun. Test research on engineering properties of rockfill [J]. Yangtze River， 2007， 38(7)： 110－114.

[5] 陈仲颐， 周景星， 王洪瑾. 土力学[M]. 北京： 清华大学出版社， 1994.

[6] 刘宏， 张倬元. 四川九寨黄龙机场高填方地基变形与稳定性系统研究[M]. 成都： 西南交通大学出版社， 2006.

[7] 傅华， 凌华， 蔡正银. 粗颗粒土颗粒破碎影响因素试验研究[J]. 河海大学学报（自然科学版）， 2009， 37(1)： 75－78. FU Hua， LING Hua， CAI Zheng-yin. Influencing factors for particle breakage of coarse grained soil [J]. Journal of Hohai University (Natural Sciences)， 2009， 37(1)： 75－78.

[8] 李国英， 米占宽， 傅华. 混凝土面板堆石坝堆石料流变特性试验研究[J]. 岩土力学， 2004， 25(11)： 1712－1716. LI Guo-ying， MI Zhan-kuan， FU Hua. Experimental studies on rheological behaviors for rockfills in concrete faced rockfill dam [J]. Rock and Soil Mechanics， 2004， 25(11)： 1712－1716.

[9] 殷宗泽. 土工原理[M]. 北京： 中国水利水电出版社， 2007.

[10] 王华俊， 韩文喜， 赵其华. 高填方地基沉降回归参数模型探讨[J]. 土工基础， 2004， 18(3)： 43－45. WANG Hua-jun， HAN Wen-xi， ZHAO Qi-hua. Discussion about regression parameter model of settlement for high embankment [J]. Soil Engineering and Foundation， 2004， 18(3)： 43－45.

[11] 殷宗泽. 高土石坝的应力与变形[J]. 岩土工程学报， 2009， 31(1)： 1－14. YIN Zong-ze. Stress and deformation of high earth and rockfill dams [J]. Chinese Journal of Geotechnical Engineering， 2009， 31(1)： 1－14.

[12] SOWERS G F， WILLIAMS R C， WALLACE T S. Compressibility of broken rock and the settlement of rockfills [C]//Proc. 6th Int. Conf. on Soil Mech. and Foundation Eng. Toronto： University of Toronto Press， 1965， 2： 561－565.

[13] AHNTINIAC P， BONELLI S. Modeling saturation settlements in rockfill dams[C]//Proceedings of the International Symposium on New Trends and Guidelines on Dam Safety. Barcelona： Taylor& Francis， 1998， 2(6)： 17－19.

[14] NOBARI E S， DUNCAN J M. Movements in dams due to reservoir filling[C]//Proceedings of Performance of Earth and Earth Supported Structures. California： University of California， 1972： 797－816.

[15] 王海俊， 殷宗泽. 堆石料长期变形的室内试验研究[J].水利学报， 2007， 38(8)： 914－919. WANG Hai-jun， YIN Zong-ze. Experimental study on deformation of rockfill material due to long term cyclic wetting-drying [J]. Journal of Hydraulic Engineering， 2007， 38(8)： 914－919.

[16] 魏松， 朱俊高. 粗粒料湿化变形三轴试验中几个问 题[J]. 水利水运工程学报， 2006， 1： 19－23. WEI Song， ZHU Jun-gao. Discussion on some problems in triaxial wetting test of coarse-grained materials [J]. Hydro-Science and Engineering， 2006， 1： 19－23.

[17] 李广信. 堆石料的湿化试验和数学模型[J]. 岩土工程学报， 1990， 12(5)： 58－64.

[18] 李广信. 高等土力学[M]. 北京： 清华大学出版社， 2004.

[19] 昆明市气象局. 昆明小哨国际机场场址航空气象条件分析研究报告[R]. 昆明： [s. n.]， 2009.

[20] COOP M R， SORENSEN K K， BODAS F T. Particle breakage during shearing of a carbonate sand [J]. Geotechnique， 2004， 54(3)： 157－163.

[21] 梁军， 刘汉龙. 面板坝堆石料的蠕变试验研究[J]. 岩土工程学报， 1998， 24(2)： 1－6. LIANG Jun， LIU Han-long. Creep test for rockfill of CFRD[J]. Chinese Journal of Geotechnical Engineering， 1998， 24(2)： 1－6.

[22] 昆明新机场建设指挥部. 全场地基处理与土石方工程施工图设计说明及施工技术要求[R]. 昆明： [s. n.]， 2008.