亚黏土典型剖面电阻率-含水率关系模型研究

杜鹏辉，余建民，赵贵章

(华北水利水电大学 地球科学与工程学院， 河南 郑州 450046)

亚黏土(又称粉质黏土)是介于黏土和砂土之间的一种地基土，其粒径较黏性土大，存在结核体，可塑范围较小，因其同时具有砂土液化性和黏土的触变性，从而存在极大的工程安全隐患。因而，对于亚黏土类不稳定地质剖面的入渗及水分运移研究而言，如何快速、准确的搞清其水分运移规律是非常重要的。目前研究土体水分赋存的主要方法有原位检测和物理模型试验。原位检测虽然精度比较高，但仅能反映局部问题；而物理模型试验虽然反映比较比较全面，但误差性较大。基于此，高密度电阻率成像法(ERT)逐渐被应用于水文地质等领域。高密度电阻率成像法是以岩土类介质的电性差异为基础，通过观测和研究人工建立的地下稳定电场的分布规律，来解决环境和工程地质等问题的一种方法。其具有观测精度高、数据采集量大、地质信息丰富、生产效率高等特点。因此，该方法目前广泛应用于地质、构造、水文地质、工程地质勘察等方面，解决了诸多实际问题，在工程上发挥了极大的作用。

关于土的电阻率模型，20世纪40年代，Archie[1]最先把土的电阻率与结构联系起来并提出适用于饱和砂岩的电阻率模型，随后Waxman和Smits[2]在进行含油页岩地层的研究中，把电阻率法应用其中，并建立了表面导电性良好的非饱和黏性土的电阻率模型，自此电阻率法开始广泛的应用于岩土工程中。

进入21世纪，电阻率法在工程应用中有了长足的发展。国内广大学者根据实际研究，利用电阻率法推导软土、黏性土、砂土等土体的电阻率模型，并利用这些模型来定量的分析各类土体的工程特性，结构变化规律及对不良地质条件进行评价，均达到了良好的效果[3-7]。

近些年来，高密度电阻率法的出现，使其应用更加广泛。黄佳坤等[7]利用高密度电法建立淡水和浅海水域的地质模型，通过研究证实高密度电法在水底隧道勘察应用中效果突出。刘庭发等[8]、闫亚景等[9]分别在研究常规物理模型和超重力离心环境中的水分运移量测和天然边坡水分运移规律方面应用高密度电法技术，通过构建电阻率与含水率的关系，有效的揭示出水分运移规律。张泰丽等[10]亦采用高密度电阻率成像法，利用数学形式构建电阻率与含水率的关系模型，有效的验证各模型在探究天然粉质黏土边坡水分运移规律中的有效性。

此外，由于高密度电阻率法在工程上的准确、方便、快捷。此技术还在研究垃圾填埋场的滤液运移规律、地震后不稳定斜坡研究、河道淤泥质土电阻率变化本质研究、珊瑚岛礁研究、探测出水库渗流通道的位置及高程和土石复合介质电阻率特性影响因素等方面的研究有着广泛的应用[11-14]。

显然，电阻率与含水率的变化情况在反映介质水分赋存状态方面效果显著。因此，在典型地质剖面的水分运移规律研究中，选用高密度电阻率法构建含水率与电阻率模型，并作进一步分析是非常有必要的。本文以涡河典型地质剖面为研究对象，采用高密度电阻率成像(ERT)技术，通过监测获取剖面土体的电阻率与含水率的散点数据，在前人的基础上进一步拟合构建二者的关系模型，并筛选验证，从而讨论各个模型的有效性和实用性。

1 试验区域及试验方案

1.1 剖面概况

该典型剖面位于沱河(安徽宿州段)，试验点位于宿州的东南郡，距离宿州城区4 km的沱河节制闸下游20 m处的河漫滩上。该地高程在20 m～30 m之间，平原地区，地形平坦，河道周边为良田。试验场地表面覆盖有效植被，上覆土层约3.7 m为棕黄、棕红色亚黏土，含大量铁锰质浸染，铁锰质、钙质结核；下伏浅褐色粉砂、粉细砂及亚砂土，松散、分选性良好，主要成分为石英、长石。该典型剖面结构如图1所示。

图1 典型剖面示意图

1.2 高密度电阻率法检测原理

高密度电阻率成像法作为一种重要检测手段，被广泛应用于地质研究领域中。它以岩土体的导电性为基础，施加外在电流，通过检测被研究岩土体对应电场的变化情况，来得到相应的电阻率的变化规律。在试验区域，为了检测到岩土体介质深部的电阻率变化规律，通过逐步改变电极之间的检测距离的途径，来达到相应的目的。其原理图如图2所示。

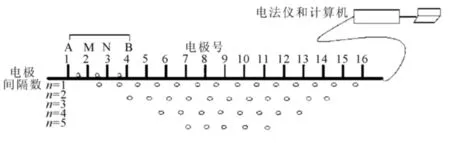
图2 实验原理图

1.3 研究方案

为了掌握剖面含水率的空间分布特征，在水分入渗试验中采用无线传输的水分、水势传感器监测入渗过程中水分的变化规律。水分传感器主要监测地表0.05 m、0.10 m、0.20 m、0.30 m、0.50 m、1.00 m等6个位置的含水率变化过程。水势传感器主要监测0.10 m、0.20 m和0.30 m三个位置的水势变化，规定数据采集时间间隔为1 h。试验点水文地质参数仪器的布置示意图如图3所示。

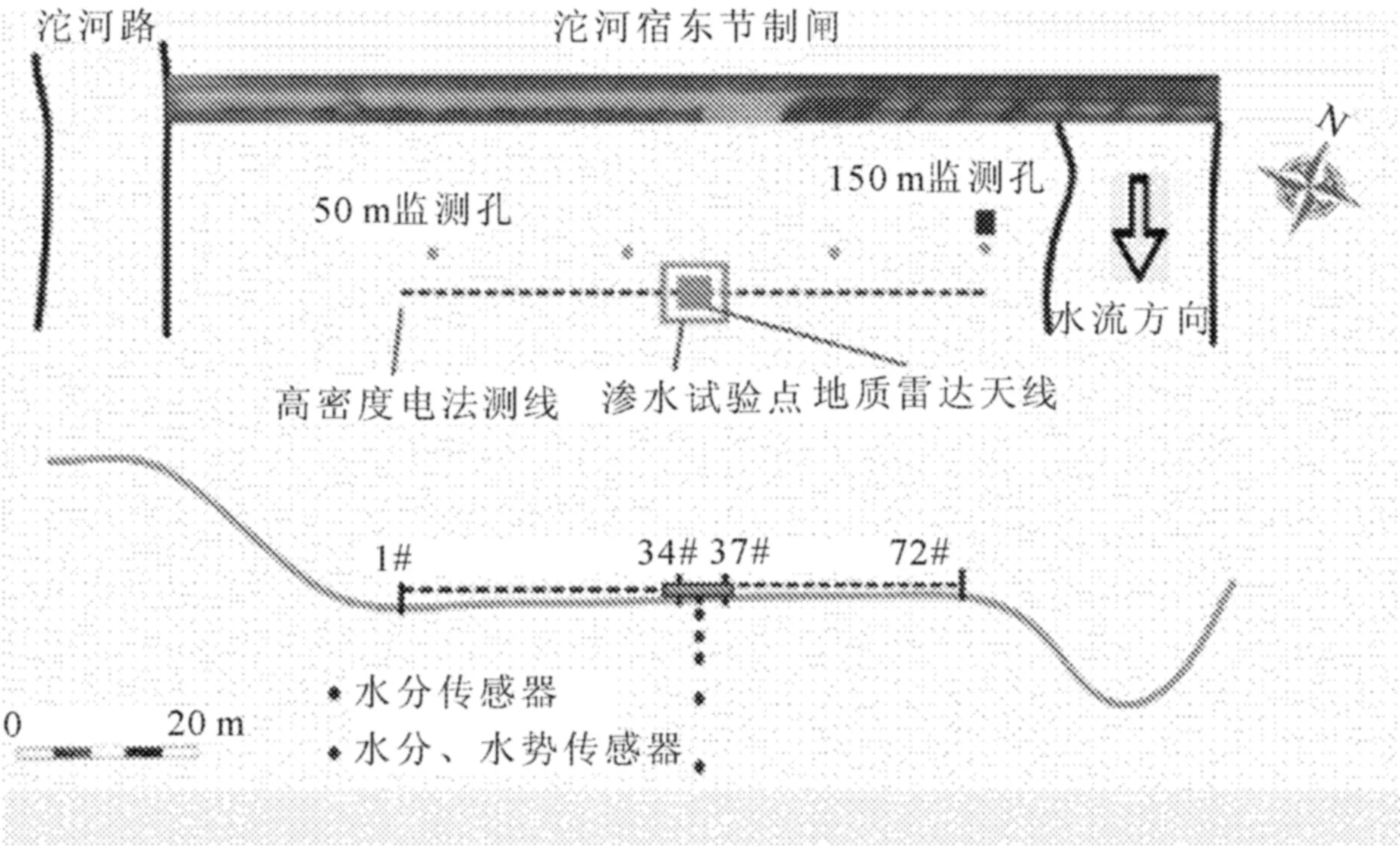
图3 水文地质参数布置示意图

为了研究剖面含水率的空间分布状况，利用高密度电法监测渗水试验过程中水分入渗过程，布置测线长度36 m，极距0.5 m。在使用高密度电法监测水分入渗过程时，首先测定入渗前剖面的电阻率特征，其次，在开始渗水试验的过程中监测2次～3次，且在试验结束后应每天监测2次～3次，并持续3 d～4 d。依据不同时间、不同埋深、不同水势变化下的电阻率、含水率试验实测数据，结合实际的勘察资料来对比分析各类模型在剖面应用中的实用性和有效性。

2 结果分析

2.1 含水率与电阻率随埋深变化特征及不同时间水势大小的分析

通过对野外钻孔资料及试验报告成果的综合分析，在埋深小于3.7 m的范围内，该剖面岩性主要以亚粘土为主，含大量铁锰质浸染，夹杂少量铁锰质、钙质结核，粒径2 mm～8 mm不等。试验过程中，选择未扰动的场地进行入渗测量，电阻率测试(ERT)中外界温差变化不大，所以本文认为测量剖面电阻率的变化主要是由于涡河水势大小导致含水率变化引起的。

图4为整理的土体电阻率随埋深的变化曲线。从总体趋势上来看，在有效深度的范围内，不同时刻剖面土体的电阻率随深度的增加呈现先增大后减小的趋势，即电阻率从近地表的84 Ω·m～108 Ω·m开始增加，在埋深0.75 m处出现极大值376 Ω·m，并开始呈下降趋势，随后在1.75 m处出现第一个极小值165 Ω·m，之后在埋深大于1.75 m后一直下降。尽管从总体上看电阻率变化趋势相似，但随着时间的变化电阻率随深度的变化速率并不一致，最明显的埋深0.75 m处，9月22至23日测量值仅在331 Ω·m～328 Ω·m之间，差异并不大，而9月21日值达到364 Ω·m～376 Ω·m之间。

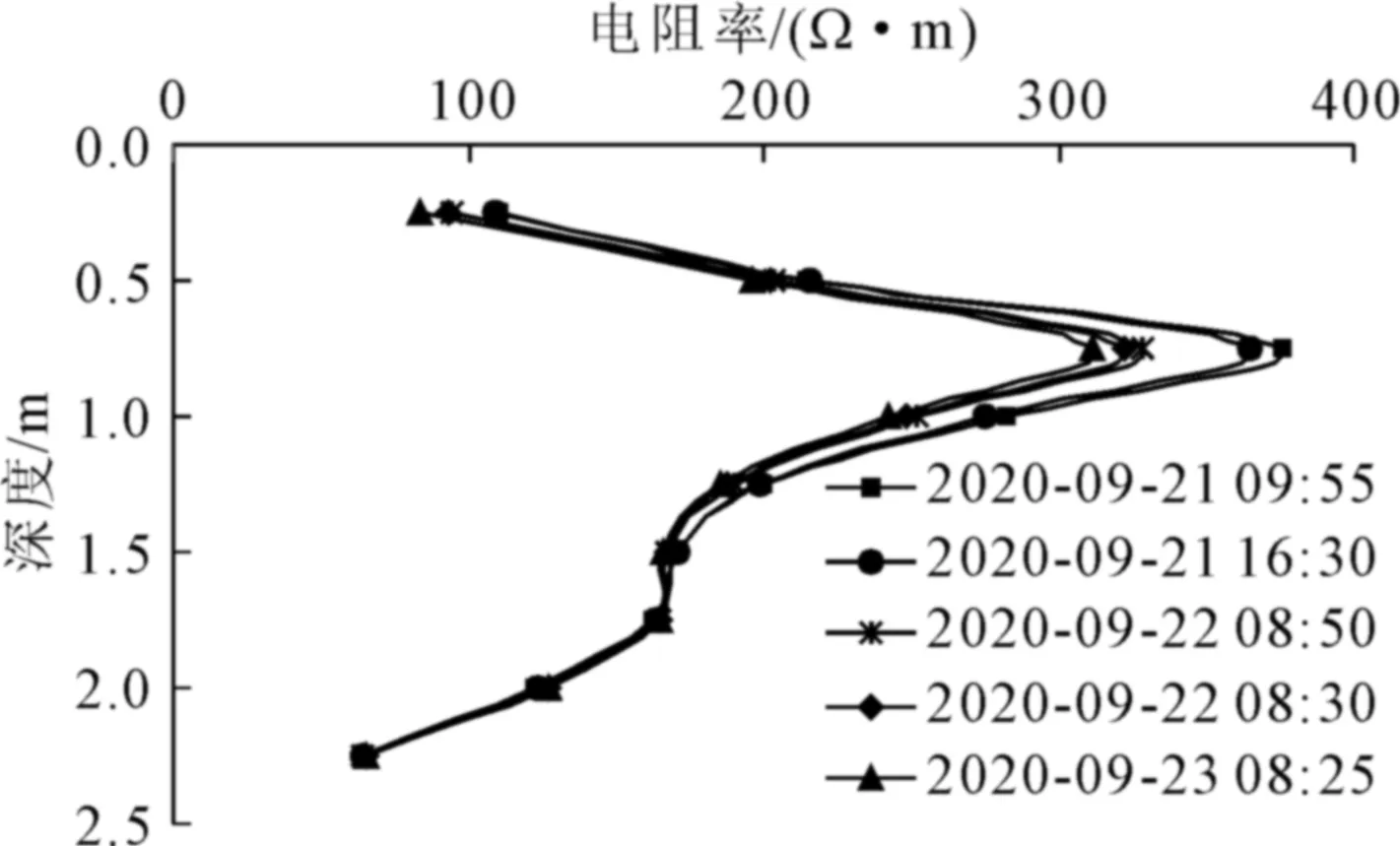
图4 电阻率随埋深变化图

与电阻率随深度变化不同，试验测得含水率随埋深先略微降增起伏后再一直降低,如图5所示。具体表现在在埋深0～0.2 m范围内含水率有下降趋势，0.2 m～0.3 m范围内增加，埋深大于0.3 m含水率下降的现象。此外，不同时间段埋深范围在0.10 m～0.45 m区间内含水率差值较大，含水率最大差值出现在埋深0.3 m处。且此埋深处含水率最大值达25.65%。

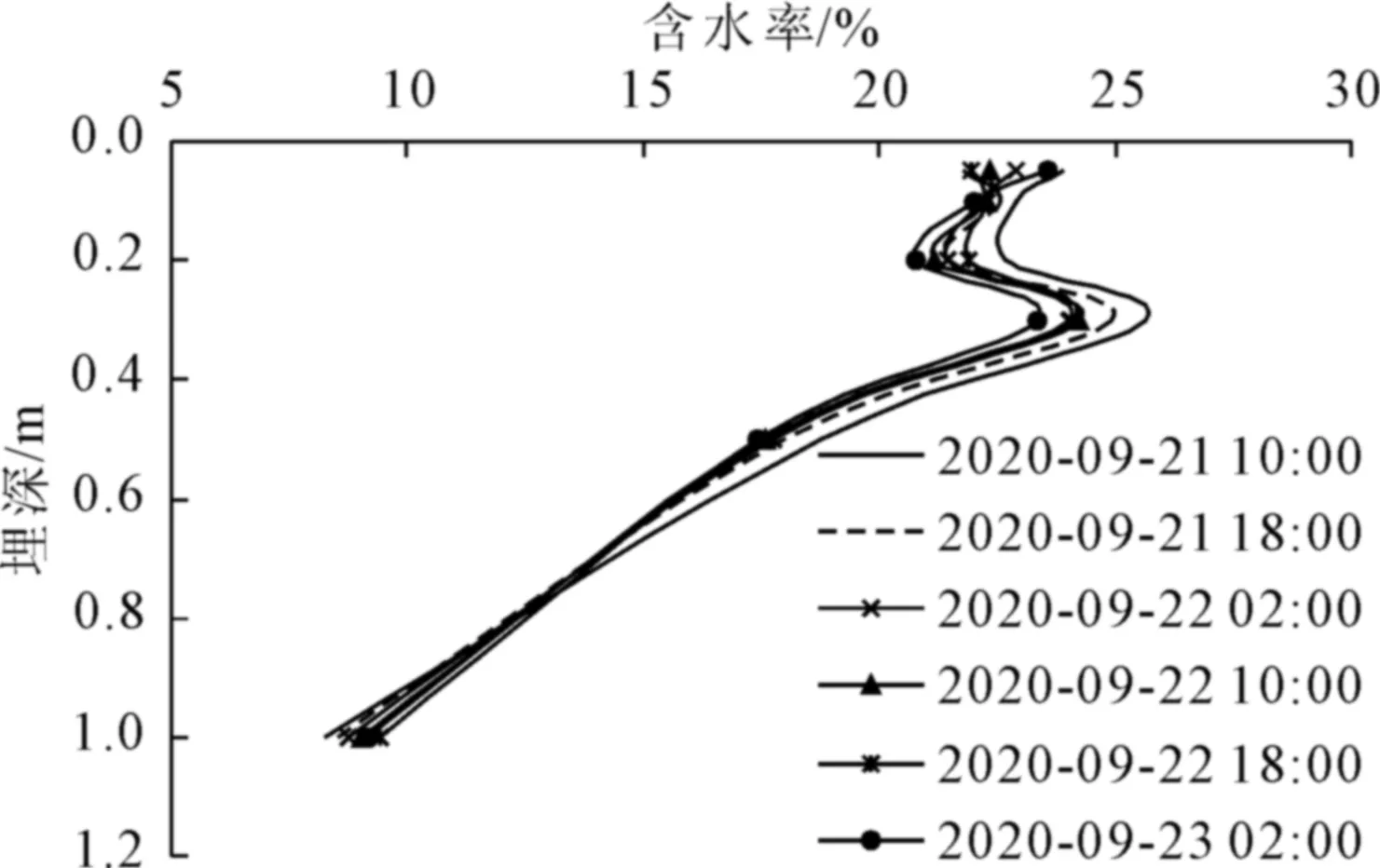
图5 含水率随埋深变化图

另外不同深度的水势随时间变化也有较大差异，见图6。埋深为0.1 m时，水势由最大值50 kPa随时间呈抛物线降低，直到30 kPa左右趋于稳定；当埋深为0.2 m时，水势在25 kPa附近总体呈上升趋势，变化幅度不大，相对比较平稳；当埋深为0.3 m时，水势由24 kPa先下降至22 kPa然后上升趋势，总体变化幅度也比较小。此外，上述结果还说明在测量剖面相对均匀、外界温差不大、孔隙水溶液成分相对单一的条件下，电阻率变化的主要外在因素是由水势的变化引起的，具体表现在9月22日之前水势相对较小，而电阻率值较大；9月22及以后水势增大，而电阻率相对减小，因而电阻率与水势二者变化趋势相反。

图6 水势随时间变化图

2.2 含水率与电阻率关系模型分析

为分析含水率与电阻率的关系，绘制剖面介质的含水率与电阻率的散点图于图7。基于所绘制的散点数据，拟合含水率与电阻率的不同数学关系模型汇总于表1。

图7 电阻率与含水率关系图

表1 电阻率与含水率关系模型分析结果

由于含水率与电阻率的负相关趋势，主要选取多项式函数、线性函数、对数函数3种类型的数学模型公式拟合两者的关系趋势，同时求出其相关系数见于表1，并根据实测数据绘制出含水率、深度、电阻率三者的关系模型见图8。

图8 电阻率、含水率与埋深关系图

如图7所示，3种数学形式模型的相关系数接近，均在0.87～0.92之间。由于线性模型极差相较于多项式和对数模型较小，因此初步选定多项式模型和对数模型进行分析。

为了更精确的确定拟合模型的形式并进一步分析其实用性，将根据观测点数据构建的模型代入剖面反演，并绘制图形于图9(多项式关系式)及图10(对数关系式)。

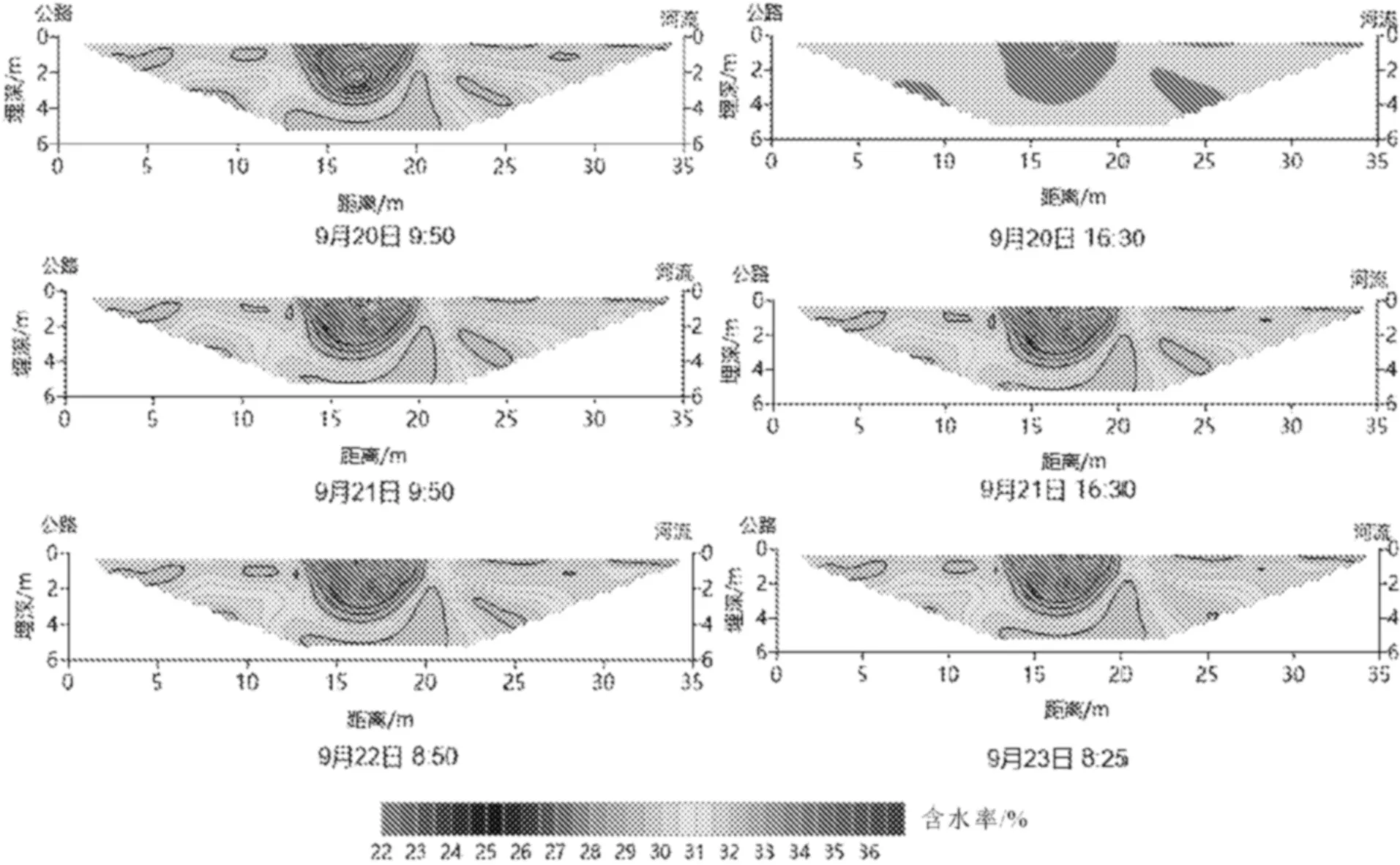
图9 多项式模型反演的剖面含水率分布图

图10 对数模型反演的剖面含水率分布图

对比分析图9和图10可知：电阻率差值变化最大的区域分布在入渗区域。试验开始之初，在渗水试验剖面中存在半圆形高阻区，经钻探发现，地下0～3 m范围内富含钙质结核，推测其为高阻区形成的原因。随着水分的入渗，该区域含水率升高，电阻率降低，相应高阻区范围减小。入渗试验结束，高阻区逐渐增加，电阻率相应增加。

由电阻率随埋深变化曲线可知，在埋深0.5 m～1.5 m范围内电阻率呈现峰值，随后在埋深1.5 m～2.0 m保持稳定后减小，说明在此范围内仍然有钙质结核的存在使其保持一定的电阻率。与之对应，含水率与埋深的曲线中，在埋深0～1 m范围内其总体趋势下降，因而，综合比对多项式和对数反演模型，得出对数模型基本能够反映水分入渗规律，而多项式模型反演结果与试验过程相差较大。因此，本文选择对数模型用来反演剖面含水率的变化过程。

3 结 论

对比不同时间段剖面介质的电阻率与含水率分布特征可以得出：

(1) 含水率与电阻率近似呈现负相关的关系，即当含水率增加时，电阻率减小。

(2) 电阻率与含水率随埋深的增大总体呈下降趋势，且埋深在0.75 m时电阻率达到最大值。

(3) 通过反演分析，推测在入渗区域范围内钙质结核是高阻区出现的原因，在此范围内含水率呈现降低趋势，电阻率相应出现峰值，进一步说明电阻率与含水率的负相关性，且对数模型能较为准确的反映试验过程水分入渗规律。