基于反函数原理的可控源大地电磁法全场域视电阻率定义

秦西社, 马劼, 郭文波,4, 戚志鹏,, 曹华科

(1.西北有色地矿集团，陕西 西安 710051; 2.长安大学 地质工程与测绘学院，陕西 西安710054; 3.中国地球物理学会 地球物理场多参数综合模拟重点实验室，陕西 西安 710054; 4.西安西北有色物化探总队有限公司，陕西 西安 710068)

0 引言

可控源大地电磁法(CSMT)是在大地电磁基础上发展起来的一种人工源电磁法[1],由于采用人工场源，克服了大地电磁天然源信号弱、信噪比低的缺点，使该方法在工程勘察、矿产资源勘查以及能源勘查等领域得到应用[2-7]。传统的可控源电磁法采用卡尼亚视电阻率进行数据解释，其效果直观，能够良好地反映地下的电性结构，在可控源电磁法解释中发挥了重要作用。但是，卡尼亚电阻率要求在远区进行测量，因为在过渡区进行测量会导致近区视电阻率公式与远区视电阻率公式的近似条件不成立，使计算的视电阻率存在畸变，这使得施工难度大大增加。针对这一问题，国内外许多学者提出了不同的校正方法和不同的视电阻率计算方法：曹昌祺[8]借鉴天然源大地电磁测深，通过CSMT理论曲线与实测曲线的对比，提出由比值法定义视电阻率，改进了波区视电阻率定义方法；Spies等[9]提出基于波阻抗的实部和虚部迭代计算视电阻率的简单方法；殷长春等[10]根据视电阻率定义基本原则，通过迭代从场值中用多项式逼近的方法直接求解视电阻率，并提出针对水平电偶源电场的全新的全区视电阻率定义方式和概念；方文藻等[11]将远区视电阻率乘以校正系数，简便快速地得到全区视电阻率；汤井田等[12-14]提出了求取阻抗实部等效电阻率和用电场定义视电阻率定义的方法，计算较为简便且能够较形象地反映地下介质信息；底青云等[15-17]提出了在近区和远区做近似的过渡区三角形法；毛先进等[18]提出水平电偶源的频率域电磁测深全区视电阻率直接算法；佟铁钢等[19]利用迭代法基于电场分量计算了可控源音频大地电磁全区视电阻率；韩自强等[20]利用二分法计算了电性双极性源全区视电阻定义。这些校正方法与全区视电阻率的提出使非远区的畸变得到很大的改善。近年来，何继善[21]提出了广域视电阻率计算方法，并逐渐发展为广域电磁法。广域电磁法在激发方面采用伪随机信号实现多个频率的同时发射与接收，在电阻率计算方面只测量电场或磁场的一个分量来计算全域视电阻率，可以在广大的测区范围进行观测。通过广域视电阻率定义，电磁测深的探测区域由远区推广到了中区，并有望实现近源探测[22]。

由均匀半空间偶极子频率域场各分量表达式可知，电磁场各分量的强度和波数有关，而波数包含了介质的电性参数。因此，CSMT的电磁场各分量与地层电阻率之间存在复杂的隐函数关系。在有效的测量范围内，每个电磁场分量必然存在一个电阻率值与之对应，这就为基于反函数思想用电磁场各分量定义全域视电阻率提供了基础。本文针对CSMT的广域视电阻率定义问题，从反函数原理出发，给出一种适合电磁场各分量的不受测区影响的全域视电阻率的定义方法，并对理论模型进行试验。

1 基于反函数原理的视电阻率计算方法

1.1 视电阻率计算方法

由于电磁场各分量均为地下介质电阻率以及场源的函数，因此将电磁场分量记为f(c,ρ,ω)，其中，c表示测点与场源的位置关系以及场源参数，ρ为大地电阻率，ω为发射源频率。为了利用反函数原理实现广域视电阻率的计算，将复杂函数f(c,ρ,ω)在ρ0的领域内进行泰勒展开：

f(c,ρ,ω)=f(c,ρ0,ω)+f′(c,ρ0,ω)·

(ρ-ρ0)+…+Rn(ρ) ，

(1)

当场值分量关于地下介质电阻率参数为单调函数时反函数存在，可将式(1)中高阶无穷小量忽略，得线性化函数：

f(c,ρ,ω)=f(c,ρ0,ω)+f′(c,ρ0,ω)(ρ-ρ0) 。

(2)

当反函数存在时，通过反函数原理，将式(2)改写成电阻率的函数，即可以获得迭代的视电阻率计算表达式：

(3)

式中：f(c,ρ,ω)为实测电磁场分量，f(c,ρ0,ω)为电阻率等于ρ0时均匀半空间模型的理论电磁场值，f′(c,ρ0,ω)为f(c,ρ0,ω)的一阶导数。可将式(3)改写为迭代格式：

(4)

1.2 均匀半空间频域电磁场与电阻率函数关系

根据均匀半空间电偶极子场表达式给出不同频率电磁场各分量随电阻率变化的曲线特征。图1所示为Ex电场分量模值、实部与虚部在不同频率关于电阻率变化的曲线；图2给出了Hy磁场分量模值、实部与虚部在不同频率关于电阻率变化的曲线；图3为Ex/Hy波阻抗分量模值、实部与虚部在不同频率关于电阻率变化的曲线。对于电场分量以及电场与磁场的比值随着电阻率变化呈单调函数，有利于基于反函数原理的视电阻率定义。对于磁场分量在电阻率变化过程中存在一个极值，可以在极值电阻率两侧分别采用反函数原理进行视电阻计算。

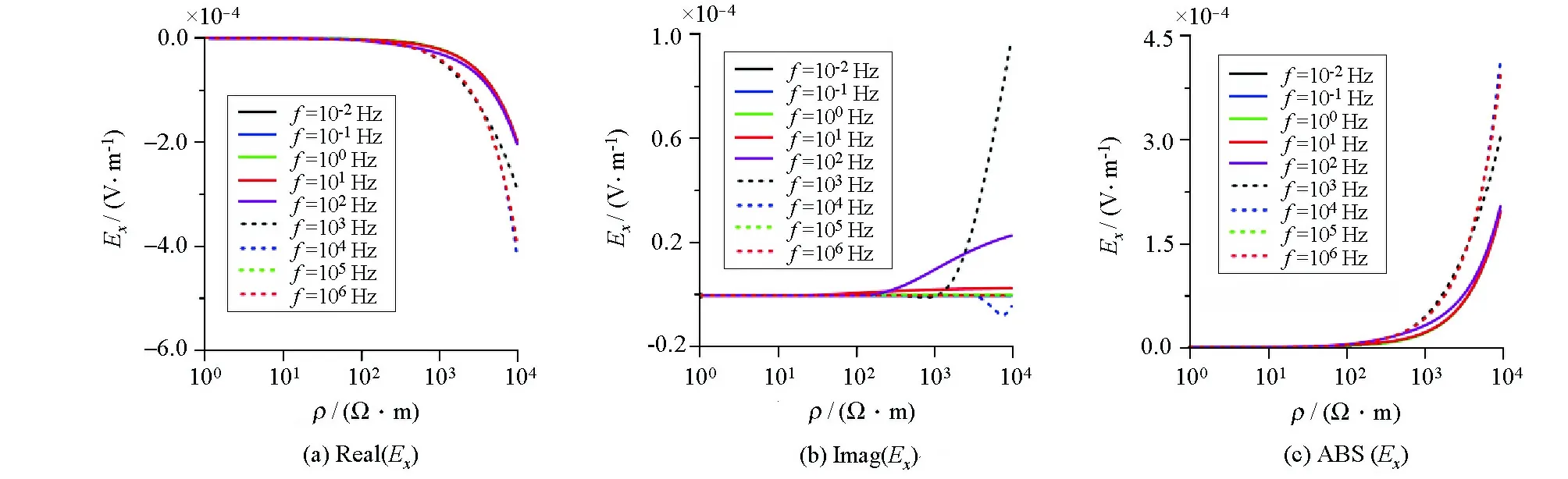
图1 频域电磁场Ex分量关于电阻率变换曲线特征Fig.1 Characteristic of Ex component in frequency domain about resistivity

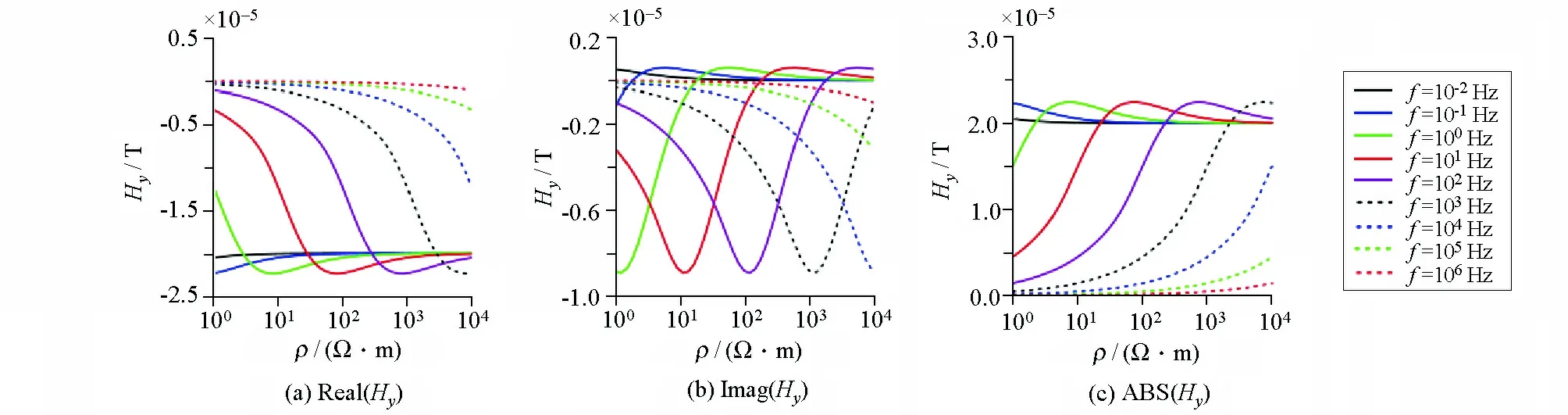
图2 频域电磁场Hy分量关于电阻率变换曲线特征Fig.2 Characteristic of Hy component in frequency domain about resistivity

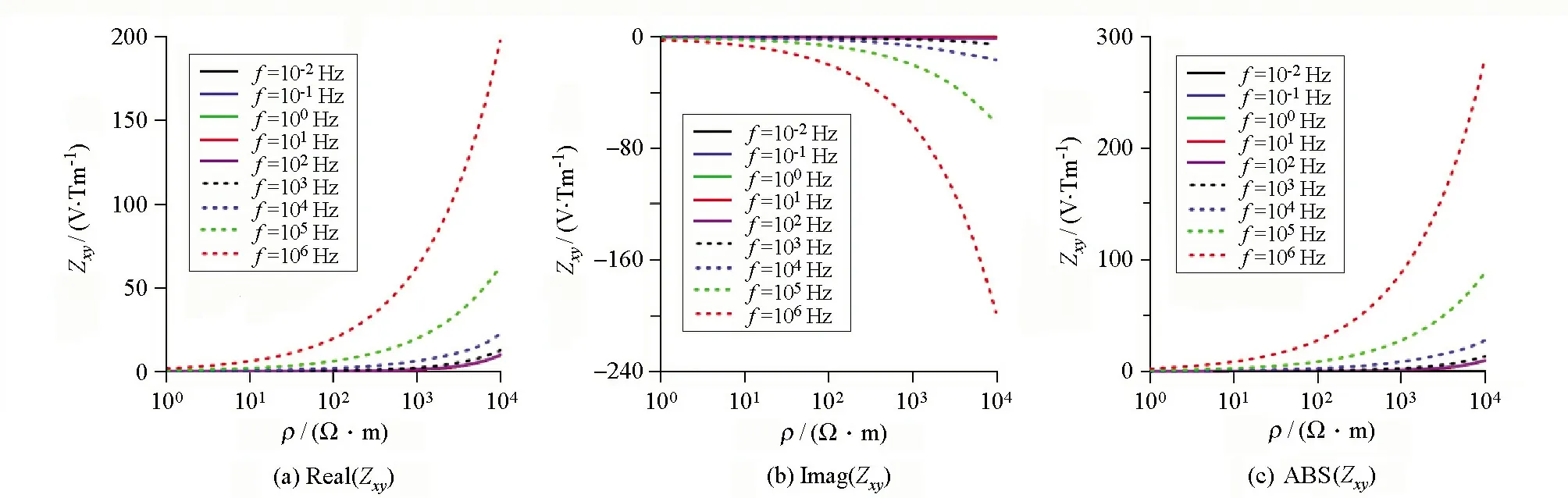
图3 频域电磁场Zxy分量关于电阻率变换曲线特征Fig.3 Characteristic of Zxy component in frequency domain about resistivity

已知均匀半空间电阻率值为ρ=20 Ω·m，分别采用卡尼亚视电阻率、基于反函数原理的视电阻率等计算模型视电阻率曲线；由图4可知卡尼亚视电阻率计算的视电阻率值随着偏移距增大，视电阻率的极大值逐渐减小，近场效应随偏移距的增大逐渐减弱。由图5可知，基于反函数原理定义的视电阻率不存在近场效应，不论在近区、过渡区、远区电阻率值均为ρ=20 Ω·m，与模型完全符合。

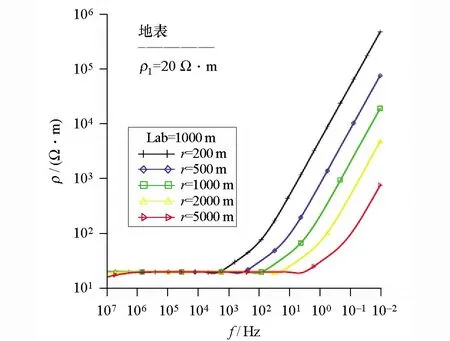
图4 基于卡尼亚视电阻计算的不同偏移距半空间视电阻率Fig.4 Different offset half-space apparent resistivitycalculations based on Cagniard apparent resistivity

图5 基于反函数原理的不同偏移距半空间视电阻率曲线Fig.5 Apparent resistivity for different offsets in half space based on the inverse function principle

2 层状模型分析

为验证文中视电阻计算方法，给定发射源参数：电流源长度1 000 m，电流1 A，偏移距分别为200、500、1 000、5 000 m；利用文中所述方法，分别用Ex、Hy、Ex/Hy、ABS(Ex/Hy)等分量来计算层状模型的视电阻率。

2.1 两层模型分析

设两层模型参数：第一层电阻率值ρ1=100 Ω·m，层厚h1=50 m；第二层电阻率为变化值,ρ2分别为2、3、5、8、20、30、50、80、200、300、500、800 Ω·m，构成D型和G型模型。基于反函数原理定义的视电阻率计算结果见图6～图8。

将图6～图8进行对比分析，发现曲线首支总趋于第一层电阻率，尾支总能表征第二层电阻率值相对于第一层电阻率变化趋势。在收发距较小的情况下，受收发装置所限，曲线尾支不能趋近于最后一层电阻率，这是因为当收发距较小时，电磁场与频率无关，等效为几何测深装置，因此最后一层电阻率趋于常值。在收发距较大的情况下，曲线尾支逐渐趋近于最后一层电阻率。

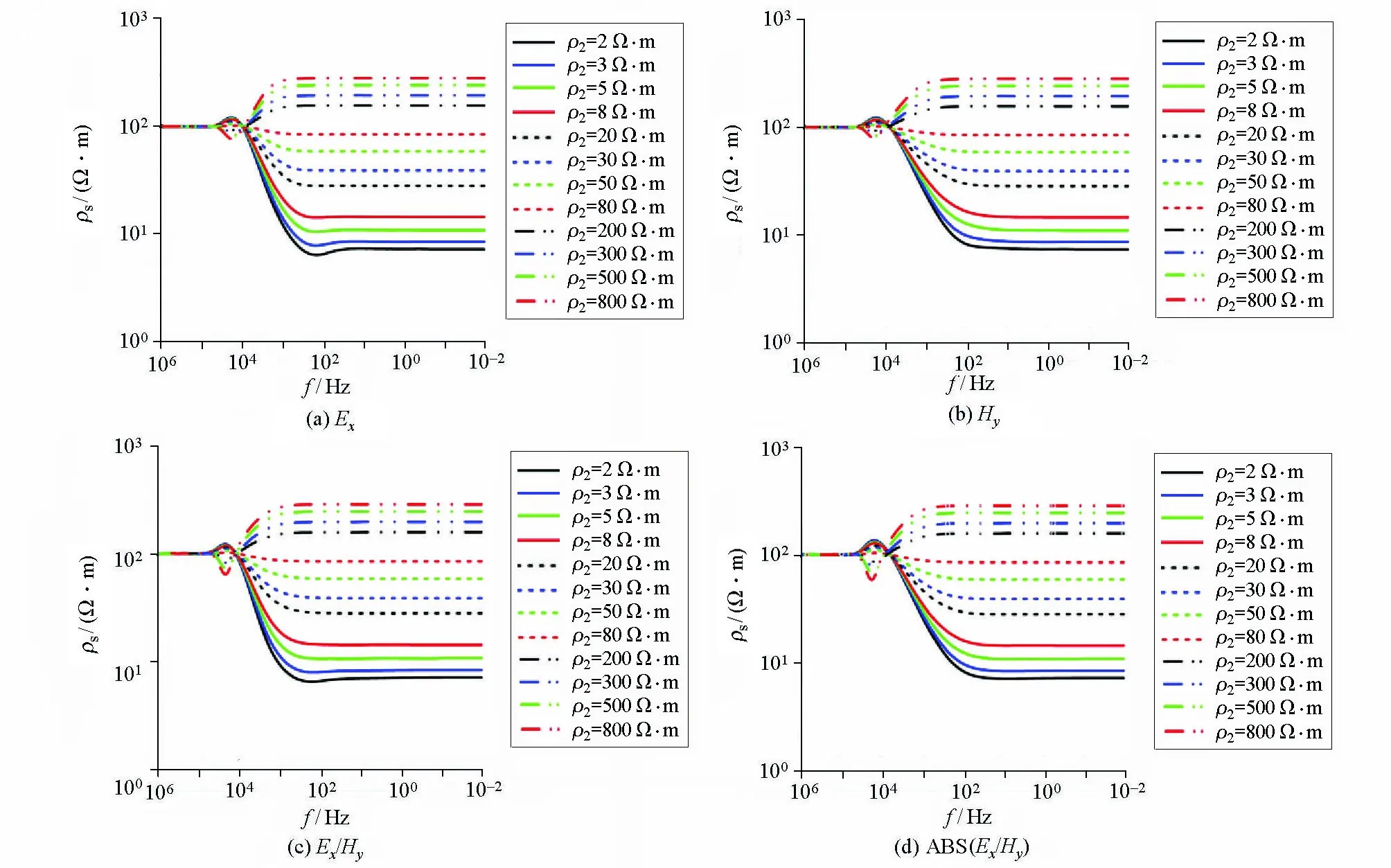
图6 偏移距200 m时两层模型各分量定义的视电阻率特征Fig.6 The apparent resistivity characteristics defined by each component of the two-layer model when the offset is 200 meters

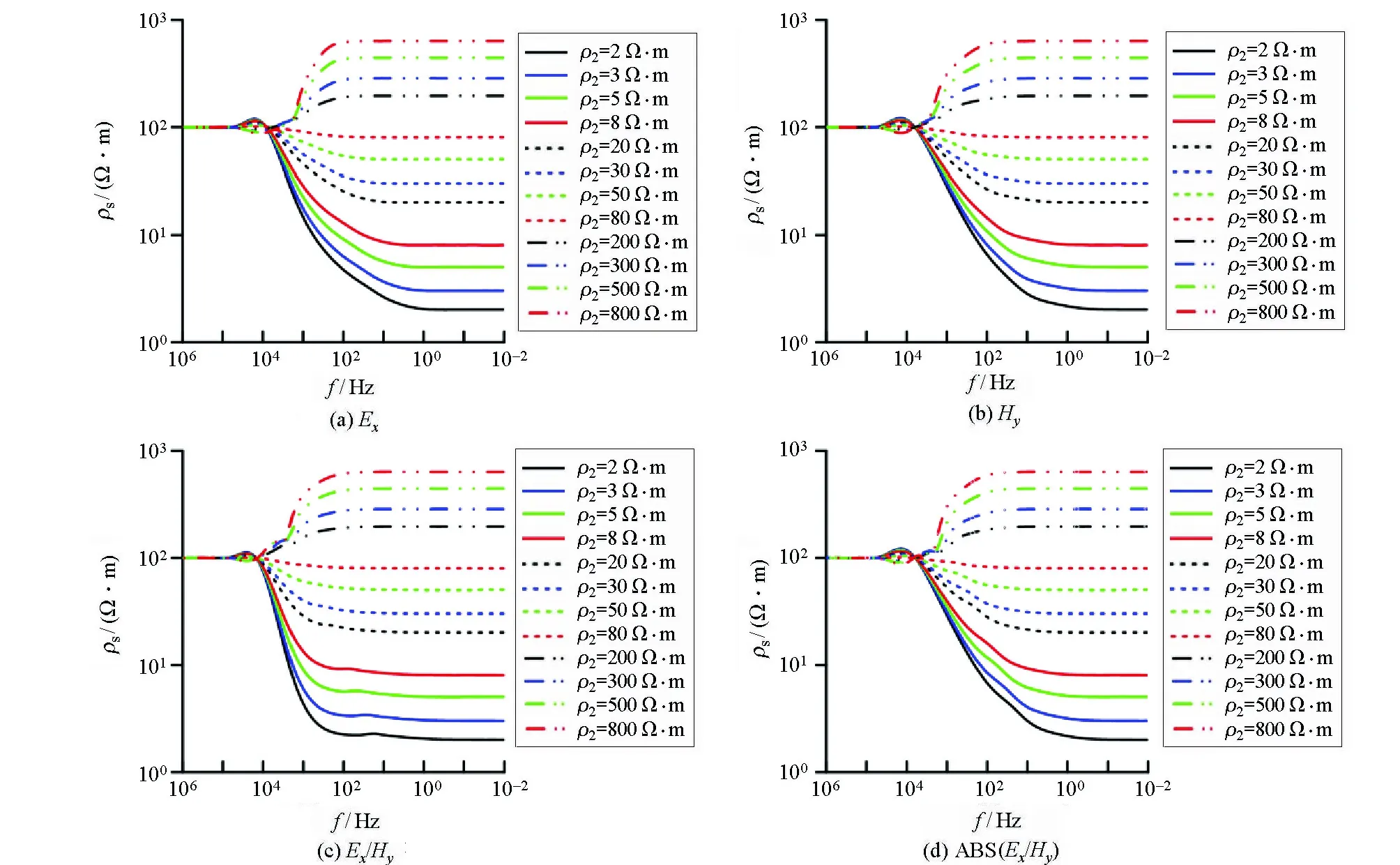
图7 偏移距1 000 m时两层模型各分量定义的视电阻率特征Fig.7 The apparent resistivity characteristics defined by each component of the two-layer model when the offset is 1 000 meters

图8 偏移距5 000 m时两层模型各分量定义的视电阻率特征Fig.8 The apparent resistivity characteristics defined by each component of the two-layer model when the offset is 5 000 meters

整体上看，无论是D型还是G型，其视电阻率计算结果在高频段和低频段都能很好地反映模型的电阻率，曲线光滑，且较真实地反映了地电结构。

2.2 三层模型分析

2.2.1 改变中间层电阻率

设三层H型模型参数：第一层电阻率ρ1=100 Ω·m，层厚h1=10 m；第二层电阻率为变化值，ρ2分别为10、20、30、50、80 Ω·m，h2=30 m；第三层电阻率ρ3=100 Ω·m。基于反函数原理的视电阻率定义结果见图9～11。

由图9～11可见：在收发距较大情况下，高频段和低频段的视电阻率与模型电阻率一致；由于中间层为低阻，所以全域视电阻率曲线表现为下凹形态，这与所设计的正演模型吻合。总体来说，CSMT的全域视电阻率定义能细致刻画地电信息的变化，在不同的偏移距处可以准确定义，进一步说明CSMT全域视电阻率定义方法的准确性。

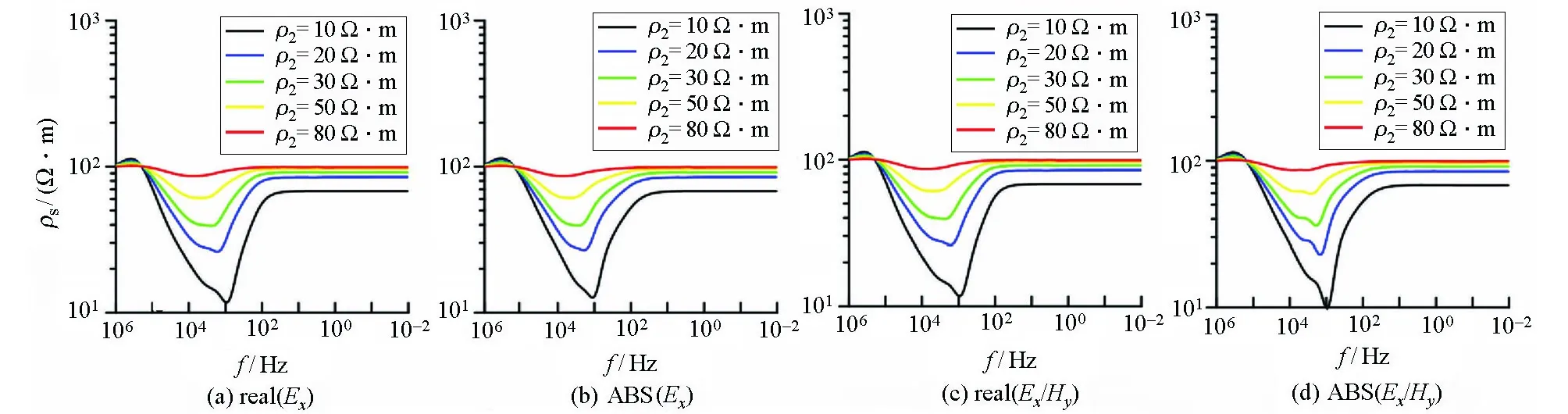
图9 偏移距500 m时H型模型各分量定义的视电阻率特征Fig.9 The apparent resistivity characteristics defined by each component of the H-type model when the offset is 500 meters

图10 偏移距1 000 m时H型模型各分量定义的视电阻率特征Fig.10 The apparent resistivity characteristics defined by each component of the H-type model when the offset is 1 000 meters

图11 偏移距5 000 m时H型模型各分量定义的视电阻率特征Fig.11 The apparent resistivity characteristics defined by each component of the H-type model when the offset is 5 000 meters

设三层K型模型参数：ρ1=10 Ω·m,h1=10 m;第二层电阻率为变化值，ρ2分别为15、20、30、50、80 Ω·m，h2=30 m;ρ3=10 Ω·m。基于反函数思想定义的视电阻率结果见图12～14。

对比图12～14可知，当偏移距较小时视电阻率尾支趋于定值，随着偏移距的增加电阻率曲线尾支能够较好地趋近于底层电阻率。总体而言，视电阻率曲线能较好地拟合给定模型参数，中间夹层为高阻层时，视电阻率曲线存在上凸，能够反映中间高阻层，并且随着电阻率的增加异常逐渐变大，较好地反映了模型的电阻率特征。

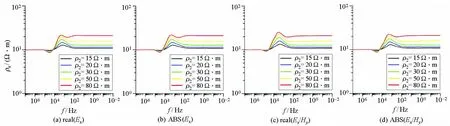
图12 偏移距200 m时K型模型各分量定义的视电阻率特征Fig.12 The apparent resistivity characteristics defined by each component of the K-type model when the offset is 200 meters

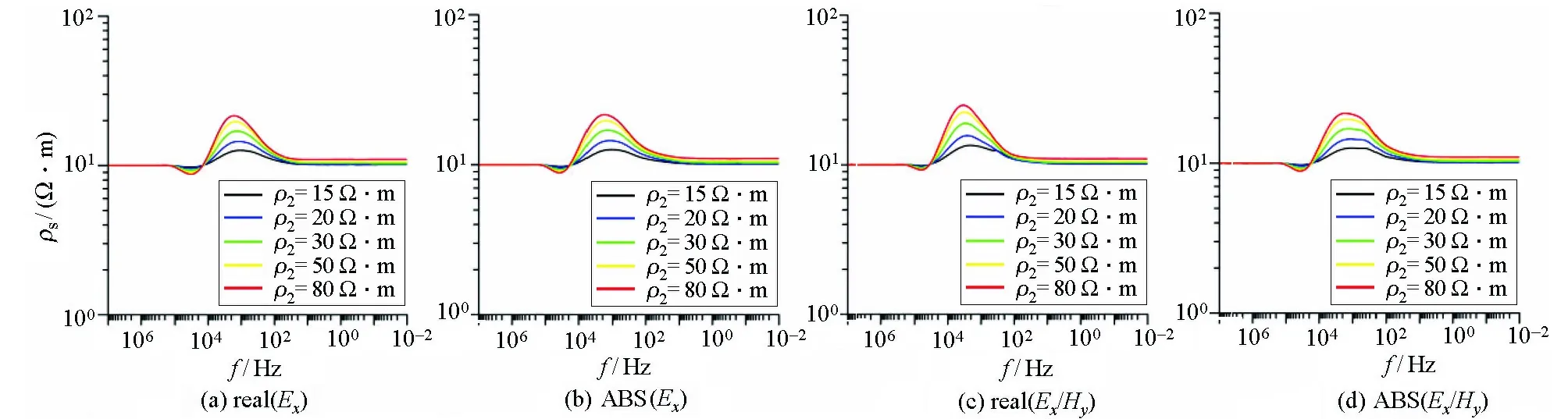
图13 偏移距500 m时K型模型各分量定义的视电阻率特征Fig.13 The apparent resistivity characteristics defined by each component of the K-type modelwhen the offset is 500 meters

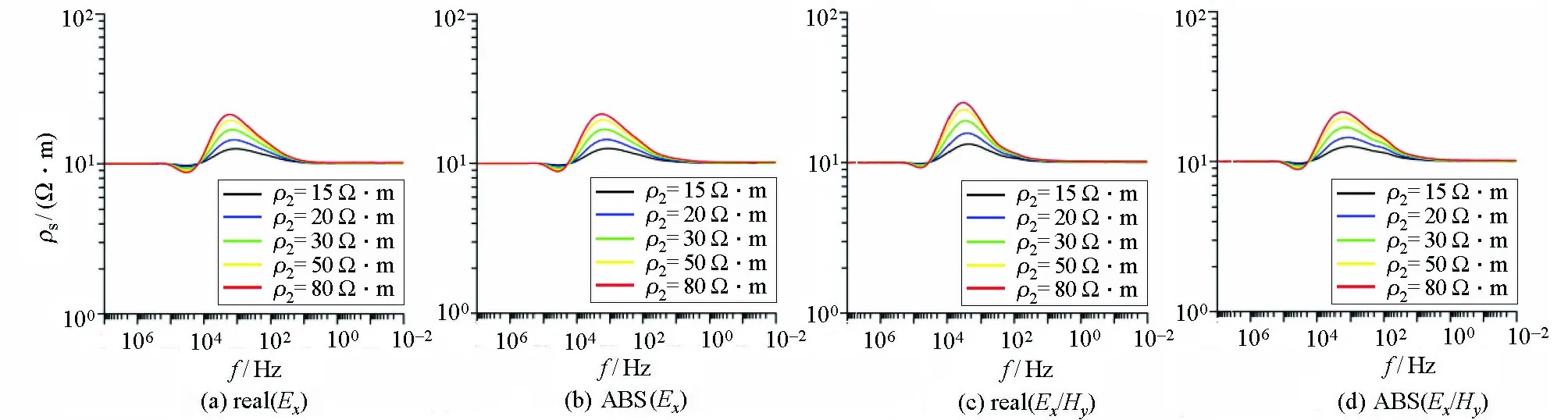
图14 偏移距1 000 m时K型模型各分量定义的视电阻率特征Fig.14 The apparent resistivity characteristics defined by each component of the K-type modelwhen the offset is 1 000 meters

2.2.2 改变中间层厚度

改变三层模型的中间层厚度。H型模型：ρ1=100 Ω·m，h1=10 m；ρ2=10 Ω·m，h2分别为5、10、15、30、50、80 m；ρ3=100 Ω·m。基于反函数原理的视电阻率定义结果见图15。K型模型：ρ1=10 Ω·m，h1=10 m；ρ2=20 Ω·m，h2分别为5、10、20、30、50、80 m；ρ3=10 Ω·m。基于反函数原理的视电阻率定义结果见图16。

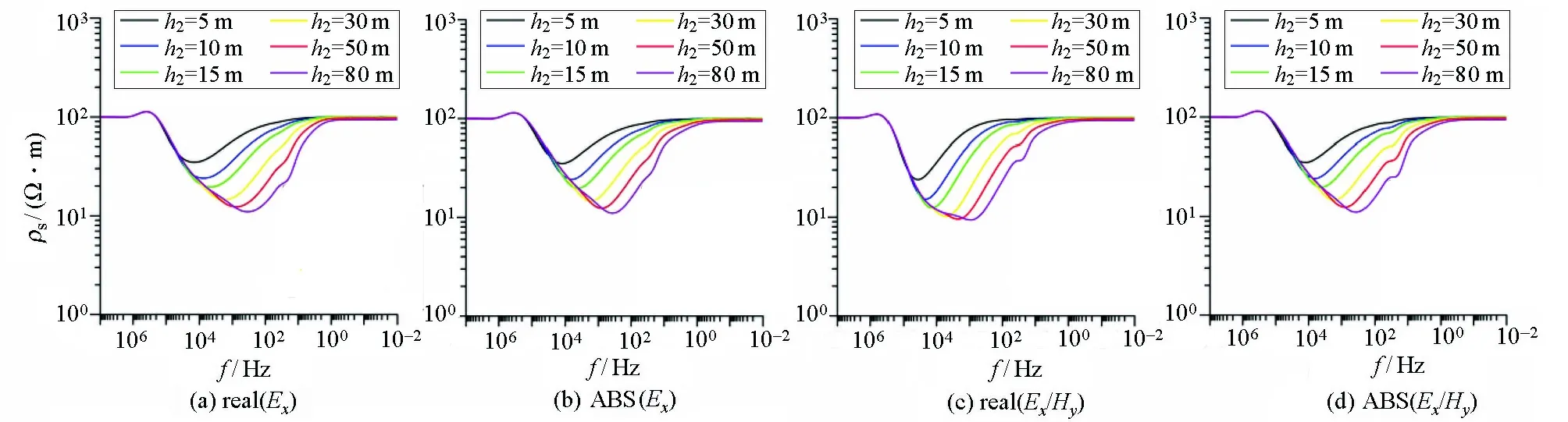
图15 层厚改变时H型模型各分量定义的视电阻率特征Fig.15 The apparent resistivity characteristics defined by each component of the H-type model with layer thickness changes

图16 层厚改变时K型模型各分量定义的视电阻率特征Fig.16 The apparent resistivity characteristics defined by each component of the K-type model with layer thickness changes

对于H型和K型模型，由图可见：在地层厚度较小时中间层的电阻率异常较小，在层厚逐渐增大的情况下，异常范围逐渐增大，曲线缓慢趋于平稳，视电阻率曲线的“下凹”与“上凸”更加明显；各分量定义的视电阻率都能对模型有较好的反映。

3 结论

基于反函数定理实现了任意分量的CSMT全区视电阻率定义，均匀半空间下层状模型的视电阻率计算结果充分说明了本文算法的有效性。本算法可以实现各种地电模型全区全频段的视电阻率计算，相对于卡尼亚视电阻率，曲线形态没有畸变，能正确反映地下电性结构，且计算速度快、精度高。实际工作中，可根据测量的单分量或多分量数据来计算视电阻率，方便快捷地实现对野外资料数据的处理。

分析了偏移距、中间层厚度以及中间层电阻率等参数对视电阻率计算的影响。野外应避免收发距相对为极小量，因为这时电磁场与频率无关，装置等效为几何测深，磁场与电阻率无关而低频电场分量计算的视电阻率趋于常值，不能真实反映地层电阻率。在不同偏移距测区，从各分量的视电阻率曲线图可以看到，视电阻率曲线的首支都能够很好地反映第一层的真实电阻率，在尾支也能不断趋于最后一层的真实电阻率，三层模型的曲线变化光滑且能较好地反映中间层的变化趋势，都能很好地逼近模型电阻率。