带约束的多辐射场源半航空瞬变电磁一维自适应正则化反演方法

张 莹 莹

(新疆大学 地质与矿业工程学院，新疆 乌鲁木齐 830047)

0 引言

半航空瞬变电磁法(semi-airborne transient electromagnetic method, semi-airborne TEM)，也称为地空瞬变电磁法，采用地面发射、空中接收的工作方式，兼具地面发射功率强、勘探深度大和空中接收面积测量、工作效率高的双重优点，目前已在地热调查、火山结构调查、地下巷道调查、地下水盐渍化及地下水监测、采空区探测、隧道勘察、古河道结构探测等领域得到成功应用[1-11]。半航空TEM的快速发展集中在近十年，目前对半航空TEM的研究仍处在初步阶段，数据处理和解释大都仍基于一维解释方法[12]，研究内容主要集中在视电阻率求解、快速成像方面，如：阳贵红分析了接收高度对电磁响应的影响并设计了求解全区视电阻率的算法[13]；嵇艳鞠等基于三层BP神经网络和Levenberg-Marquardt算法实现了电性源半航空TEM神经网络视电阻率反演[14]；张莹莹等对多分量磁场响应和磁场的时间导数响应进行分析并基于反函数原理实现了多分量的全域视电阻率定义[15]；吴启龙研究了半航空TEM视电阻率成像，并将该算法应用于复杂地形地区隧道勘察[10]；李貅、张莹莹等基于瞬变电磁拟地震成像技术提出了地空瞬变电磁法逆合成孔径成像，并基于浮动薄板原理研究了地空TEM快速成像算法[16-17]；吕仁斌利用查询表方式求解视电阻率，并结合视深度公式研究了电导率深度成像[18]；王仕兴等基于分段二分搜索算法建立起电导—电磁响应数据库，实现半航空TEM电导率深度快速成像[19]。这类研究的特点是计算速度快，不依赖初始模型，但其解释结果大都很难提供与层厚相关的信息，且精度普遍较低，因此，诸如视电阻率计算和快速成像方法多用作定性分析。在一维反演方面，已有部分国内外学者做了相关工作，如：张澎等引入并行技术实现了最平缓模型约束条件下的半航空时间域电磁数据自适应正则化反演算法[20]；Abdallah等将频率域电磁反演方法用于GREATEM的时间域数据，该法适用于对电阻率横向变化大的数据进行反演[21]；赵涵等以Occam反演理论为基础研究了多辐射场源地空瞬变电磁一维反演算法[22]；杨聪等结合自适应正则化反演方法和阻尼最小二乘反演方法提出自适应正则化—阻尼最小二乘反演算法，该法可在一定程度上提高半航空TEM对高阻的分辨率，提高反演精度[23]。目前已经发表的一维反演方面的研究成果大都基于单个辐射源，实际上半航空TEM的辐射源可以是单一的，也可以是多个，磁性源也可视作多个辐射场源的叠加。多辐射场源能够减少单个辐射源体积效应的影响，在地下多方位激发地质体，获得多方位耦合信息,可通过调整电性源的位置或电流方向，有针对性地加强某一分量的采集信号强度，削弱随机噪声，提高半航空TEM对异常体的分辨能力[15,24]。在地形复杂地区，半航空TEM具有重要优势，若再结合多辐射场源技术，对于实现高分辨率深部探测具有重要意义。与航空电磁法类似，半航空TEM同样面临数据量大、数据信噪比低等问题，可以借鉴航空电磁资料反演中综合各种先验约束信息并辅以适当的最优化的正则化反演方法，降低反演多解性，实现半航空TEM数据稳定快速的一维反演[25]。

本文结合半航空TEM的研究现状和具体特点，以多辐射场源半航空TEM为例，实现了垂直分量带约束的自适应Occam反演算法，在Occam反演的基础上[26]，采用陈小斌等提出的CMD自适应调节方案改进了拉格朗日乘子的处理方式[27]，省去传统Occam反演中搜索拉格朗日乘子的大量计算过程，并利用自然边界条件和模型修正量可行下降方向法对反演过程进行约束，减少反演过程的计算量，保证反演过程的稳定性和计算效率。典型层状地电模型反演结果表明，该法可以通过较少的迭代次数获得可靠的、抗干扰能力强的反演结果，为实现多辐射场源半航空TEM数据稳定快速一维反演打下理论基础。

1 多辐射场源TEM一维正演方法

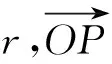
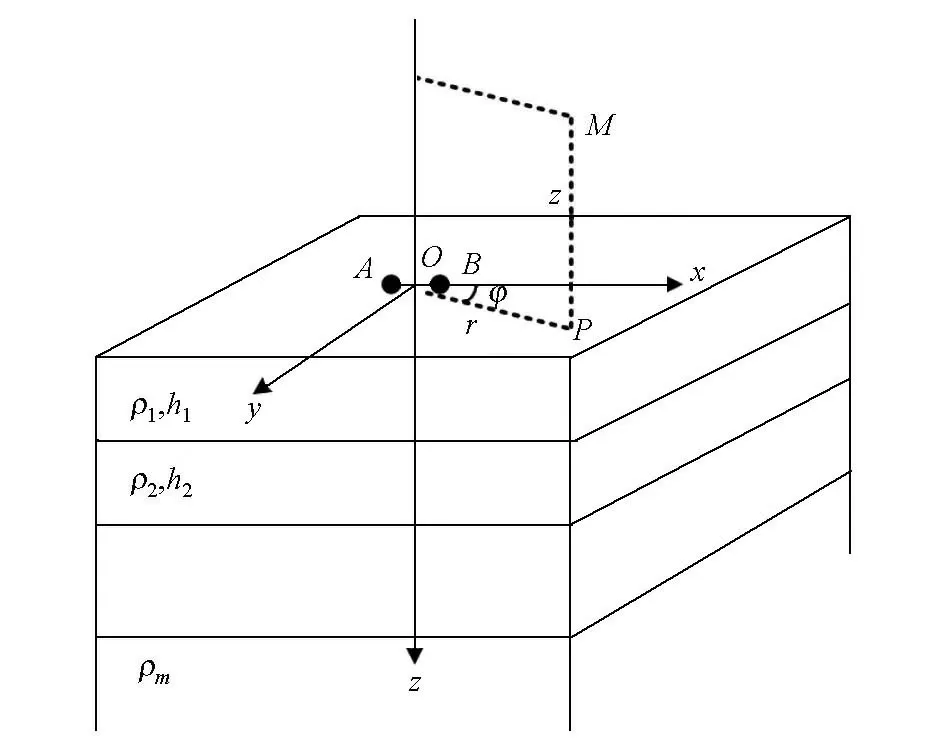
图1 地表电偶极子层状模型示意Fig.1 Schematic diagram of an electric dipole on the surface of layered earth

(1)

根据电矢量位与磁感应强度的对应关系：

(2)

可得层状大地地表电偶极子在空中产生的频率域垂直分量磁感应强度表达式：

(3)

(4)

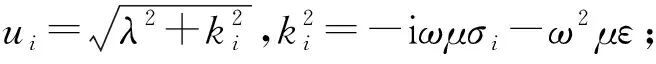
考虑到实际工作中使用的发射源可能长达数千米，在近区和过渡区，场源不能被看作电偶极子，本文采用剖分叠加、有限求和的方式，将发射源剖分成多段电偶极子，然后将每一段电偶极子产生的频率域磁场叠加在一起近似计算总场源的频率域响应。对于每一段剖分的电偶极子，z轴始终指向下，选定一个电性源所在的坐标系作为标准坐标系(如图2中的发射源1)，可得层状大地多辐射场源在空中产生的频率域垂直分量磁感应强度表达式[28]：

图2 多辐射场源剖分示意Fig.2 Coordinate sketch of multi-source subdivision

(5)

式中：PEij=Iidsij，Ii表示第i个电性源的供电电流，dsij表示第i个电性源剖分的第j个电偶极子的长度；φij和rij分别表示测点M在地表的投影P与第i个电性源剖分的第j个电偶极子的夹角和对应的偏移距；n为电性源总个；mi为第i个电性源的剖分段数。

当采用阶跃电流作为发射波形时，时间域响应可以由频率域响应通过正弦变换得到：

(6)

2 多辐射场源瞬变电磁一维反演方法

2.1 Occam反演方法

Occam反演是一种改进的带平滑约束的最小二乘反演方法，在反演时要求实测数据与模型数据的拟合误差在一定条件下达到极小，同时也要求反演模型的粗糙度达到极小，反演的目标函数为[26]：

(7)

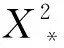
R=‖∂m‖2；

(8)

其中∂为粗糙度矩阵，形式如下:

(9)

在初始模型m1附近作线性化，将非线性问题转为线性，则：

F[m1+Δ]=F[m1]+J1Δ。

(10)

式中：Δ是模型修正量；m1是反演一次迭代的解；J1是初始模型的偏导数矩阵，即雅克比矩阵，其元素

Jij=∂Fi[m]/∂mj，

(11)

mk+1={μ∂T∂+(WJ[mk])TWJ[mk]}-1·

{WJ[mk]}TWdk，

(12)

其中：

dk=d-F[mk]+J[mk]mk。

(13)

反演拟合误差为实测数据和响应数据的全域视电阻率均方根相对误差：

(14)

反演终止标准为上述均方根相对误差小于给定值。

2.2 拉格朗日乘子调节方案

根据式(7)，拉格朗日乘子的大小决定了反演的主要拟合对象。在反演中，反演效率、反演矩阵的病态程度和反演模型收敛性都与拉格朗日乘子有关。经典的求取最佳拉格朗日乘子的方法是一维线性搜索，但该法每次迭代需要多次正演和求解反演方程，导致计算量很大；且每次迭代可能存在多个解，选取不当可能导致反演不收敛。本文采用陈小斌等提出的CMD自适应调节方案[27]，该方案在满足总目标函数极小的同时，还能近似满足数据目标函数极小和模型约束目标函数极小的条件：

(15)

式中Δdk是第k次实测数据与模型数据的残差。该方案不需要额外的正演计算，调解方案简单，可以有效减少计算量。

2.3 可行下降方向法约束

反演方程式(12)求解的是一个数学问题，为了尽量减少多解性的影响，引入可行下降方向法[29]。但反演过程中每次迭代的结果并不总是满足自然规律，可能是极大值、极小值或负数，这与实际地质情况显然不符。为此，设定m下和m上分别为mk的下界和上界，即可行域，对每一次迭代的结果mk进行约束，判断每一层反演的电阻率是否超出给定的下界m下和上界m上，文中取m下=0.1 Ω·m，m上=1 000 Ω·m。若超出可行域，即不满足自然边界条件，给出如下可行下降方向法：

1) 对于可行域内的mk，利用式(13)求出mk+1，计算出模型修正量Δmk=mk+1-mk。

2) 令

(16)

其中ε为给定的小正数。

3) 令

(17)

这样求得的mk+1必在可行域内。反演要达到更高的精度，要求相应足够小的步长才有可能收敛，否则，在接近极小点附近时，模型修正量大，可能使反演结果快速陷入局部极小，导致迭代在不能满足精度要求后进入发散轨迹。在此建议模型修正量的最大值在50 Ω·m以内。

这首诗暗用林和靖梅妻鹤子的典故，但不直白，颇含蓄蕴藉，耐人寻味。他将长安二月未见梅的原因诙谐地归结于梅花还在等她的主人到来。董玘的七律也有个别写得形象而富有哲理，如《题画》：

2.4 雅可比矩阵优化

由式(12)可知反演迭代的主要工作量在于雅克比矩阵的计算，若使用传统的差分方法计算雅克比矩阵的矩阵元，若有N个反演参数就必须进行N次正演，相应的反演时间基本上就是正演耗时的N+1倍。瞬变电磁测深Occam反演的地层参数包括几何参数和电参数，一般同时待反演的参数能达到几十个，这就导致雅克比矩阵的计算量很大，因此研究雅克比矩阵的快速算法对于瞬变电磁资料反演具有重要意义。在此，借鉴文献[30]中的方法对灵敏度矩阵进行更新，减少雅可比矩阵的计算量：

(18)

3 层状模型算例

为检验上述反演算法的可靠性，对层状模型的一维正演数据进行反演。多辐射场源采用与电流方向相反的平行源，装置布置示意见图3，电性源长度均为200 m，间隔200 m，发射电流为阶跃脉冲，电流大小10 A，电流方向如图中箭头所示，在off-time取了20个时间道电磁响应作为反演数据，接收线圈接收面积1 m2，匝数1，飞行高度100 m，以坐标原点O(0,0)为例进行分析。反演过程中，设置最大迭代次数20次，反演地层30层，首层厚度为5 m，层厚按对数等间隔进行离散，反演的初始模型均为电阻率100 Ω·m的均匀半空间。

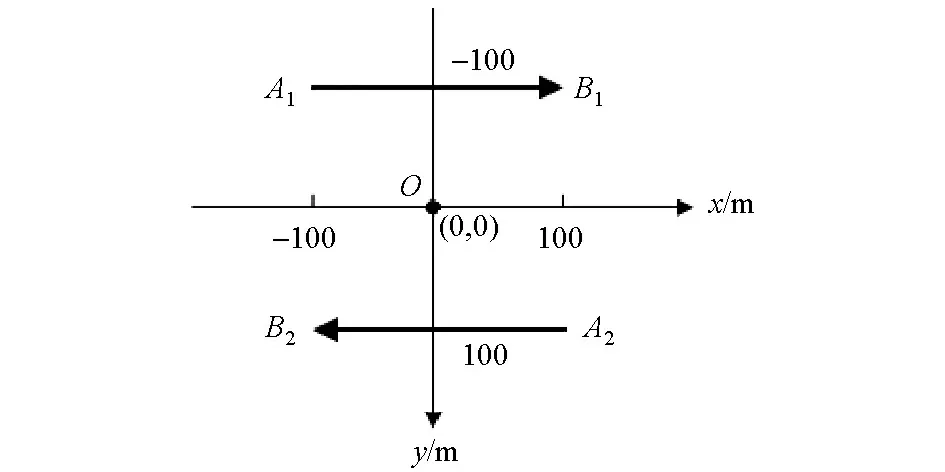
图3 平行源装置布置Fig.3 Arrangement diagram of parallel source device

3.1 三层模型

选择三层模型中典型的H和K型地电模型进行反演试算，H型模型各层电阻率分别为100、10、100 Ω·m，层厚为200、100 m；K型模型各层电阻率分别为100、1 000、100 Ω·m，层厚为200、100 m。图4所示是H型模型反演结果，图中显示随着反演迭代次数增加，拉格朗日乘子和拟合误差快速下降，反演算法快速稳定收敛，反演结果逐渐逼近真实模型，最终反演得出的各地层的深度和电阻率均与真实模型吻合较好。通过10次反演迭代，拟合均方根相对误差降至约1%，已能获得较为理想的反演结果。

图4 H型模型反演结果Fig.4 Inversion results of H model

图5所示是K型模型反演结果。图中显示随着反演迭代次数的增加，拉格朗日乘子、拟合误差、反演结果均表现出与H型模型相似的变化趋势，反演结果基本能反映出真实模型的特征。所不同的是，由于浅部低阻层的屏蔽作用，最终反演结果中间高阻层的电阻率值无法反演出真实模型的电阻率值，这也与瞬变电磁法对高阻层不够灵敏的特点相吻合。

图5 K型模型反演结果Fig.5 Inversion results of K model

3.2 四层模型

设计了更为复杂的四层HK模型对反演算法进行验证。HK型模型各层电阻率分别为200、50、300、100 Ω·m，层厚为100、100、100 m。随着反演迭代次数的增加，拉格朗日乘子、拟合误差、反演结果表现出与H型和K型模型相似的变化趋势，反演过程快速稳定，最终能够得到与真实模型特征吻合的反演结果。图6显示，本方法对第二层(低阻层)的反演效果很好，与真实模型很接近，但对高阻层没有准确反演出真电阻率值；随着迭代次数增加，拉格朗日乘子逐渐减小，数据拟合误差逐渐减小，最后趋近于0.4%，经过10次迭代，本文算法已经可以获得较好的反演结果。

图6 HK型模型反演结果Fig.6 Inversion results of HK model

4 含噪数据算例

在野外实际工作中，由于各种噪声源掺杂，半航空瞬变电磁测量的数据包含各种噪声，如随机噪声和相关噪声。为了评价噪声对上述反演算法的影响，按文献[25]的方法对一维正演所得的瞬变电磁响应添加高斯噪声模拟含噪数据进行一维反演，t时刻一维正演瞬变响应数据中加入如下所示高斯随机噪声：

(19)

式中：cnoise为常数，表示噪声大小；tNd和VNd分别表示最后一个(第Nd个)延时及该时刻的理论瞬变响应值。这种噪声表现为晚期信号信噪比低的特征，与实际情况相符。

4.1 三层模型

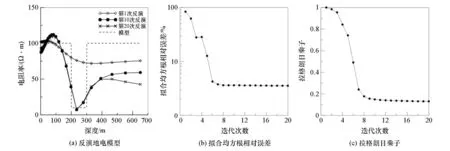
图7 cnoise=0.3高斯随机噪声H型模型反演结果 Fig.7 Inversion results of H model with cnoise=0.3 Gaussian noise

图8所示为添加cnoise=0.3高斯噪声的K型模型反演结果，由于电磁场对高阻的不敏感性，对中间高阻层的反演结果一般，不能准确刻画高阻层电阻率值。随着迭代次数的增加，拉格朗日乘子逐渐降低，但受噪声影响，拟合均方根相对误差在迭代8次时就逐渐趋于稳定。对比图5a和图8a可见，噪声对该模型反演结果的影响同样主要体现在深部，对应模型深度大于500 m的反演结果。

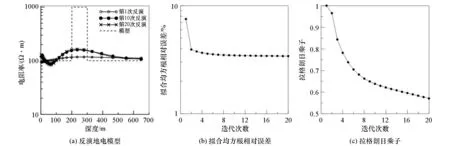
图8 cnoise=0.3高斯随机噪声K型模型反演结果Fig.8 Inversion results of K model with cnoise=0.3 Gaussian noise

4.2 四层模型

为了分析噪声强弱对反演结果的影响，采用前文中的HK型四层模型，在一维正演瞬变响应中分别加入cnoise=0.1、0.3的高斯随机噪声，利用本文提出的方法对地下电阻率进行反演。图9所示为含cnoise=0.1高斯噪声的反演结果。对比图6a和图9a可以看出，由于噪声信号强度较弱，含噪与不含噪数据的反演结果差别不大，能够较好地刻画出地下电阻率变化趋势，对于浅部低阻层反演效果较好，层界面位置也较为清楚，但是对于较深的高阻层反演效果一般，没有准确反演出真电阻率值，仅反映出在相应层位存在高阻层，深部地层电阻率反演结果与模型真电阻率吻合很好。

图10所示为含cnoise=0.3高斯噪声的反演结果，由图可见，拟合误差和拉格朗日乘子随着迭代次数逐渐下降，在8次迭代后，拟合均方根相对误差就逐渐趋于稳定。与图9a不同的是，由于噪声信号强度较大，虽然能够刻画出地下电阻率变化趋势，但深部地层电阻率反演结果与模型电真阻率差别较大。对比图9b和图10b可以看出，噪声信号强度会影响拟合均方根相对误差，噪声信号越强，最终的拟合误差越大。

图9 cnoise=0.1高斯随机噪声HK型模型反演结果 Fig.9 Inversion results of HK model with cnoise=0.1 Gaussian noise

图10 cnoise=0.3高斯随机噪声HK型模型反演结果Fig.10 Inversion results of HK model with cnoise=0.3 Gaussian noise

5 结论

本文基于垂直分量研究了带约束的多辐射场源地空瞬变电磁一维自适应正则化反演方法，并将其分别应用于含噪和不含噪一维层状模型数据的反演，得出如下结论。

1)该算法基于Occam反演，采用CMD自适应拉格朗日乘子调节方案改进拉格朗日乘子的处理方式，并利用自然边界条件和模型修正量可行下降方向法对反演过程进行约束，减少反演过程的计算量，提高反演效率，计算速度快，收敛稳定，经过10次左右的迭代，已能获得较为理想的反演结果。

2)层状模型反演结果表明该算法可以获得光滑稳定的反演结果，对于典型的H、K型三层模型和HK型四层模型均能获得较好的反演结果，该算法对于复杂地电构造仍具有较好的适应性和有效性；受低阻层屏蔽作用和对高阻体不灵敏的影响，该算法对高阻层的反演仅能获得下部地层的平均电阻率值。

3)噪声信号大小会影响反演结果，噪声越大，对反演结果的影响越大，由于本文添加的高斯随机噪声表现为晚期数据信噪比低，噪声对反演结果的影响主要体现在深部地层电阻率反演结果上；噪声同样会影响拟合均方根相对误差，噪声越大，最终的拟合误差越大。