基于断裂力学的反倾岩质边坡倾倒破坏分析

王 林 华

(安徽省水利部淮河水利委员会水利科学研究院， 安徽 合肥 230022)

在地质构造和外界营力作用下，地表岩层产状各异。当岩层的倾向与坡面相反，该类边坡为反倾岩质边坡，其失稳破坏模式一般为倾倒破坏。Goodman等[1]最早将倾倒破坏分为块体倾倒、弯曲倾倒、块体弯曲倾倒和次生倾倒4种类型，然后众多学者对各类型破坏模式展开研究。基于极限平衡原理，Hoek等[2]针对块体倾倒建立了稳定性分析方法，Aydan等[3]利用悬臂梁模型对弯曲倾倒破坏进行了分析，Amini等[4]结合上述两类方法建立了块体弯曲倾倒破坏分析方法。国内外学者针对上述理论分析方法进行了改进：Sagaseta等[5]、Liu等[6-7]提出了连续介质分析方法研究岩块长细比较大、岩层较多时的块体倾倒破坏稳定性，该方法计算简便，无需迭代计算；陈从新等[8]结合室内模型试验和数值模拟结果提出弯曲倾倒破坏中坡趾岩层剪切破坏的可能，并将破裂面上岩层划分为滑移区、叠合倾倒区和悬臂倾倒区；Adhikary等[9]通过离心试验结果对Aydan的方法进行了改进，并提出破裂面方向应当垂直岩层方向向上一定的角度；Zhao等[10]基于变形协调条件分析了非等刚度下反倾岩质边坡的稳定性；庄冬梅等[11]基于ArcGIS、UDEC和监测位移结果，分析边坡倾倒变形的演化过程；刘汉东等[12]通过振动台试验研究反倾边坡的动力变形破坏特征。

在以往研究中，为了便于计算，假设其地质模型中破裂面上的岩层完好或与母岩完全断开。而在实际边坡中，岩体往往存在大量的节理和裂隙，这些节理、裂隙并不是完全贯通，如图1所示。Zhang等[13]、陈祖煜等[14]基于该类工况对Goodman法进行了改进，但未从断裂力学的角度分析该类边坡稳定性。Majdi等[15]根据Amini等[16]在2009年提出的等效长度法进一步讨论非贯通横向节理对边坡稳定性的影响，却未考虑岩层剪切破坏的可能。此外，王林峰等[17]、王建明等[18]基于断裂力学理论对边坡中单个岩层进行力学分析，考虑了拉力、剪力和弯矩的共同作用，探讨了边坡中岩层的破坏顺序，却很难判定边坡整体的稳定性。针对以上不足，本文拟考虑一组非贯通横向节理切割的工况，运用极限平衡原理和不同的破坏准则，推导出该类型边坡稳定性分析方法。

图1 雅砻江地区反倾岩质边坡[19]

1 倾倒破坏分析方法的建立

自然界的岩体往往存在各种不规则的节理、裂隙等非连续面，破坏了岩体的完整性，而这些非连续面当中，岩层的破坏往往由一条主控裂纹决定[20-23]。Jennings[24]在分析岩质边坡平面破坏时，用统计学方法得出岩体中节理连通率，用来表示地质结构缺陷，其计算公式如下：

(1)

式中：k表示横向节理连通率，aj为岩层j的横向节理长度，cj为岩桥长度，N表示节理总个数。在现场测量潜在破裂面附近的节理和岩桥长度，然后利用统计学的方法得出岩层j的横向节理连通率k。为便于力学分析，将边坡中岩层j近似为一个带横向裂纹的悬臂梁，如图2所示。

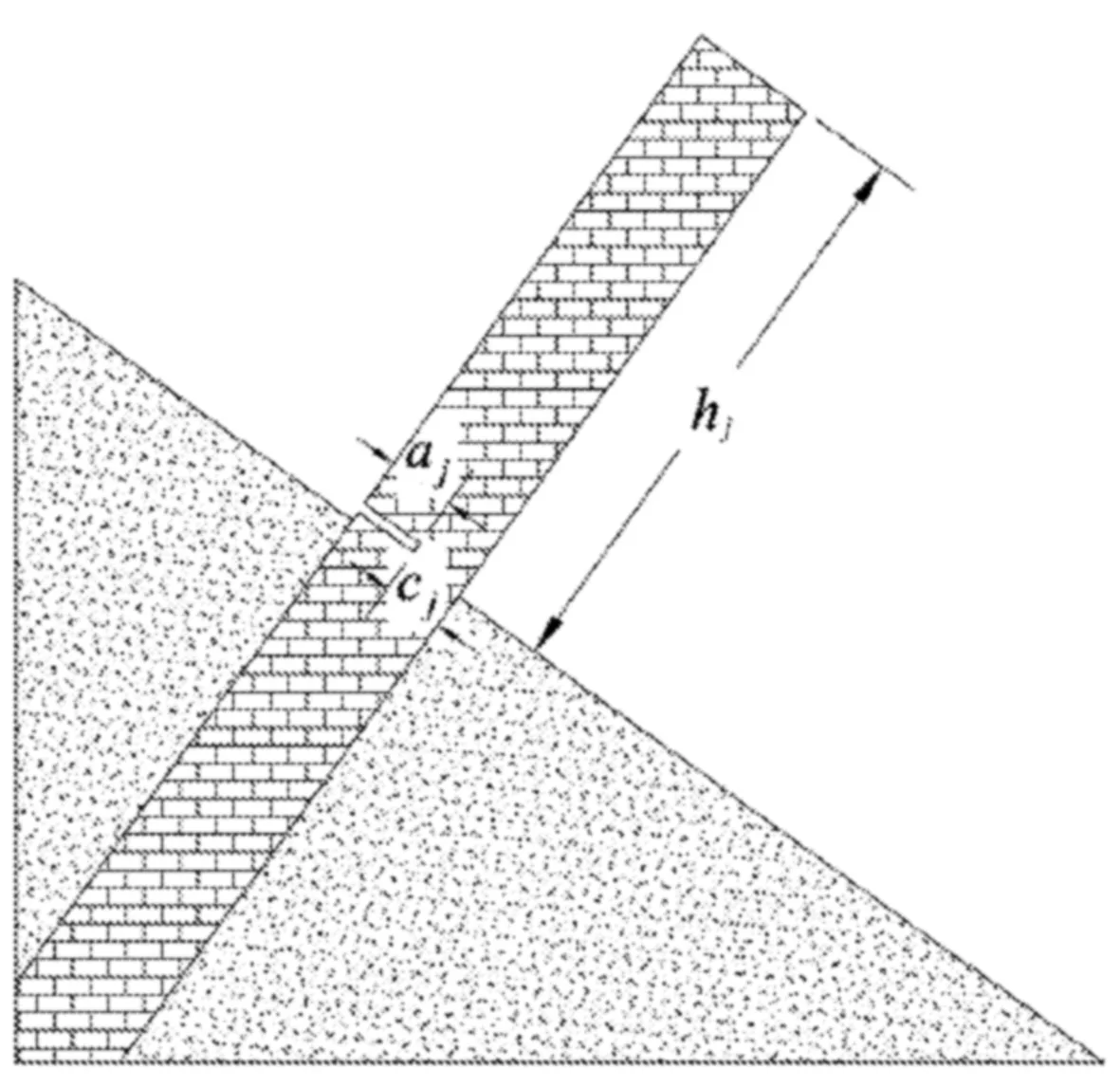
图2 反倾岩质边坡中岩层j的简化模型

1.1 基本假设

本文采用以下几条基本假设来简化倾倒破坏的分析过程：

(1) 倾倒破坏面为一直线，且垂直岩层方向向上一定角度θ。

(2) 破裂面上岩层具有相同的安全系数Fs，且都为边坡的整体安全系数。

(3) 相邻岩层界面上层间剪力满足极限摩擦平衡条件。

(4) 边坡中岩层的厚度和横向节理连通率k相同，非贯通横向节理位于破裂基准面上岩层层底受拉侧。

在常用的块体倾倒和弯曲倾倒分析模型中，破裂面上的岩层应划分为稳定区、倾倒区和剪切滑移区三部分。对于含有非贯通横向节理的反倾岩质边坡，也应存在这三个区域，如图3所示。对不同破坏模式的岩层，应采用不同的平衡方程进行计算。图中H表示边坡高度，α为岩层倾角，βc表示切坡角度，βs表示自然坡度，bj为岩层j的厚度，θ为破裂面与岩层法线的夹角。

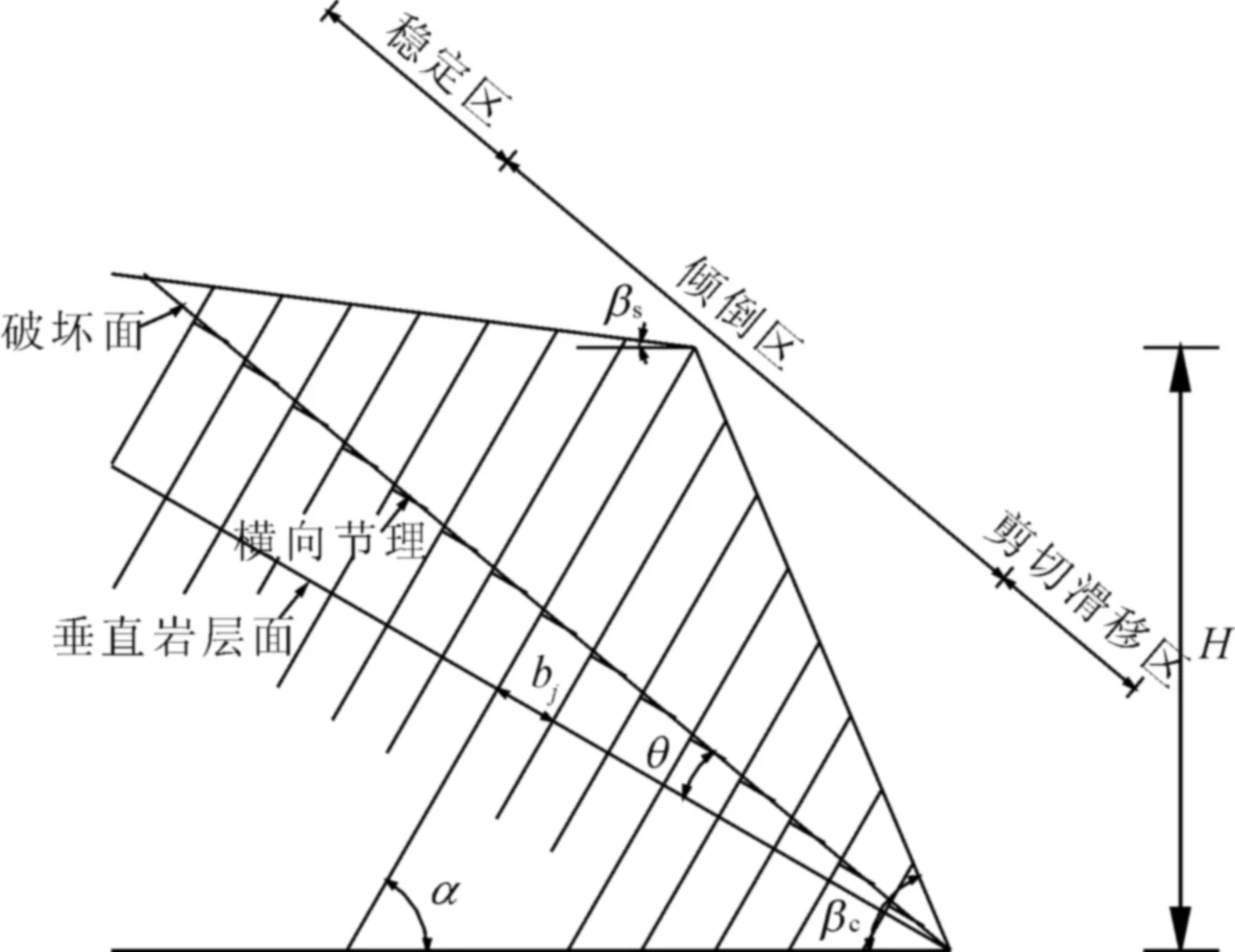
图3 考虑非贯通横向节理的反倾岩质边坡地质模型

1.2 力学分析

1.2.1 倾倒区岩层

在自重、地震力等作用下，岩层产生弯曲应力，当拉应力超过岩石抗拉强度时发生弯曲折断，该类破坏属于Ⅰ型断裂。Ⅰ型断裂韧度KIC是重要的材料参数，该真实材料参数的获取一直是近年来学者广泛关注的热点问题。根据单边开口梁断裂试验结果，Hu等[25-26]先后提出边界效应、尺寸效应对材料断裂韧度的影响，在此基础上管俊峰等[27-28]将平均颗粒尺寸引入断裂模型，确定出满足条件的最小试件尺寸。

文中为计算简便，忽略尺寸效应、颗粒大小对断裂韧度的影响。边界效应理论认为：当试件宽度远大于裂缝长度时，材料力学的破坏准则发挥主导作用。当裂缝长度接近试件宽度时，其破坏受断裂韧度准则控制。边坡中岩体受力形式复杂，不能简单看成三点弯曲试验来直接利用上述的结论。首先应根据力的平衡关系，求出岩体在不同破坏准则下的等效层间力。

图4为倾倒破坏模式下岩层j的受力图。若岩体的破坏受材料力学的强度准则控制，根据力矩平衡，此时岩层j的剩余下滑力为：

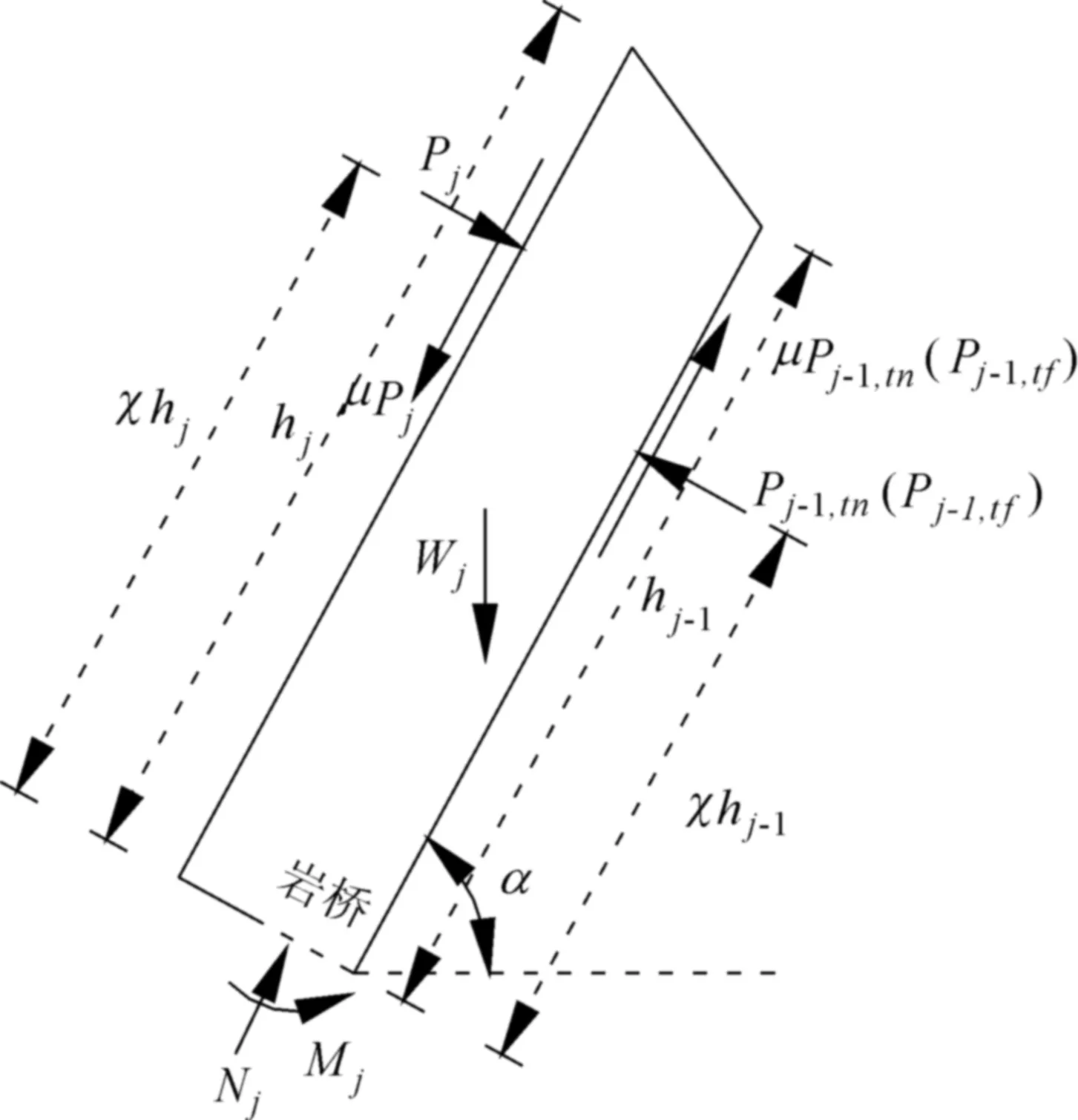
图4 岩层j倾倒破坏力学分析模型

(2)

当岩层j由断裂力学破坏准则控制时，岩层为偏心受压构件，应考虑弯矩和压应力的联合作用。由应力强度因子手册[29]可知，在纯弯状态下应力强度因子为：

(3)

YIM(k)=1.122-1.40k+7.33k2-13.08k3+

14.00k4

(4)

根据平衡方程可得，岩层j底部所受的弯矩Mj大小为：

(5)

在压应力作用下产生的应力强度因子为：

(6)

YIσ(k)=1.12-0.231k+10.55k2-21.72k3+

30.39k4

(7)

根据平衡方程可得，岩层j底部所受的压力Nj大小为：

(8)

对于偏心受压的岩层，裂缝尖端的应力强度因子应是两种简单荷载作用下的应力强度因子的叠加，故断裂韧度KIC为：

(9)

将式(5)、式(8)代入式(9)中，可得在断裂力学模型中岩层j向下传递的剩余下滑力Pj-1,tf为：

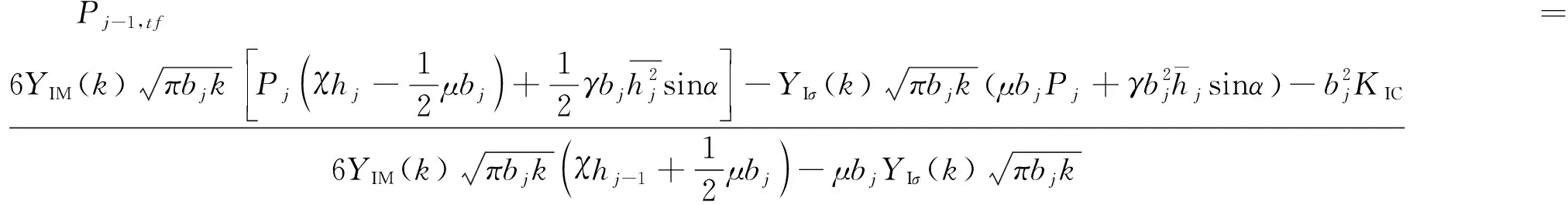
(10)

1.2.2 剪切滑移区岩层

在坡趾处的岩层长细比较小，不容易发生弯曲折断，在上部推力作用下存在剪切滑移的可能。图5为岩层j在剪切滑移状态下的受力图。由材料力学可知，岩层j在剪切滑移状态时的剩余下滑力Pj-1,sn为：

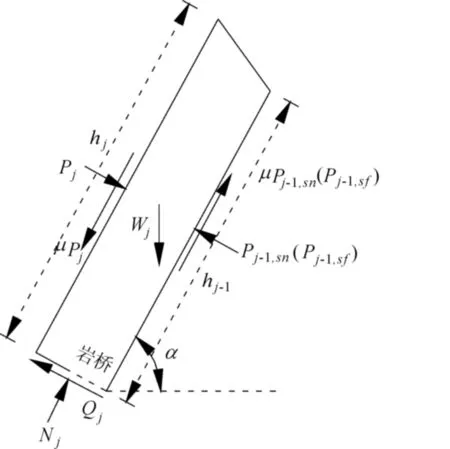
图5 岩层j剪切滑移破坏力学分析模型

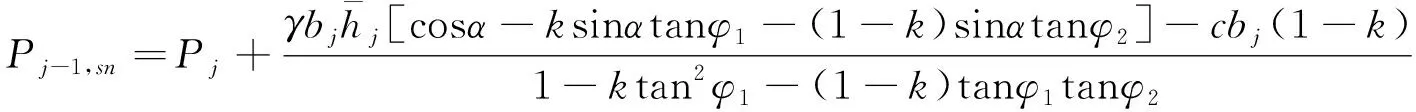
(11)

式中：Pj-1,sn为岩层j在强度破坏准则时下侧受到的法向力；φ1为岩层层面摩擦角；c和φ2为岩层内黏聚力和内摩擦角。

当岩层由断裂准则控制时，由应力强度因子手册[30]可知，在纯剪状态下应力强度因子为：

(12)

(13)

根据平衡方程可得，岩层j底部所受的剪力Qj大小为：

(14)

将式(14)代入式(12)中可得在Ⅱ型剪切断裂破坏模式下，岩层j的剩余下滑力Pj-1,sf为：

(15)

上述推导了不同破坏区岩层在不同强度准则控制下向下传递的层间力，岩层j的破坏模式可由剩余下滑力的值确定，通过式(2)、式(10)、式(11)和式(15)计算各种工况下的Pj-1值，其中最大值对应工况应为岩层实际破坏工况，若所有工况下岩层的剩余下滑力皆为负值，则岩层j能够抵抗上推力及自身重力的作用，保持稳定，剩余下滑力为0，因此剩余下滑力Pj-1为：

Pj-1=max(Pj-1,tn,Pj-1,tf,Pj-1,sn,Pj-1,sf,0)

(16)

1.3 边坡稳定性分析

本文采用从坡顶自上而下进行迭代计算岩层间传递的等效作用力，最终通过坡趾处岩层的剩余下滑力P0确定边坡稳定性。

(17)

通过上述公式可以得出边坡是否稳定，但仍需确定边坡的整体安全系数。采用强度折减法，将岩体和岩层层面强度参数σt，c1tanφ1，tanφ2，KIC和KⅡc同时除以Fs，并计算坡脚处P0的值，当P0为0时所对应的Fs的值即为边坡整体安全系数。

2 实例分析

上述推导了断裂力学模型下岩质边坡倾倒破坏的解析过程，以下以Majdi等[15]中的Galandrood地区某矿山岩质边坡为例来验证本文所提的方法，该边坡的计算参数见表1。Aydan等[3]和Amini等[4]倾倒破坏的稳定性分析方法过程中层间法向力作用点系数χ=0.75，故本文算例中χ取0.75。

表1 Galandrood反倾边坡稳定性计算参数

图6中Galandrood矿山反倾岩质边坡存在明显的横向节理，边坡上部发生局部破坏，但是整体保持稳定。Majdi等[15]通过实地调查和监测结果认为该边坡处于临界失稳状态，其安全系数值应接近于1。利用本文所提计算分析方法，边坡安全系数为1.08，与工程实际相符。若不考虑横向节理的影响，边坡整体安全系数为2.18，明显高估了边坡稳定性。同时Majdi等根据等效长度法，讨论了横向裂纹对边坡稳定性的影响，计算得出该边坡的安全系数为1.18，本文方法的计算结果较Majdi法更为准确。

图6 Galandrood矿山边坡[15]

3 参数分析

以上述矿山边坡为例，研究节理连通率，切坡角度和岩层厚度对边坡稳定性的影响。在该类边坡稳定性计算时，破裂面的角度应当根据实际边坡倾倒变形确定。对未明显倾倒变形的边坡, Adhikary等[9]提出用垂直岩层面向上10°的平面进行计算，陈从新等[8]提出用破坏面搜索法找出安全系数最小的破坏面，而一般情况下，破坏面垂直岩层面时边坡的安全系数最小。本文为简化计算，均采用垂直岩层方向向上10°的平面作为破坏基准面。

3.1 节理连通率对边坡稳定性和滑动比例系数的影响

本文当中的形状系数YIM和YIσ在k≤0.6时精确度较高[30]，故k取0.1～0.6。由图7可知，随着横向节理连通率的增加，边坡的安全系数逐渐减小，从1.42减小为0.83，可以看出横向节理对反倾岩质边坡稳定性有显著影响。同时若只用强度准则计算边坡安全系数，往往会高估边坡稳定性。图8为k=0.5时，等效层间力在岩层间的传递。其中等效层间力从坡顶自上而下先增加后减少，减小区在坡顶岩层以下，说明坡脚处岩层为倾倒破坏的抗滑段，这与赵维等[30]的结论相符。表2为弯曲倾倒区和剪切滑移区在不同节理连通率下的分布。由表2可知，随着连通率的增加，破坏区的范围增大且坡趾处的滑动比例系数增加。

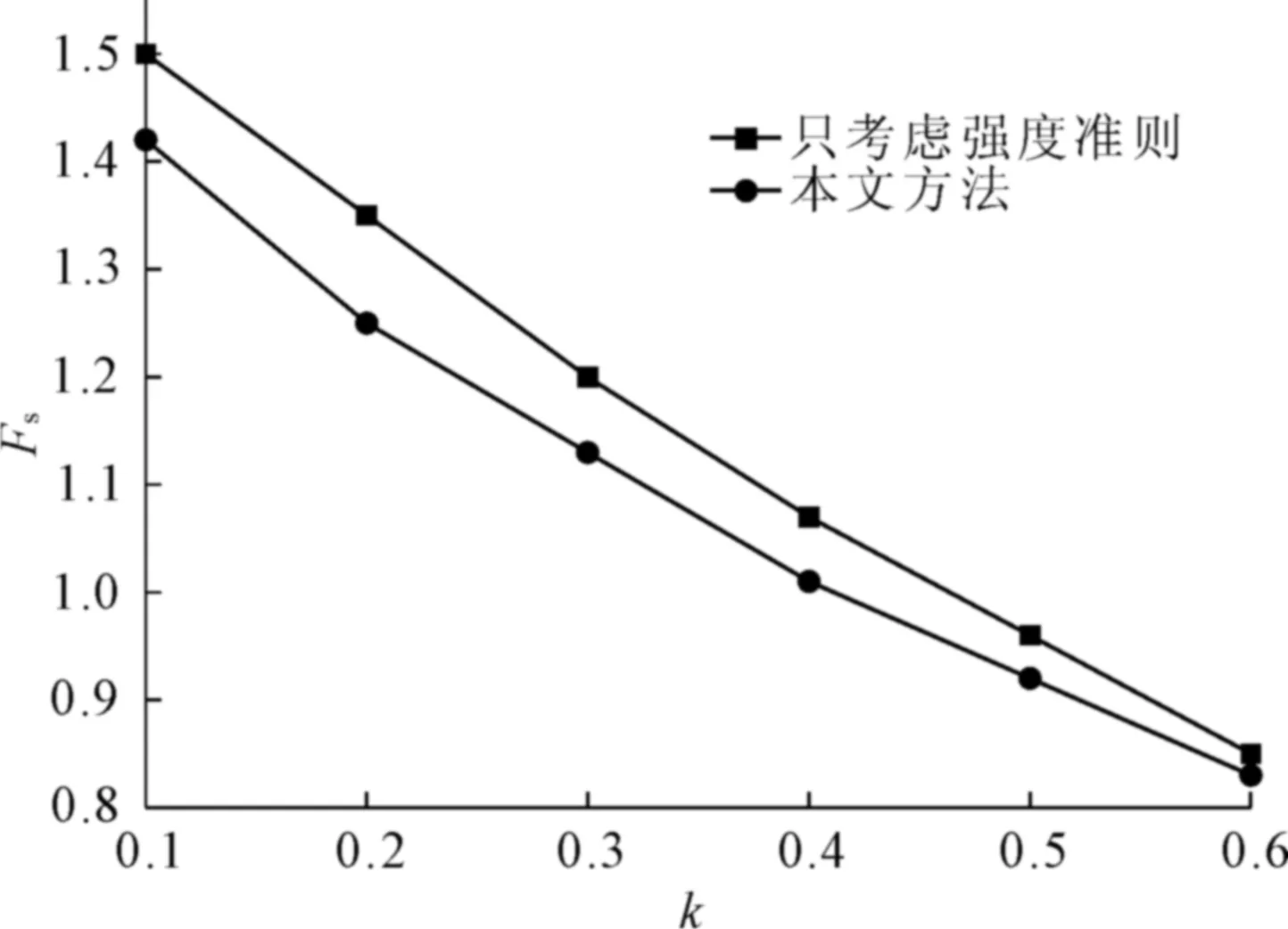
图7 横向节理连通率和边坡安全系数的关系曲线

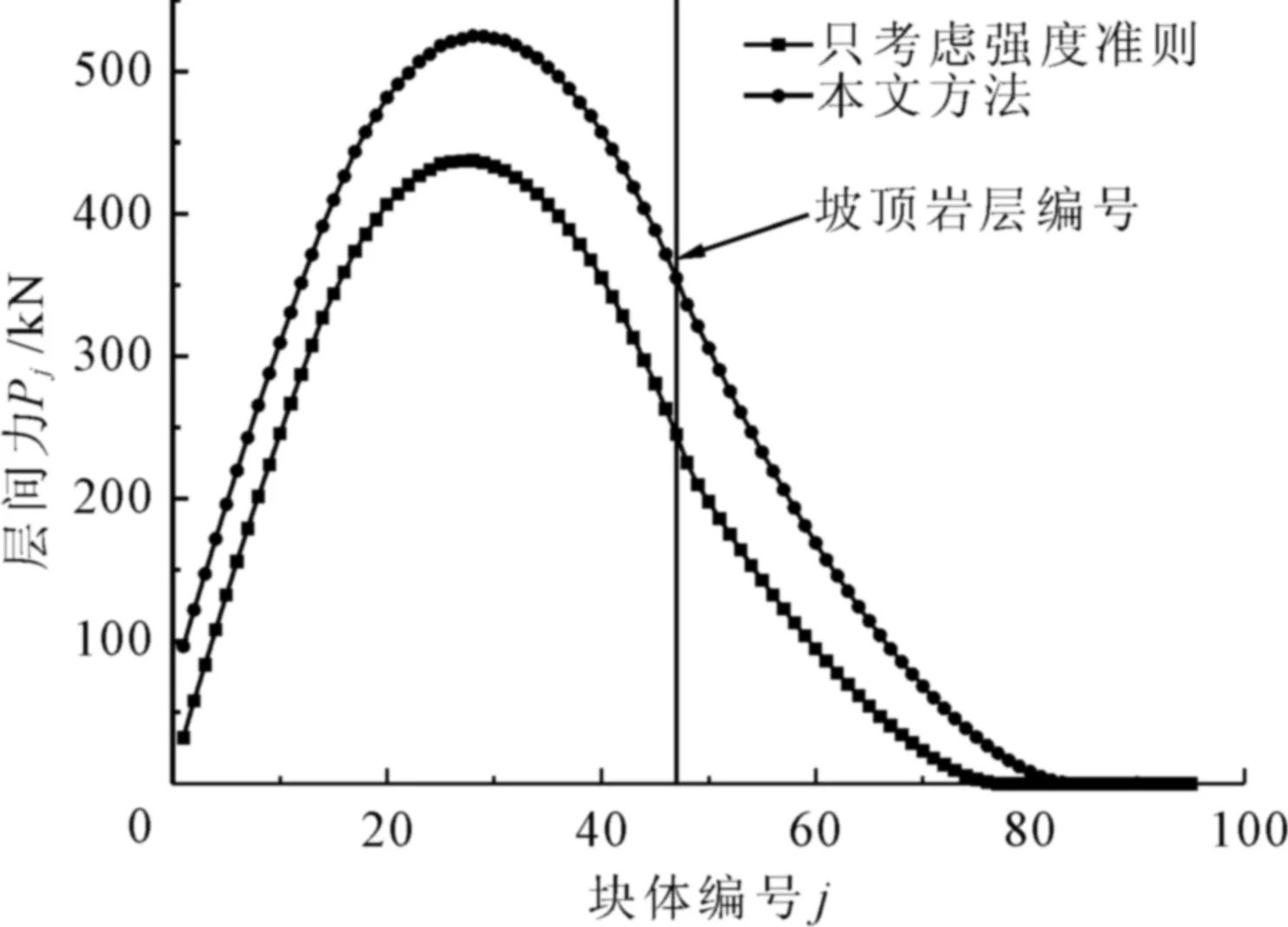
图8 横向节理k=0.5时岩层间的等效层间力

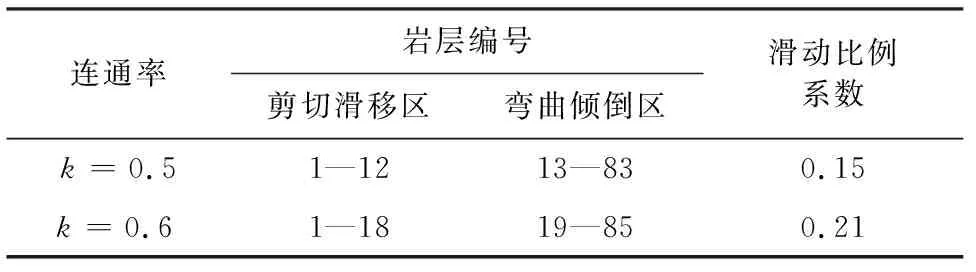
表2 边坡在不同横向节理连通率下破坏区的分布

3.2 岩层厚度对边坡稳定性的影响

岩层厚度b分别为0.2 m、0.3 m、0.5 m时不同横向节理连通率对边坡稳定性的影响如图9所示。

由图9可知，岩层厚度影响边坡稳定性。当岩层越厚，边坡的安全系数越高。但随着横向节理连通率的增加，岩层厚度的影响越不明显。当k=0.6时，三种厚度的岩质边坡安全系数在0.83左右，相差不超过±4%。故由趋势可知，当k大于0.6时，岩层厚度的变化对安全系数的影响不大。表3为不同厚度的岩质边坡在k=0.6时，不同破坏模式的岩层分布。由于边坡中岩层厚度不同造成了各岩层在破裂面上的个数不相同，岩层编号不能很好的表示破坏区范围的大小，故直接用弯曲倾倒区和剪切滑移区在破裂面上的长度表示。由该表可知，随着岩层厚度的增加，滑动比例系数增大，这是因为坡趾处岩层的长细比较小，容易发生剪切滑移破坏。同时滑动比例系数在0.1～0.3之间，这与陈从新等[8]的结论相符。

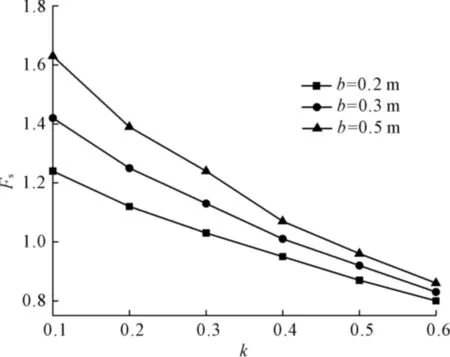
图9 不同厚度下横向节理连通率和边坡安全系数曲线

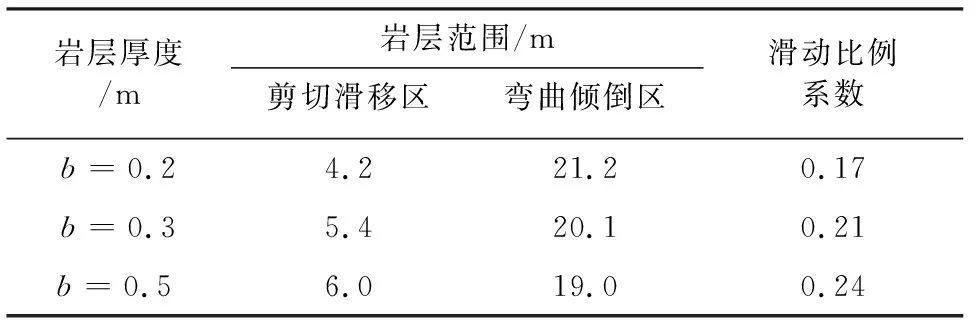
表3 k=0.6时边坡在不同岩层厚度下的破坏区分布

3.3 切坡角度对边坡稳定性的影响

切坡角度的变化可改变破裂面上岩层的高度。保持其它参数不变，切坡角度取81°,76°和71°三种工况，其结果如图10所示。由图可知，随着切坡角度的减小，边坡的安全系数增加，这是因为岩层的高度减小，由重力下滑分力造成的倾倒力矩减小，抗倾倒能力增大，不易发生倾倒破坏。图11为不同切坡角度的边坡在节理连通率为0.5时的等效层间力，x=0表示坡脚位置处，x=1为坡顶岩层位置。可以看出，切坡角度对岩层间的等效层间力影响显著。其切坡角度越大，边坡不稳定区域和等效层间力越大。

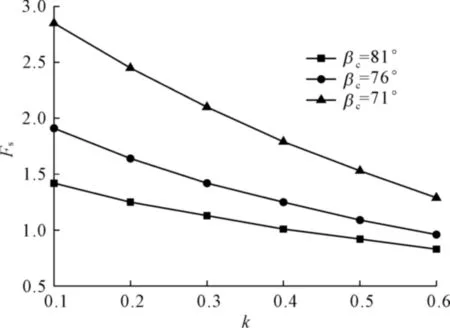
图10 不同切坡角度下横向节理连通率和边坡安全系数曲线

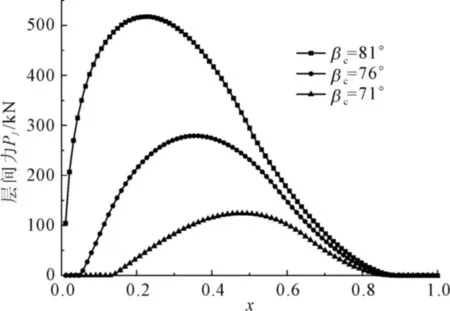
图11 不同切坡角度时岩层间的等效层间力

4 结 论

(1) 结合反倾岩质边坡中存在一组横向结构面切割的工况，讨论了岩层在倾倒破坏和剪切滑移两种破坏模式下等效层间力的传递，建立了该类边坡稳定性计算分析方法。

(2) 在横向裂纹的尖端应力集中，不能用完整岩体的抗拉、抗剪强度计算该类边坡稳定性；基于材料力学破坏准则计算该类边坡安全系数，往往会高估边坡稳定性。

(3) 随着横向节理连通率的增加，边坡稳定性相应变小；随着岩层厚度的增加，边坡的安全性随之提高，同时边坡的滑动比例系数增大；切坡角度的增加改变了破裂面上岩层的长细比，岩层的高度增加，其倾倒力矩增加，边坡的稳定性相应降低。

需要说明的是：在本文的计算方法中，横向结构面连通率k的选择非常关键，应结合现场调查和工程经验综合考虑。此外，本文在断裂力学模型分析中，为简化计算，未考虑弯矩、压力和剪力的联合作用。