数形结合思想在小学数学中的应用

朱嘉松 刘燕萍

【摘要】本文以面积解题为例，论述在小学数学教学中运用数形结合思想解决数学问题的策略，用面积解题帮助学生理解运算定律、解平均数、求租船问题、进行数的计算等，有效地解决数学问题。

【关键词】数形结合 面积解题 小学数学

【中图分类号】G 【文献标识码】A

【文章编号】0450-9889（2021）25-0095-02

数学家华罗庚说：“数缺形时少直觉，形少数时难入微。”在小学数学教学中，数与形是数学研究的两个重要方面，数形结合既是一种常用的教学方法，又是重要的数学思想。针对小学生逻辑思维能力不强，面对抽象复杂的问题缺乏理解力和分析力的问题，数学课堂运用数形结合思想，可以将抽象的数学问题变得形象直观，使繁难的数学问题简单明了。下面，以巧用面积解题的方式让学生在直观理解的基础上，充分感知抽象运算的过程，达到以简驭繁有效解决数学问题的目的。

一、用面积解题帮助学生理解运算定律

数与形关系密切。在运算定律教学过程中，笔者运用教学图形巧妙地把数和形结合起来，利用面积解题指导学生理解运算定律，掌握计算方法，把抽象的数学概念直观化，把抽象的问题形象化，帮助学生理解数学概念的本质特征。如教学乘法分配律（一个数乘两个数的和，等于这个数分别与这两个数所得的积的和）时，部分学生在运用乘法分配律进行简便运算时总是出错，且不会分析错误的原因，对算理的理解基本处于无意识状态。小学生思维的发展，正逐步从具体形象思维向抽象思维过渡，由于乘法分配律这一部分内容抽象性较强，学生学起来确实有难度，怎样才能突破这一教学难点呢？传统的教学方法是强背概念和大量练习，这样的教学往往事倍功半。对此可以运用数形结合思想方法，以面积解题的方式帮助学生理解运算定律。

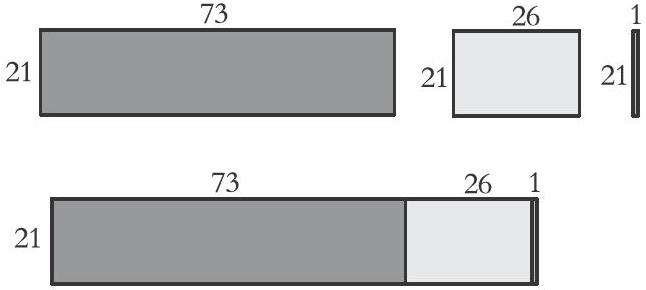
例1：下列三个长方形面积之和，等于把三个长方形拼成一个长方形的面积。（单位：厘米）

得出：21×73+21×26+21×1

=21×（73+26+1）

=21×100

=2100（平方厘米）

将三个长方形拼成一个大长方形，呈现一个直观性和操作性较强的素材图，使得学生更易于掌握乘法分配律。

二、用面积解题帮助学生解平均数

在总和不变的条件下，把几个不相等的数通过移多补少，使它们完全相等，得到的数就是平均数。学生在做一般的平均数问题时，只须牢记三个数量关系式，即平均数=总数量÷总份数，总数量=平均数×总份数，总份数=总数量÷平均数。但在实际运用中遇到较复杂的平均数问题时，学生虽然懂得要“移多补少”，但不知道将移去的部分补到哪里，移补前后哪些数据发生了变化，导致做题时很茫然。对此，教师可以利用面积解题的方式帮助学生解平均数。下面以一道数学题为例谈谈教学实践。

例2：一次语文测试，四年级（2）班全体同学平均分为92.5分，已知女生20人，平均每人94分，男生平均每人91.3分，求这个班男生有多少人？

在教学中，笔者利用图“形”作为直观工具帮助学生分析、理解问题，即通过画图用面积公式来求平均数问题。解题过程如下：

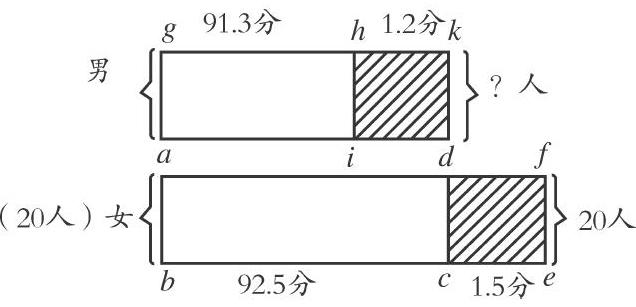
将平均分看作长方形的“长”，将人数看作长方形的“宽”，总分就自然可以当作长方形的“面积”。如图所示：

用线段gh表示男生平均分数91.3分，线段bc则表示全班平均分数92.5分，线段be表示女生平均分数94分，线段ab表示女生人数20人，线段ag表示男生的人数（横线的长短表示平均数的多少，竖线的长短表示人数的多少）。求男生人数是多少，即求线段ag长多少？由平均数的“移多补少”可知，长方形dcef的面积是女生高出全班平均分的部分，它正好补到男生低于全班平均分的那一部分，也就是长方形idkh的面积，由此可知，长方形dcef的面积等于长方形idkh的面积，这样就能将其转换成用长方形的面积公式来求问题。由图形可知，男生人数ag，正是长方形idkh的宽边。解题过程应先求出女生高出全班平均分的總分数，如下：

长方形dcef的面积=长×宽

=（94-92.5）×20

=30（分）

因为长方形dcef的面积表示女生高出总平均分的总分数，所以30的单位是“分”。这个面积与长方形idkh的面积相等：

宽ag=宽dk=长方形dcef的面积÷长hk

=30÷（92.5-91.3）

=25（人）

因为线段ag的长表示男生的人数，所以25的单位是“人”，也就是说男生有25人。列综合算式为：

20×（94-92.5）÷（92.5-91.3）

=30÷1.2

=25（人）

答：这个班男生有25人。

对两批学生用新老方法进行教学可知，画图移补面积的方法更能让学生直观形象地接受并掌握知识点。

三、用面积解题帮助学生求租船问题

图形的直观形象特点，决定了化数为形往往能达到以简驭繁的目的。如利用面积解题策略可以帮助学生理解如何调整船只，让学生在直观理解的基础上充分感知调整的过程，从而提升思维能力。

例3：全班同学去划船。如果减少一条船，每条船正好坐9人;如果增加一条船，每条船正好坐6人。那么全班共有多少人？

在教学时，教师的解题策略侧重于先假设有x条船，减少一条船，每条船坐9人与增加一条船正好坐6人的总人数相等，利用关系式列出下列方程。

方法1：设有x条船。

9×（x-1）=6×（x+1）

9x-9=6x+6

9x-6x=6+9

3x=15

x=5

全班共有9×（5-1）=36（人）

答：全班共有36人。

方法2：将每条船上的人数看作长方形的“长”，船数看作长方形的“宽”，从而将总人数自然看作长方形的“面积”。

分析：把C+B的面积看作总人数，将横线的长短看作每条船上的人数，竖线的高矮看作船数。因为增加一条船，每条船正好坐9人，所以ab的长等于9人，而减少一条船，每条船正好坐6人，de的长等于6人，dc的长等于2条船，增加一条船和减少一条船的情况下，二者相差两条船，可得：

面积C+B=A+C[]A=B

阴影A的面积=2×6=12（人）

阴影B的宽=12÷3=4（条）

总人数=4×9=36（人）

四、用面积解题帮助学生计算数

在小学数学教学中，有相当一部分内容是计算问题，计算教学要引导学生理解算理。数和数之间的运算本身是很抽象的，教师要引导学生通过以形助数的方法体会数形结合的直观生动性，感受数学学习的趣味性。巧用“几何意义”来解题时，可以观察、寻找图形的特点，从不同角度观察得出所求之数。这样很多学生就会对数学思维产生新的认识和体会，从中直观感受到数学的“美”。

例4：两个自然数，它们的和加上它们的积恰为34，那么这两个数中较小的数是多少？

分析：利用长方形面积的定义，特别是巧用“1”作为两个小长方形的宽。

a+b+a×b=34

a×1+b×1+a×b=34

如图：

（a+1）×（b+1）=34+1=35=5×7

a+1=5，（b+1）=7，即a=4，b=6

结合以上例子，学生逐渐明白了数形结合之间的关系、利用面积解题前后的情况变化，对面积公式能够运用自如，这样学生在解决问题时更得心应手。

总之，利用面积解题帮助学生理解“租船问题和简便运算、解决求平均数和数”问题，其实是借助形的几何直观性来阐明几个数之间的关系，这就是数形结合思想中的“以形助数”，它有利于协调发展学生的抽象思维、形象思维，优化解决问题的方法。教师在教学中遇到难讲的题目时，可以找一找数和形之间的对应关系，通过数与形的相互转化来解决问题，从而得到一条捷径，促使学生学得轻松愉快，更加有效地解决数学问题。

注：本文系广西教育科学“十三五”规划课题“美术效应在小学数学教學中的价值研究”（编号：2017C253）的研究成果。

【作者简介】朱嘉松（1968— ），男，汉族，广西贺州人，高级教师，贺州市平桂区黄田镇里宁小学科技辅导员，研究方向为中小学数学教育、美术教育;刘燕萍（1970— ），女，汉族，广西贺州人，高级教师，研究方向为中小学数学教育。

（责编 杨 春）