勾股定理不同证明方法的价值与思考

韩诗贵

摘  要：在教学中，要实现勾股定理不同证明方法的教育价值，需要教师进行整体设计. 文章从初识定理证明、体会勾股定理证明方法的多样性、后续教学中偶遇勾股定理证明等方面，分别阐述了勾股定理证明的价值与思考.

关键词：勾股定理证明;数学文化;教育价值

从被发现至今，人类对勾股定理证明的探索从未间断过. 人们曾先后对勾股定理给出了四百余种证明方法，这在数学史上是独一无二的. 四百余种证明方法在数学史上形成了一道靓丽的风景线，体现了勾股定理的与众不同，也承载了丰富的数学文化与教育价值.

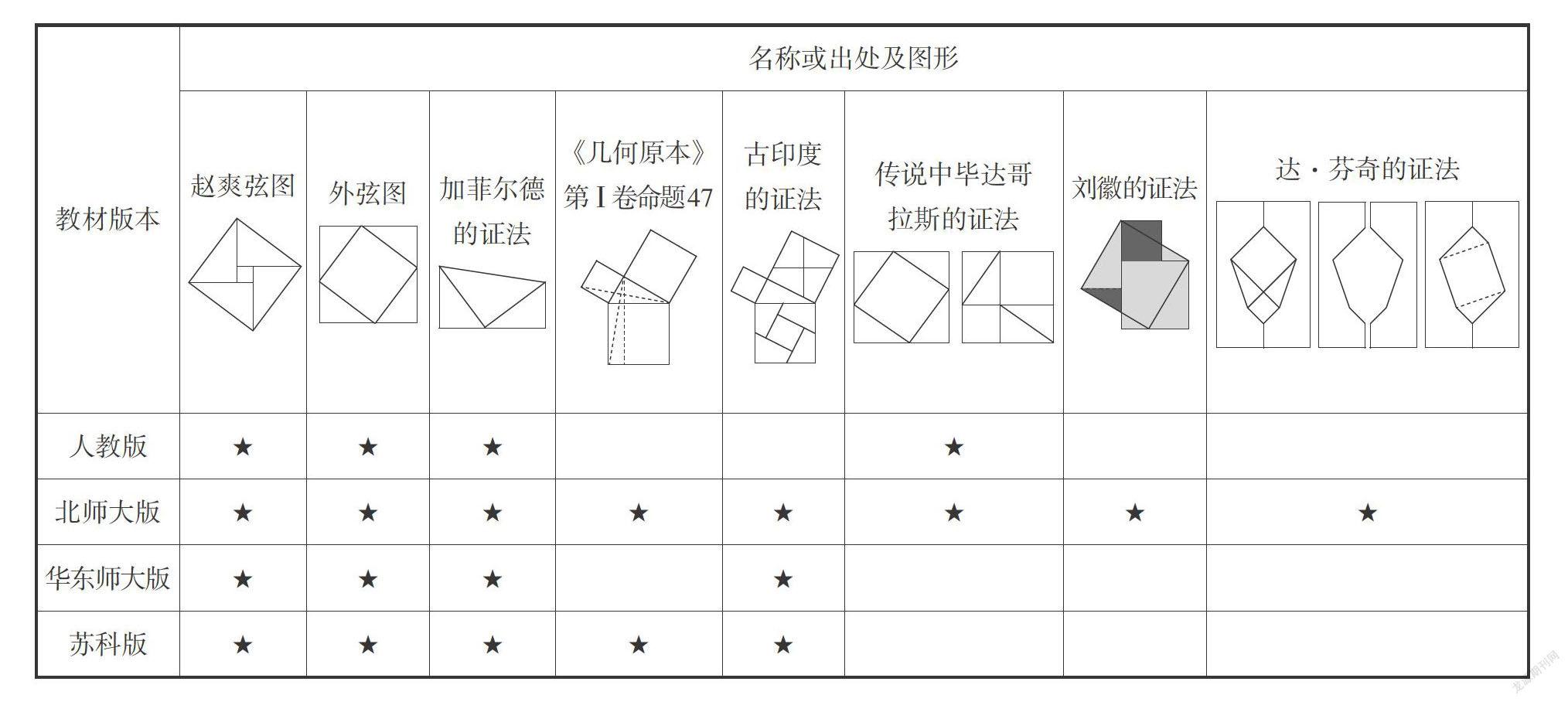
在当前使用的人教版、北师大版、华东师大版和苏科版等初中数学教材中，都介绍了多种勾股定理的证明方法. 一般地，在首次介绍勾股定理的证明时，都选用了赵爽弦图，随后分别出现了外弦图、加菲尔德的证法等常见的证明方法. 详细情况如下表所示.

在教与学的过程中，教师应该如何介绍勾股定理的证明才能传承数学文化，实现数学的育人价值呢？笔者结合具体的教学实践，谈一些粗浅的思考，不足之处，敬请指正.

一、在初识勾股定理证明中传承数学文化

赵爽弦图是中国有记载的、最早的证明勾股定理的方法. 2002年在北京召开的国际数学家大会便是将赵爽弦图作为大会会标. 多数版本教材在介绍用赵爽弦图证明勾股定理时，都是借助图1利用代数式运算完

成的. 例如，[c2=4 ⋅ 12ab+b-a2=][2ab+a2+b2-2ab=][a2+b2，] 这样的证明过程应用了完全平方公式和合并同类项等知识，是数与形的完美结合. 证明过程符合八年级学生的认知特点，学生容易理解.

在利用赵爽弦图证明勾股定理时，教师还可以补充“割补”的证明方法. 如图2，把边长为a，b的两个正方形连在一起，它的面积是[a2+b2];这个图形可以分割成四个全等的直角三角形和一个正方形，把图2左右两个三角形移到图3中所示的位置，就会形成一个以c为边长的正方形，因为图2与图4都是由四个全等三角形和一个正方形组成，所以它们的面积相等，因此[a2+b2=c2.] 非常巧妙！

事实上，以中国为代表的东方古代数学家，提供了许多运用“割补”证明勾股定理的方法，与赵爽同时代的刘徽利用“青朱出入相补法”证明勾股定理. 如图5，以直角三角形的勾为边的正方形ABCD为朱方，以直角三

角形的股为边的正方形BGHP为青方，以直角三角形的弦为边的正方形AEFG为弦方. 将三角形“朱出”移到“朱入”，三角形“青出”移到“青入”，即得到“朱方 + 青方 = 弦方”. 清代数学家梅文鼎和华蘅芳对勾股定理也都有类似的证明，割补法在勾股定理的证明中独树一帜，是勾股文化不可或缺的一部分，也是中国智慧对人类数学的重要贡献之一. 因此，笔者认为在初识勾股定理证明的新授课中，介绍弦图的割补法是对中国传统文化的尊重与继承，也是爱国主义教育的素材.

二、体会勾股定理证明方法的多样性

在勾股定理四百余种证明方法中，欧几里得的《几何原本》第Ⅰ卷命题47应该是人类有文字明确记载的最早证明之一，比中国古代赵爽的证明早了约500年. 欧几里得的证明思路如下. 如图6，已知[△ABC]中，[∠ACB=90°，] 四边形BCDQ，四边形ACKJ，四边形ABFE分别为以BC，AC，AB为边长的正方形. 易证[△ABQ≌△FBC，] [S△ABQ=12S正方形BCDQ，] [S△FBC=12S矩形BFGH.] 所以[S正方形BCDQ=S矩形BFGH.] 同理，可得[S正方形ACKJ=][S矩形AEGH.] 所以[S正方形ACKJ+][S正方形BCDQ=][S正方形ABFE.] 所以[AC2+BC2=AB2.]这种证明方法虽然没有赵爽等人的证明简洁，但它是通过几何演绎推理完成的.

由于八年級学生知识基础及教学时间的限制，在勾股定理证明的教学中，让学生全面了解勾股定理的四百余种证法是不可能的，事实上也是没有必要的. 但是，无论是为了学习勾股定理的证明，了解勾股文化，还是为了拓展学生的思路，笔者认为，在勾股定理证明的教学中，教师可以向学生介绍《几何原本》第Ⅰ卷命题47的勾股定理证明方法，这也是八年级学生能理解的、为数不多的几何演绎证明方法.

《义务教育数学课程标准（2011年版）》（以下简称《标准》）明确指出，要引导学生探索证明同一个命题的不同思路和方法，进行比较和讨论，激发学生对数学证明的兴趣，发展学生思维的广阔性和灵活性. 在八年级勾股定理教学中，教师可以通过课堂教学、课后作业、拓展活动，或者延伸阅读的形式渗透不同类型的勾股定理证明方法. 例如，赵爽、刘徽等的割补法证明，加菲尔德等的数形结合的代数式运算证明，欧几里得的几何演绎证明，以及传说中毕达哥拉斯的证明，等等. 各种证明方法承载了勾股定理的历史和文化，不同的思路和方法是使学生体会证明方法多样性的良好素材. 同时，为学有余力的学生打开了一扇窗，这扇窗或许能开启他们对勾股定理证明的探索之路，激发他们研究数学的热情.

三、在偶遇勾股定理证明中展示数学魅力

在初中不同几何知识的教学中，有多次与勾股定理证明的“偶遇”. 例如，学习相似三角形时，“母子”型相似是常见的基本图形. 如图7，在[Rt△ABC]中，[∠ACB=90°，] 过点C作[CD⊥AB，] 垂足为点D，由此易证得三个常见的结论，即[AC2=AD ⋅ AB，] [BC2=BD ⋅ AB，] [CD2=][BD ⋅ AD，] 这是我们熟知的射影定理. 如果再进一步研究，将等式[AC2=AD ⋅ AB]与[BC2=BD ⋅ AB]的左右两边分别相加，则得到[AC2+BC2=AD ⋅ AB+BD ⋅][AB=AD+BD ⋅ AB=AB2.] 这也是证明勾股定理的方法，是《几何原本》第Ⅵ卷命题31的结论. 相似问题与勾股定理证明的“偶遇”，以及这种证明方法的文化背景，不仅展示了数学的魅力，也能激发学生学习数学的兴趣.

又如，在内切圆的教学中，我们通常会遇到如下问题. 如图8，在[Rt△ABC]中，[∠ACB=90°，] 斜边长为c，两条直角边长分别为a，b，⊙I是[△ABC]的内切圆，求内切圆的半径r. 如果让学生独立求解，一般都会出现两种不同的解答过程与结果. 第一种：由[a-r+][b-r=c，] 解得[r=][a+b-c2.] 第二种：由[12ar+12br+][12cr=12ab，] 解得[r=aba+b+c]. 教师除了让学生理解这两个结论的正确性之外，若能引导学生进一步计算[a+b-c2=aba+b+c，] 则可以得到[a+b-ca+b+c=2ab，] 即[a2+b2=][c2.] 这是一位西方学者在1900年前后提供的证明. 利用圆的相关知识又一次证明了勾股定理，尽管这只是教学中的“副产品”，但一切都水到渠成，没有突兀之感，也能使学生感受到推理论证的乐趣，体验数学的和谐之美.

此外，在圆的“切割线定理”的教学中，也有与勾股定理证明的“偶遇”. 篇幅所限，不再赘述，详情可参阅文[5].

《标准》指出，数学中有一些重要的内容、方法、思想是需要学生经历较长的认识过程，才能逐步理解和掌握的. 根据学生的年龄特征与知识积累，在遵循科学性的前提下，采用逐级递进、螺旋上升的原则教学. 勾股定理是初中数学的核心内容之一，在平面几何中有着极其重要的地位. 随着学生学习的深入和知识的积累，勾股定理的不同证明方法会逐渐呈现，教师在教学中要善于捕捉这样的契机，丰富勾股定理的证明方法，使学生体会到数学知识的和谐与统一，感受数学的魅力.

四、结束语

勾股定理是一个古老的定理，也是一个基础而重要的定理. 人们对勾股定理关注的热情始终未减，一代又一代喜爱数学的人从未停止探索，新的证明方法也层出不窮. 在教学中，教师对勾股定理证明的整体把握和阶段渗透有助于学生了解勾股定理证明的文化，感受人类探索的精神，激发数学研究的兴趣. 可以说，勾股定理的证明方法不仅是数学文化的素材，而且是数学育人的载体.

参考文献：

[1]中华人民共和国教育部制定. 义务教育数学课程标准（2011年版）[M]. 北京：北京师范大学出版社，2012.

[2] 李文林. 从赵爽弦图谈起[M]. 北京：高等教育出版社，2008.

[3] 马奥尔. 勾股定理：悠悠4000年的故事[M]. 冯速，译. 北京：人民邮电出版社，2010.

[4] 欧几里得. 13卷视图全本几何原本[M]. 燕晓东，译. 北京：人民日报出版社，2005.

[5]庞彦福. 推理螺旋上升  彰显深度学习：以“勾股定理”证明为例[J]. 中学数学教学参考（中旬），2017（5）：61-64.