矿山通风巷道风门后的风速分布特性研究①

胡建华，赵 阳，周 坦，肖红星，赵 磊

（1．中南大学 资源与安全工程学院，湖南 长沙410083；2．湖北三宁矿业有限公司，湖北 宜昌443000）

随着矿山信息化水平的逐步提高，矿井通风智能化已成为未来矿山发展的必然趋势［1］，通过对风机、风门、风窗等设备的智能调控，稳定、经济地向井下连续输送新鲜空气，消除有毒有害气体和矿井粉尘，实现井下按需智能供风［2－4］。精准监测井巷风速是实现矿山智能通风功能的关键技术之一。目前，多采用单点法或多点法测量巷道内风速，即在同一断面固定单个或多个传感器进行监测，其中单点法经济成本低、测点位置选择灵活，以单点风速准确表达平均风速已成为业界学者普遍关注的问题［5］。

已有的研究成果表明，无论是单点法还是多点法，传感器的测点位置受巷道内风速分布的影响较大，特别是自动风门、风窗等设施导致井巷内风流环境复杂，风速的分布特性对测点布控位置影响较大［6－11］，提高障碍物条件下井巷风速准确性至关重要。基于此，本文利用计算流体力学方法，以湖北某矿山含卷帘式自动风门巷道段为研究对象，分析巷道风速、风门开合程度、壁面粗糙度对风门后流场分布的规律，探究通风设施对风速测点的影响，为风门后传感器布置范围的确定以及障碍物条件下精准测风等提供理论支持。

1 障碍物对巷道风速分布的影响

1．1 自动风门

井下作业环境相对封闭，巷道内风速分布极易受环境影响，障碍物的存在会造成风速测量准确性降低。以卷帘式自动风门设置后形成的方形障碍物为例，障碍物附近的风流场可分为3个区域：位移区、空腔区和尾流区，如图1所示［12］。风流沿巷道方向遭遇障碍物后被切分出现分离，流场结构发生变化，风流向下偏移形成位移区；风流保持继续绕过障碍物流动的趋势，在障碍物背风面形成具有环绕回流现象的空腔区；由于边界层内动能损失，在空腔区的下风向形成了尾流区，在经过数倍障碍物高度的距离后逐渐消失，巷道风流逐渐恢复常态。

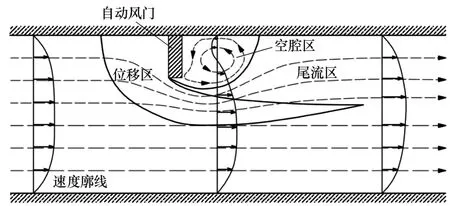
图1 障碍物后流场结构

空腔区风速发生损失，靠近巷道壁的风速方向改变，测量偏差较大；随着距障碍物距离逐渐增加，尾流区测量准确性提高，流场结构逐渐恢复。可见，影响风门后传感器测量精度的主要原因是存在空腔区和尾流区。研究风门不同开合程度下空腔区及尾流区的作用范围，对明确风门后传感器的水平范围具有重要意义。

1．2 粗糙壁面

采用单点法测量巷道风速时，施工等原因造成的粗糙壁面将造成流场结构的改变，影响测量准确性。如图2所示，粗糙度的存在增大了壁面阻力，使风能发生损失，在近壁面处形成一定范围的低速区域，靠近顶壁的传感器测量结果受到影响。

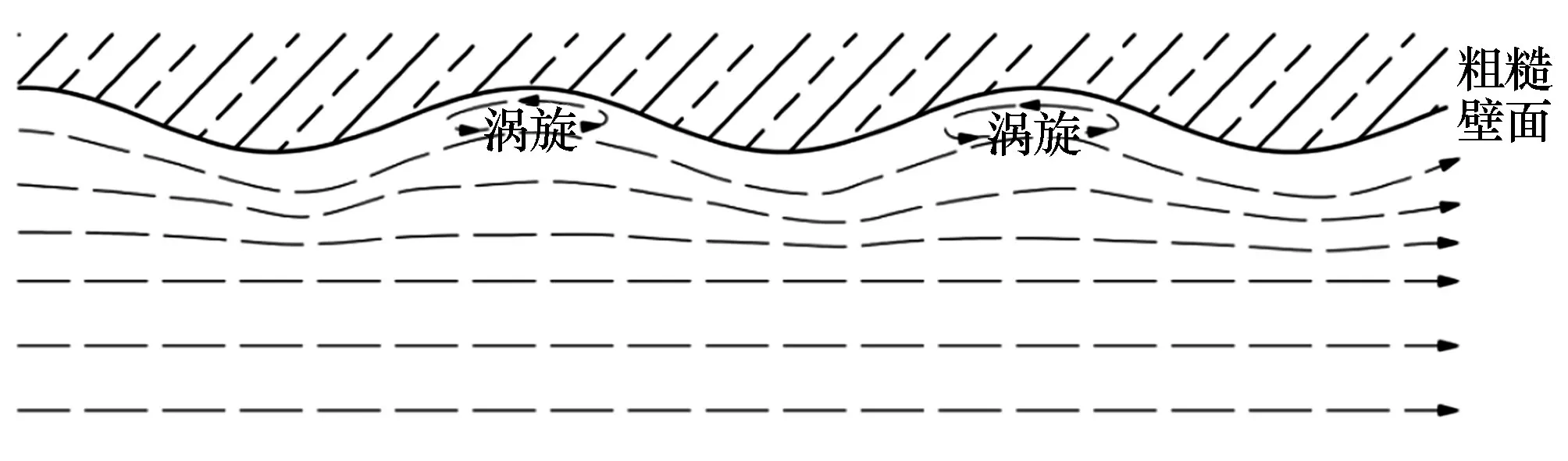
图2 粗糙壁面流场结构

实际粗糙表面多为三维，除二维粗糙表面的粗糙元形状、间隔、高度之外，还需考虑横向粗糙元间距、前后排粗糙元交错度等参数的影响［13］。由于传感器布置方向多与巷道断面垂直，风流沿巷道方向输送，粗糙表面对其影响可近似简化为二维模型。研究分析二维粗糙度下的风速波动范围，对确定传感器悬挂的最优竖直距离具有重要意义。

2 数值模拟

2．1 巷道几何模型

本次模拟的巷道实际断面为宽4 m、高3．5 m的矩形，卷帘式自动风门垂直巷道风流方向放置。风门厚5 mm，距顶壁30 cm，距侧壁15 cm，风门与巷道边壁之间采用木石、混凝土填充，无漏风现象，如图3所示。

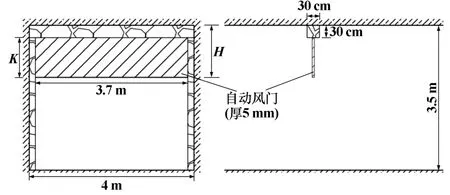
图3 巷道断面示意图

根据开合程度建立多种长度的巷道模型，以风门所在断面底边中点为坐标原点，沿巷道进风方向为X轴正向，垂直巷道底板向上方向为Y轴正向，水平方向为Z轴，建立长度为L1＋L2的矩形巷道模型，如图4所示。

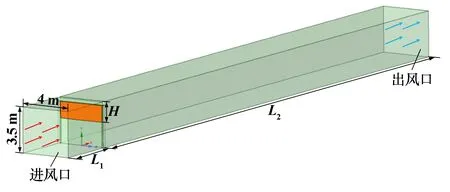
图4 巷道几何模型

为研究风门后顶壁粗糙程度对于测点位置的影响，以图4所建模型的光滑顶壁为巷道标准廓线，建立最大起伏程度为R的粗糙曲线。在实际生产过程中，对于开挖产生的较大起伏会进行相应的平整处理，故整体起伏高度较多地集中于标准巷道廓线附近，即曲线上点的R值较多趋于0。利用MATLAB生成期望值为0、标准差为R的正态分布数据，并将数据进行随机排列，以相同间距导入CAD中形成不同粗糙度的曲线。本次模拟生成长度L2、R分别为10 cm、20 cm和30 cm时的粗糙曲线，曲线示例如图5所示。

图5 不同粗糙度曲线示例

2．2 控制方程及计算模型

采用黏性不可压缩Navier-Stokes方程作为控制方程［14］，连续型方程及N-S方程可写为：

式中x j为坐标分量；i、j为张量分量；ρ为大气密度；p为气流相对压力；u i、u j为不同方向上的速度分量；f i为微元体在i方向上的单位质量力；υ为空气的动力黏性系数。

选择标准κ-ε湍流模型进行计算，湍流动能κ和动能耗散率ε分别由下式控制［14］：

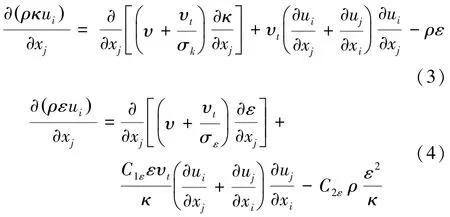
式中σk，σε，C1ε，C2ε均为经验常数，其中σk＝1．0，σε＝1．3，C1ε＝1．44，C2ε＝1．92。采用SIMPLE算法，迭代收敛标准为连续性残差降至10－6。

2．3 边界条件

由《金属非金属矿山安全规程》［15］关于井巷断面平均最高风速的规定可知，采场断面平均风速不超过4 m／s，运输巷道、采区进风道不超过6 m／s。因此，在本次计算中以1～6 m／s为主要模拟的巷道进口风速。

巷道进口设置为速度入口边界，只在进口有风流入，且不存在漏风现象，巷道出口采用压力出口边界。假设壁面固定，无滑移，气流与巷道壁面无热交换，且巷道内无工作人员、运输车辆等其他障碍物。巷道内空气视为不可压缩黏性紊流，空气密度1．2 kg／m3，忽略重力影响。

3 结果分析

3．1 进口风速的影响

考虑到传感器距巷道顶壁的悬挂位置，提取巷道中心线上Y＝3 m的模拟数据，研究进口风速的影响。建立长度100 m（L1＝15 m，L2＝85 m）、断面尺寸4 m×3．5 m的矩形光滑巷道，风门开合程度为50%（形成的障碍物高度H＝2．1 m），进口风速Vinlet分别为1、2、4、6 m／s，超出安全规程的8，10，12 m／s用于对照，风流方向沿X轴正向。不同进口风速下风速比（V／Vinlet）随风门后距离的变化如图6所示。从图6可以看出，迎风面（X＜0 m）处风速比并无明显变化，在X＝0～10 m范围内波峰为风门后形成的空腔区，空腔区内风速点距离随着进口风速增大而稍有增大，其中10 m／s和12 m／s处最为明显；30 m处风速值衰减比例分别为64．0%和55．5%，40 m处风速值衰减比例分别为84．6%和81．0%，可见进口风速主要影响背风面风速分布，且随来流风速增大，风门作为障碍物的影响作用加强，空腔区范围及衰减比例增大。处在矿山安全规程范围内的模拟风速（1～6 m／s），其风速增大对背风面风速影响不明显，30 m处衰减比例分别为70．3%、69．5%、69．0%和68．7%，40 m处衰减比例分别为87．4%、87．0%、86．8%和86．5%，可见进口风速1～6 m／s时，来流风速大小对于风门后风速分布无明显影响，这与文献［7］对于不同通风风速影响的研究结果一致。

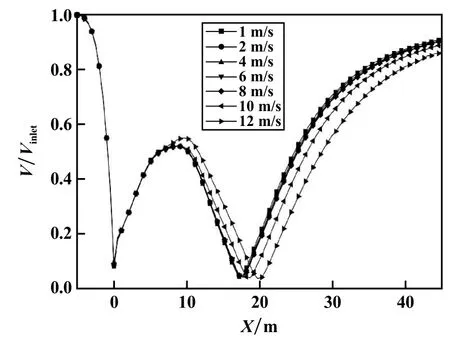
图6 不同进口风速时沿巷道中心线3 m处的风速比

3．2 风门开合程度的影响

根据风门开合程度建立不同尺寸的几何模型，使L1＝－10H、L2＝40H。选取开合程度为10%、30%、50%、70%、90%，则H分别为3．18、2．54、1．90、1．26和0．62 m，建立5种长度的光滑巷道模型，断面尺寸4 m×3．5 m，进口风速2 m／s，来流方向沿X轴正向，巷道中心线Y＝3 m处不同风门开合程度下风速比与距高比之间的关系如图7所示。改变风门开合程度后，迎风面风速比未发生较大变化，背风面变化则较为明显，开合程度越小（障碍物高度越高），空腔区风速比越大；虽然不同开合程度之间风速比差距明显，但空腔区水平分布稳定在6H～9H范围内，超过这一范围可避免空腔区涡流的影响；在进入尾流区后，风流开始抬升，以10%和30%处最为明显，因为此时巷道上下压力差最大；以进口风速90%作为评估标准，达到这一标准的距高比分别为15H、17H、22H、35H，开口程度90%时距高比40H处的衰减比例为79．8%。

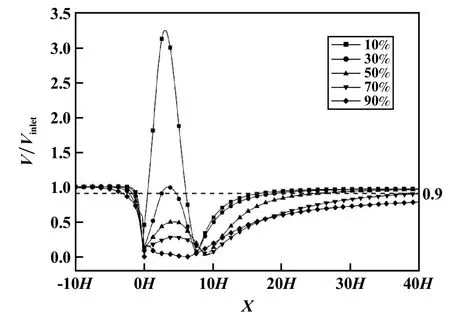
图7 不同开合程度下沿巷道中心线3 m高度处的风速比

提取开合程度10%、50%、90%的模型在Z＝0平面上的数据，进一步考察开合程度的影响。以虚线表示障碍物高度H，不同位置巷道断面垂直风速廓线分布如图8所示。以X＝－5H所在速度廓线为进口风速、X＝－0．5H处所在速度廓线为迎风面风速，X＝5H、10H、20H、30H为背风面风速。其中X＝－0．5H、5H、10H处的风速廓线与进口差异明显，X＝－0．5H处的风流由于风门的阻碍切分作用，风速廓线分布开始出现偏差；在抵达背风面后，5H处受空腔区影响，风速比先增大后减小再增大，最小值所在位置即为空腔区中心；从X＝10H开始，风流绕过空腔区，受压力差作用开始抬升，并在20H、30H处逐渐恢复至来流状态；空腔区对背风面风速分布的影响在距顶壁约为2H范围内，但因巷道高度有限，风门开合程度减至50%（H＝1．9 m）时，便可对整个巷道垂直方向的风速分布造成影响。

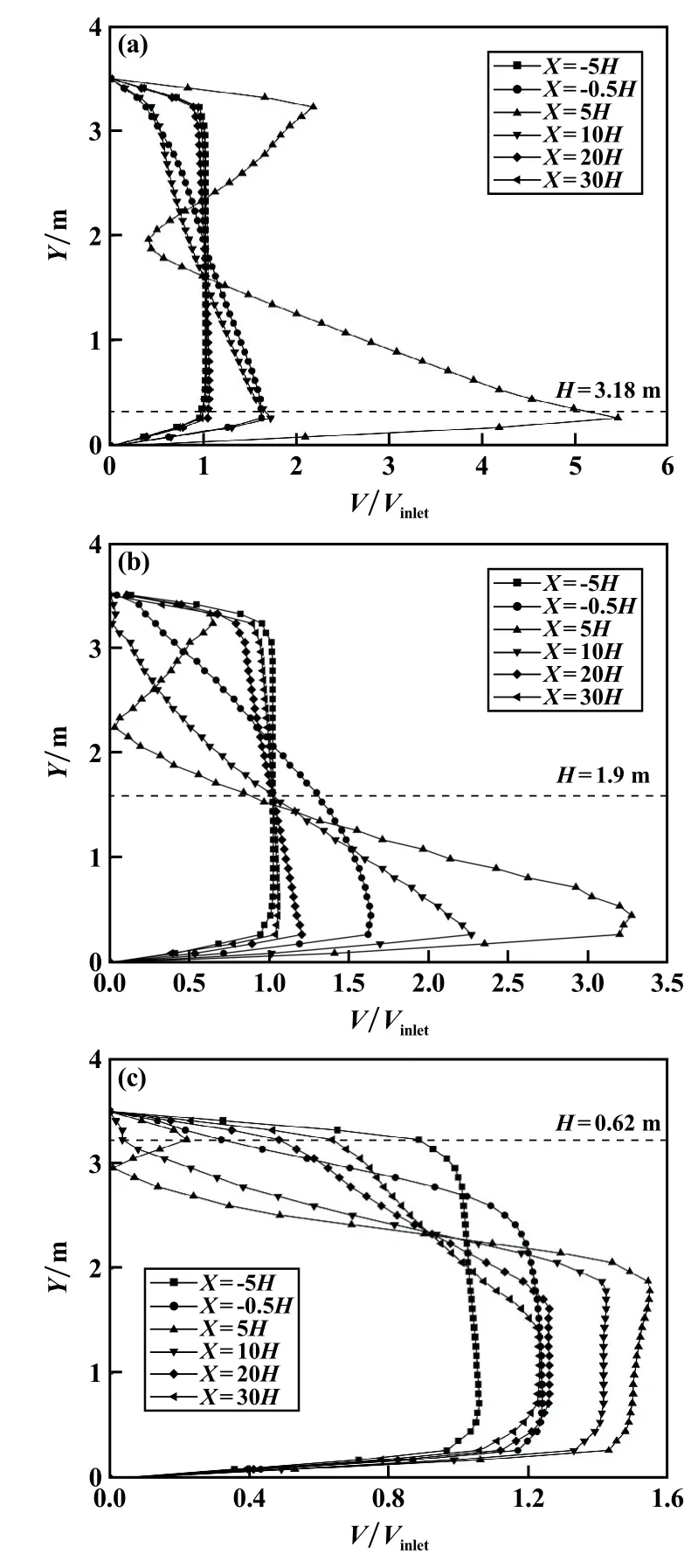
图8 Z＝0上不同X位置处巷道垂直方向风速比

3．3 顶壁粗糙度的影响

选取不同粗糙度R作为风门后长L2的顶壁模拟粗糙度，风门前长为L1的巷道壁面光滑。考虑到当前置障碍物高度对R的影响［16］，设置风门开口程度为90%（H＝0．62 m），建立矩形巷道模型，断面尺寸4 m×3．5 m，巷道长度80 m（L1＝20 m，L2＝60 m），进口风速4 m／s，风流沿X轴正向。不同R值下Y＝3 m处沿巷道方向的风速如图9所示。以R＝0 m处风速大小为标准值，在X＝10～20 m处，风速值差异较小，X＝20 m之后，R对巷道风速存在明显影响，且同一高度下R越大，风速值与标准值偏差越大，但风速总体变化与光滑壁面类似，呈波动上升趋势。

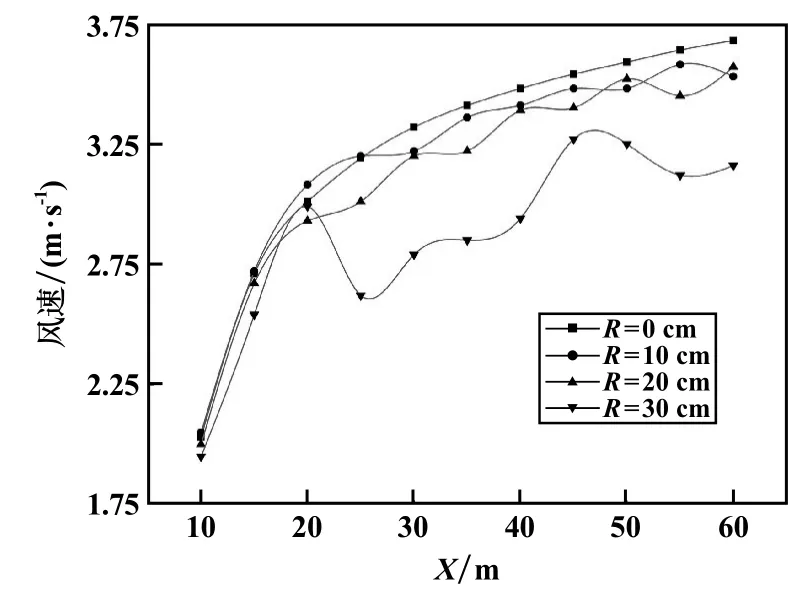
图9 Y＝3 m处不同粗糙度壁面沿巷道方向风速分布

不同R值的模型在Z＝0平面上的速度分布如图10所示。可见，风门后流场与理论基本一致，存在空腔区、尾流区；增大R对风门后高速区域范围无明显影响，低速区域则由于粗糙元的高度和分布不同有所差异；随着风流逐渐远离风门，沿巷道方向的上部风流出现分层，且这一现象随R增大越发明显，这是因为随着R增大，巷道顶壁阻碍能力加强，一方面风流绕过粗糙元提供了一部分位移厚度，另一方面由于黏性阻滞，靠近顶壁附近的风流对下部风流的摩擦使得风速出现分层。可见在粗糙壁面下，不同高度巷道风速大小确实存在明显差异。

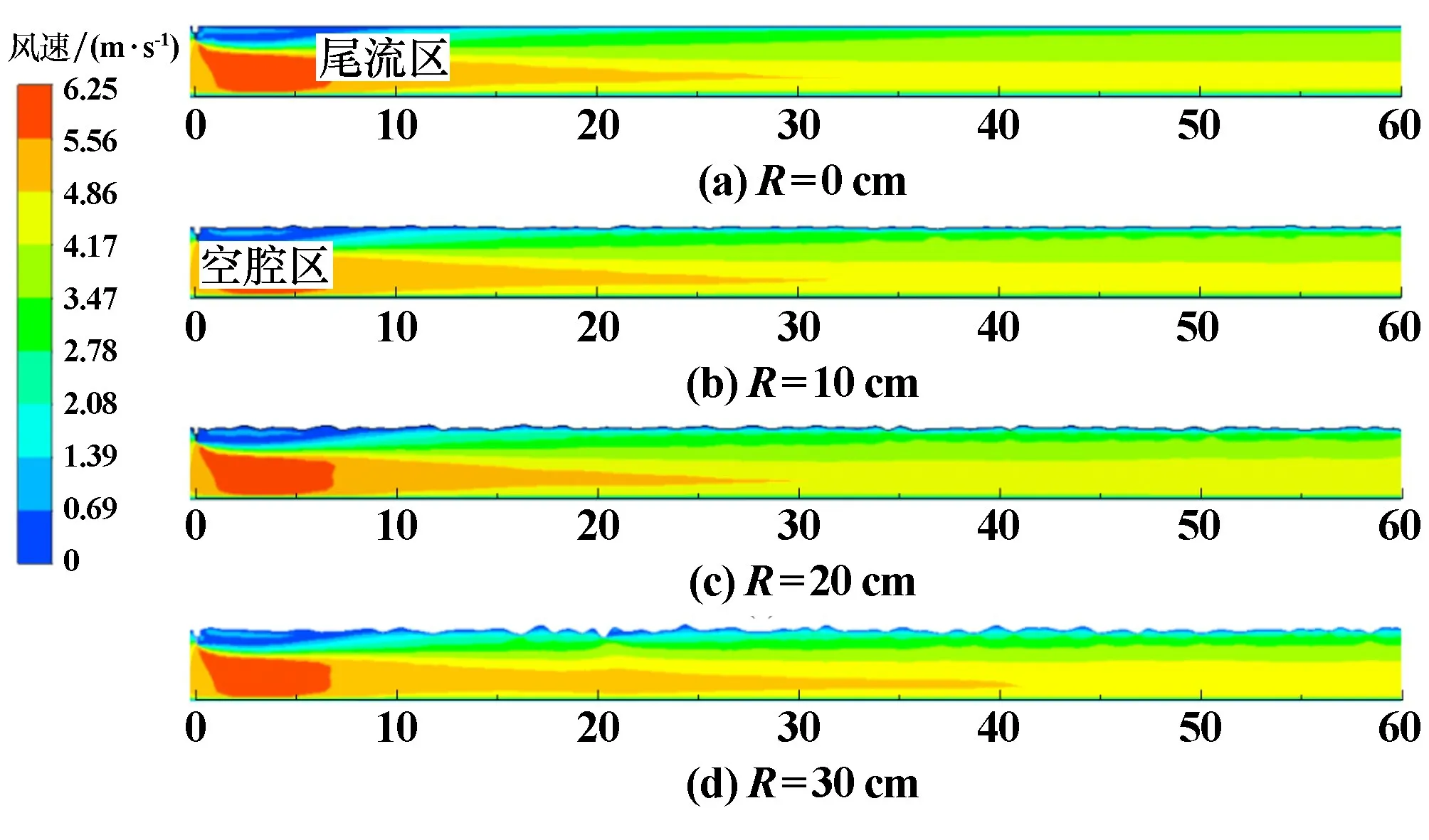
图10 风门后Z＝0平面不同粗糙度风速分布云图

提取不同粗糙度模型在X＝20～60 m的模拟数据，不同R值下平均风速及平均衰减比例如表1所示。可知，随着Y值减小，平均风速值及平均衰减比例呈上升趋势，通过降低传感器布置高度，可以远离粗糙顶壁的影响，增强风速监测的准确性。但考虑到实际工程中，巷道内存在人员、车辆的移动，传感器仍需保持一定的悬挂高度，故以达到光滑壁面风速90%作为评估标准。可见，保持距粗糙顶壁2R的距离进行测量可以较好地避免粗糙壁面的影响，提高风速测量精度。

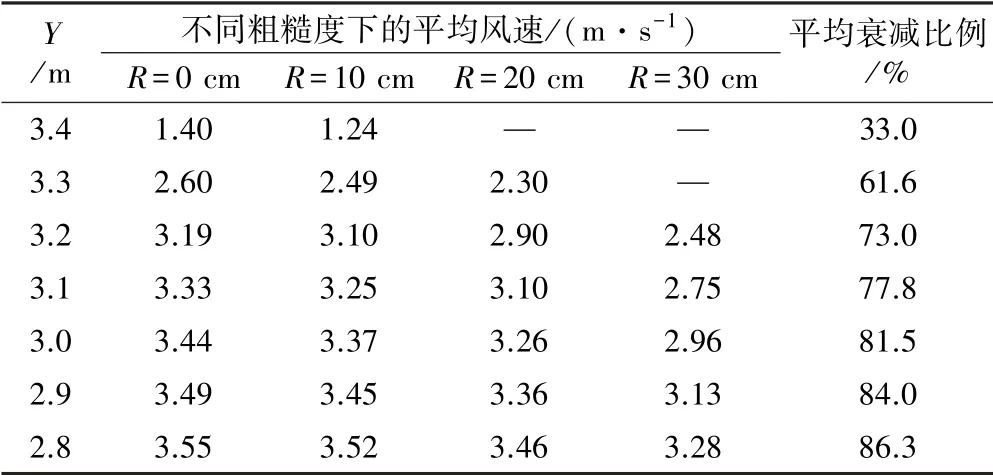
表1 Z＝0平面内不同高度平均风速及平均衰减比例

4 结 论

1）根据模拟结果，风门后的流场结构与理论相一致，存在空腔区和尾流区。其中，空腔区的水平影响范围约9H，竖直影响范围约2H。

2）处在井巷安全规程范围内风速（1～6 m／s）改变对巷道风速分布影响不明显；风门开合程度对风速分布的影响主要通过空腔区来体现，开合程度越小，空腔区风速比越大；粗糙顶壁加强了沿巷道方向风速值的波动，使得巷道上部风流出现分层现象。

3）根据开合程度，传感器的水平位置距风门距离大于9H时，可摆脱空腔区影响，距离大于35H时，可使测量风速达到进口风速约90%水平；根据顶壁的粗糙程度，传感器竖直位置距顶壁距离大于2R时，可使测量风速达到标准值90%。