板式相变储能换热器的性能优化

刘丽辉，张 航，彭子安，李 杰，孙小琴

（长沙理工大学能源与动力工程学院，湖南 长沙 410004）

近年来，我国越来越重视可再生能源的开发和应用，根据国家电网提供最新数据显示，截至2019年，煤炭占比为57.7%，较2010年下降11.5个百分点；太阳能、风能等非化石能源占比为15.3%，呈现上升态势。但由于可再生能源的间歇性、能级跨度大、应用稳定性差等特点，发展可持续的能源生产和消费方式，仍然是人类社会发展面临的重大挑战之一。储能技术因其可以协调能源供需间匹配、实现可再生能源的有效分配和利用日益引起各国的关注。相变储能技术具有储能密度大、储能规模适中、便于热控等特点，使其成为储能技术领域的重点研究对象[1]，在太阳能、风能发电，工业余热回收利用，分布式能源系统等领域具有广泛应用[2]。

相变储能技术的实现需要依赖储能系统完成，常见的相变储能系统的封装结构可以分为三种：圆柱形储能单元、管壳式储能单元以及矩形储能单元[3-4]，国内外对不同的封装形状做了大量的对比分析。VYSHAK等[5]发现在相同条件下，矩形单元结构中相变材料的熔化速率明显优于圆柱形结构，管壳式结构中的熔化时间更短。李洋等[6]定量比较了管壳式和板式相变换热的二维熔化模型，结果发现管壳式与板式换热器分别需要6 h、8.5 h完全熔化，主要是由于二者在换热管/板在排布上差异导致，相较于管壳式换热器，板式换热器结构紧凑、加工工艺简单、拆卸简便，比较两者的综合性能时发现板式换热器具有更大的发展潜力。尹点[7]设计了一种板片式换热器，通过非稳态储热模拟与实验对照的方法对换热器性能进行研究，并探究相变材料层以及热流层结构参数的变化对于相变材料相变过程的影响，发现改变相变材料层与热流层的厚度均对储能速率与储能量产生影响，且储能速率与储能量往往成反比，因此需要根据实际情况权衡储能速率与储能量的影响。另外，许多学者[8-9]在研究相变储能单元传热特性中发现，由浮力引起的自然对流在相变传热过程起着非常重要的作用。夏莉等[10]利用相变材料的储/放热实验台测试石蜡的储/放热性能，实验表明纯石蜡在储热过程中自然对流是其主要的换热方式，而放热过程中导热是主要的换热方式。自然对流增加储热过程的复杂性，因此相变储能过程的传热机制与性能优化仍然值得进一步研究与探索。

综上所述，平板式相变储能模块具有比表面积比较大、厚度方向导热性好、加工过程简单、组配灵活等优点，为后期维护提供了极大便利，目前在电子器件热管理、建筑节能、太阳能热利用等领域具有良好的应用前景。但受储能单元结构、相变过程自然对流及传热流体的影响，储能性能并不稳定。本文利用控制变量法，控制换热器的体积与储能量不变，构建了5种不同结构的板式相变储能换热器模型，利用FLUENT软件分别对其进行数值模拟，并研究不同结构与工况对板式相变换热器的储能特性及压降的影响。根据储能效率评价不同参数下换热器的性能，最终得出最优的换热器结构。

1 数理模型

1.1 问题描述与模拟方案

为了探究在一定空间内，换热器内部结构及不同工况对板式相变换热器性能的影响，本文设计了一种储能量为1800 kJ、宽高比为3∶1的板式相变储能换热器[11]，其具体尺寸如图1所示。为了简化模型设定热流通道厚度与相变单元厚度相同，图中热流(红色部分)为热空气，相变单元(蓝色部分)为熔点为27℃的石蜡。储能时，温度高于石蜡熔点的气流进入换热器与石蜡进行热量交换，石蜡吸收热空气的热能熔化，当石蜡完全熔化时，储能完毕。

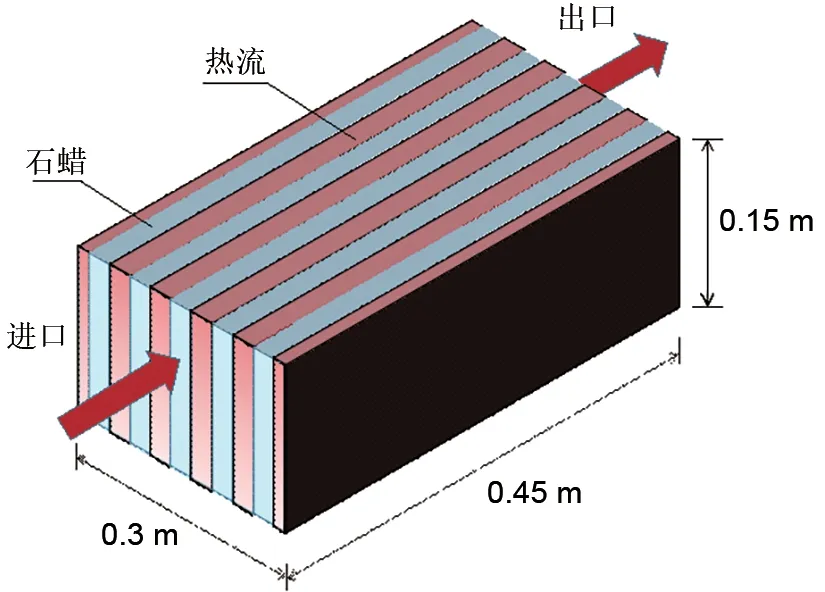
图1 板式相变储能换热器示意图Fig.1 Schematic diagram of plate-type phase change heat exchanger

在板式相变储能换热器的总体尺寸与总储能量一定的情况下，相变单元厚度越小，其表面积与体积之比则越大，在相同体积下相变材料与气流之间的热量传递越多。但由于减小厚度会增加换热器的制造及运行成本，为了权衡换热器储能速率与运行成本之间的关系，本文针对相变单元/气流通道厚度进行模拟研究。不同厚度的相变单元模拟方案见图2，图2为相变储能单元数量N为1、3、5、7、9时模型的截面图，不同相变储能单元数量N对应不同的单元厚度。本文模拟方案的具体参数见表1。

图2 不同相变单元数量的换热器截面示意图Fig.2 Cross section diagram of plate-type phase change heat exchanger with different number of phase change units

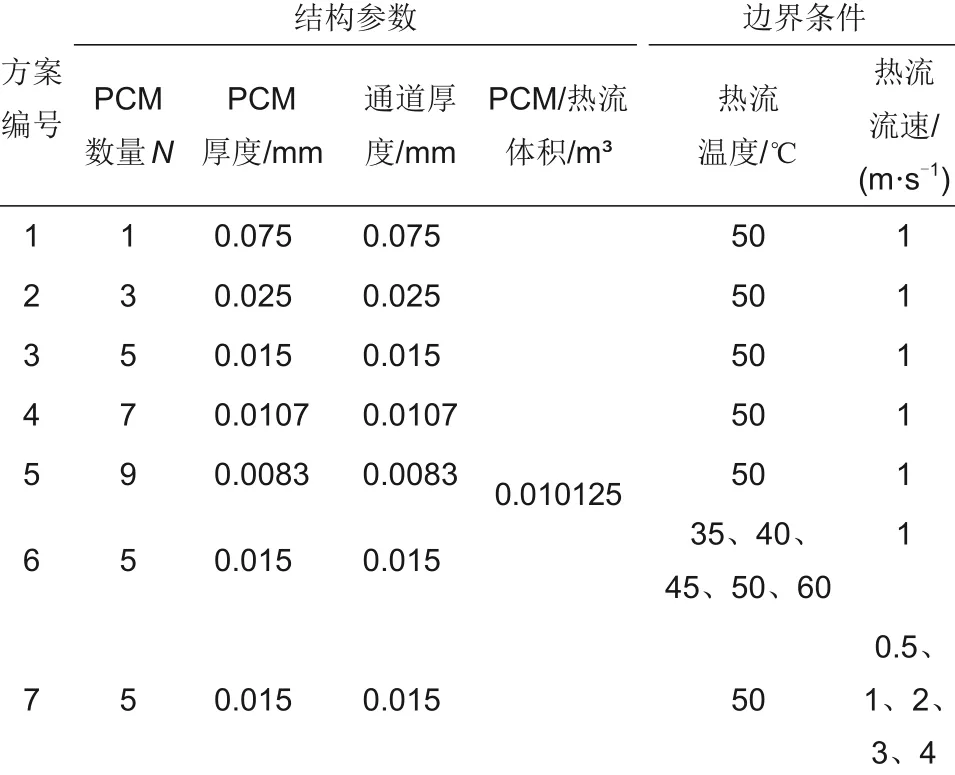
表1 模拟方案Table 1 Simulation case

1.2 物理模型

本研究利用FLUENT软件进行三维瞬态数值模拟，为了减少仿真时间与计算资源，对换热器进行了对称边界建模。以相变单元数量N=5的换热器模型为例，设置初始温度为25℃，边界条件的设定见表1，石蜡的物性参数表见表2。

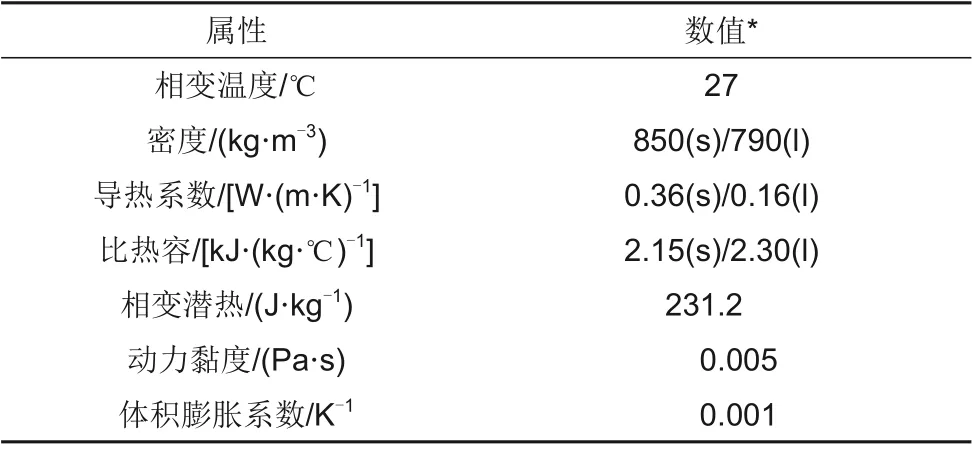
表2 石蜡的热物性参数Table 2 Thermophysical parameters of paraffin

1.3 数学模型

本文使用FLUENT软件中Solidification＆Melting模型对板式相变单元的蓄热过程进行模拟，该模型是采用Valler和Brent等[12]提出的焓-孔隙度技术[13]对固液界面进行跟踪，专门用于求解具有相变过程的流动换热问题。假设相变温度范围是Ts～Tl，液相率Φ由以下关系式定义

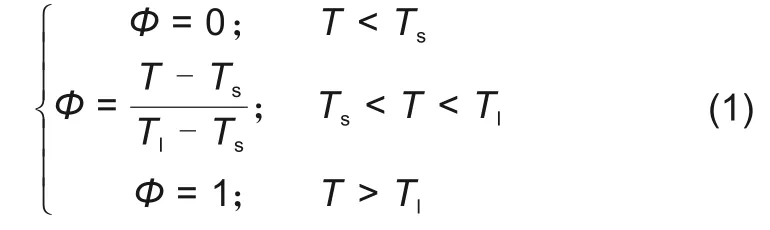
考虑到相变传热过程的复杂性，为了简化计算，做出如下假设：①流动是层流和牛顿流体，不存在黏性耗散；②相变材料石蜡均为均匀各向同性；③忽略管壁厚度和内壁热阻；④糊状区域的密度变化是温度的线性函数；⑤忽略相变材料石蜡由固液两相状态变化引起的体积变化；⑥由于相变过程中相变材料的密度变化会形成自然对流，相变材料的密度使用Boussinesq假设。基于上述假设，控制方程为

连续性方程

动量方程

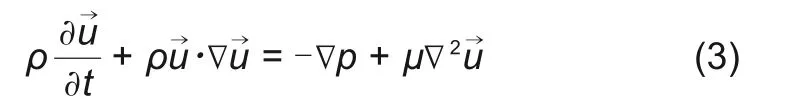
能量方程

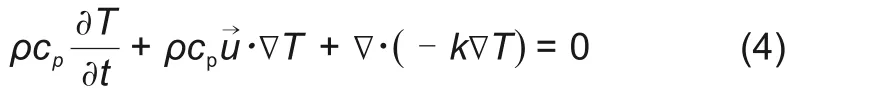
其中，ρ为密度；p为压强；T为温度；u→为速度矢量；cp为比热容；k为导热系数；μ为动态黏度。

2 模型验证

2.1 网格与步长独立性验证

网格形式采用非均匀的六面体网格，对传热壁面边界层的网格进行了加密以提高计算精度。为了验证网格的独立性，分别对不同网格数量进行求解计算，以N=5模型为例，计算熔化时间为10000 s时的液相分数结果见表3。当网格数量为81900时，液相分数仅比下一个模拟值少了0.1%，因此为了节省计算资源，可选择网格数81900进行计算。

表3 网格独立性验证Table 3 Grid independence verification

为了检验时间步长设置对实验结果的影响，设置了3种不同时间步长进行计算，各时间步长的计算结果如图3所示，可以看到时间步长的设置对模拟结果的影响较小，步长为10 s与50 s的平均误差约为2.2%，最终选择时间步长为20 s进行计算。

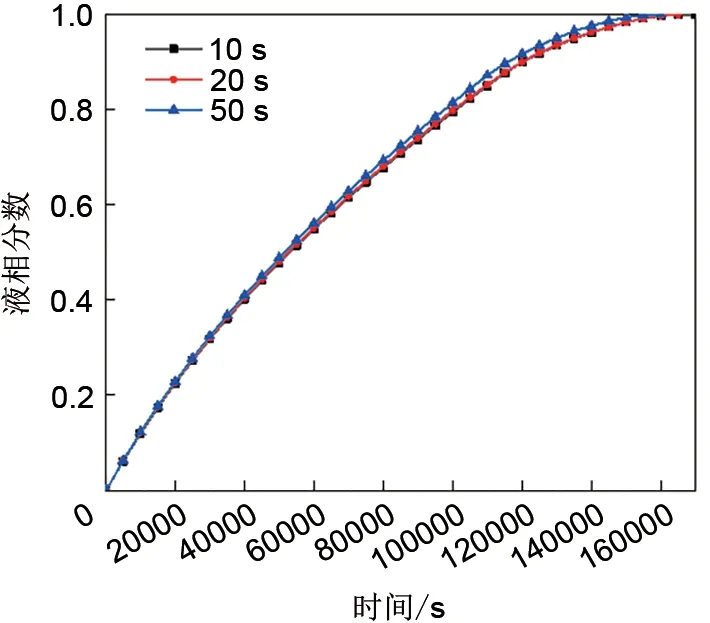
图3 步长独立性验证Fig.3 Step independence verification

2.2 模型验证

为了验证计算模型的有效性，对板式相变单元储能实验值[11]进行了仿真。本研究仿真了有无自然对流的两种模型，并对实验结果进行对比，图4为宽高比为3∶1的板式相变单元放置在50℃的环境中储能过程仿真与实验的液相分数。可以发现有自然对流的仿真与实验结果的液相分数曲线吻合良好，平均相对误差为2.28%。无自然对流(纯导热)的熔化过程慢于有自然对流，与实验的相对误差达到20%。实验与仿真对比结果表明，实验熔化过程中存在自然对流，且自然对流可加快石蜡熔化，因此进行模拟仿真时考虑自然对流是必要的。

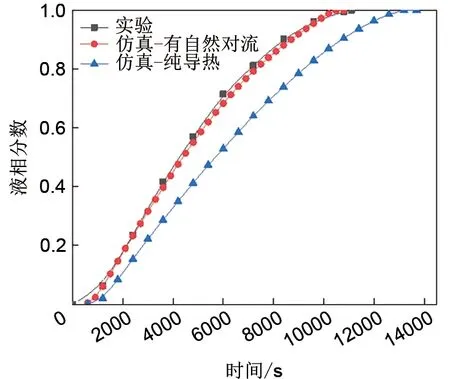
图4 实验与模拟液相分数的对比Fig.4 Comparison of experimental and simulated liquid fractions

3 结果与讨论

3.1 不同结构对换热器性能的影响

为了探究不同结构对换热器储能特性与压降的影响，采用控制变量法，控制进口热流温度均选取50℃，入口流速为1 m/s，通过改变板式相变储能换热器内部结构，对液相分数、压力场进行分析。

3.1.1 不同结构对储能特性的影响

图5所示为不同结构换热器在不同时刻下的液相率变化曲线，从图中可看出，换热器的内部结构对换热器储能过程影响较大。在相同的熔化时间内，N越大(厚度越小)，换热器中熔化完成的石蜡越多，即熔化速率与相变单元的厚度呈负相关。如在熔化10000 s时，N=9的换热器中的液相分数达到86.4%，而N=1的换热器中的液相率仅为8.7%。其主要原因为N越大，相变单元与热流的传热面积越大，携带相同热量的热流流过换热器时，在相同时间内能吸收更多的热量。因此换热器内部石蜡的总熔化速率增大，但增大的幅度逐渐减小，如N=7与N=9的完全熔化时间较接近，这是由于在增加相变储能单元数量的同时，热流通道的厚度也在减小，相同的换热面积流过的热流所携带的热量减小；此外，由于石蜡的导热系数较低，在单位时间内储存热量能力有限，因此也限制了熔化速率的提升。

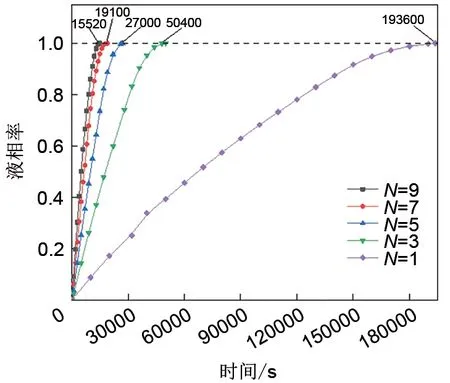
图5 不同结构换热器的液相率Fig.5 Liquid fraction of plate-type phase change heat exchanger with different structures

3.1.2 不同结构对压降的影响

不同结构的板式相变储能换热器热流进出口压降如图6所示，压降随着相变储能单元数量的增加而呈现指数上升趋势。说明减小热流通道的厚度会产生更大的压降，实际应用当中需要安装更大功率的风机来克服压降阻力损失。因此对于板式换热器的内部结构设计，不仅要考虑换热效果还要考虑压降损失，节约运行费用。

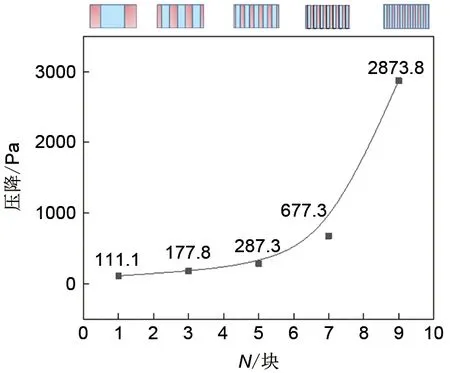
图6 不同结构换热器中的压降Fig.6 Pressure drop in plate-type phase change heat exchanger with different structures

3.1.3 不同结构对储能换热器性能因子的影响

模拟结果表明熔化速率随着N的增加而增加，但同时会增加换热器的压降损失，增加换热器的运行费用。因此在选择板式相变换热器的结构时需要综合考虑传热和压降的共同影响。为此，本文以单位时间储能量和压降评价板式相变储能换热器性能，见式(5)

其中，η为储能换热器性能因子，η越大，表示在储存相同热量的情况下耗电量越小，即运行费用越低；ΔPs为单位时间储能量，本文简称储能功率，计算式为式(6)；ΔPr为换热器单位时间克服阻力做的功，简称阻力功率，由式(7)计算

其中，Qt为换热器中PCM完全熔化时的总储能量，τ为换热器内PCM完全熔化需要的时长；Δp为换热器在单位体积流量下的压降；qv为单位体积流量。

图7为储能换热器性能因子η随相变单元数量增加的变化趋势。由图可知，单位时间内的储能量随着相变单元数量的增加而显著增大，但由于受到了压降阻力的制约，储能换热器性能因子η呈现先增大后减小的趋势。在本研究中N=5时储能换热器性能因子η达到最大。当N<5时，储能换热器性能因子η随N的增加而增大；当N>5时，η呈现下降趋势，且继续增加相变单元的数量N会进一步减小热流通道的横截面，导致阻力急剧增加，而储能速率的提升逐渐减弱，则η会随着N的增加而加速减小。分析结果表明，本研究在边界温度为50℃、热流流速为1 m/s时，相变单元数量N为5时为最佳板式相变换热器结构。

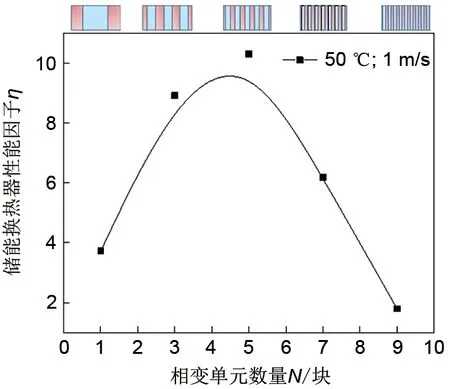
图7 储能换热器性能因子η随相变单元数量增加的变化Fig.7 Variation of heat storage exchanger performance factor"η"with increasing number of phase change units

3.2 边界条件对换热器性能的影响

3.2.1 边界温度对传热的影响

图8为不同热流温度下，相变储能换热器中石蜡液相率随时间的变化曲线。由图可知，储存相同的热量，若热流温度为35℃时需要75200 s，而热流温度为60℃时仅需19800 s。这是由于温度越高携带的热量越多，则单位时间传递给换热器中石蜡的热量越多，熔化速率越快。同理，当温度增加到一定程度时，继续增大热流温度对熔化速率的影响越来越小。另外，改变边界的温度并不会影响热流的流动方式，温度的改变不会影响换热器中压降的变化。因此在设计相变储能换热器时可以根据实际情况增加相变材料与边界环境的过热度，以加快储能速率。

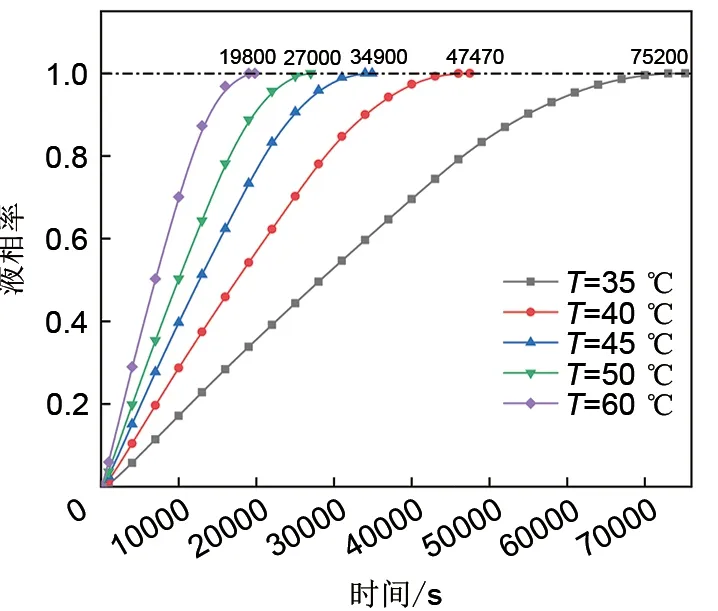
图8 不同热流温度的换热器的液相率曲线Fig.8 Liquid fraction of plate-type phase change heat exchanger with different heat transfer fluid temperature

3.2.2 入口流速对压降和传热性能的影响

3.2.2.1 入口流速对压降的影响

图9为压降随热流速度的变化曲线。入口的压力随着流速的增加而增加，且流速越大，通道中的压力梯度越大，即热流进出口压降越大，且增大呈现加快的趋势。这是由于流体存在黏滞性，阻力与流速成正比。因此在设计相变储能换热器时可以适当的增大边界流速来提高熔化速率，但过大的速率会增加风机的功耗。

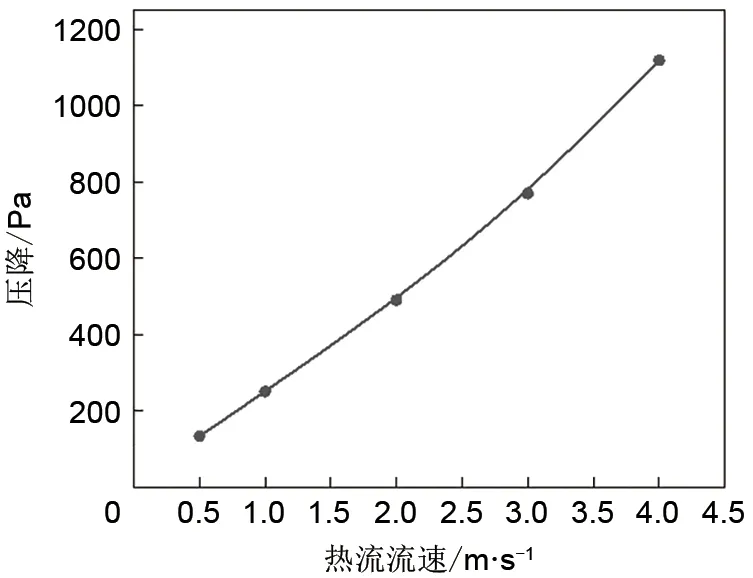
图9 压降随热流速度的变化曲线Fig.9 Pressure drop in plate-type phase change heat exchanger with different heat transfer fluid velocity

3.2.2.2 入口流速对传热性能的影响

图10为不同热流流速下相变储能换热器内石蜡的液相率曲线。在其他参数均相同的情况下，增大入口流速可以加快石蜡熔化。在相同的时间内流速越大，流入热通道的热空气越多，则传递给相变单元的热量也越多，所以石蜡熔化的越快。但熔化速度加快的效果会随流速的增大而减弱，这是因为石蜡的导热系数低，在相同换热面积下，单位时间的换热能力有限；且流速增加使得单位质量的热流在通道中停留的时间更短，单位质量热流的换热量减少。

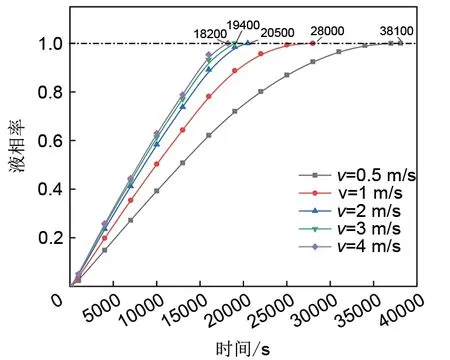
图10 不同热流流速下相变储能换热器内的液相率Fig.10 Liquid fraction in plate-type phase change heat exchanger under different heat transfer fluid velocity

图11为不同流速下换热器的出口平均温度，不同流速下的出口平均温度均呈现缓慢上升的趋势，这说明随着熔化的进行，单位质量热流与石蜡进行的热量交换逐渐减少，石蜡熔化速率缓慢降低。这是由于随着熔化的进行，靠近换热壁面的石蜡温度越来越高，与热流之间的温差逐渐减小，因此换热效果减弱。另外，从图中可知，出口平均温度与热流流速呈正相关，即流速越大，出口平均温度越大。这说明流速越小的相变储能换热器，单位质量流量的换热效果更好，且单位质量流量的换热效果随流速减小而增强。因此在设计相变储能换热器的换热流体流速时，不仅要考虑储能速率，还要考虑压降损失与单位质量流量的换热效果。

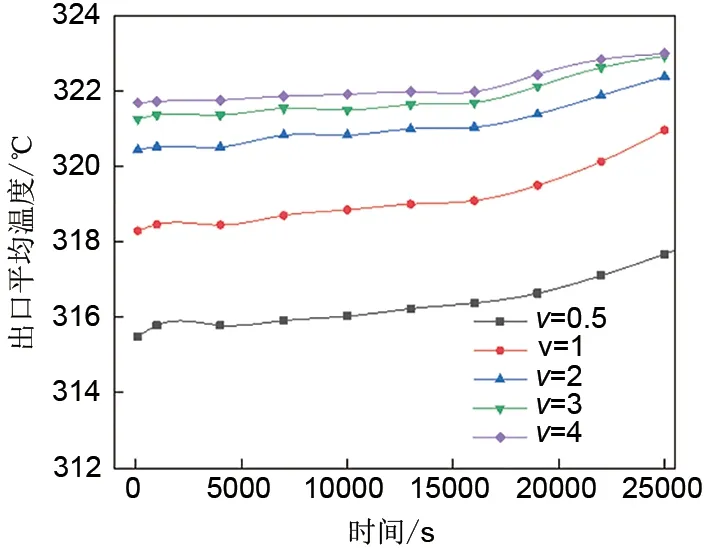
图11 不同流速下换热器的出口平均温度Fig.11 Average outlet temperature of plate-type phase change heat exchanger under different heat transfer fluid velocity

3.2.2.3 入口流速对储能换热器性能因子的影响

图12为不同结构的相变换热器在不同热流流速下储能换热器性能因子η的变化情况。在不同的热流流速下，储能换热器性能因子η随相变储能单元数量N的变化趋势不变，均为随着N先增大后减小。但热流流速对储能换热器性能因子η的大小有着重要的影响。当流速增大时，不同结构的储能换热器的储能换热器性能因子η均降低，但降低的幅度逐渐减小。这是因为增加流速不仅增加了换热器的压降，同时加快了相变材料的熔化进程，从而减小了储能换热器性能因子η。另外，不同的热流流速对不同换热器结构的影响呈现差异，如当流速为0.5 m/s时，N=5的换热器的储能换热器性能因子η比N=9的大25，而当流速为2 m/s时，N=5的换热器的储能换热器性能因子η比N=9的仅大2。因此流速越小，换热器内部结构对储能换热器性能因子η的影响越明显。本研究中换热器性能最佳为V=0.5 m/s，N=5的模型。在实际应用中当流速较小时，需要重点关注换热器内部结构的设计。

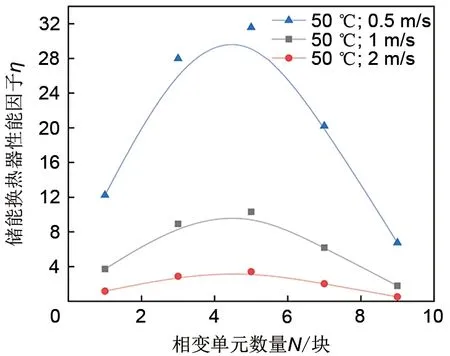
图12 不同结构的相变换热器在不同热流流速下的储能换热器性能因子ηFig.12 Heat storage exchanger performance factor"η"of plate-type phase change heat exchanger with different structuresunder different heat transfer fluid velocity

4 结 论

本文设计了一种板式相变储能换热器，并且在控制该换热器的外形参数不变的情况下，设定了5种不同相变单元数量的换热器模型，通过数值模拟的方法探究不同相变单元厚度和传热流体变化对换热器性能的影响，结论如下。

（1）在相同换热器的体积下，板式相变单元数量的增加会加快储能速率，但同时会增加风机的阻力，因此储能换热器性能因子的大小随相变单元数量先增大后减小，综合考虑得到N=5为最佳相变单元数量。

（2）板式相变储能换热器的流体流速与储能速率成正比，与压降成反比，且单位质量的热流的换热效果随流速减小而增强。

（3）板式相变储能换热器的储能速率与热流温度成正比，但储能速率增加的幅度随着热流温度的增加而减小。

（4）本研究中换热器性能最佳为v=0.5 m/s，N=5的模型。在实际应用中当流速较小时，需要重点关注换热器内部结构的设计。