塞块量热计的热流计算与修正方法研究

朱新新, 王 辉, 杨 凯, 朱 涛, 杨庆涛, 刘进博

(中国空气动力研究与发展中心 超高速空气动力研究所, 四川 绵阳 621000)

0 引 言

地面防热试验是高超声速飞行器设计与考核的必要环节[1-2]。随着航天技术的飞速发展和高超声速飞行器精细化设计热考核需求的提升[3-4]，地面防热试验中对热流等测量参数的精准度要求越来越高[5]。在以电弧风洞为代表的地面防热试验设备的流场校测中，塞块量热计常被选作测量热流的主要传感器[6]。塞块量热计可分为空气隙结构和隔热套结构两类[7-8]，空气隙结构的装配工艺较难控制，更适合驻点热流测量；隔热套结构的工艺易于实现且不受流场条件限制。两种结构的热流计算均采用绝热假设的近似计算方法，这种近似计算会带来较大误差，国内外研究者力图对其进行优化和修正：

一方面，通过改进塞块量热计的隔热结构使其尽量满足绝热条件，如杨庆涛等[9]提出的尖楔状隔热套结构、许考等[10]提出的线接触隔热结构以及朱新新等[11]提出的中空隔热套封装结构，并给出了这种隔热套结构的相对优越性。即便如此，这些改进结构仍然未能达到较理想的绝热条件。

另一方面，是对热流计算方法进行修正。陈连忠[12]考虑到塞块热物性会随着温度的升高而改变，对其进行了一定程度的修正，降低了一部分计算误差。Mark Hightower等[13]考虑了空气隙结构下的热损失和变热物性两个因素，建立了一个近似的指数衰减理论模型，并基于该模型给出了修正公式，在一定程度上降低了热流测量误差。但正如文献[13]所述，将基于测试数据得到的热流修正参数代入仿真模型进行热流验证会存在一定偏差。出现偏差的原因有两方面：一方面，衰减理论模型中假定加热时隔热结构的温度始终不变，而实际情况是一直升高且不能忽略；另一方面，整个修正方法始终没有获得可溯源的热流真值，仅是一个基于流场测试数据的相对修正。有鉴于此，本文拟通过热流标定系统[14-15]获取可溯源的准确热流，并以此为依据建立塞块量热计的仿真模型，对热流测量结果进行计算修正。

1 塞块量热计的传热模型和热流计算方法

塞块量热计测量热流是基于能量守恒原理，假定塞块除受热面外，其余均为绝热面。但在实际研制和使用中，受材料和装配工艺等限制，很难达到理想绝热条件，热损失始终存在。为减少热损失，朱新新等[11]设计了一种中空型隔热套结构的塞块量热计，其结构如图1所示，从左上至右下依次为：耐热填充剂、封装壳、焊有热电偶的塞块、中空隔热套、螺钉。这种塞块量热计的优势在于塞块热损失较少且能将塞块量热计热流标定时内部的结构和热阻等传热特性保留到热流测量试验中。

图1 塞块量热计结构示意图

塞块量热计的传热模型如图2所示。其前表面为受热面，热流(qin)入射塞块后，塞块温度快速上升，可以通过测量塞块的温升率计算得到热流值。热流计算误差主要来自4个方面：一是塞块前端与耐热填充剂的热传导，热导率很低的耐热填充剂前端暴露于热环境中，局部温度会较高，表现为对塞块放热，但其后端温度较低，表现为对塞块吸热，总的表现为吸热(qcond1)；二是隔热套前端内侧面和后表面的内侧面对塞块的吸热(qcond2)；三是塞块对外热辐射带来的热损失(qrad)；四是塞块热物性发生了变化，若按常温时的热物性计算热流，会带来一定热损失(qvar)。

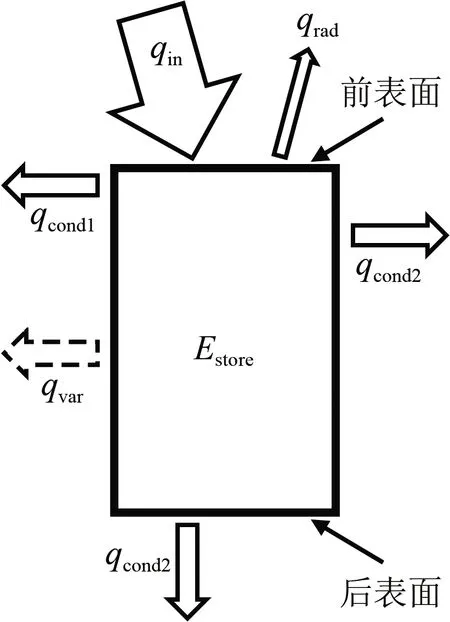
图2 塞块量热计的传热模型

假设图2中圆柱状塞块量热计的长度为l，横截面积为A，则根据能量守恒原理可得，任意时刻单位时间内的入射热能等于储存至塞块里的热能与损失热能之和：

qinA=Estore+Eloss

(1)

在某时刻t，塞块储存的热能Estore可根据其温升率计算得出：

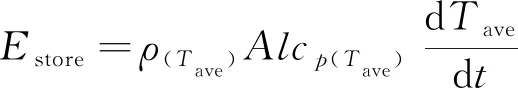
(2)

其中，Tave为塞块平均温度，ρ(Tave)和cp(Tave)为塞块在Tave时的密度和质量定压热容。式(2)取实时温度下的热物性，不会产生如图2所示的热损失qvar。则总的热损失包括前文所述的热传导损失和辐射热损失：

Eloss=qradS+qcond1S1+qcond2S2

(3)

其中，S为塞块表面积，S1为塞块与填充剂的接触面积，S2为塞块与隔热套的接触面积。由于塞块体积和长度很小，且具有较高的热导率，则有以下近似关系成立：

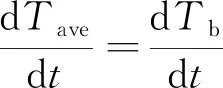
(4)

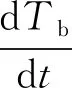
再设接触面上耐热填充剂的某接触位置z的接触热阻为Rcond1(z)，温度为T1(t,z)，则由接触热阻定义可推导出t时刻该接触面上的平均热流qcond1，同理可得qcond2：

(5)

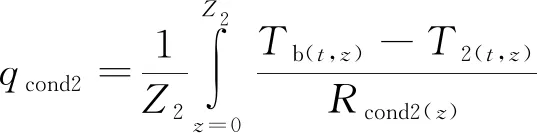
(6)

其中，Z1为塞块和填充剂的接触面长度，Z2为塞块和隔热套的接触面长度，Tb(t,z)取塞块后表面的测点温度Tb(t)。

另外，塞块量热计测量热流属于瞬态测量，塞块温度并不会很高(一般不超过600 K)，其辐射损失的热能与入射热能相差至少5个数量级，所以辐射热损失可以忽略。综合式(1)～(6)，可得塞块量热计的热流计算模型如下：

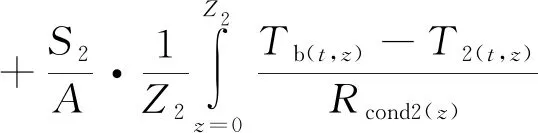
(7)

假设隔热结构完全绝热(Rcond1(z)和Rcond2(z)无穷大)，且塞块温升较小(热物性变化小)，则可得到常用的简化公式(8)：

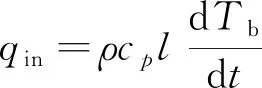
(8)

其中，ρ、cp为常温时的塞块密度和质量定压热容。

事实上，由于忽略了较多的热损失(这在后文的仿真计算和标定试验中会进一步说明)，这种假设对于隔热套结构的塞块量热计很难成立，按照式(8)计算热流会产生较大误差；而由于无法获得塞块与填充剂和隔热套之间的热流qcond1和qcond2，采用直接解析计算方法求解qin相当困难。因此，本文将基于热流标定系统和塞块量热计仿真模型对塞块量热计的热流测量结果进行计算和修正。

2 塞块量热计的仿真模型和影响因素分析

依据图1的塞块量热计结构建立如图3所示的塞块量热计轴对称仿真模型。塞块直径为4 mm，长度为7 mm。在图3中，上表面为热流加载面，除了8个不同材料间的接触面(图中编号1～8)，其余边界面设为绝热条件。整个仿真模型建立的难点是8个接触面热阻值的设置，因此，首先需要分析各个接触热阻对热流测量结果的影响。

塞块量热计包括4种材料：无氧铜(塞块和封装壳)、氧化铝(填充剂)、玻璃钢(隔热套)和螺钉(不锈钢)，根据查表后拟合得到的温度函数设置各材料的热物性参数。接触热阻主要跟表面粗糙度和受力情况有关，一般受力越大、接触面越光滑，接触热阻越小。接触面1和4的受力情况与材料均相同，其接触热阻相同，定义为R1,4；接触面2和3材料相同，且两个接触面受力都控制为较小力(为减小热损失)，也可定义接触热阻为同值，以R2,3表示；接触面6尽管材料与接触面2和3一样，但其装配时受紧固螺钉挤压，受力明显大于后两者，故将其定义为R6；接触面5、7和8的热阻分别定义为R5、R7和R8。

结合各接触面热阻特点，参考文献[16]对接触热阻的研究，对各接触热阻值作表1所示的定义和说明。

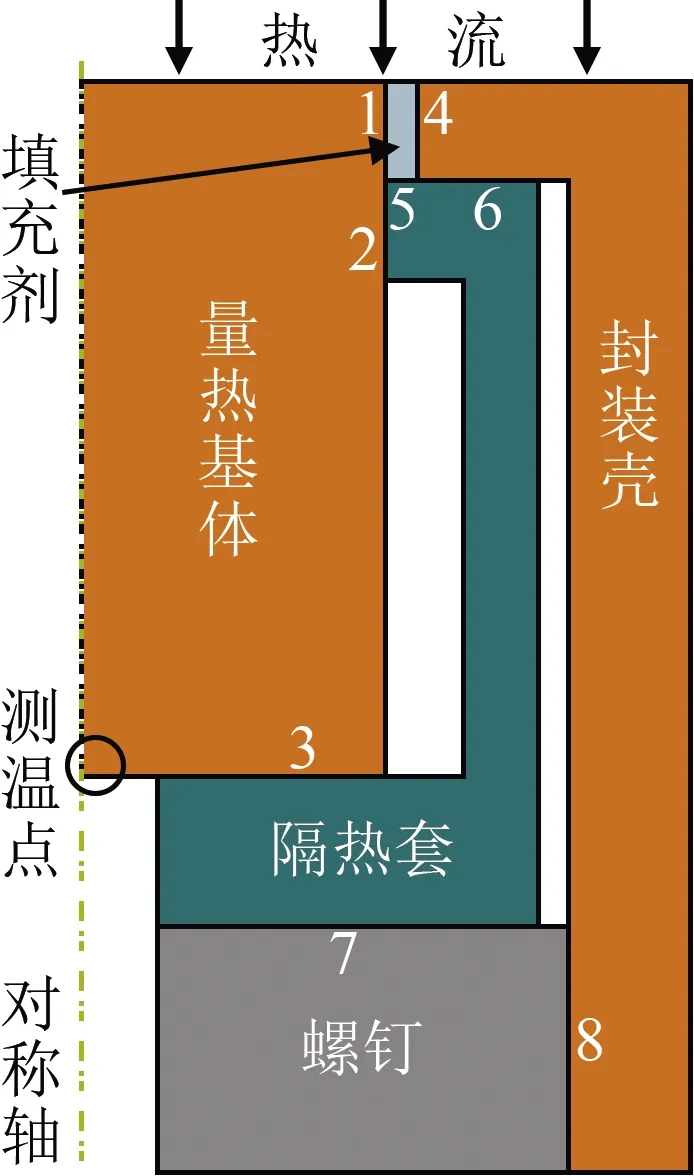
图3 塞块式量热计的仿真模型

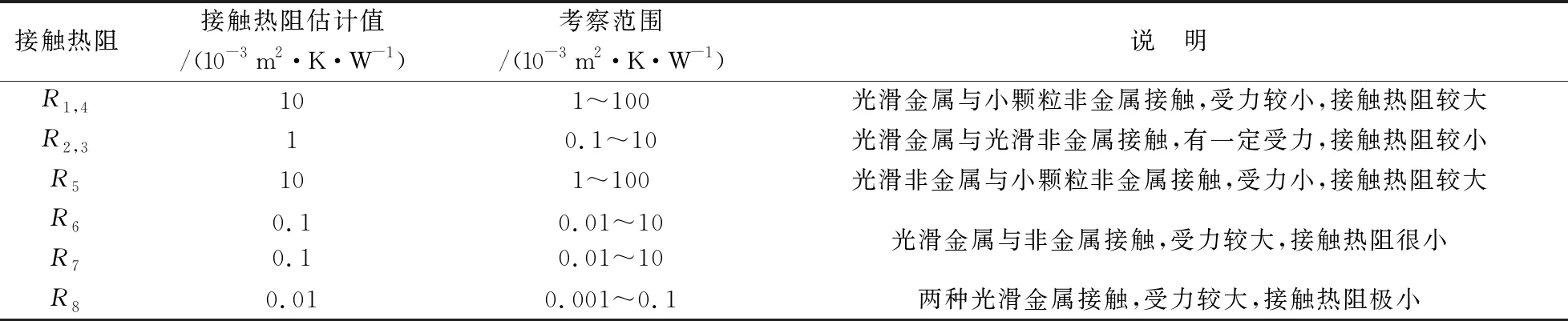
表1 不同接触面的热阻值Table 1 Thermal resistance of different contact surfaces

按表中第二列接触热阻估计值设定塞块量热计各接触面的热阻。不失一般性，设入射热流qstd为1 MW/m2，加热时间3 s，加热前所有部件温度初始值设为300 K。通过仿真计算，可以得到塞块后表面温度(Tb)、填充剂中靠近接触面位置的平均温度(T1)、隔热套中靠近接触面位置的平均温度(T2)的温升曲线，如图4所示。随着测试时间推移，塞块温升最快、填充剂其次、隔热套最慢，必然导致塞块与填充剂、塞块与隔热套的温差持续升高，其结果就是：在被测热流不变的前提下，测试时间越长，热损失越多，在测试时间段内提取温升数据的时间越晚，计算得到的热流误差就越大。

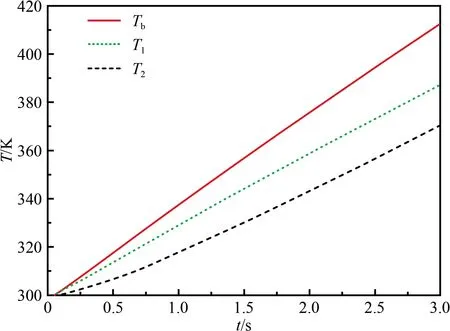
图4 塞块式量热计不同部位的温升曲线

为定量描述误差大小，定义一个计算误差ε：

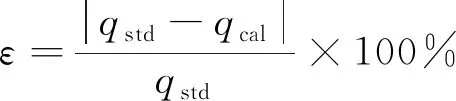
(9)

其中，qcal为采用式(8)计算得到的热流。

将图4中塞块的温升数据进行分段拟合，将拟合得到的温升率分别代入式(8)计算热流。如表2所示，在测试时间段内提取温升数据的时间越晚、测得热流越低，误差越大。即使进行了热物性修正(表2最后一列)，也仅稍有改善，这也进一步验证了式(7)中热损失的存在和不可忽略性。因此，在标定试验和实际热流测量中应尽可能早地提取温升数据。本文结合送进系统到达指定位置的时间(0.20 s)和塞块量热计的响应时间(0.25 s)，统一设定提取时间为0.5～0.7 s。

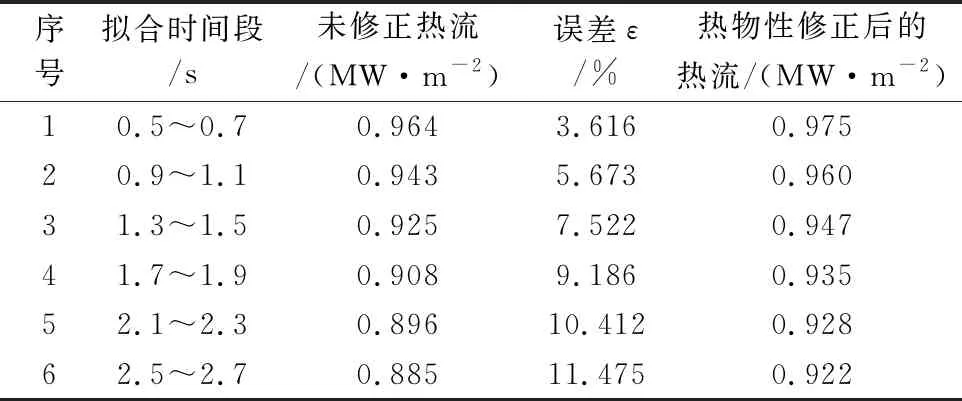
表2 不同时间段的热流及误差Table 2 The heat flux and error in different time periods

为分析接触热阻对热流测量结果的影响，表3给出了各个接触热阻单独变化时引起的计算误差变化情况。由表3可知，当接触热阻缩小或放大1个数量级时，对计算误差影响最大的是R2,3(塞块与隔热套之间的接触热阻)，其余5种接触热阻的变化对计算误差影响很小。这是因为与塞块直接接触的仅有填充剂和隔热套，而塞块与填充剂的接触面积小于塞块与隔热套的接触面积，且塞块与填充剂的温差也小于塞块与隔热套的温差(见图4)，因此，R2,3对塞块温升率的影响最大，即整个塞块量热计仿真模型对接触热阻R2,3的值比较敏感，需精确设置。

表3 不同热阻下的计算误差Table 3 Calculation error under different thermal resistance condition

3 塞块量热计热流计算的修正方法

塞块量热计的结构尺寸确定后，每加载一个不同的热流qin，都会在固定时间段内输出唯一的dTb/dt。将式(7)变形为：

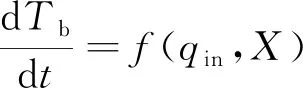
(10)

其中，X表示某具体传感器的固有属性，可视作一未知常量。基于式(10)，就可以在使用塞块量热计之前，先在一个热流已知的热源系统中对其进行标定，获得不同热流下对应的dTb/dt。在塞块量热计仿真模型中加载不同热流(如表4所示，其他边界条件和初始值与图4的仿真情况相同)，可得到对应的dTb/dt和热流计算误差。

表4 不同热流下的计算误差Table 4 Calculation error with different heat flux

仿真结果显示，加载热流越大，计算误差也越大；但这种增大趋势并非严格线性，这就给修正带来一定困难。比较极端的做法是标定足够多的试验数据，甚至做成一张热流分度表的形式，测试时通过温升率查热流分度表直接获得对应热流。但这并不现实：一方面，试验中使用塞块量热计的数量较大，且不同塞块量热计的固有属性X也不同；另一方面，会花费大量时间和成本在热流标定环节上，且目前热流标定系统的热流范围还比较窄，并未完全覆盖测试区间。基于此，结合设备实际及应用需求，提供两种方法：一种是直接比对标定修正方法；另一种是基于标定的数值计算修正方法。

3.1 直接比对标定修正方法

通过进一步开展仿真和标定试验发现，在较小的热流区间内，不同的加载热流引起的计算误差差异很小。因此，可以在一定热流测量区间内均匀选取n个(n≥3)不同大小的热流状态，在每个热流状态下用标准热流计测量得到参考热流qstd，将其值作为纵轴，将同样热流状态下由式(8)计算得到的塞块量热计热流qcal的值作为横轴，然后进行线性拟合，可得到该塞块量热计的标定曲线：

qstd=a+bqcal

(11)

其中，a和b为修正参数。在热流测量中，就可以用获得的修正参数a和b对计算热流进行修正，得到修正热流如下：

qcor=a+bqcal

(12)

需要说明的是，式(11)和(12)中的qcal不同。式(11)中的qcal是标定试验中的计算热流，其对应的真实入射热流(qstd)是已知的，用于求解修正参数a和b；而式(12)中的qcal是测量试验中计算得到的热流，其对应的真实入射热流未知，需要通过式(12)修正得到。

为评估上述修正方法的有效性，定义一个修正误差ε′，用于定量评估修正后的误差。

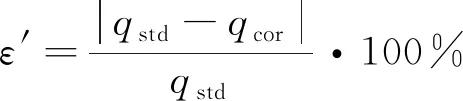
(13)

研制加工了5个塞块量热计(结构如图1所示)。图5为1#塞块量热计在5个不同热流下获得的标定曲线，其线性度极好(R2=0.9999)，通过线性拟合得到其修正参数a和b分别为-0.039和1.068。表5给出了1#塞块量热计的标定结果，包括5个标定状态及每个状态对应的计算误差和修正误差。

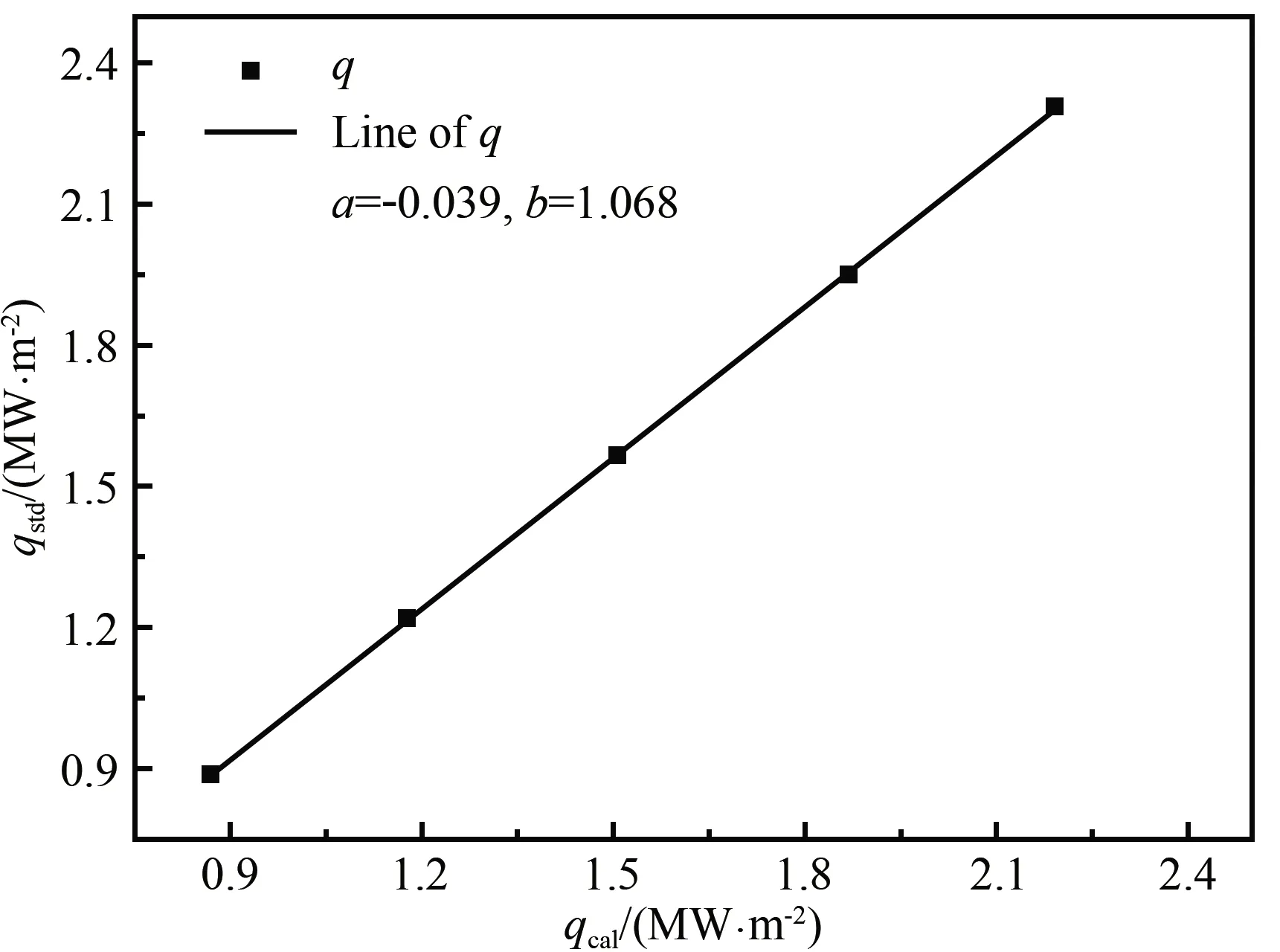
图5 塞块量热计的热流标定曲线

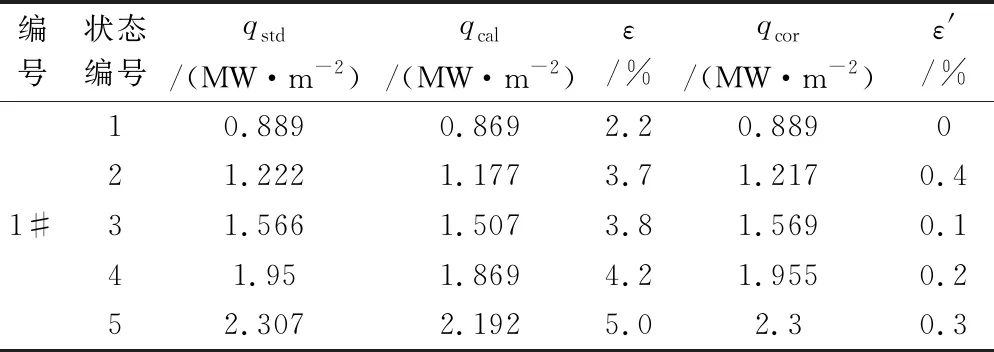
表5 不同状态修正前后的误差对比

表6给出了5个塞块量热计的标定曲线参数和对应的最大误差。由表6的标定结果可知，直接比对标定修正方法能够有效减小塞块量热计的热流计算误差，5个塞块量热计修正前的误差为5.0%～8.9%，修正后的误差降为0.4%～1.7%。

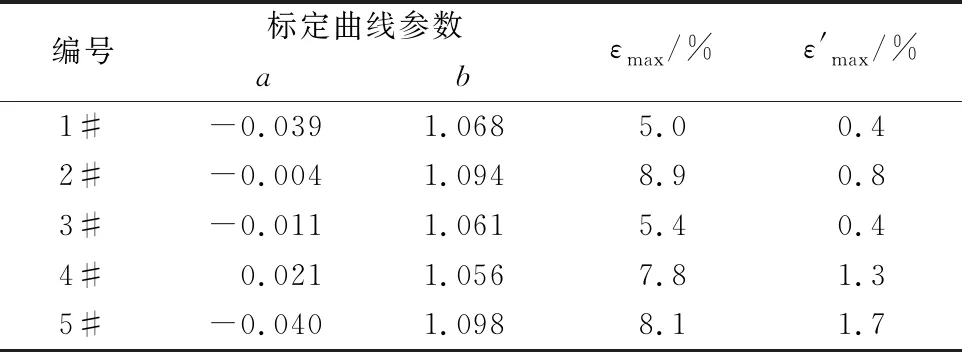
表6 不同塞块量热计修正前后的误差对比

3.2 基于标定的数值计算修正方法

对于热流标定系统不能覆盖的较高或较低的热流区间，拟借助求解塞块量热计仿真模型的途径进行修正。如前文所述，塞块量热计仿真模型是否准确主要受接触热阻R2,3影响，因此，求解塞块量热计仿真模型主要就是求解接触热阻R2,3的值。

在热流标定试验中，能够准确知道不同热流状态下进入塞块量热计的热流，且能测得塞块后表面相应的温升率，此时将R2,3视作唯一未知量(相当于式(10)中的X)，并赋予一个预估初值；然后以实际测得的热流值作为输入条件，加载到该塞块量热计的仿真模型中，就能得到仿真模型输出的温升率；再将此温升率与标定试验中测得的温升率进行比较，根据比较结果，改变R2,3的值；如此反复迭代，直至仿真温升率与标定试验温升率的偏差小于误差要求(如1%)，此时对应的R2,3就近似为该塞块量热计塞块与隔热套的最佳接触热阻。

采用上述方法求解接触热阻R2,3，有以下说明：

(1) 不同热流条件下算出的接触热阻R2,3可能会略有不同，因为试验测量结果并不仅受R2,3的影响，还受到热电偶焊点工艺、标定系统精度以及数采误差等影响，所以仅能得到一个较为准确的热阻；此热阻除了包含实际的热阻影响，还包含了其他因素的误差影响，可将其视作一个唯一影响该塞块量热计仿真模型的待求变量；

(2) 求解该热阻理论上仅需一个标定状态，但考虑到影响因素较多，应考虑使用2～3个热流状态相互验证。

使用上述方法求解表5中1#塞块量热计的接触热阻R2,3，求解过程如表7所示。热阻初始值设为1×10-3m2·K/W，第二轮迭代结果的温升率偏差已经小于1%；继续以相邻两个高热流状态进行验证优化，最终确定接触热阻约为1.7×10-3m2·K/W。

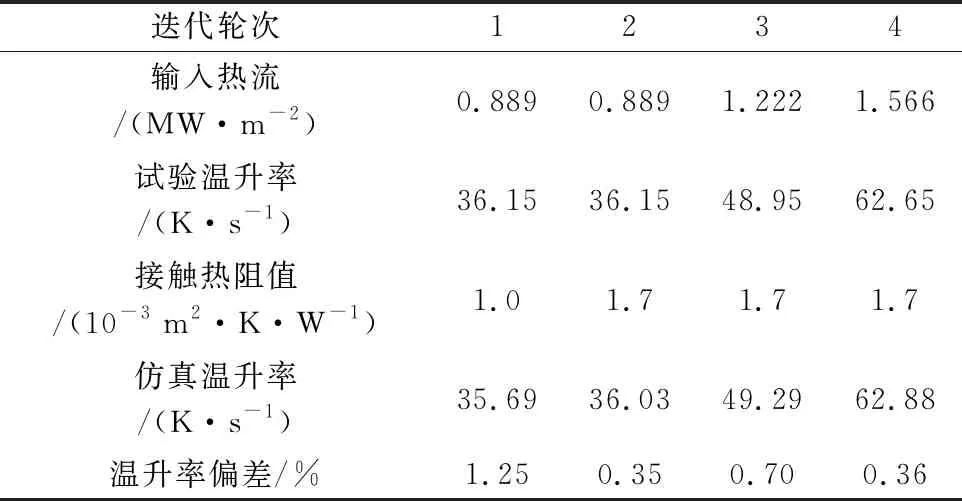
表7 接触热阻的求解过程Table 7 Solution process of contact thermal resistance

受热流标定系统能力限制，未能开展更高热流的验证，仅以表5中的状态4和5这两个相对较高的热流状态验证上述方法的可行性，即假设状态4和5的标准入射热流值未知。对状态4和5的入射热流的求解过程如下(见表8)：

(1) 求仿真模型中的R2,3。表7中已求得其值为1.7×10-3m2·K/W。

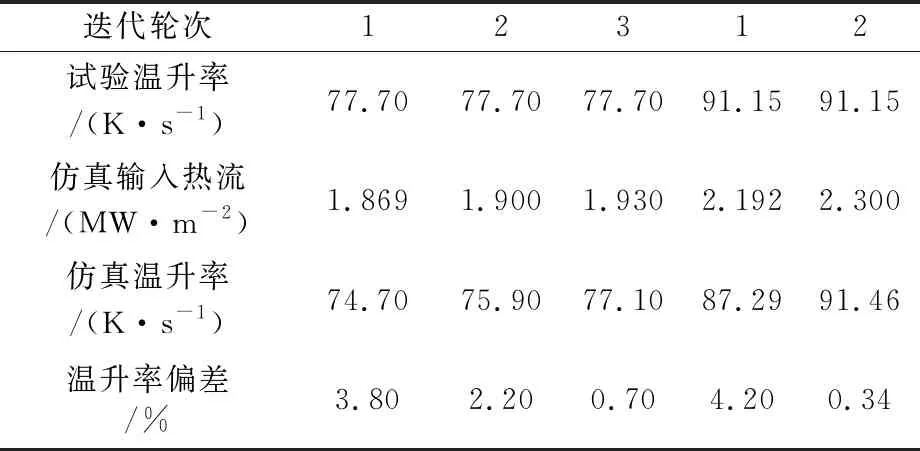
表8 入射热流的求解过程Table 8 Solution process of incident heat flux

(2) 求初始入射热流。试验中已测得状态4和5的温升率分别为77.70和91.15 K/s，根据式(8)可计算得到两状态的热流初始值为1.869和2.192 MW/m2。

(3) 迭代优化入射热流。不断更新仿真模型中入射热流的值，当仿真温升率与已知的试验温升率偏差小于1%时，对应的仿真输入热流值即为较优入射热流。按此迭代方法，得到状态4和5的热流修正值分别为1.930和2.300 MW/ m2，与实际标准热流的误差分别为1.02%和0.30%，小于修正前的4.2%和5.0%，可见该方法能够有效减小计算热流的误差。

4 结 论

本文建立了塞块量热计的仿真模型，并给出了仿真模型的求解方法，仿真和试验结果表明了该方法的可行性，这种求解思路也可应用于类似的传热仿真模型中。提出的直接比对标定方法和基于标定的数值计算修正方法均能降低塞块量热计的热流测量误差。考虑热流标定系统自身误差(3%)后，塞块量热计的热流测量误差小于5%；直接比对标定修正方法的误差相对更小，但要求热流标定系统能覆盖被测热流范围；基于标定的数值计算修正方法对热流标定系统要求较低，适用范围更广。

本文的两种修正方法应用于中空型隔热结构的封装塞块量热计中，可以提高塞块量热计的热流测量精准度，已在电弧风洞试验中得到了验证(与戈登计的风洞试验比对测试结果见文献[11])和推广应用。