鱼游动涡结构PIV实验研究

王福君, 王洪平, 高 琪, 魏润杰, 刘彦鹏

(1.浙江大学航空航天学院 流体工程研究所, 杭州 310027; 2.中国科学院力学研究所 非线性力学国家重点实验室, 北京 100190; 3.北京立方天地科技有限责任公司, 北京 100083; 4.北京航空航天大学航空科学与工程学院 流体力学研究所, 北京 100191)

0 引 言

鱼类经过几亿年进化出高效、高机动的流线型身躯，能够灵活应对复杂的水下环境。其特有的运动方式一直是流体力学的研究热点，对水下航行器的推进有着重要指导意义和应用价值。因此，众多学者通过理论分析、流动显示、粒子图像测速(PIV)实验以及数值模拟等方法对该领域展开了研究[1]。

现有对鱼类的研究根据不同的游动速度将鱼类游动模式大致分为了BCF(Body and/or Caudal Fin)和MPF(Median and/or Paired Fin) 2种[2]。前者依靠身体和尾鳍的摆动来提供动力，使得鱼快速游动；后者依靠胸鳍、背鳍和腹鳍实现原地静止游动。但是对单一的个体而言，鱼的游动会同时表现出2种游动模式，以实现快速、高效的机动。根据Sfakiotakis等[2]的结论，BCF模式和MPF模式分别可细分出多种不同的模式，分别展示在图1(a)和(b)中。BCF模式包含从波动(Undulatory)到摆动(Oscillatory)大致5种游动模式[2]；MPF模式可分为两大类，分别是鳍波动模式、鳍摆动模式[2]。中国船舶研究中心的张军等[3]采用PIV技术对MPF模式下长鳍波动推进的流场流向结构进行实验研究，给出了长鳍在不同截面的相位平均速度场。

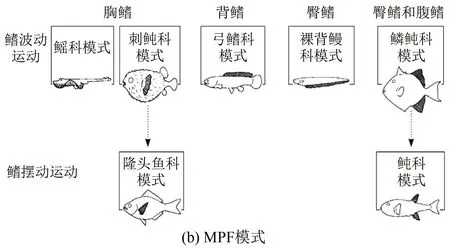
图1 游动模式的演变图[2]

Smits等[1]对鱼的波动和摆动进行了详细的综述。波动运动以长条体型鱼的游动为主，典型代表为鳗鲡；摆动运动又可分为纵摇运动(Pitch motion)和垂荡运动(Heave motion)，以尾鳍发达且成月牙型的鱼类为主，典型代表为金枪鱼。事实上，自然环境中鱼类的游动大多介于波动游动和摆动游动之间，而对于各类游动方式的研究大多仅限于数值模拟，实验上大多也只采用形态学观测或者平面PIV测量，少有定量的三维测量。Borazjani等[4-5]在不同雷诺数Re=ρVd/μ(ρ、V、d、μ分别表示流体密度、游动速度、特征长度、流体黏性)下对鲹科模式 (Carangiform)和鳗鲡科模式(Anguilliform)的游动进行数值模拟，发现鱼游动时尾迹涡环呈现出单行和双行特征。鳗鲡科鱼在游动时由于尾部振幅较小，以致于脱落的涡环形成一条直线，称为单行涡环;而对于鱼尾振幅较大的鱼类游动，尾迹则形成双行脱落的涡环。中国科学技术大学李龙等[6]对鲹科模式的鱼类进行了鱼尾模型实验，发现鱼尾转动和平动的相位差会显著影响鱼尾的推力。蓝鳃太阳鱼的胸鳍运动模式是MPF模式中的刺鲀科模式，Lauder等[7]对蓝鳃太阳鱼的胸鳍进行PIV实验研究，发现鱼胸鳍流场的三维涡结构呈现出单个涡环的特征。

鱼类的游动模式与游动状态密切相关。鱼游动一般可简化为2种游动状态：巡游状态(Cruise)和猝发状态(Burst)[8]。鱼类巡游状态方面的研究有很多，并且也取得了很多重要成果。Mwaffo等[8]通过平面PIV技术对斑马鱼在水中巡游时鱼尾摆动频率、游动速度、头部移动方向进行了相关研究，发现频率、速度、相位角在鱼游动时相互影响。Mchenry等[9]则进行了成年斑马鱼的巡游时间、启动速度、惯性等3个方面的实验研究。模拟仿生方面，活鱼巡游状态一般定义为鱼尾的正弦运动[10]，因此在仿生鱼尾的实验时要控制仿生鱼尾进行正弦摆动，从而可以初步研究机械鱼的水动力学性能[11]。哈尔滨工程大学于凯等[12]进行了双尾的仿生推进器的水动力学实验，结果表明相对于单尾的仿生推进器，双尾布局能够提高推进器的稳定性和灵活性。

相对于巡游状态，鱼猝发(Burst)状态的实验研究则成为国内外研究的焦点。鱼的猝发运动状态也称为逃逸反应(Escape response)、C型启动逃逸(C-start escape response)和C型转弯[13-15]。实验方面，Danos等[15]在不同的流体黏度情况下对鱼类的逃逸反应进行了实验研究，发现高黏度的流体对鱼类逃逸反应的某一个阶段有强烈的阻碍作用。Danos等[16]就斑马鱼转弯时鳍的各种形态变化进行了实验分析，揭示了斑马鱼的双鳍、中鳍和骨架的形态变化情况是转弯游动的重要因素。数值模拟方面，2009年Wang等[17]发现C型启动不仅发生在逃逸反应时还发生在非逃逸反应时。蓝鳃太阳鱼逃逸反应的三维数值模拟结果清晰地显示了尾流的涡结构[14]，该结果可以说明鱼类游动状态的改变是尾流场变化的重要因素。C型游动模式的研究大多还停留在数值模拟和仿生学的研究上，定量的PIV实验研究则很少有人进行。

本文利用平面PIV技术和Tomo-PIV技术分别测量斑马鱼在不同游动状态下的二维尾迹流场和曼龙鱼巡游时的三维尾迹流场结构，并进行了分析。

1 实验设置及测量方案

1.1 平面PIV实验方案

平面PIV实验对象为成年黑色斑马鱼，体长BL=40 mm。实验用水箱大小为400 mm×200 mm×200 mm(长×宽×高)，水箱中用塑料板隔出宽50 mm的流道作为实验测量区域。选用PH=7.2的纯净水，水温在26±0.5 ℃(正常的热带鱼生存温度)。实验前6 h鱼不用进食。

平面PIV实验布置如图2所示。水箱中均匀撒播20 μm的空心玻璃微珠作为示踪粒子。为了照亮示踪粒子，本实验采用200 mJ的双脉冲激光发生器(镭宝Vlite-200)作为光源。其发出的激光波长为532 nm, 脉冲频率为1 kHz，经扩束光路被扩展成为2 mm厚的片光源。扩束光路采用焦距50 mm凸透镜和焦距200 mm凹透镜的组合。图像采集设备为一台配置焦距200 mm尼康镜头的CMOS高速相机，分辨率为1024 pixel×1024 pixel。相机布置在水箱底部向上拍摄鱼游流场。测量区域如图2所示，平行于底壁且位于鱼身中间。实验时，当斑马鱼出现在拍摄区域，并且片光源照射在鱼身中间截面时高速相机开始工作。实验中对每种游动模式连续采集150～250帧粒子图像，以便进行瞬时场分析。图像放大率为0.03 mm/pixel, 对应测量区域大小为30 mm×30 mm。

图2 平面PIV实验示意图

本实验采用北京立方天地科技有限公司的MicroVec软件进行PIV图像分析。查询窗口设置为32 pixel×32 pixel，步长8 pixel×8 pixel。最终速度场包含125×125个矢量。为研究流场结构与游动状态的关系，需从粒子图像中提取斑马鱼的二维形态特征。

根据实验图像的灰度分布，在Matlab软件里采用阈值分割法提取粒子图像中斑马鱼的二维形态。首先对图像进行中值滤波处理，剔除图像上的示踪粒子；然后采用阈值分割的方法提取平面斑马鱼形态特征。效果如图3所示，其中(a)为原始图像,(b)为提取的二维形态图像。

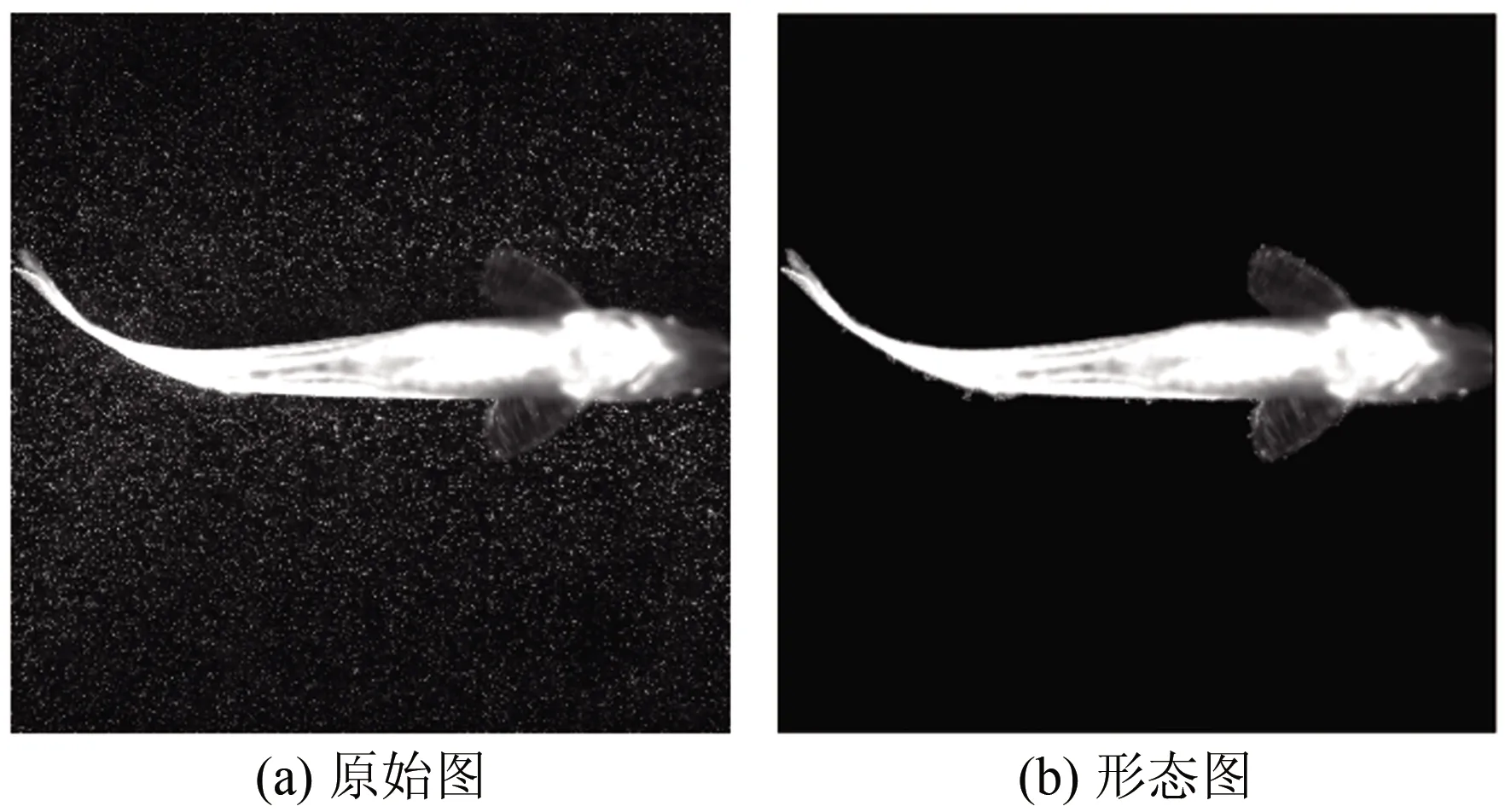
图3 二维形态图

1.2 三维Tomo-PIV实验方案

Tomo-PIV实验对象为成年曼龙鱼，BL=60 mm，选择曼龙鱼作为三维实验对象是因为曼龙鱼体型大，尾迹流场三维结构明显，形态纹理丰富，有利于进行三维形态重构；与之相比，斑马鱼体型较小，纹理较少，三维流动结构不明显。实验在环形水槽中进行，实验段大小为400 mm×200 mm×100 mm(长×高×宽)；在拍摄区域前端悬挂50 g鱼食，选用PH=7.2的纯净水，水温为26±0.5 ℃(正常的热带鱼生存温度)；实验前6 h鱼不用进食。

实验时，环形水槽中均匀散播20～50 μm的空心玻璃珠作为示踪粒子。本实验同样采用了200 mJ的固体激光器。与平面PIV实验所不同的是，脉冲激光通过导光臂和扩束头被扩展成厚度为60 mm的体光源。图像采集设备为4台配置45 mm 尼康移轴镜头的CCD相机，分辨率为2048 pixel×2048 pixel，采集频率为10 Hz。整体实验布置如图4所示，4台CCD相机呈一字型布置在观测区域一侧，调节相机的位置，测量鱼游的尾迹流场。

图4 Tomo-PIV实验示意图

Tomo-PIV的图像分析采用MicroVec标准算法进行。三维重构体大小为60 mm×50 mm×50 mm，包含1090×909×909个体素。计算时采用三维体变形算法，迭代2次。第一次窗口大小为64 pixel×64 pixel×64 pixel，第二次窗口大小为48 pixel×48 pixel×48 pixel，最终步长为24 pixel×24 pixel×24 pixel。得到的速度场经过归一化中值检测、滤波等后处理，并进一步计算出旋涡强度等物理量以便于分析。为了同时提取鱼的形态特征，根据双目立体成像的原理[18]和标定的结果，从其中2个相机的粒子图像中还原出鱼运动的瞬时形态。图5为三维重构实验数据与重构结果图,其中(a)、(b)为2个不同视角的相机图像;在双目立体成像原理和标定拟合的多项式公式下，通过图像上曼龙鱼形态上的独有的特征点信息，重构出曼龙鱼三维形态，结果如图5(c)所示。

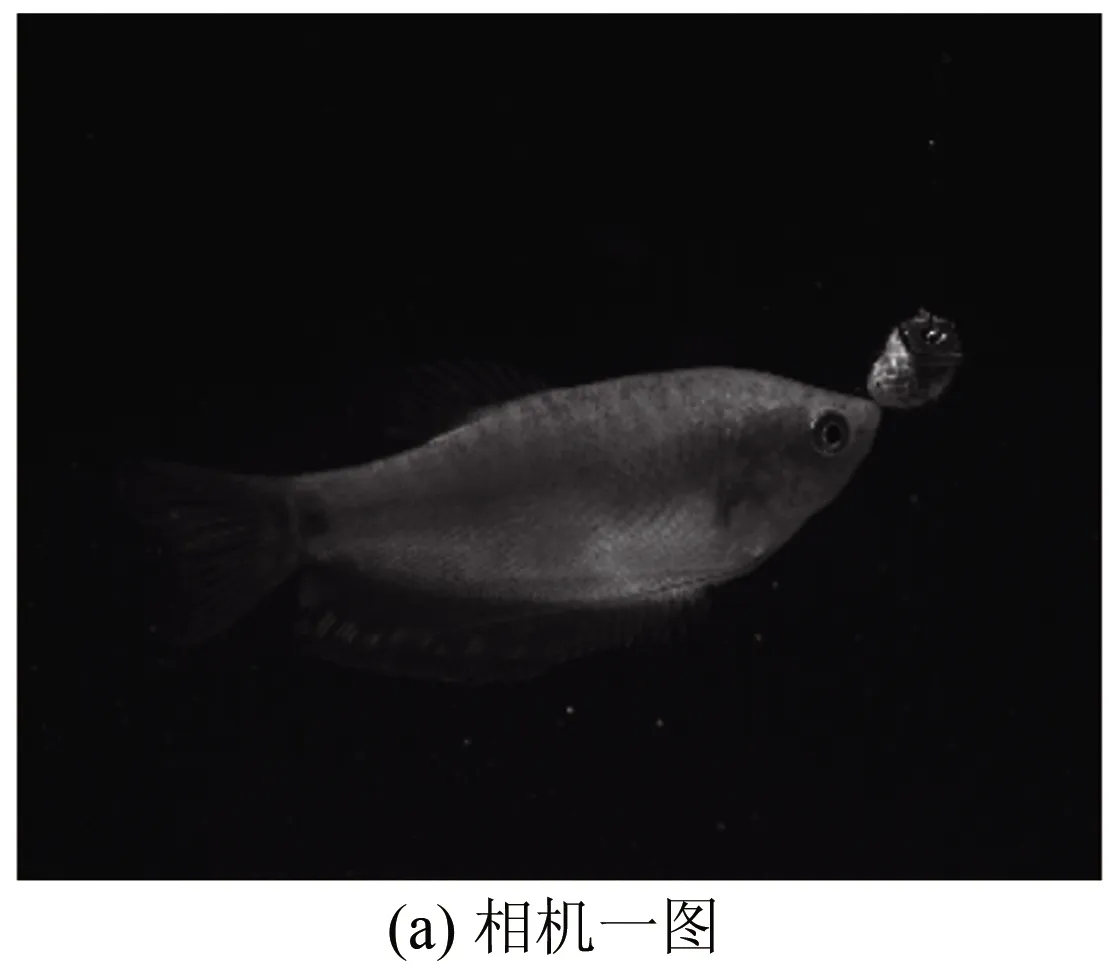
图5 三维重构实验数据与重构结果图

2 实验结果及分析

本节主要分析与斑马鱼不同游动状态相对应的二维尾流场的涡结构，以及曼龙鱼在巡游状态下的三维尾涡结构。斑马鱼游动状态分为启动状态、巡游状态、巡游-C型逃逸过渡状态、C型逃逸状态。根据Williamso等[19]的结论，尾迹涡结构可以分为P模式、S模式、P+S模式。各模式对应的涡脱落模式如图6所示。P模式为尾迹流场在半个周期内有1对运动方向相反的旋涡一同耗散消失；S模式为尾迹流场在半个或者1个周期内仅有1个旋涡出现，并且耗散消失;P+S模式为尾迹流场在1个周期内出现1对运动方向相反的旋涡，并且紧随其后还会出现1个单一的旋涡。除了圆柱涡激振动实验尾迹流场涡脱落模式外，也有学者在圆柱或机翼后安装柔性平板，从而分析不同运动状态下的涡结构[20-21]，以上研究结果将被用于分析斑马鱼的尾迹流场。

2.1 斑马鱼启动状态测量结果

图7为斑马鱼在水中从静止状态到游动状态时刻的连续瞬态涡量场云图，(a)～(h)分别为0、30、60、90、120、150、180和210 ms时刻的涡量云图。从图中可以看出：斑马鱼从静止状态到启动状态，尾部轻微向下摆动，此时尾部后方出现了1个脱体涡1，同一时刻鱼尾前部还存在1个前缘涡2(见图7(c))，前缘涡在鱼尾移动时逐渐增长。这2个涡配对表现出反卡门涡的特征，形成向后射流。当鱼尾向下到达最大位移处后再向上移动时，脱体涡仍存在，前缘涡增长到最强并开始脱落，此时前缘涡2完全脱落，与之前的涡1运动方向相反(见图7(e))，这2个涡结合在一起形成蘑菇状的涡结构。在半个周期内流场中仅有1对涡脱落并且耗散，这就构成了涡脱落的P模式。这2个涡在形成以后逐渐耗散消失，之后鱼尾在摆回至中心位置的半个周期内，仍会出现相同的涡变化特征。

图6 涡脱落模式图

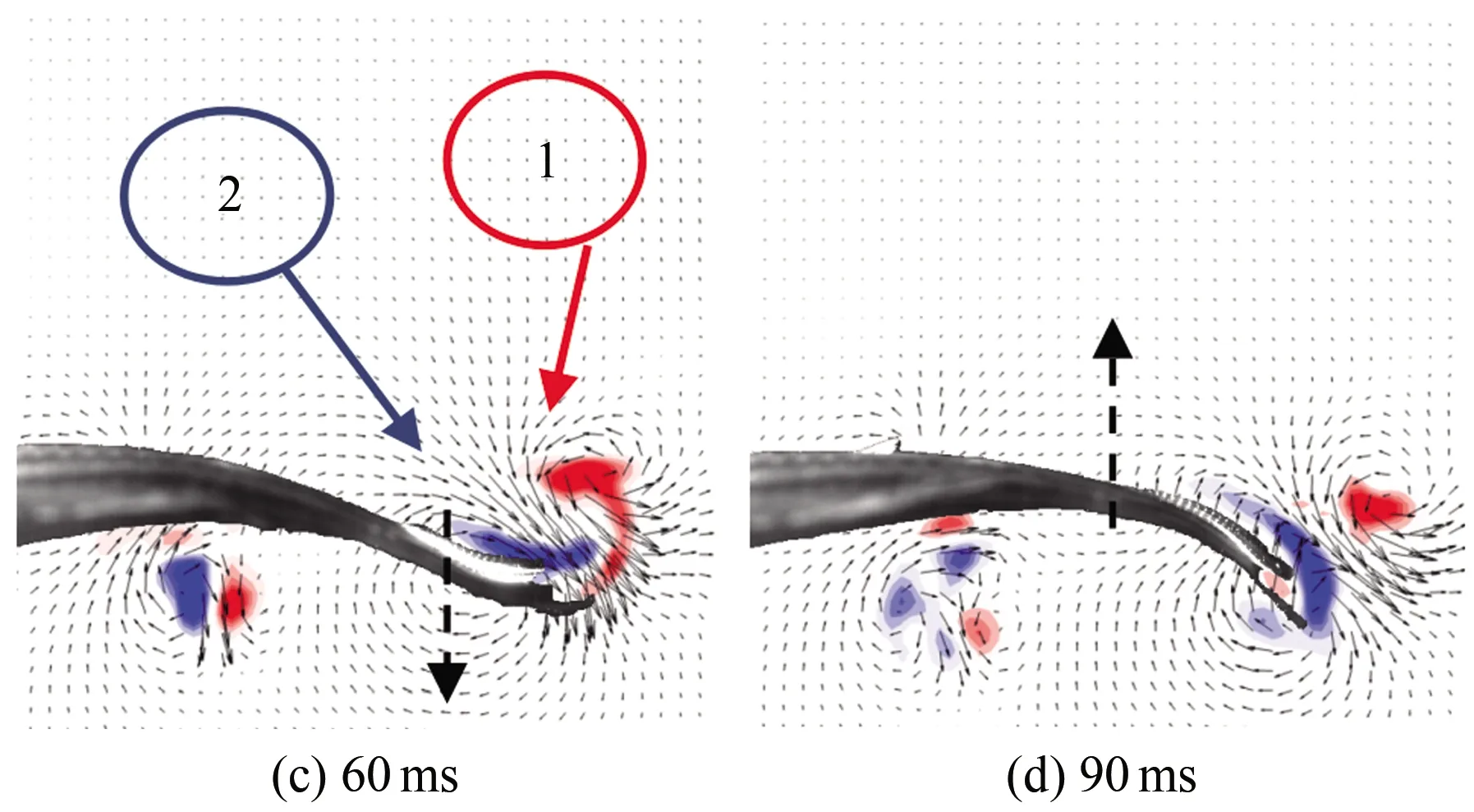
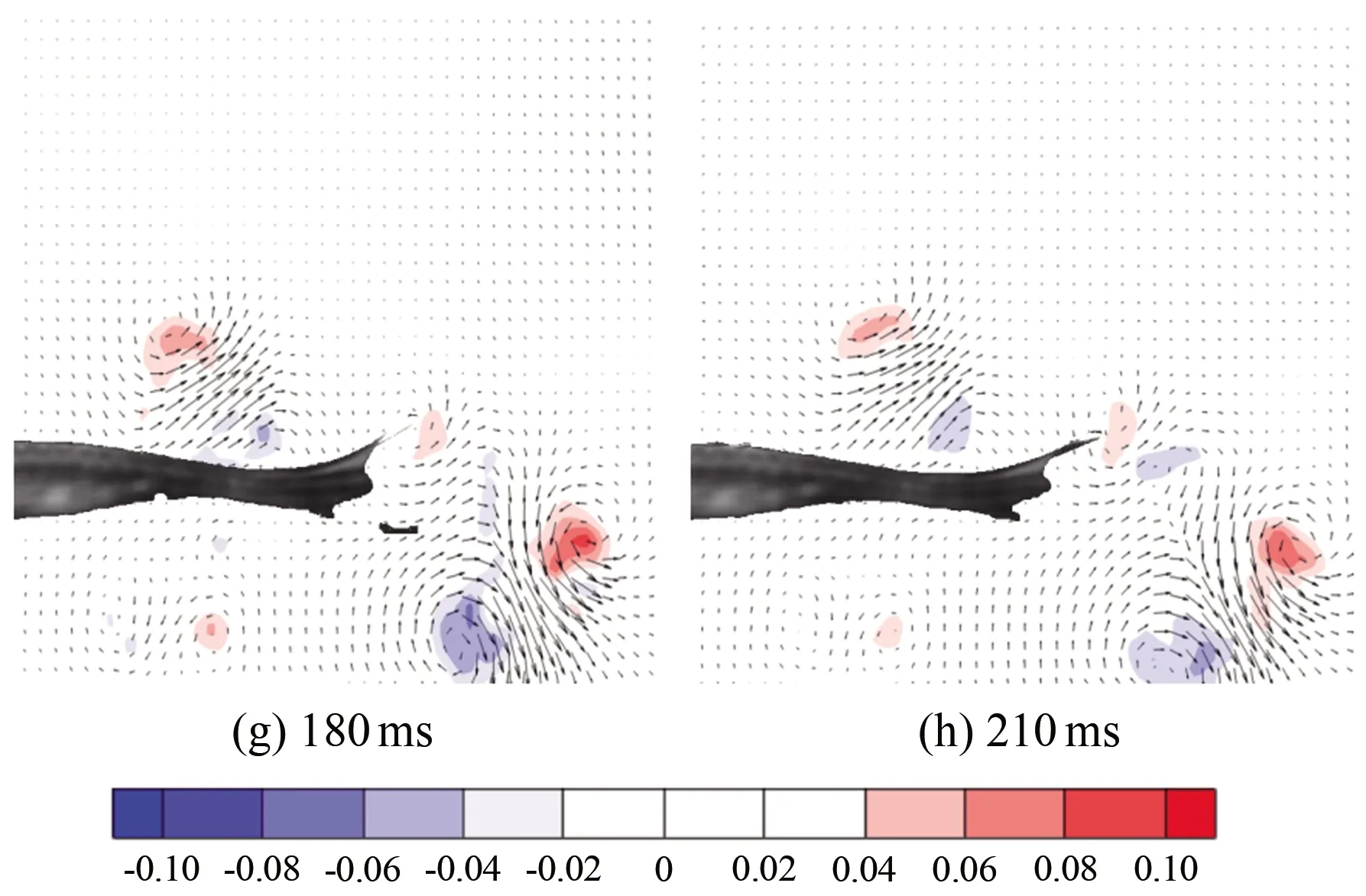
图7 启动状态涡量场云图

鱼瞬态速度的计算以鱼在图像中质心处的速度为基准，如图8所示。在启动状态下,总体而言鱼游动速度表现为上升形式。刚开始启动时的速度为0.305 BL/s，最大速度到达0.375 BL/s。鱼尾的摆动在50和210 ms时为主要的运动状态，此时速度略微下降;正是此时鱼尾的摆动为鱼后面的运动提供了动量，使鱼的速度快速增加。

图8 启动状态速度变化图

2.2 斑马鱼巡游状态测量结果

图9为斑马鱼在水中巡游状态时刻的连续瞬态涡量场云图，(a)～(h)分别为0、10、20、30、40、50、60和70 ms时刻的涡量云图。从图中可以看出，斑马鱼在巡游状态持续游动时，尾巴连续摆动，以鱼水平中线为起点，鱼尾向上摆动时尾后流场会出现1个前缘涡1(见图9(c))，此涡对鱼尾有推动作用，且当鱼尾运动到最大位移处时该涡增强之后开始脱落；当鱼尾开始向下摆动时，周围会出现1个前缘涡2(见图9(f))，而当鱼尾恢复到接近水平位置时，前缘涡2增强后脱落，并与之前脱落的涡1形成P模式的涡脱落结构(见图9(g))。两脱落涡构成反卡门涡，并且都是由前缘涡生长而来,因此在鱼尾运动的半个周期内均会出现相同的涡变化特征。

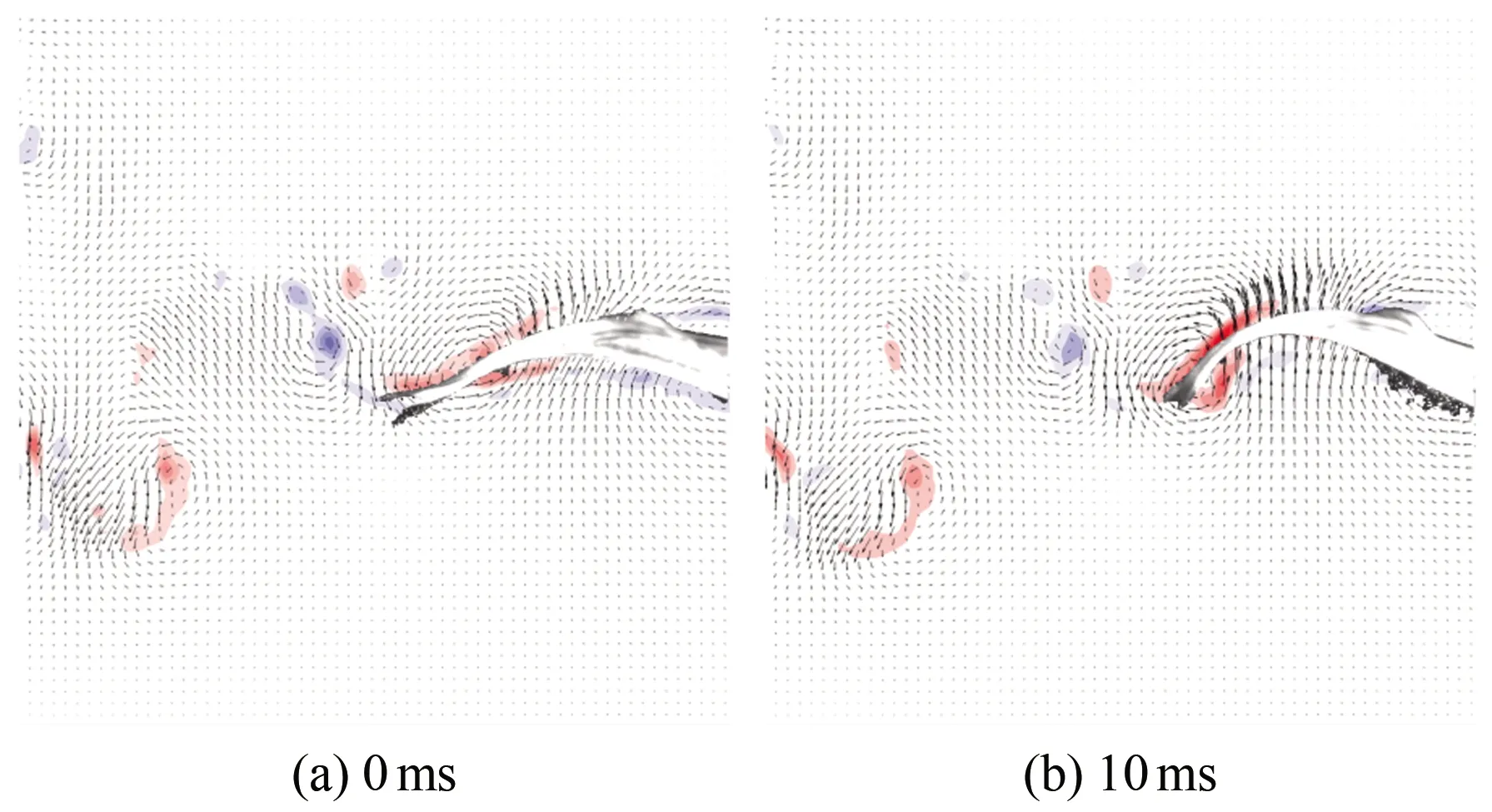
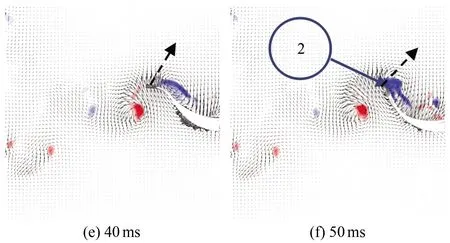
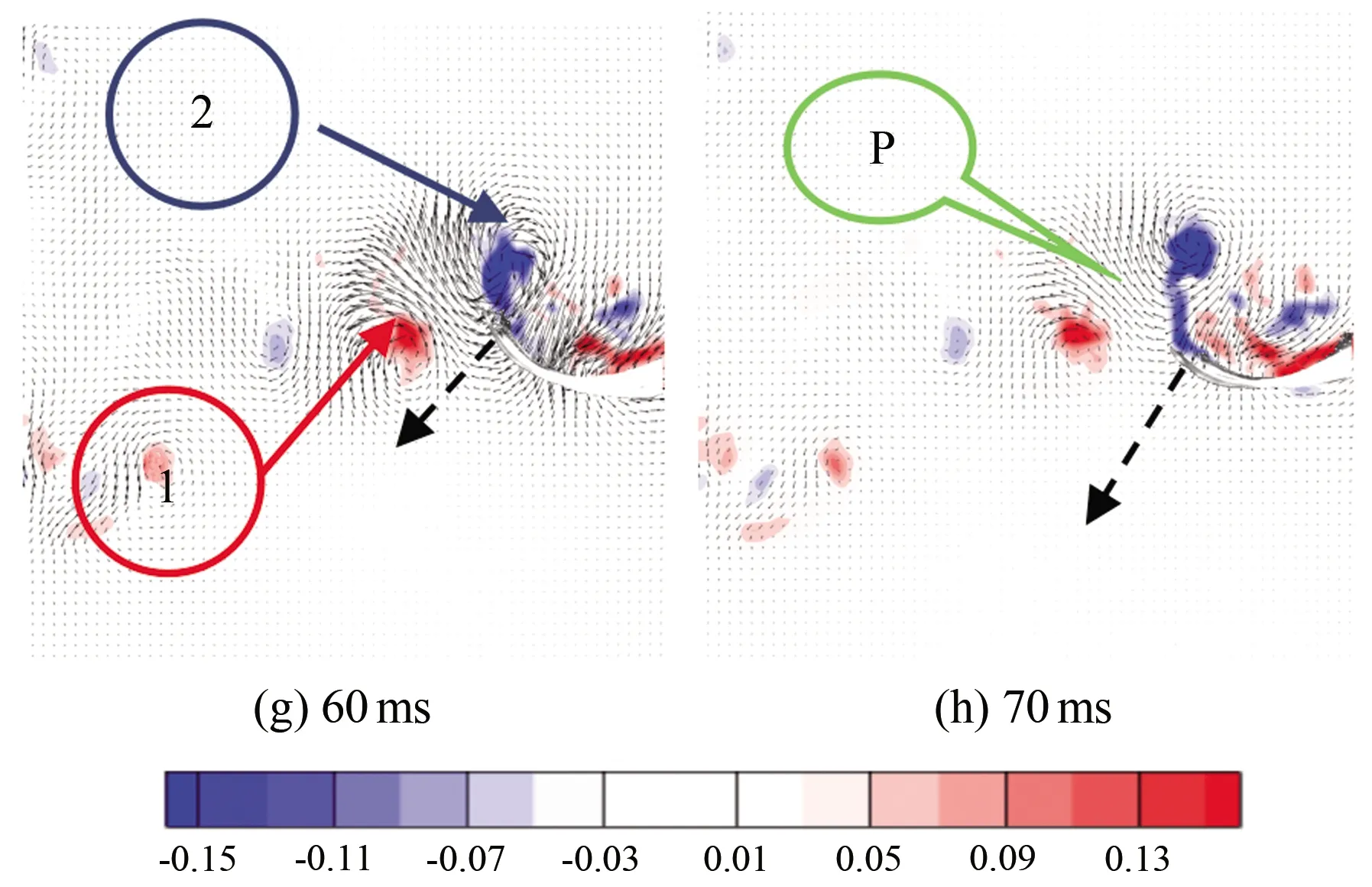
图9 巡游状态涡量场云图

如图10所示，鱼在巡游过程中速度一直维持在0.650～1.125 BL/s。在60 ms处尾迹流场正好脱落成1对P模式的旋涡结构，此时游动速度增加到最大，说明鱼尾前期的摆动为鱼的游动提供了推力。在整个巡游期间，鱼游动的平均速度为0.3625 BL/s(0.0145 m/s)，鱼尾摆动的平均振幅A约为5 mm。由于每个瞬时点间隔10 ms，因此鱼尾摆动平均频率f约为8.57 Hz，可知斯特劳哈尔数为2.96(St=lf/v，l为振幅，f为频率，v为速度，St数为表征流动非定常性的相似准则)。

图10 巡游状态速度变化图

2.3 斑马鱼巡游-C型逃逸过渡状态测量结果

图11为斑马鱼在水中巡游-C型逃逸过渡状态时刻的连续瞬态涡量场的云图，(a)～(h)分别为0、20、40、60、80、100、120和140 ms时刻的涡量云图。斑马鱼从巡游状态转向C型逃逸状态的过程中,游动方向及游动速度未达到逃逸状态时称为过渡状态。从图11可以看出，斑马鱼在巡游-C型逃逸过渡状态时，鱼尾摆动幅度大、方向变化大。以鱼尾开始摆动作为起始点，其向右上方摆动时周围出现了脱体涡1(见图11(b))，在鱼尾逐渐到达最大位移处的过程中脱体涡1脱落，鱼尾进而向左下方摆动，此时出现前缘涡2(见图11(c))，以上两涡构成了反卡门涡。在鱼尾向左下方摆动的过程中前缘涡2脱落，而鱼尾向左下方摆动到接近最大位移处时，又出现另一个前缘涡3(见图11(d))，在鱼继续向右上方游动时前缘涡3脱落。整个周期内鱼尾流场出现3个脱落涡，并且有1对涡同步耗散，另一个涡单独耗散，因此表现出P+S模式的涡脱落结构。流场相对较为混乱，但总体的涡结构还是能看出来的。

鱼的运动角度是以鱼在图像中的质心位置至头部方向的直线为基准，计算其与水平方向形成的夹角大小。从图12可以看出，整个运动过程中鱼的转动角度为121°±1°，平均角速度为12.53 rad/s。在40 ms处鱼的转动角度最大，正好与图12(c)处鱼游动姿态成C形状相对应。

2.4 斑马鱼C型状态测量结果

图13为斑马鱼在水中C型逃逸状态时刻的连续瞬态涡量场云图，(a)～(h)分别为0、40、80、100、120、160、200和240 ms时刻的涡量云图。C型逃逸过程中鱼形态从C型样式变为直线样式。从图13可以看出,在C型逃逸状态时，鱼游动时转动360°。以鱼水平中线为起始点，鱼尾在摆动时首先出现1个脱体涡1，由于此时鱼尾速度为零，所以这个涡称为启动涡[11]。随后由于鱼身体的转动和鱼尾的摆动，鱼尾附近的流场流动附着在鱼尾的边缘，流动方向与鱼尾的运动方向大致相同，以至于引起一连串平面上看起来混乱的涡流动。由于整个周期内尾流场内部仅有1个旋涡脱落并且逐渐耗散消失，所以涡脱落的模式为S。如图14所示，在整个过程中鱼转动角度为193°±1°，平均角速度为21.54 rad/s，在40和90 ms处各有1个峰值，说明在这两处旋转角变化最大，这也是鱼形态呈C型的运动时刻。

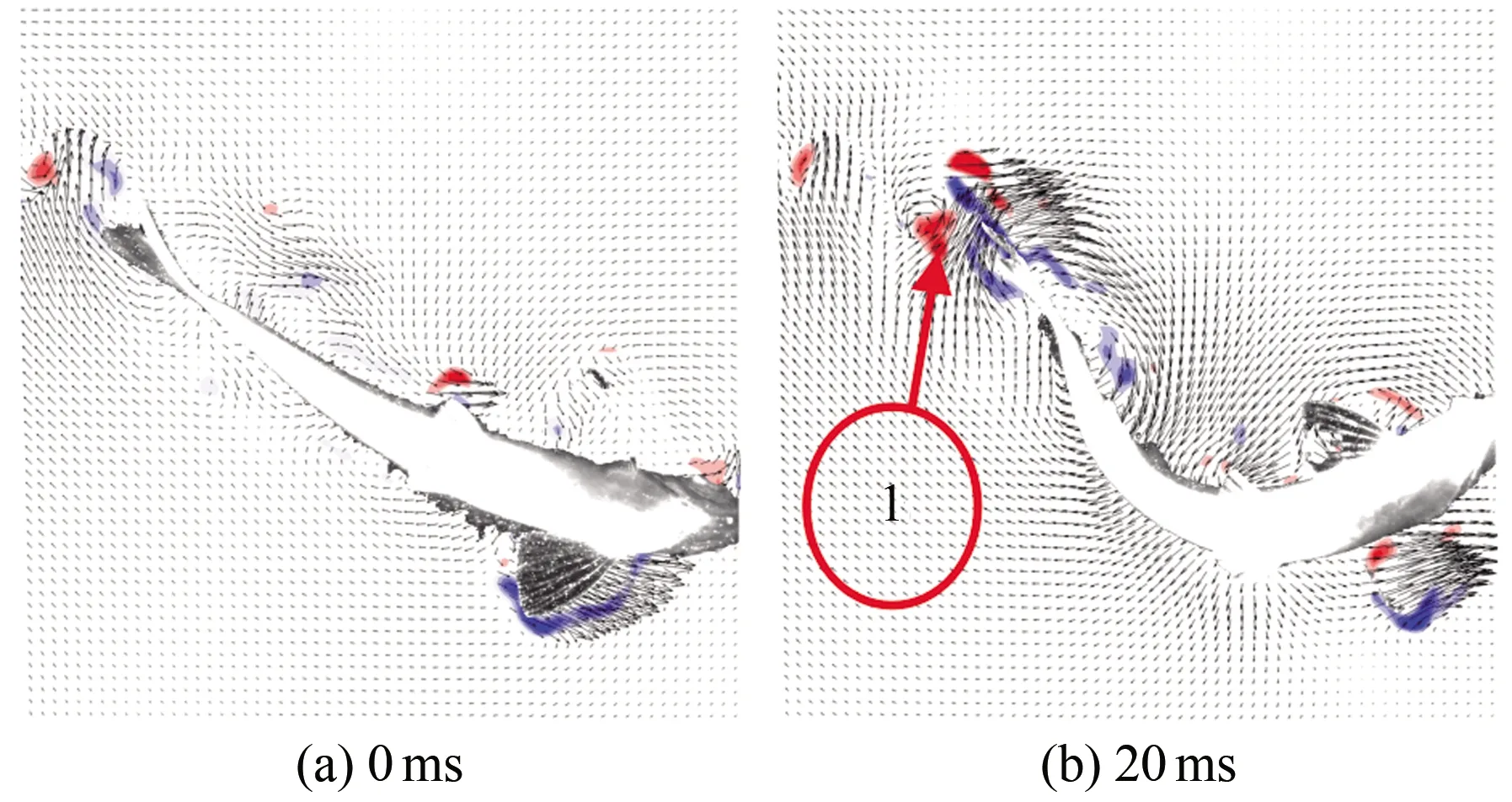
图11 巡游-C型逃逸过渡状态涡量场云图

图12 巡游-C型逃逸过渡状态角度变化图

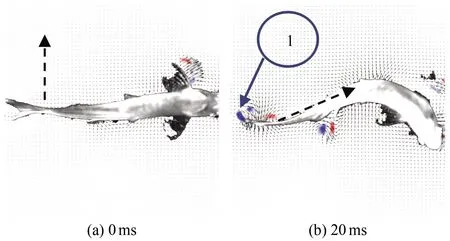
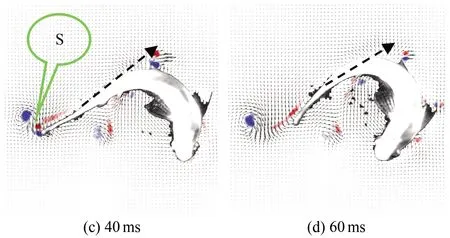
图13 C型逃逸状态涡量场云图

图14 C型逃逸状态角度变化图

2.5 三维测试结果

为便于确定三维尾迹与鱼尾的相对位置，将三维流场和鱼的形态叠加显示，如图15(a)所示。图中可以清晰地看到曼龙鱼巡游时尾流的三维结构，其中出现了经典的连续涡环链[22]。此时流动速度为30 mm/s。图15(a)中的速度场切片云图是根据涡环流向方向所画的，此云图表明通过每个涡环的射流不是水平的。流场内出现了相互连接的3个椭球形涡环，与Flammang等[22]的实验结果一致，所不同的是本实验中鱼尾摆动幅度较小、游动速度较低。

巡游状态下曼龙鱼尾迹流场涡判据准则λci结构如图15(b)所示。在游动期间内二维切面上有4个可见旋涡(V1、V2、V3、V4)、3个射流(J1、J2、J3)。图15(c)为三维结构相互连接的涡环和射流的二维示意图,根据涡环和射流的位置在图中用虚线给出了鱼运动的路径，其中黑色的粗箭头与图15(b)中绿色的粗箭头代表了射流的方向。

为方便描述，将图15(c)内的鱼运动尾迹分为3个不同时刻T1、T2、T3。在T1时刻内鱼尾摆动，产生射流J1和2个旋涡V1、V2，显然涡环1(参考图15(a))是非对称的单独涡环，旋涡V1的强度略大于旋涡V2。射流J1的非均匀分布为鱼质心的移动提供推力。

在T2时刻旋涡V3出现，射流J2是由一对方向相反的旋涡V3、V4形成的。射流J2首先由Sakakibara等[23]发现，并命名为“侧边射流”。鱼尾的摆动方向与射流的流动方向成一定的角度，从而获得了角动量。从图15(b)中可以发现旋涡V3转动的方向与旋涡V2相同，与旋涡V1更接近，表明旋涡V3对射流J1的流动有推动作用。

T3时刻仅能看到射流J3的存在，根据Ting等[24]的研究发现：鱼进入巡游状态时，鱼尾产生射流J3的同时还伴有2个持续的旋涡。所以此时应该还有1个旋涡V5，可能是因为鱼尾对三维粒子重构有影响，未能计算出来。从图15(b)中可以发现鱼尾与涡环3(参考图15(a))等高，表明该涡环是尾鳍的尾缘涡。

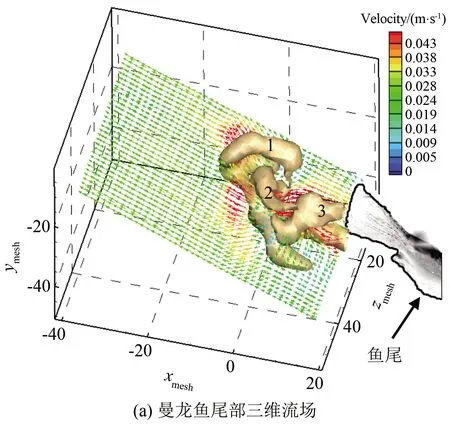
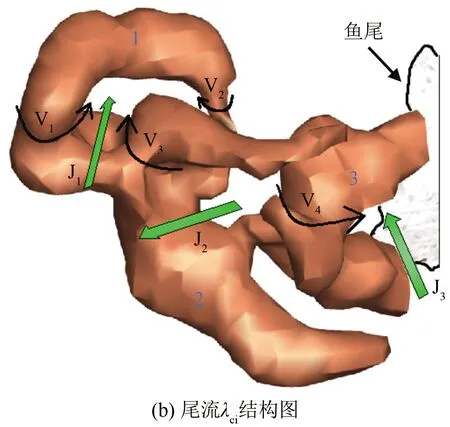
图15 曼龙鱼巡游状态三维尾流场结构

从鱼尾的路径可以发现所有的射流与尾部的方向均存在一定夹角，未出现射流方向与鱼尾平行的情况，表明在巡游状态下射流仅有部分动能为鱼的游动提供动力。与二维结构相比，三维结构更能清晰地说明鱼的尾迹流场特点。

3 结 论

本文以斑马鱼、曼龙鱼为研究对象，针对游动的不同状态，利用平面PIV、Tomo-PIV技术分别测量了不同游动模式下的斑马鱼二维尾迹流场和曼龙鱼巡游时的三维尾迹流场，根据瞬时涡量场的变化情况分析鱼尾涡结构的变化规律。结果表明：

(1) 斑马鱼在启动状态、巡游状态下，半个周期内均出现2个旋涡，分别为起始时鱼尾摆动时产生的涡、鱼尾最大位移后脱落的涡。

(2) 巡游-C型逃逸过渡状态下整个周期内尾鳍流场出现3个旋涡，由于流场扰动导致最后一个涡先耗散。

(3) 斑马鱼在C型逃逸状态下，开始改变游动方向时，仅观察到1个较为明显的涡环，此时鱼尾外围速度为零，产生的涡为启动涡。

(4) 根据涡脱落的不同特征，静水中斑马鱼在启动状态、巡游状态下涡脱落模式均为P，巡游-C型逃逸过渡状态下涡脱落模式为P+S，而在C型逃逸状态下，由于转动方向过程中鱼尾部流场较为混乱，涡脱落模式更为接近S。

(5) 曼龙鱼尾迹流场的三维结构较为清晰地说明，鱼在巡游状态下尾迹流动出现了经典三维连续环涡链结构。

通过斑马鱼、曼龙鱼在水中游动的PIV实验与分析，对不同游动状态下尾迹流场涡结构变化规律有了基本的认识。该研究为鱼类推进的水动力学机理分析打下基础，也为鱼类游动的数值计算提供了验证依据。下一步将进行更为深入的二维旋涡和三维涡环的定量研究。