结合均匀化理论对钢纤维混凝土梁的疲劳性能分析

贺正波，王辉明,2

(1.新疆大学建筑工程学院，乌鲁木齐 830046;2.新疆建筑结构与抗震重点实验室，乌鲁木齐 830046)

0 引 言

为改善混凝土抗拉强度低、易产生裂缝、韧性差等缺陷，常通过在混凝土中添加各种短纤维来改进力学性能。钢纤维因其抗拉强度高、韧性好、与混凝土相容性好等优点，已成为工程实践中应用需求不断增长的混凝土增强材料[1-7]。当前，钢纤维混凝土(steel fiber reinforced concrete， SFRC)已被广泛应用于路面结构、桥梁结构、机场跑道、水工结构及房屋结构等工程中。

近年来，混凝土结构频繁出现的疲劳破坏现象引起了工程技术人员的注意，如:工业厂房中的吊车梁在低负荷往复荷载作用下仍发生断裂[8],水利工程中大坝受波浪反复冲刷作用易造成坝体开裂[9],铁道工程中路枕承受数万次振动荷载反复作用后出现伤损[10],路面工程中机场跑道、高速公路路面因静载应力超过路面强度引起疲劳开裂[11-13]。在疲劳荷载作用下，混凝土固有的易开裂、韧性差、收缩大等缺点也愈加显著，因此疲劳荷载作用成为钢筋混凝土结构设计中必须重点考虑的因素。随着对纤维混凝土新型复合材料研究的逐步深入，研究人员发现钢纤维的加入可有效提高混凝土的抗疲劳性能，国内外相关研究呈增长趋势[14-18]。

黄承逵等[19]通过对二级配的SFRC梁进行疲劳试验，提出了SFRC梁的抗弯疲劳方程；付佩等[20]通过试验与有限元结合的方法研究了钢纤维掺量与再生混凝土疲劳性能的关系，并给出了钢纤维的最优掺量；徐蓉等[21]进行了钢纤维-聚丙烯混杂纤维混凝土柱的低周反复荷载试验，研究发现钢纤维-聚丙烯纤维的混杂使得混凝土内部应力更加分散，阻裂效果较单一纤维更显著；赵燕茹等[22]发现钢纤维可有效减少裂纹产生和提高SFRC梁的极限承载力，承载力随纤维掺量增大而增大；刘月等[23]进行了等幅疲劳圆板试验，研究发现加入钢纤维后混凝土疲劳寿命显著增加，且在低应力水平下钢纤维对混凝土疲劳寿命提高效果更明显。

从现有研究来看，大多数学者仍以试验研究手段为主，结合细观力学理论开展SFRC疲劳力学行为的数值模拟研究较少。因此本文结合细观均匀化理论计算与SFRC弹性模量相关的力学性能参数，建立合理、准确的有限元计算模型，从构件尺寸和纤维长度两个因素出发，进行SFRC梁的抗弯试验模拟，并基于有限元静力计算结果，利用nCode疲劳分析软件研究了SFRC构件的尺寸效应以及纤维长度与疲劳性能之间的内在联系。

1 钢纤维混凝土宏观弹性模量预测及有限元静力分析

均匀化理论认为复合材料的宏观力学性能主要取决于所含夹杂形状的主轴方向和体积分数[24-25]。当复合材料中夹杂主轴方向随机均匀分布时，夹杂形状对宏观力学性能的影响较小，因此本文采用具有模型生成参数较少、生成效率高等优点的球形粗骨料。

预测复合材料宏观力学性能方法中，出现较早的有Voigt并联模型及Reuss串联模型，研究[26]表明这两种模型一般只能预测出宏观力学性能的上限和下限，因此本文采用Mori-Tanaka(M-T)均匀化理论。

1.1 细观均匀化理论和钢纤维混凝土宏观弹性模量预测

(1)M-T均匀化理论

均匀化理论基本原理是用一个等效均质材料的响应替代相应非均质材料的平均响应。通常取一个代表性体积单元(representative volume element， RVE)进行研究，如图1所示。

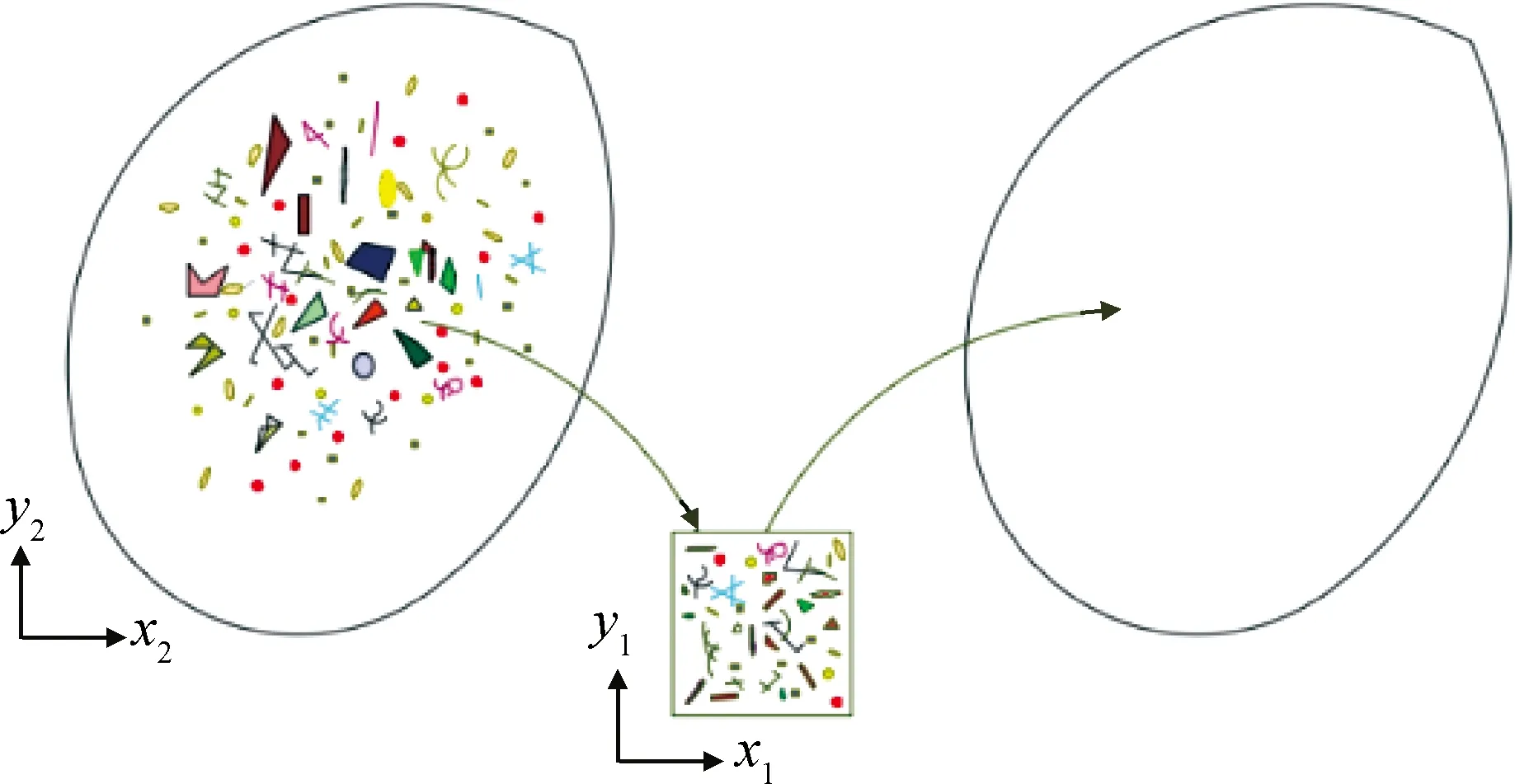
图1 代表性体积单元(RVE)Fig.1 Representative volume element (RVE)

RVE内的微观应力、应变和均匀化后的宏观平均应力、应变的关系如下：

(1)

(2)

(3)

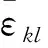
基于Eshebly等效夹杂理论，日本学者Mori和Tanaka[27]建立了广为应用的M-T均匀化理论，给出了非均质材料宏观力学性能的近似计算公式：

(4)

(5)

式中：ζ(I,C0)为Eshebly张量，与材料形状与性质有关。

(2)SFRC弹性模量预测

依据黄承逵等[19]试验中的配合比，其中:纤维为熔抽碳钢纤维，掺量为0%、0.5%、1.0%和1.5%(体积分数,下同)，长度为34.7 mm，等效直径为0.58 mm；骨料粒径选用小石(5～20 mm)、中石(20～40 mm)。相关配合比见表1。

表1 SFRC试验配合比Table 1 Mix proportion of SFRC test

已有研究发现混凝土按照富勒(Fuller)级配公式可以得到较为理想的密实度和强度，因此按照Fuller公式确定粗骨料各粒径对应的体积分数,其表达式为:

(6)

式中:P为骨料通过筛孔直径(d)的累积百分通过率;dmax为最大粒径。

经计算骨料中小石体积分数为13.56%，中石体积分数为16.37%，钢纤维长径比取60。材料属性见表2。

表2 材料属性Table 2 Material properties

根据M-T均匀化理论可求出不同纤维掺量对应的宏观弹性模量，结果见表3。

由表3可知，均匀化理论求得的混凝土宏观弹性模量与试验结果[28]拟合很好，最大误差小于4%。均匀化法属于半解析半数值方法，相比完全数值法节省了大量建模工作，计算量少且准确率高，可以用于补充或替代部分试验，从而快速获得复合材料的宏观力学性能参数。

表3 弹性模量预测值与试验值的对比Table 3 Comparison of predicted and tested elastic modulus

1.2 SFRC梁抗弯试验模拟

(1)SFRC梁有限元数值计算模型

SFRC梁按混凝土试验梁标准尺寸建模，即550 mm×150 mm×150 mm，采用三分点加载方式，约束方式为简支梁约束，为保证计算收敛性采用位移加载。首先考察钢纤维掺量影响，故建4组梁模型(钢纤维掺量0%、0.5%、1.0%、1.5%)。静力计算应用ABAQUS有限元分析软件，其中SFRC梁采用C3D8R三维实体单元，单元大小为10 mm，划分为12 600个单元，有限元模型如图2所示。计算时SFRC弹性模量取前述均匀化理论预测值，泊松比为0.2。

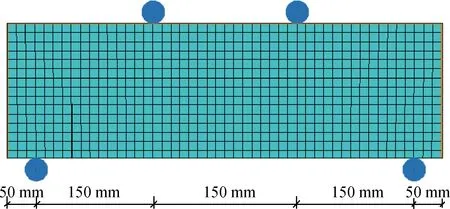
图2 SFRC梁有限元模型Fig.2 Finite element model of SFRC beam

(2)抗弯计算结果及分析对比

在钢纤维混凝土本构关系方面，高丹盈[29-30]通过试验研究了钢纤维长径比、掺量对本构关系的影响，并给出了以长径比与掺量作为参数的SFRC拉、压本构关系，具有较高的可靠性。因此本文采用该SFRC本构模型，得到了应力-应变曲线，各掺量的SFRC拉、压本构关系分别如图3、图4所示。

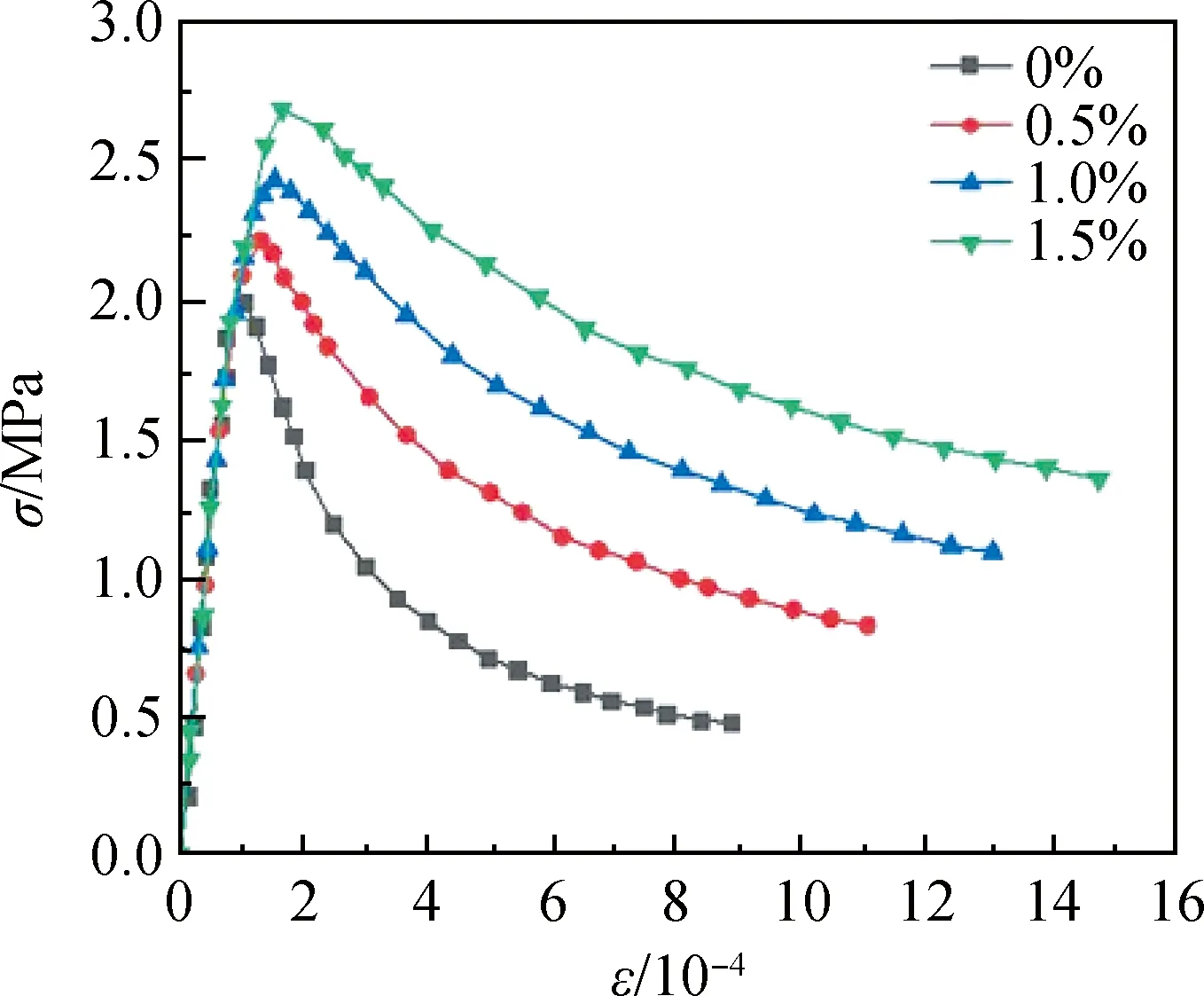
图3 SFRC受拉本构关系Fig.3 Tension constitutive relation of SFRC

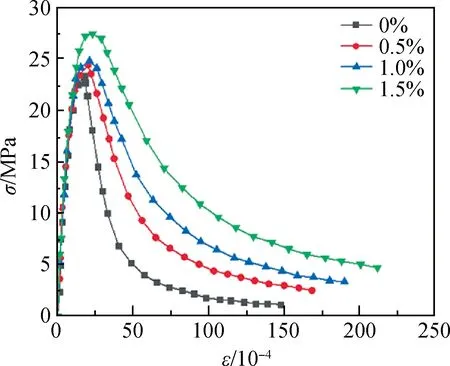
图4 SFRC受压本构关系Fig.4 Compression constitutive relation of SFRC

通过对0%钢纤维掺量的SFRC梁进行抗弯试验模拟，所得荷载-挠度(U-Δ)曲线与试验曲线[31]上升段基本一致，下降段稍有区别，如图5所示。考虑到曲线的形态与SFRC本构关系有较大关系，本文模拟所得荷载-挠度曲线拟合性较好。通过模拟结果与试验结果的对比，验证了模拟有限元模型的可靠性。经计算得到不同钢纤维掺量荷载-挠度曲线如图6所示，可以看出,随着钢纤维掺量增加，峰值荷载提高，即SFRC梁抗弯强度不断提高，其中1.0%掺量和1.5%掺量提高幅度较为明显，且随着掺量增加，下降段不断放缓，说明其韧性也得到了改善。

图5 SFRC梁的荷载-挠度模拟曲线和试验曲线对比(0%掺量)Fig.5 Comparison of load-deflection simulated curve andtested curve of SFRC beams (0% content)

图6 不同钢纤维掺量SFRC梁的荷载-挠度曲线Fig.6 Load-deflection curves of SFRC beams withdifferent content of steel fiber

提取U-Δ曲线中的峰值荷载，经计算可得到SFRC梁四点弯曲抗弯强度，如图7所示。可以看出，在1.5%掺量以下时，SFRC梁抗弯强度随钢纤维掺量增加而近似线性增长，说明钢纤维的掺入可有效改善混凝土的抗弯性能。

图7 不同钢纤维掺量SFRC梁抗弯强度Fig.7 Bending strength of SFRC beamswith different content of steel fiber

2 钢纤维混凝土疲劳试验模拟分析

2.1 疲劳损伤累积准则

疲劳破坏属于脆性破坏，破坏时没有预兆，是一种非常危险的破坏形式。混凝土试件浇筑养护后，试件内部有微小气泡及硬化收缩造成的微裂纹等，因此在使用或加载前已经存在缺陷，在环境及往复荷载作用下会累积损伤，当损伤累积到临界值时便会发生疲劳破坏。

经过数十年的研究，目前较为成熟和常用的损伤模型有Henry损伤模型、Shah损伤模型和Miner损伤准则[32]，其中Miner准则是基于线性损伤累积，因所需参数较少、使用简单而被广泛应用于工程中，并经过了大量试验验证，其不足之处是没有考虑加载频率及荷载次数影响。其他准则需要通过大量试验确定众多参数，且在随机荷载和常幅荷载下其精度并不优于Miner准则。因此分析常幅荷载作用下的疲劳性能采用Miner准则。

Miner准则假定在常幅循环荷载下每次循环造成的损伤变量D为：

(7)

式中：N为当前应力水平下的疲劳寿命；n为常幅循环荷载作用次数。而在变幅荷载作用下n次循环后造成的损伤为：

(8)

式中：Ni为对应应力水平Si的疲劳寿命；ni为对应应力水平Si的荷载作用次数。当总的∑n=N时，损伤变量D=1，结构发生疲劳破坏。

2.2 SFRC梁疲劳试验模拟

(1)SFRC梁疲劳方程选取

黄承逵等[19]通过对二级配SFRC梁疲劳试验数据进行线性回归，建立了各掺量统一的SFRC梁疲劳方程(S-N曲线)，该公式与各纤维掺量的试验结果拟合良好，相关系数R均高于0.949，标准差低于0.020 6，在N为106～107情况下，保证率高达99.87%，故有较高可靠性，本文计算采用该疲劳方程，如式(9)所示：

S=(0.944-0.077 lgN)[1+(0.063+0.050 8 lgN)(lf/dfρf)0.188 2+0.021 7 lg N]

(9)

式中：S为不同应力比；N为不同应力比下的疲劳寿命；lf/df为钢纤维长径比；ρf为钢纤维掺量。

(2)疲劳计算结果与试验对比

基于前述有限元静力计算结果，使用nCode软件进行疲劳分析，荷载映射方式为常幅循环荷载，求解器选用SN分析引擎。经疲劳计算得到4根梁不同应力比下的疲劳寿命及疲劳强度，所得疲劳寿命结果与黄承逵等[19]试验结果进行对比验证，可以看出，模拟计算结果除0%掺量与试验有些许差异外，其余三种掺量情况拟合良好，试验-模拟的S-N曲线对比如图8所示。

图8 不同钢纤维掺量下S-N曲线对比图Fig.8 Comparison of S-N curves with different content of steel fiber

不同钢纤维掺量下SFRC梁的应力-寿命曲线如图9所示，可以看出，相同应力下钢纤维掺量越多，SFRC梁寿命越长，且应力比越低，寿命增幅越大，疲劳寿命大约可提高101.2～102.04次。图10为不同钢纤维掺量下SFRC梁疲劳强度。从图10可以看出，随着纤维掺量的增加，疲劳强度不断提高，相较于素混凝土疲劳强度可提高约0.18～1.55 MPa，由此表明可通过添加钢纤维增加混凝土梁的使用寿命和提高其疲劳强度。

图9 不同钢纤维掺量下SFRC梁的应力-寿命曲线Fig.9 Stress-life curves of SFRC beams withdifferent content of steel fiber

图10 不同钢纤维掺量下SFRC梁疲劳强度Fig.10 Fatigue strength of SFRC beams withdifferent content of steel fiber

3 尺寸效应及纤维长度对疲劳性能的影响

根据已有研究，影响结构力学性能的因素同样影响其疲劳性能，但影响程度不尽相同。目前可以概括为三个方面：第一是工作条件(荷载特征、环境温度等)；第二是尺寸效应、缺口效应等；第三是材料本身(混凝土级配、纤维分布形式等)[33]。

影响SFRC疲劳性能因素众多，除上节讨论的钢纤维掺量因素外，本节将从疲劳寿命分析中常见的另外两种因素进行疲劳分析，即尺寸效应及钢纤维长度为控制变量，钢纤维掺量定为1.0%。

3.1 尺寸效应

在以往疲劳强度试验中早已发现同种材料不同尺寸构件的疲劳寿命相差很大，往往构件尺寸越大，疲劳强度越低，寿命也越低，故提出疲劳尺寸系数ξ，即大尺寸试件与小尺寸试件疲劳强度的比值：

(10)

式中：SL为大试件疲劳强度；SS为小试件疲劳强度。疲劳强度为结构在无限寿命(N>200万次)下对应的强度。通常标准试件对应的尺寸系数为1，构件尺寸越大，疲劳尺寸系数则越小，大尺寸结构设计中应考虑尺寸系数的折减。

对钢纤维掺量均为1.0%的3个SFRC梁(L550：150 mm×150 mm×550 mm；L1000：300 mm×300 mm×1 000 mm；L1450：450 mm×450 mm×1 450 mm)进行疲劳性能分析并得到疲劳尺寸系数、疲劳强度及S-N曲线，从而得出试件尺寸对疲劳强度和寿命的影响。图11、图12分别给出了不同尺寸梁的应力-挠度曲线和S-N曲线，图13为不同尺寸梁的疲劳强度和疲劳尺寸系数曲线。

图11 SFRC梁应力-挠度曲线(1.0%掺量)Fig.11 Stress-deflection curves of SFRC beams (1.0% content)

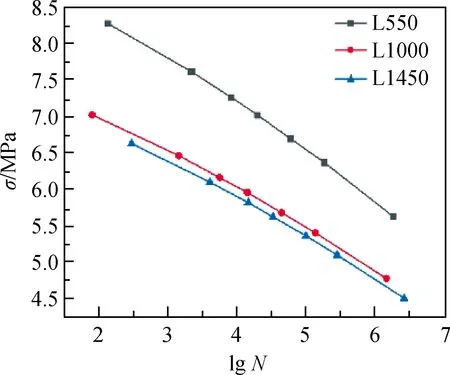
图12 SFRC梁应力-寿命曲线(1.0%掺量)Fig.12 Stress-life curves of SFRC beams (1.0% content)

静力分析结果表明，随尺寸增大，抗弯强度降低，强度降幅呈先增大后减小的趋势，L1000和L1450相较于L550静力强度降幅分别为1.29 MPa、1.80 MPa，表明尺寸效应对抗弯强度影响较大，但随尺寸继续增大，尺寸效应影响减弱。

通过疲劳性能分析可以看出，同样荷载作用下，疲劳寿命、强度都随试件尺寸增大而减小，降幅呈先增大后减小趋势，L1000和L1450寿命减少104.42～105.63次，疲劳强度分别降低0.91 MPa、1.01 MPa，尺寸系数也呈现相同规律，说明随尺寸增大，疲劳性能也趋于稳定。综上所述，无论是静力分析还是疲劳分析，尺寸效应都明显存在，但会随尺寸增大而减弱，因此大体积混凝土结构设计中应当充分考虑尺寸效应影响。

3.2 钢纤维长度

针对1.0%掺量下3种钢纤维长度(25 mm、35 mm和45 mm)的SFRC梁(L25、L35、L45)建立不同纤维长度SFRC梁的S-N方程，从而进一步探究纤维长度对SFRC梁疲劳性能的影响。静力分析如图14所示，可以看出纤维长度对静力性能影响较弱，应力-应变曲线几乎一致。应力-寿命与疲劳强度曲线分别如图15、图16所示。疲劳分析中，纤维长度对疲劳性能影响较为显著。由图15和图16可知：钢纤维越长对SFRC梁抗疲劳性能越有利；疲劳寿命方面，纤维越长寿命越长；相较于素混凝土，L25、L35、L45疲劳强度分别提高0.60 MPa、0.90 MPa和1.03 MPa。

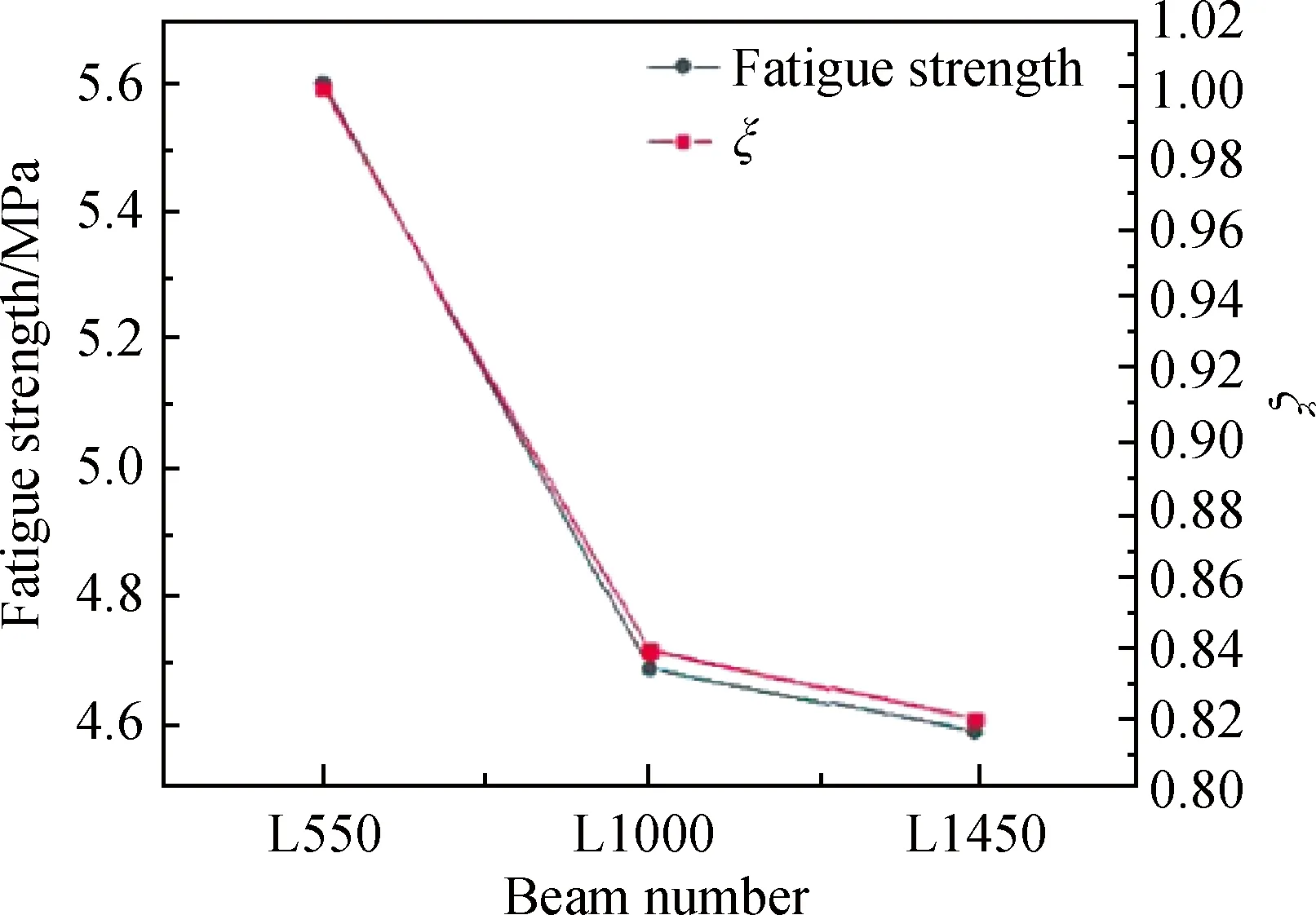
图13 SFRC梁疲劳强度和尺寸系数曲线(1.0%掺量)Fig.13 Fatigue strength and size factor curves ofSFRC beams (1.0% content)

图14 SFRC梁应力-挠度曲线Fig.14 Stress-deflection curves of SFRC beams

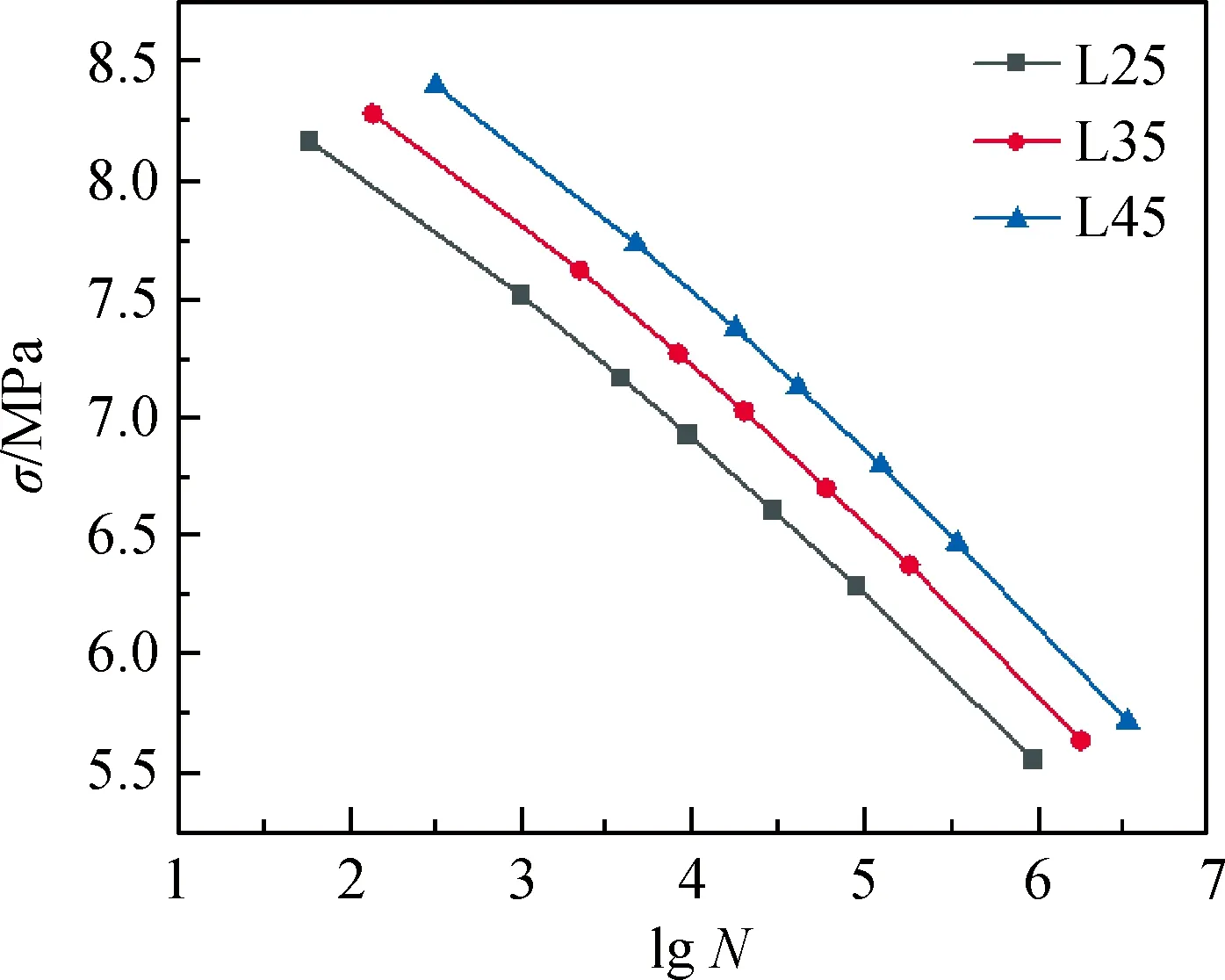
图15 SFRC梁应力-寿命曲线Fig.15 Stress-life curves of SFRC beams

图16 不同钢纤维长度的SFRC梁的疲劳强度Fig.16 Fatigue strength of SFRC beams withdifferent fiber length

4 结 论

(1)钢纤维可以大幅提高混凝土梁疲劳寿命，应力水平越低、纤维掺量越大，增幅越大。在相同应力大小下，寿命大约可提高101.2～102.04次；在0.5%～1.5%纤维掺量下，疲劳强度可提高约0.18～1.55 MPa。

(2)SFRC梁尺寸效应对疲劳强度和疲劳寿命都有一定影响，但随着尺寸增加，尺寸效应对疲劳性能影响减小，在大体积钢纤维混凝土疲劳设计中应当充分考虑尺寸效应影响。

(3)钢纤维长度对SFRC梁静力性能影响较弱，但对疲劳性能影响较为显著；纤维长度越长，抗疲劳性能越好，相较于素混凝土，25 mm、35 mm和45 mm钢纤维分别可提高混凝土疲劳强度约0.60 MPa、0.90 MPa和1.03 MPa；纤维长度增加，SFRC梁疲劳寿命也相应增加。