求解双层伪单调变分不等式的惯性次梯度超梯度算法

方长杰， 张瑞瑞

（重庆邮电大学 理学院，重庆400065）

1 序言

设C为Hilbert空间H中的非空闭凸集，A、F是H→H的2个连续映射，〈·，·〉和‖·‖分别是H中的内积和范数.本文将考虑如下双层变分不等式问题（BVIP）：寻找点x*≥VI（C，A），使得

其中，VI（C，A）表示如下变分不等式问题（VIP）的解集，寻找y*≥C使得

众所周知，VIP问题（2）等价于不动点问题：找到一个点x*≥C，使得

其中λ取任意正实数.求解VIP（2）最简洁的方法是投影方法，该方法在可行集上只进行一步投影.但是，这种方法的收敛性需要一个较强的假设，即映射算子A为强单调且Lipschiz连续的.为了避免这种强烈的假设，Korpelevich［1］引入求解鞍点问题的超梯度方法，并将其推广到有限维和无限维Hilbert空间中的VIP问题，其迭代步骤为

双层变分不等式问题（1）是拟变分不等式问题以及具有均衡约束的均衡问题的特例［5-7］；同时，它们涵盖了一些具有均衡约束的数学规划问题［8］、双层最小化问题［9］、变分不等式问题［3，10］和二层凸规划模型［11］等.基于这些原因，有必要研究双层变分不等式问题.最近，Thong等［12］提出了求解双层伪单调变分不等式问题的超梯度方法.在该方法中，映射A是伪单调的、Lipschitz连续的，但Lipshiz常数需要事先知道.

惯性型方法起源于含摩擦重球系统（HBF）的隐式离散化方法，其主要特点是每个新的迭代点依赖于前2次迭代［13］.随后，将该惯性技术推广到求解极大单调算子的包含问题［14］.近年来，惯性类型算法的研究越来越受到人们的关注，如惯性向前-向后分裂算法［15］、惯性道格拉斯分裂算法［16］和变分不等式的惯性型方法［17］等.

受上述研究工作的启发，本文通过结合惯性项和次梯度超梯度方法，提出求解双层变分不等式问题的惯性次梯度超梯度算法，并获得强收敛性结果.和文献［12］相比，本文通过类Armijo线性搜索准则的应用，映射A假定是伪单调和Lipschiz连续的，但不需要事先知道Lipschiz常数.同时，通过数值实验将算法3.1和文献［3，12］中相应的算法进行比较，验证本文算法的有效性.

2 预备知识

设H是一个实Hilbert空间，而C是H中的一个非空闭凸子集.用xn⇀x表示序列｛xn｝弱收敛到x，用xn→x表示序列｛xn｝强收敛到x.对于每个x，y≥H，以及α∈R，有

对∀x≥H，在C中存在1个唯一的点z=PC x，使得‖x-z‖≤‖x-y‖，∀y≥C.PC称为H到C的投影.

则称T是β强单调的.

（v）称算子T是序列弱-弱连续的，如果对任意的序列xn弱收敛到x，则序列Axn弱收敛到Ax.

众所周知，如果F：H→H是在H上β-强单调和L-lipschitz连续的，且VI（C，A）是Hilbert空间H的非空、闭凸子集，那么BVIP（1）有一个唯一的解［20］.

引理2.4［21，引理2.1］假设C是一个实Hilbert空间H上的非空有界闭凸子集，且A：C→H是伪单调连续映射，则x*是VI（C，A）的一个解当且仅当

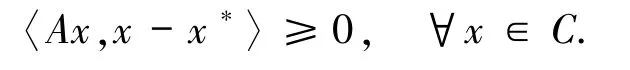
引理2.5［12］设α∈（0，1］，ρ＞0且F：H→H是L-Lipschitz连续和β-强单调映射.定义映射Tρ：H→H如下：

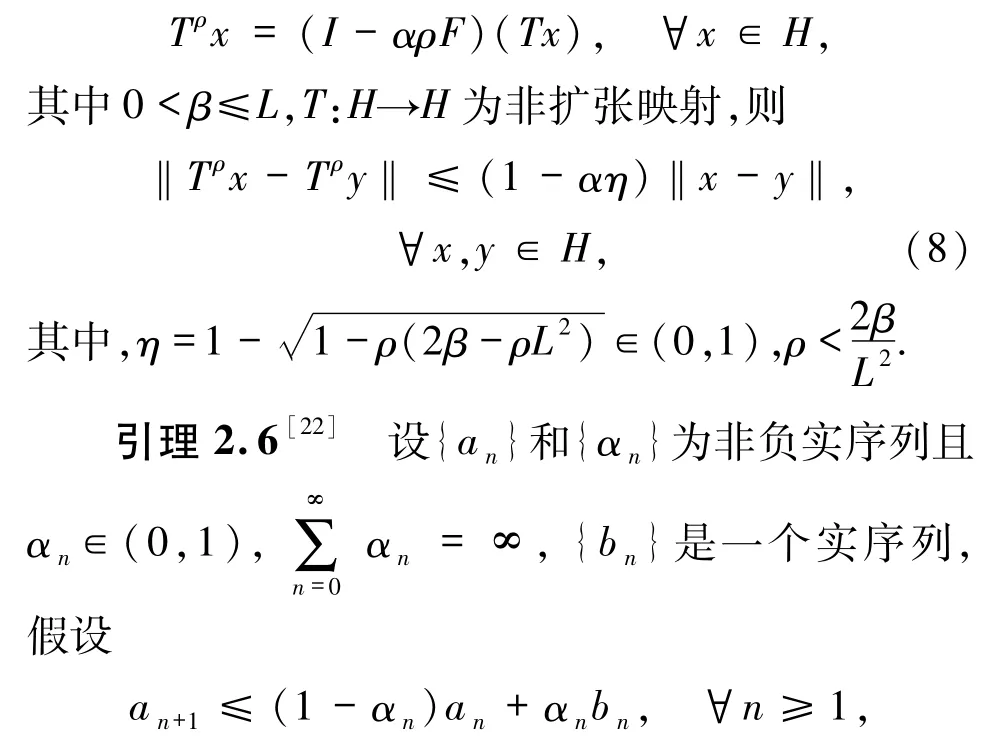
3 主要结果

做如下假设：

（A1）可行集C是实Hilbert空间H的非空、闭凸子集；

（A2）映射A：H→H是Lipschitz连续和伪单调的，在C上是序列弱连续的；

（A3）VIP（2）的 解 集 是 非 空 的，即VI（C，A）≠∅；

（A4）映射F：H→H是H上β-强单调和L2-Lipschitz连续的，且L2≥β.此外，定义p是BVIP（1）唯一的解；

证明分4个步骤来证明.

第一步 证明xn、wn和zn是有界的.由引理3.3，有

4 数值实验

提供一些数值实验来验证算法的有效性.处理器为Intel（R）Core（TM）i3-4010U CPU@1.70 GHZ的系统环境下，使用版本为8.4.0.150421（R2014b）SP1的MATLAB进行数值实验.在表1和表2中，“Iter”表示迭代次数，“CPU”表示以s为单位的CPU时间.ε表示当‖xn-x*‖≤ε时，迭代停止.此外，图形注释中的“ISEA”“SEA”和“MSEA”分别表示本文的算法3.1、文献［12］中的算法3.1和文献［3］中的算法3.1.在图1中，纵坐标表示｛‖xn-x*‖｝（n=1，2，…）的值，横坐标表示运行时间t.

N是n×n阶矩阵，B是n×n阶斜对称矩阵，且矩阵N和B中的元素是在（-2，2）中随机选取的.矩阵D是n×n阶对角矩阵，且对角线元素取值范围为［0，2］（矩阵M是正定矩阵）.方便起见，选取向量d为零向量.

接下来给出第二个映射算子A的2种选择.

例4.1定义

和C：=｛x∈R2：0≤xn≤1，n=1，2｝.A是在C上伪单调和L2-Lipschitz连续的，其中L2=1/2.在我们的算法中，参数取值为μ=0.73，τ=0.22，γ=0.75，ρ=3.63，α=0.042；在文献［12］的算法3.1中，参数取值为μ=0.94，α=0.53，γ=0.91；在文献［3］的算法3.1中，参数取值为μ=0.66，τ=0.03，γ=1.54（图1和表1）.

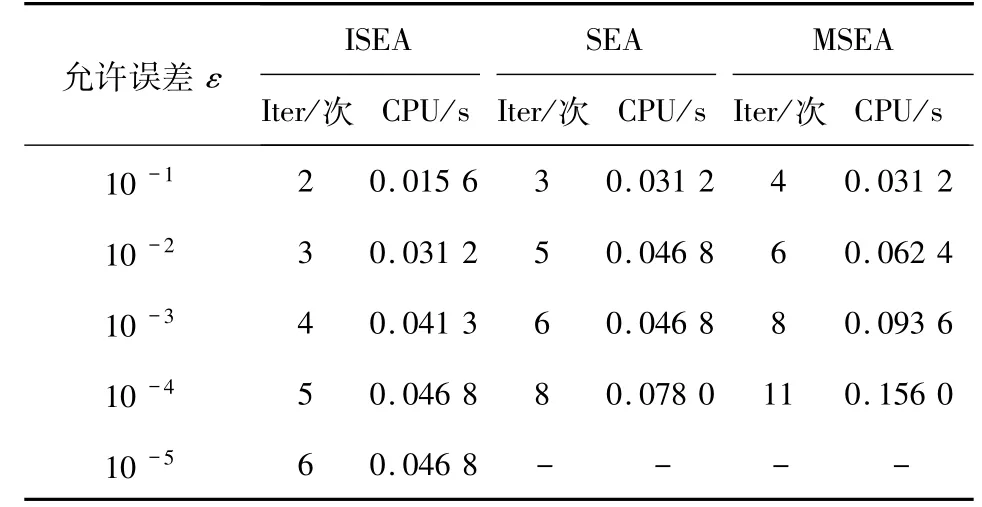
表1 例1中CPU和迭代次数比较Tab.1 Comparison between CPU and the iteration number in example 1

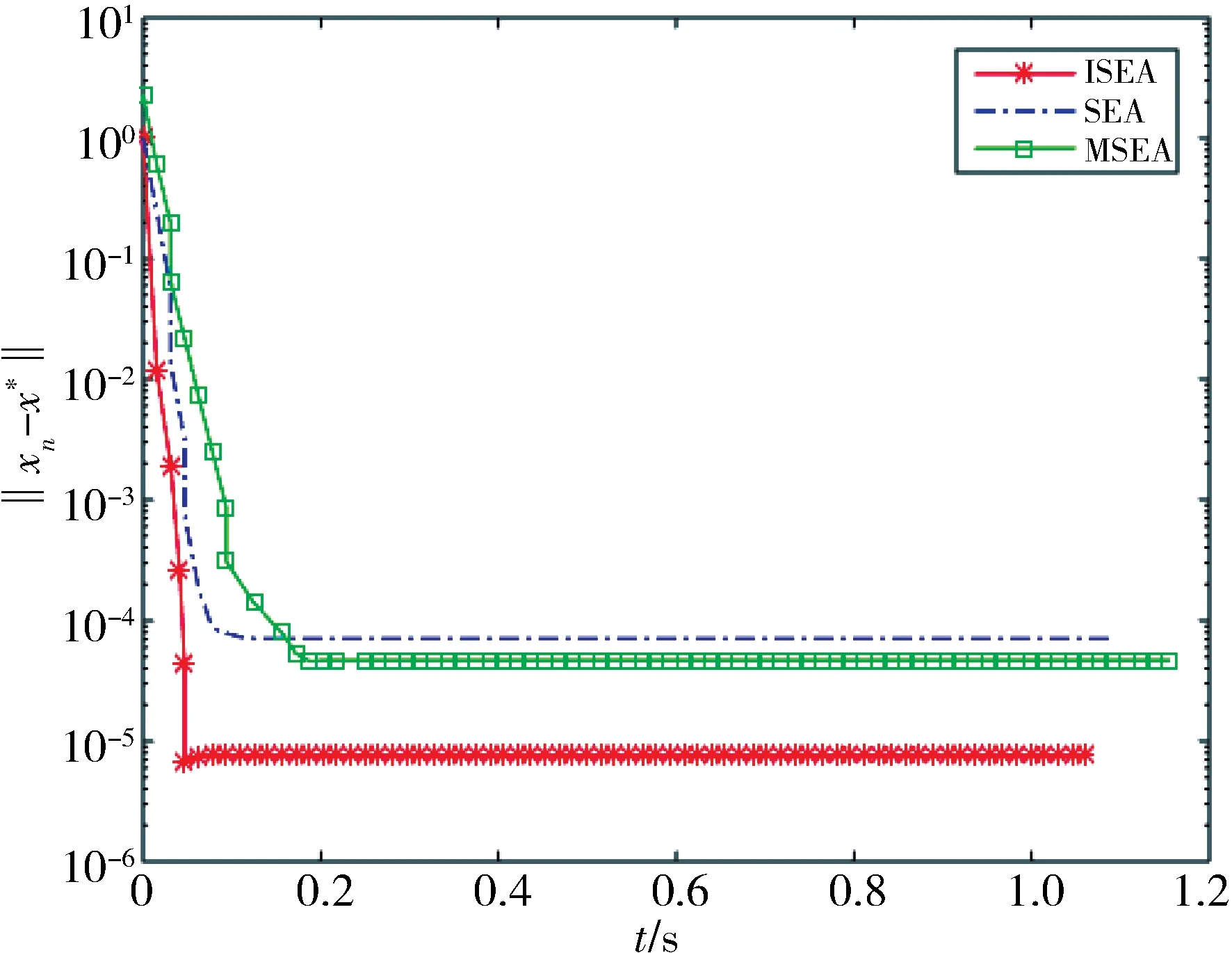
图1 例4.1中的‖xn-x*‖和时间的关系Fig.1 The relationship of‖xn-x*‖and time in Example 4.1

例4.2设H=R2且

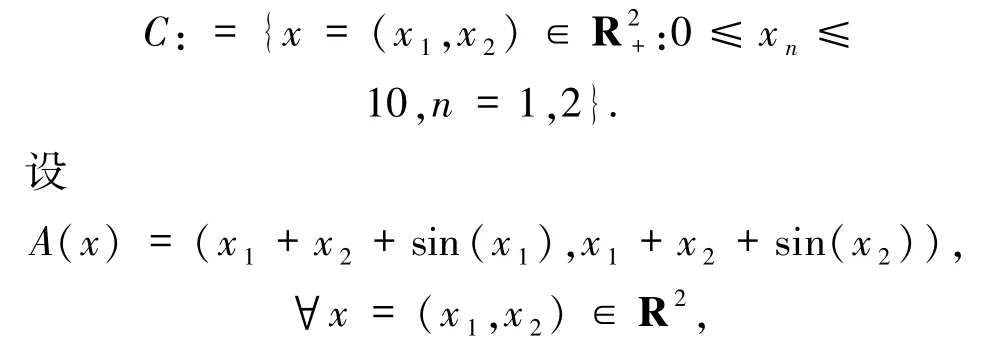
其中，A是单调的，L2-Lipschitz连续，参数L2=1/2.算法参数取值为μ=0.92，τ=0.39，γ=0.28，ρ=0.44，α=0.8；在文献［12］的算法3.1，参数取值为μ=0.36，α=0.75，γ=0.49；在文献［3］的算法3.1中，参数取值为μ=0.76，τ=0.34，γ=0.45，见图2和表2.

表2 例2中CPU和迭代次数比较Tab.2 Comparison between CPU and the iteration number in example 2

图2 例4.2中的‖xn-x*‖和时间的关系Fig.2 The relationship of‖xn-x*‖and time in Example 4.2