奇异积分算子在加权调幅空间上的有界性

刘慧慧，唐 剑

（阜阳师范大学 数学与统计学院，安徽 阜阳236037）

0 引言

基于时-频分析的基本工具——短时Fouier变换，Feichtinger在文献［1-2］中率先给出调幅空间Mp,q(p,q∈[1,∞])的概念，该空间也被称为Feichtinger函数空间.之后，Kobayashi［3］将Feichtinger的经典定义推广到一般的0＜p,q≤∞情形.近年来，调幅空间已成为调和分析及方程理论研究中的重要函数空间，不仅被广泛应用于研究奇异积分算子、Fourier乘子、Hörmander乘子、么模Fourier乘子及拟微分算子的有界性等调和问题，还被应用于讨论非线性Schrödinger方程、非线性热方程等偏微分方程解的适定性等问题.关于该空间更多的应用，读者可见文献［4-14］.

沿曲线的奇异积分算子的有界性问题，多年来吸引众多学者的关注.Zielinski在其博士论文［15］中讨论如下定义的沿曲线的强奇异积分算子在Lp上的有界性问题，并得到当曲线γ(t)=t2时，算子Ta,b

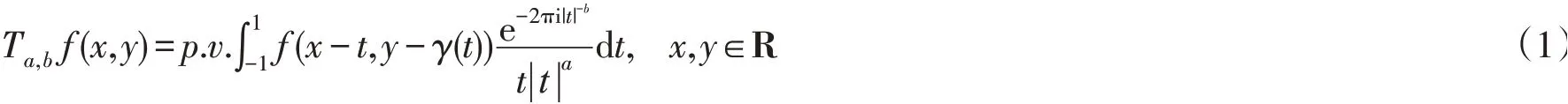
在L2(R2)上有界的充要条件是b≥3a.文献［16］改进上述结果，证明对更一般的曲线γ(t)=|t|k或sgn(t)|t|k(k≥2)，当b＞3a＞0时，算子Ta,b在Lp(R2)上有界，其中指标p满足此外，还证明算子Ta,b在L2(R2)上有界的等价条件为b≥3a.

受文献［16］的启发，文献［17］讨论算子Ta,b在加权调幅空间上的有界性.证明当b≥3a且或时，算子Ta,b在空间上有界，其中1≤p≤∞,0＜q≤∞且s∈R.利用函数分解及振荡积分估计，本文首先对0＜p＜1的情形进行补充，得到对于0＜p＜1,0＜q≤∞且s∈R，算子Ta,b在空间上有界，详见下文定理1.

综合文献［17］的结果及定理1可见，调幅空间中指标p的取值范围明显大于其在Lp中的取值范围，表明在讨论沿曲线的奇异积分算子的有界性问题上，调幅空间比Lebesgue空间更合适.此外，调幅函数空间也更适合在其上研究沿曲面的奇异积分算子的有界性问题.如Cheng等在文献［18］中对如下定义的沿齐次超曲面的强奇异积分算子

文中使用C表示任一正常数，其在不同位置取值可能不同，但均与主要变量无关.

1 预备知识及关键引理

记S(Rn)为Schwartz函数空间且S′(Rn)为其对偶空间.对于定义在S(Rn)上的函数f，其Fourier变换定义为f∧(ω)=∫f(t)e-2πiω·tdt，Fourier反演变换定义为f∨(t)=f∧(-t).函数f的平移算子及调幅算子分别定义为Tx f(t)=f(t-x)和Mω f(t)=e2πiω·t f(t)，其中x,ω∈Rn.

设函数g∈S(Rn)非零且1≤p,q≤∞,s∈R，加权调幅函数空间为关于范数

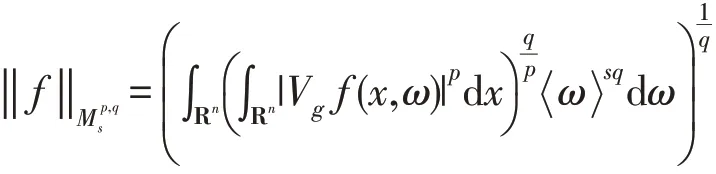
定义1［3］给定非零函数g∈Φα(Rn)及0＜p,q≤∞,s∈R.调幅空间定义为全体关于范数

有限的Schwartz函数f构成的集合.对于p或q=∞，需将Lp或Lq范数替换为本性上确界L∞.

引理1［19］设0＜p,q≤∞且g∈Φα(Rn)，则

（1）不同的测试函数g1,g2∈Φα(Rn)定义的空间Mp,q s(Rn)具有等价拟范数；

（2）若0＜p0≤p1≤∞且0＜q0≤q1≤∞,s∈R，则嵌入到

（3）当0＜p,q＜∞时，Schwartz函数空间S(Rn)在调幅空间中稠密.

为证本文主要结果，需要以下定义的Wiener共合空间W(ℱLp,L∞)(Rn).

定义2设g∈Φα(Rn)且0＜p＜∞.Wiener共合空间W(ℱLp,L∞)(Rn)定义为所有关于范数

有限的缓增广义函数f∈S′(Rn)组成的函数集合.

引理2［10］设0＜p＜∞且定义函数空间则

引理3［20］当0＜p＜1,0＜q≤∞且s∈R时，如果σ∈W(ℱLp,L∞)，则定义为

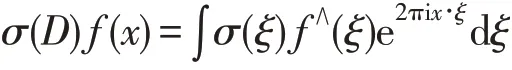
的乘子算子σ(D)在加权调幅函数空间上有界.

引理4［21］设定义在区间(a,b)上的实值函数φ(t),φ(t)是光滑的且k∈N.若对任意的t∈(a,b)，φ(t)满足且

（i）k≥2，或者

（ii）k=1且φ′(t)为区间(a,b)上的单调函数时，则有数Ck独立于φ和λ的选取.

2主要结果及其证明

定理1当k∈N且b＞3a时，若这里的常上有界，其中0＜p＜1,0＜q≤∞且s∈R.

证明通过对算子做Fourier变换，得，则由式（1）定义的算子Ta,b在加权调幅空间

因此，可将算子Ta,b写成其中Fourier乘子可整理为

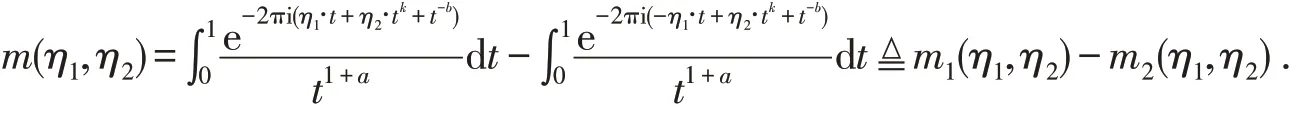
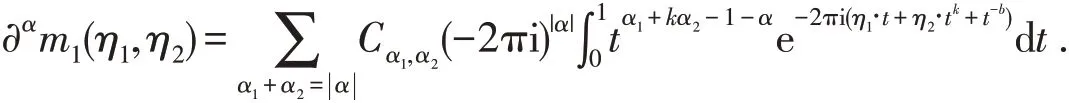
当k≤2时，对任意的其，函数φ(t)的三阶导数满足理4可得由引从而对任意的

对于k＞2的情形，下面分k≥b+4和k＜b+4两种情形来讨论.选取正常数μ1,μ2,δ使得μ1,μ2＞δ.若k≥b+4，记k-2=(b+1)(1+μ1)；若k＜b+4，则记b+2=(k-2)(1+μ1).再令c1,c2为2个正常数且满足下面分别考虑3种情形.

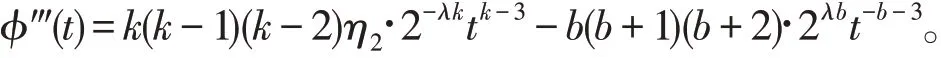
基于关于正常数的假定，此情形的估计将被分成如下2种子情形来考虑.

综合3种情形，当b＞3a时，均有成立，证毕.

定理2设函数h(y)为Rn-1上的实值有界、径向函数，且在[0,∞)上几乎处处可微.定义在Rn-1上的函数Ω是零次齐次的且Ω∈L1(Sn-1).若幅空间且b＞3a时，由式（2）定义的算子T*在加权调上有界，其中0＜p＜1,0＜q≤∞且s∈R.

证明根据Fourier变换，可将算子T*f写成其中η∈Rn-1,ηn∈R且乘子为

由 引 理3，只 需 证m*(η,ηn)∈W(ℱLp,L∞).若 记γ′=(γ,γn)∈Nn-1×N，则 只 需 证 对 所 有 的，函数∂γ′m*(η,ηn)的L∞范数是有限的.利用极坐标变换可得

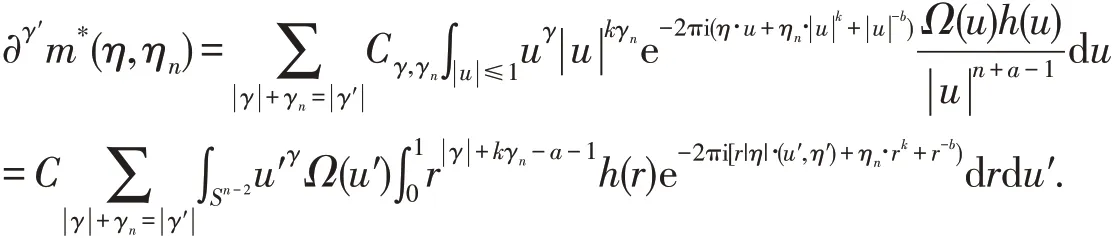
当k≤2时，对任意的，有由Van der Corput引理计算可得从而对b＞3a，有

若k＞2，其证明可类似定理1的证明进行处理，对任意的仍成立

3小结

基于奇异积分算子Ta,b的Lp有界性及其在一般调幅函数空间上的映射性质，本文通过函数分解结合振荡估计得到该算子在加权调幅空间上的有界性，对已有结果进行一定的补充,并类似得到高维情况下一类沿齐次曲面的奇异积分算子T*在加权调幅空间的有界性.综合已有结果可见，调幅函数空间在一定程度上可以作为经典Lebesgue函数空间的良好替代.