线性过程方差变点估计的相合性及收敛速度

董三英，魏岳嵩，张婷婷

（淮北师范大学 数学科学学院，安徽 淮北235000）

0 引言

在统计学中，变点问题自20世纪70年代以来一直是一个热点课题.变点是指在一个序列或过程中，在某个未知时刻序列或过程的某个统计特性发生变化.变点问题的统计推断就是依据具体的背景，对这个未知的时刻做出估计，并对估计量的性质进行统计分析.

由于方差在统计应用中被解释为一种风险，它被广泛应用于经济及金融等领域.序列方差中发生变化点的时刻在文献中得到相当多的关注.例如，Inclan等［1］利用累积平方和的方法检测不相关序列中方差的多重变化.Gombay等［2］利用累积和（CUSUM）统计量检测和估计独立序列中的方差变化.Wichen等［3］开发自回归模型方差变点的迭代似然估计.文献［4］研究线性过程中方差变点的比率检验.Berkes等［5］提出一种CUSUM检测来检测线性过程的协方差结构的变化.Shi［6］分析基于观测和的CUSUM估计量的强收敛性.秦瑞兵等［8］针对线性过程给出强相合估计，并给出收敛速度是关于n的函数.秦瑞兵［9］针对线性过程方差变点比率检验存在势过低的情况提出新的检验统计量.赵文芝［10］构造CUSUM型统计量研究相依序列均值方差同时存在变点的估计问题.

本文研究线性过程模型方差变点的相合性，并且给出它的强弱收敛速度.相较于文献［8］，本文对线性过程模型的统计量做出一些改变，文献［8］只给出强相合性，并没有给出收敛速度，本文增加基于该CUSUM型统计量对模型做出一些分析，得到更一般形式的相合性及其收敛速度.

1 模型及假设

假设Y1,Y2,…,Yn为一列线性过程的随机变量序列，且满足

其中：μ,σ1,σ2都是参数，且σ1≠σ2.τ0=k0/n是一个变点，ei是一个MA(∞)过程，其表达形式为

为研究CUSUM估计量的强弱收敛性质，首先给出以下假设

（A）ζk,k=1,2,…的均值为0，方差为1；成立.

（C）对于任意的k，有

2 主要结论

当已知μ时，不失一般性，假设μ=0，对于模型（1），在通过检验或事先知道线性过程随机变量序列存在变点的条件下，用基于CUSUM统计量的方法估计变点τ0和k0，其CUSUM估计为

其中

γ为满足条件0≤γ＜1的参数.

引理1［11］令Y1,Y2,…,Yn为随机变量序列，A1,A2,…,An为σ代数.假设Yj是适应于Aj的(j=1,2,…,n)，且对于1≤j≤n，其中Y0=0，同时对于每一个j有0≤aj≤1，令常数c1≥c2≥…≥cn≥cn+1=0，r≥1，1≤m≤n.那么对于任意的x＞0，有

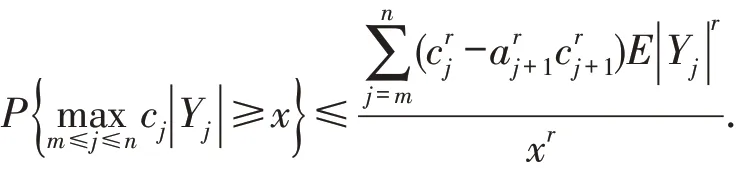
引理2［11］设X1,X2,X3,…为鞅差序列且r≥1，那么存在正常数ar≤br使得

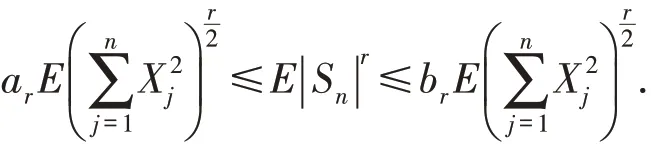
定理1若Y1,Y2,…,Yn是满足模型（1）的随机变量序列，它的变点估计τ^n=k^/n，如果假设（A）（B）（C）成立，则τ^是τ0的相合估计.

证明为方便起见，记

当k≤k0时，

当k≥k0时，同理有

故

当k=k0时，

由三角不等式得

综合式（5）和（6）有

如果τ≤τ0，由中值定理有

如果τ＞τ0，有1-τ＜1-τ0，由中值定理

记

结合式（8）（9）和（10），可得

结合式（7）和（11）有

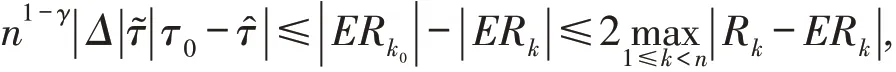
即

则∀ε＞0，欲证τ^的相合性，只需证明n→∞时，

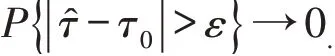
由式（12）得

注意到

由引理1引理2和cr不等式，对于任意正整数r＞2和任取η＞0，有

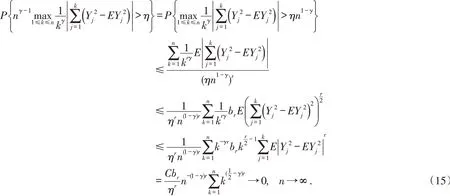
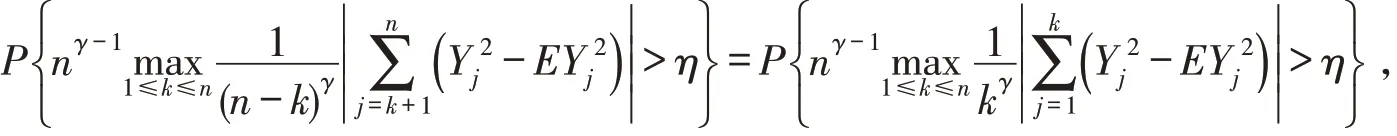
类似有

综合式（14）（15）和（16）有

再由式（12）和（17）有

综上，定理1得证.

定理2在定理1的条件下，弱收敛速度为，其中，

l(n)为满足的慢变函数，δ为满足的常数.

证明令g1(n)为单调递增且满足的函数.对∀ε＞0，欲证τ^的收敛速度，只需证明

类似于定理1的证明知

定理3在定理1的条件下，强收敛速度为

其中

证明欲证τ^的强收敛速度，由Borel-Cantelli引理，只需证对∀ε＞0，有

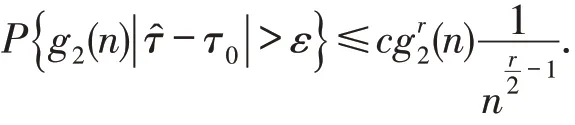
若取g2(n)=n1-γ-δ2，只要取

综上所述，由Borel-Cantelli引理的应用可得，，即定理3结论成立.

3 结语

本文用CUSUM方法讨论线性过程方差变点值的相合量及其收敛速度.比较定理2和定理3可知，当时，变点估计τ^的强弱收敛速度相同，当时，变点估计τ^的强弱收敛速度相差一个慢变函数.进一步还可以讨论{Yi}为弱相关和强相关条件下的方差变点估计的相合性和收敛速度.