于“再创造”过程中提升数学抽象素养
吴厚仪



【摘 要】数学抽象素养作为数学学科核心素养之一,其形成和发展具有连续性和阶段性,贯穿学生数学学习的始终。如何从初中阶段开始逐步发展学生的数学抽象素养,使学生逐渐学会运用数学抽象思维去发现、分析和解决问题,为高中阶段数学学习奠定基础,这是一个值得深思的问题。本文以一节“全等三角形”习题课的教学设计为例,探讨探讨如何在初中几何课堂教学中更好地发展学生的数学抽象素养。
【关键词】初中数学;平面几何;数学抽象素养
数学是客观现象抽象概括而逐渐形成的科学语言与工具,抽象性是数学的本质属性之一。因而,《义务教育数学课程标准(2011年版)》中明确规定,义务教育阶段的数学课堂要培养学生的抽象思维。同样地,最新颁布的《普通高中数学课程标准(2017版)》提出,要发展学生的数学学科核心素养,其中就包括数学抽象。数学抽象是指通过对数量关系与空间形式的抽象,得到数学研究对象的素养。主要包括:从数量与数量关系、图形与图形关系中抽象出数学概念及概念之间的关系,从事物的具体背景中抽象出一般规律和结构,并用数学语言予以表征。
由此可见,数学抽象素养的形成和发展具有连续性和阶段性,贯穿其数学学习过程的始终。数学抽象素养是适应学生终身发展和社会发展需要的与数学有关的关键能力和思维品质之一,能使学生养成在日常生活和实践中运用数学抽象的思维方式思考并解决问题,学会把握事物的本质,以简驭繁。本文从一节“全等三角形”习题课出发,探讨如何在初中几何课堂教学中更好地发展学生的数学抽象素养。
一、经历“再创造”过程,提升数学抽象素养
《义务教育数学课程标准(2011 年版)》提倡反映数学知识应用的过程应该是“问题情境—建立模型—求解验证”的过程。本课例中,笔者将从“提出问题—归纳猜想—证明猜想—得出结论—应用模型—推广延伸”六个环节开展数学活动。
(一)提出问题
例1:如图1,∠A=∠B=∠DEC =60°,求证:∠1=∠C,∠D=∠2。
变式1:如图2, AB⊥BC,AB⊥AD,DE⊥EC,求证:∠1=∠C,∠D=∠2。
(二)归纳猜想
思考1:观察图1和图2,它们有什么共同点?从中你能发现什么规律?
猜想1:如图3,在△ADE和△BEC中,如果∠A=∠B=∠DEC ,那么∠1=∠C,∠D=∠2。
(三)证明猜想
证明猜想1(学生独立完成证明)
(四)得出结论
结论:如图3,在△ADE和△BEC中,如果∠A=∠B=∠DEC ,那么∠1=∠C,∠D=∠2。
师:你能给这一新发现的几何模型取名吗?给大家半分钟进行小组讨论,为模型取个好名字。
生:这两个三角形连在一起像两座山峰,不如就叫“双峰模型”吧!
师:非常形象的名字!大家喜欢这个名字吗?好的,那么我们就给这一模型取名为“双峰模型”。
【设计意图】在“提出问题—归纳猜想—证明猜想—得出结论”的数学活动过程中,教师首先通过对比例1及变式1,引导学生观察、发现、分析和归纳图形的特征,从中归纳并形成简单的数学猜想,然后帮助学生对所得猜想进行严格证明,最后得出结论。在数学活动中提高合情推理和演绎推理的能力的同时,学生逐步学会清晰地用数学语言归纳概括自己的想法;在尝试数学抽象的初步过程有深刻体会的同时,学生逐渐学会从特殊到一般、从具体到抽象的思维方式,在潜移默化中不断提升数学抽象素养。另外,让学生给所发现证明的几何模型命名,学生能从数学学习中获得极大的成就感,提高学生数学学习的自我效能感,激发学生学习数学的积极性。
(五)应用模型
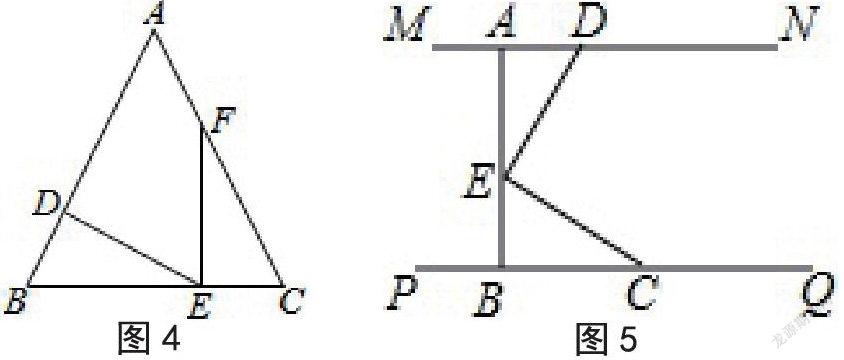
练习1:如图4,在△ABC中,∠B=∠C,点D、E、F分别在AB、BC、AC上,且BD=CE,∠DEF=∠B,图中是否存在和△BDE全等的三角形?说明理由。
练习2:如图5,MN∥PQ,AB⊥MN,∠DEA=∠ECB,求证:DE⊥EC.
(六)推广延伸
思考2:如果把猜想1的条件和结论互换,你能得到怎样的命题?
猜想2:如图3,如果∠1=∠C,∠D=∠2 ,那么∠A=∠B=∠DEC.
证明猜想2(学生独立完成证明)
应用模型2
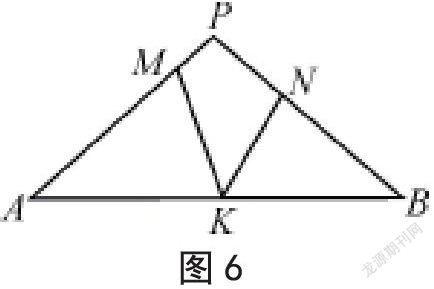
练习:如图6,在△PAB中,PA=PB,M,N,K分别是PA,PB,AB上的点,且AM=BK, BN=AK,若∠MKN=44°,则∠P的度数为?
思考3:如果把图3的△ADE和△BCE沿直线AB分别向左右两边平移一定距离,如图4所示,此时结论是否依旧成立?
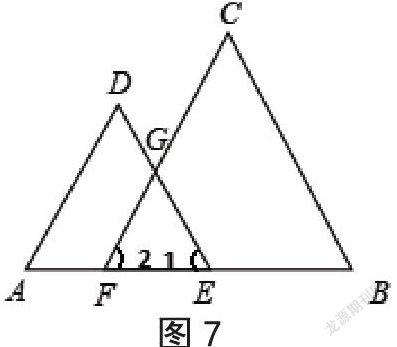
猜想3:如图7,在△ADE和△BCF中,∠A=∠B=∠EGF.求證:∠1=∠C,∠2=∠D.
证明猜想3(学生独立完成证明)
应用模型3
练习:如图8,∠A=∠ABC=90°,CE=BD,过点C作CF⊥BD,垂足为点F,延长CF交AB于E.试证明:BE=AD。
【设计意图】首先,通过将猜想1的条件和结论互换,得出猜想2这一逆命题并证明,不仅是对“双峰模型”再建和完善的过程,更是对学生数学抽象素养形成的巩固过程。然后,在学生能从图3直接抽象出数学命题并证明其正确性的基础上,通过对图3进行平移变换得到更复杂的关联图形图4,引导学生从关联图形中抽象出数学命题并证明,将已知数学命题推广延伸至更一般的情形,这不仅是对“双峰模型”拓展和丰富的过程,更是对学生数学抽象素养形成的深化过程。总而言之,在“推广延伸”环节中,学生再度经历“提出问题—归纳猜想—证明猜想—得出结论”的活动过程,加深了学生对数学知识生成的体会,有助于数学抽象素养的培养和提升。
二、总结
(一)精心设计变式,激活学生数学抽象思维
在初中数学几何课程中,相关平面图形往往有多种位置与形状,图形变化的复杂性、多样性和抽象性大大增加了学生学习几何的难度。因此在几何内容教学中采取变式教学显得尤为重要。高质量的变式设计是在初中数学几何课堂中进一步完善几何知识体系建构、培养学生数学抽象素养的基础和保证。教师要从图形的特征和数学命题的内容出发,充分体现“观察—思考—猜想—证明—应用”这一数学知识的再创造、理解和应用过程,展现图形的变换过程和命题证明的思考过程。这一过程的展现可以通过教师在贯彻螺旋上升原则和化隐为显原则的前提下,变换问题中的条件或结论,精心设计一系列由浅入深、环环相扣的变式,不断地给学生提供比较、分析、归纳、综合的机会,启发引导学生在不同的几何问题情境中抽象概括出几何对象的内在联系特征,将具体的几何对象和内容进行归类和“浓缩”,通过反复的体验实践,保持学生积极有效的思维活动,深化学生对几何知识的认识和理解,使学生养成运用数学抽象思维方式解决问题的习惯,学生的抽象思维能力在递进问题的探索中得到了发展。
(二)展开“再创造”过程,引导学生主动进行数学抽象
著名教育家苏霍姆林斯基曾说:“在人的心灵深处,都有一种根深蒂固的需要,就是希望自己是一个探索者、发现者、研究者,而在儿童的精神世界中,这种需要特别强烈。”正如学生发现“双峰模型”时内心颇具成就感一样,在数学学习的过程中,发现是一种乐趣,通过“再创造”过程展现习题的精彩,能够激发学生主动去发现去探究,享受探究学习的乐趣。而且,学生对通过自身抽象思维活动自主获得的知识比由旁人“填鸭式”硬塞的知识理解得更透彻,掌握得更迅速。因此,在几何课堂中,教师要努力营造轻松、愉悦的探究学习氛围,充分发挥学生的主观能动性,激起学生强烈的求知欲和表达欲,让学生主动经历数学知识的再创造过程,搞清楚知识的来龙去脉。在这一过程中,学生能够亲身体验过去的数学家们从特殊到一般的数学抽象思维过程,对数学的抽象本质和通过数学抽象形成数学知识的过程有更深刻的理解,促进学生数学抽象素养的形成和发展。
(三)把握抽象程度,教学设计符合学生认知规律
初中生的认知发展正处于具体运算阶段向形式运算阶段过渡的关键期,这时学生的数学认知结构中的抽象思维、逆向思维等开始发展,并能进行简单的演绎推理。因此,初中几何教学要符合初中生的认知规律,把握一个适当的“度”,本着严密性和量力性原则,以适合初中生的接受能力为宜,不应为了发展学生的数学抽象素养而过多研究复杂图形问题。
数学抽象是数学的基本思想,是形成理性思维的重要基础,反映了数学的本质特征,贯穿在数学产生、发展、应用的过程中。数学抽象使得数学成为高度概括、表达准确、结论一般、有序多级的系统。数学抽象的重要性地位可见一斑。教师要充分挖掘教学资源,在初中数学几何课堂上让学生经历探索知识的过程,产生数学思考的欲望,在实践中体验知识形成的过程和内在联系,体会获得知识的喜悦,在提高学生推理论证能力的同时,不断潜移默化地提升学生的数学抽象素养,真正学会用数学抽象思维去发现、分析和解决问题。
【参考文献】
[1]毛锡荣,钱军先.“教师稚化思维,促进学生理解”的理论研究与实践探索[M].苏州大学出版社,2018.
[2]章建跃.数学核心素养如何落实在课堂[J].中小学数学,2016(3).
[3]岳峻,罗建宇.例谈数学核心素养如何落实在课堂[J].中学数学,2017(7).
(責任编辑:周玮凌)

