基于类比思想的解题研究

刘玲玲

摘要：类比思想方法是一种数学思想方法，可以帮助学生形成良好的解决数学问题的思维习惯，并锻炼学生举一反三的思维，对于初中数学教学质量的提升有着事半功倍的作用. 本文根据类比思想的特点探讨图形旋转中的类比这种类型，主要目的在于通过研究类比探究题的相关内容，阐述类比思想在数学解题中的应用.

关键词：类比思想;中学数学;解题教学

一、类比思想的内涵

类比最早的起源地在希腊，大意是通过观察猜想事物之間一些特征的相似度然后极大限度地推演为事物的相似. 心理学是最早开始探索有关类比思想奥秘的学科，且大量研究表明类比思想已经有较多而且比较成熟的研究成果.美国著名心理学家桑代克（Edward Lee Thorndike）提出：任何事物都有其独有的特点，学生在不清楚某一事物的特性时，应从基础抓起，了解事物的基本特质，顺藤摸瓜找到其本质，从而触类旁通、举一反三地解决其他有着类似特质的问题. 在数学发展史上，其中受类比思想的影响最大的是美籍匈牙利数学家波利亚（Geoeg Polya），在他的三本著作《怎样解题》、《数学的发现》、《数学与猜想》中，大量地提到了类比推理[1]. 之后，波利亚又提出了合情推理的概念，所谓合情推理，是由已经存在且正确的基本事实或根据个人数学直觉而进行的一种大胆推测猜想.类比是根据两个（或两类）不同的对象之间在某些方面或相似之处猜测他们在其他方面也有可能有相同或相似，并做出某种判断的推理方法[2].

二、类比思想在中学数学教学中的应用价值

（一）培养学生解题意识和探究精神

诚如数学家欧拉所言：“类比是伟大的引路人. ”在剖析数学问题时，充分地利用“类比”思想去探究分析问题本质，排除思维障碍，会大大提高学生解决问题的能力和效率. 教学实践证明，从类比思想的角度审视数学问题并以此渗透到解题实践，对培养学生的解题意识和探究精神，使学生从中真正感受数学应用的广泛性都是十分必要的.

（二）加强各个数学知识点之间的联系

事实上，学生是否能够扎实地掌握各个知识点，并且能够将其串联到起，对于学生是否能够尽快形成数学思维，强化学生的学习效率有很大的影响. 类比思想，赋予了教师更丰富的教学手段，也给予了学生更厂阔的联想空间，可以推动学生自主地学习很多新的知识、方法，寻求出与众不同的解题思路，探索数学内在规律[3].

三、图形旋转中的类比解题研究

在初中的数学中，图形的变换被广泛使用，主要有：对称、平移、旋转与位似，在初中几何题型中常出现的是图形旋转. 旋转作为一种基本的图形变换方法，让学生通过它的动态过程，感悟、猜想、验证几何图形所具有性质的“变”与“不变”[4]. 在教学过程中，这类题目的关键之处在于掌握特殊到一般的研究方法，由特殊图形的性质和特点逐步探究出一般题型的性质. 类比探究题是考试中的十分重要的新题型，其样式多变、考察范围广、覆盖知识面广，这类题型应引起教师足够的重视.

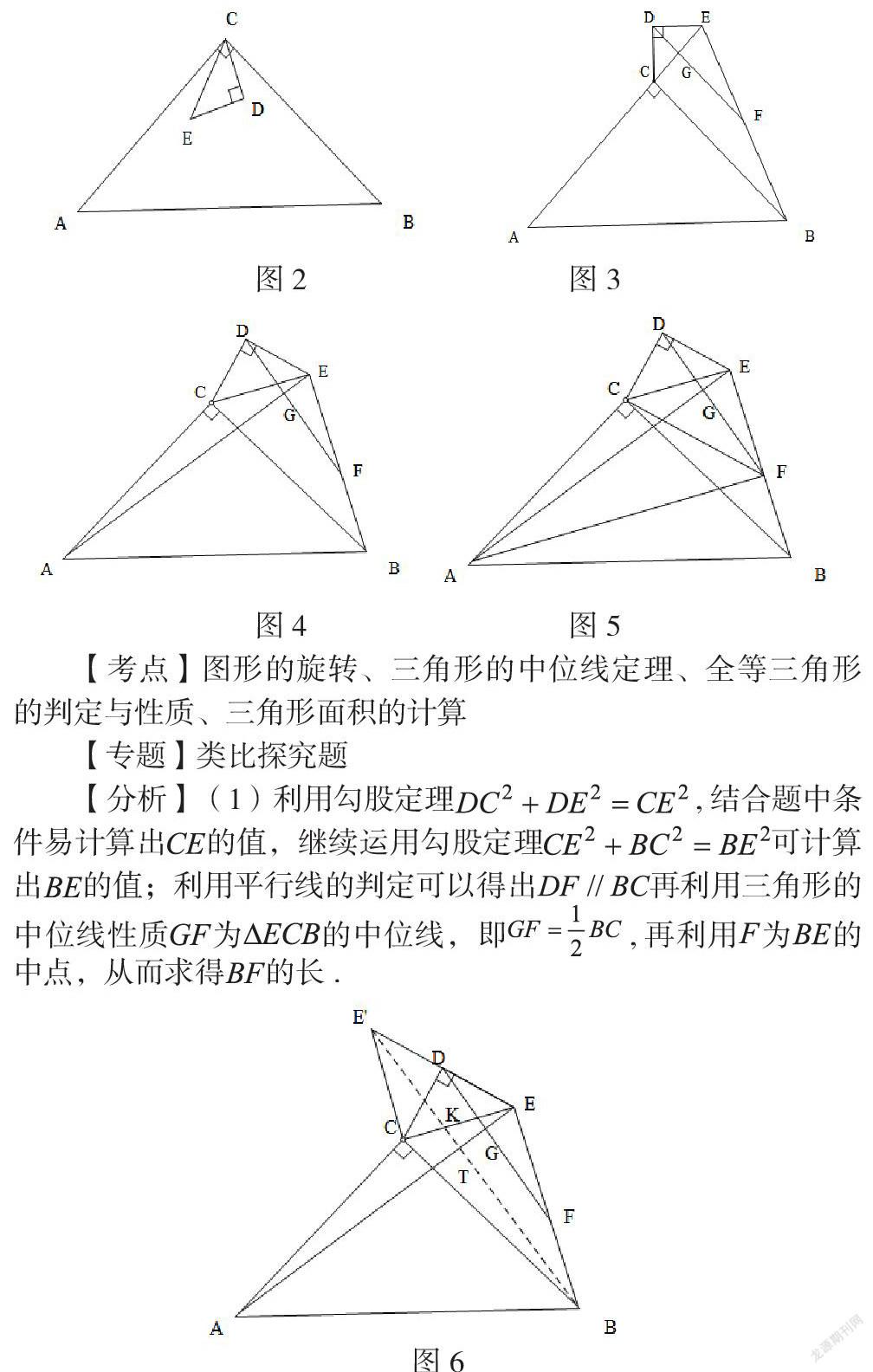
例3. 1如图2，△ABC与△EDC为等腰直角三角形，AC=BC=12，DE=DC=4，，将绕着点旋转.

（1）初步尝试，如图3，在旋转过程中，当A，C，E三点共线（E在AC延长线上）时，连接BE，过D点作AE的垂线交于点G，交BE于点F，则的长为 .

（2）探究证明，如图4，在旋转过程中，连接AE，BE，过D点作AE的垂线交AE于点G，交BE于点F，猜想EF与BF的数量关系并证明.

（3）探究拓展，如图5，在（2）的条件下，连接CF，AF，当AF最小时，请直接写出△ACF的面积.

【考点】图形的旋转、三角形的中位线定理、全等三角形的判定与性质、三角形面积的计算

【专题】类比探究题

【分析】（1）利用勾股定理，结合题中条件易计算出的值，继续运用勾股定理可计算出的值;利用平行线的判定可以得出再利用三角形的中位线性质为的中位线，即，再利用为的中点，从而求得的长.

（2）. 将绕点逆时针旋转得到，连接，，如图6，由旋转性质出发，易先证出全等于，得出，由可得出，由平行线的判定可得出，应用问题（1）的方法即可得出结论，与其不同之处在于第（2）问仅仅是将进行了旋转变化，证明了三角形全等后得到其对应角相等，这是第一问的升华以及深层次的挖掘. 第（2）问的证明过程充分运用了类比思想方法，清晰展现了类比思想在解题中的优势.

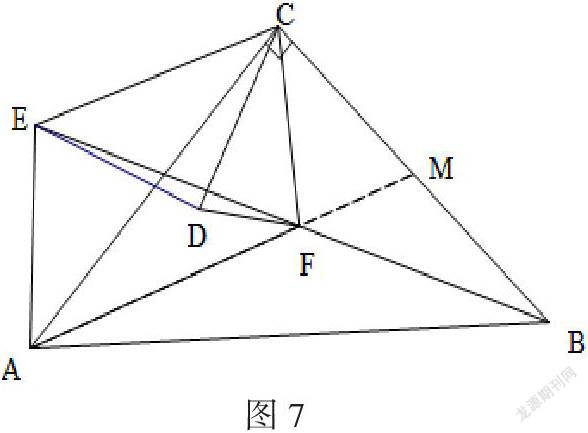
取的中点，连接，，如图7，要使最小，只有当点在线段上，根据三角形中位线定理可求得的长，进而利用三角形面积的比例关系求得，从而得出.

【点评】这道以三角形旋转为背景的类比探究题涉及知识点有三角形中位线性质，平行线的判定，三角形全等判定，三角形旋转的性质等等.这道题的解决过程极大地考查了类比在解题的应用以及学生的逻辑推理能力. 学生首先需要作出定性分析、判断、甚至猜想，明确解题方向，再进行更加具体的分析、论证. 运用类比，可以让学生在比较中发现解题规律与方法，并能运用这种方法来解决新的问题，有利于强化学生的解题能力. 类比法是学生发现解题思路的重要手段，甚至是发现新知识、新规律的重要手段.

由上述探索可见，充分运用类比思想猜想、分析、判断、论证数学问题是解决数学问题的一个重要且关键的思想方法，具有十分现实和长远的意义. 事实上，要在解题研究中进行创新必然要把数学思想方法的教学置于一个重要的地位.

参考文献：

[1]罗钦. 高中数学教学中类比思想的应用[D].西华师范大学，2019.

[2]孙春阳. 类比思想在数学教学中的渗透[J]. 初中数学教与学，2014（02）：20-22

[3]徐美娟. 类比思想在高中数学教学中的应用研究[D].南京师范大学，2015.

[4]杜洪格. 初中数学类比探究题的实践研究[D].洛阳师范学院，2019.