2020年中考“函数”专题解题分析
姜黄飞 陈世文









摘 要:函数是整个中学阶段的核心知识,贯穿始终,是学习的一条主线,是研究运动变化的重要数学模型,统领着数与式、方程与不等式,也是连接“图形与几何”与“数与代数”的桥梁,是中考考查的重点内容. 综观2020年全国各地区中考试卷中的函数试题,既关注对函数基本概念、图象和性质的考查,又重视函数与“数与代数”“图形与几何”的关联,强调函数与其他知识的内在联系,把抽象的数量关系和直观的图象相结合,突出数与形的结合,动态地分析问题,不仅考查函数的基础知识、基本技能和基本方法,同时考查学生的思维能力、实践能力和创新能力.
关键词:函数模型;数形结合;考查要求;问题解决
一、主要考点分析
函数是“数与代数”领域的重要内容,在“数与代数”部分占有重要的地位,由常量教学过渡到变量教学是数学思维的一大飞跃. 函数的主要考查内容包括:探索简单实例中的数量关系和变化规律;了解常量、变量的意义;了解函数的概念和三种表示方法;能结合图象对简单实际问题中的函数关系进行分析;理解一次函数、反比例函数与二次函数的概念、图象和性质,并利用这三类函数解决简单的实际问题. 同时,函数与方程、不等式,函数与几何图形的结合也是函数部分的重点考查内容.
函数的性质着眼于函数中的数量特征,函数的图象着眼于图形特征,充分体现了利用数与形的结合研究函数的基本方法和思路,在函数的学习过程中应当加以渗透,在复习过程中应当重点关注. 函数是研究运动变化的重要数学模型,蕴涵着丰富的数学思想与方法. 因此,函数也是考查学生分析问题和解决问题能力的有效载体. 综观2020年全国各地区中考试卷中的函数试题,都立足基础知识和基本技能,考查与其他数学知识的联系,凸显数学思想和方法,积累用函数知识解决实际问题的基本活动经验. 下面以2020年全国各地区中考试卷中的部分“函数”试题为例加以分析.
1. 注重基础,考查核心概念和表达式
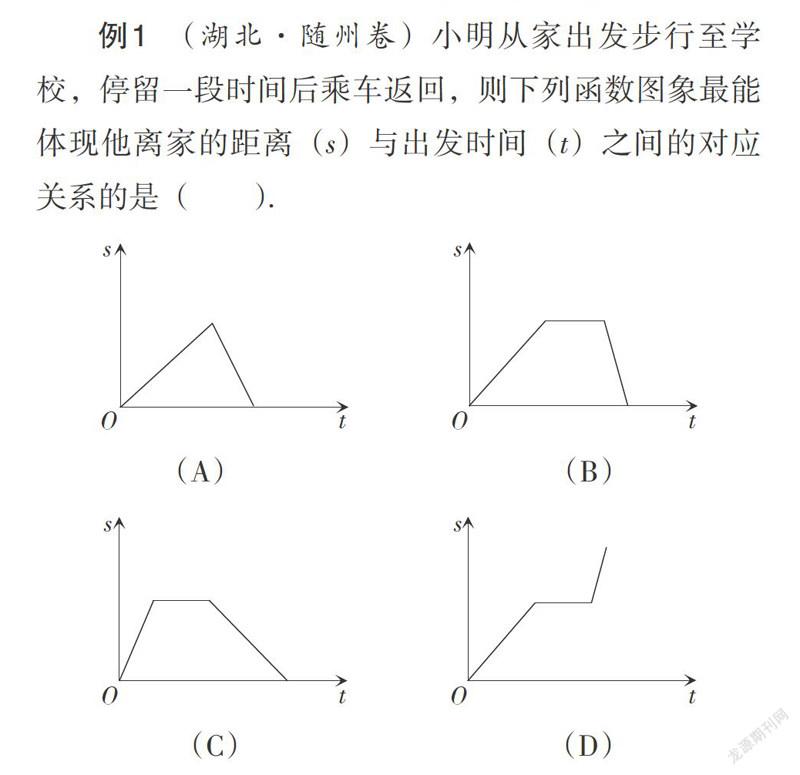
例1 (湖北·随州卷)小明从家出发步行至学校,停留一段时间后乘车返回,则下列函数图象最能体现他离家的距离(s)与出发时间(t)之间的对应关系的是( ).
(A) (B)
(C) (D)
解析:此题选取学生较为熟悉的生活情境考查函数的概念,探究小明离家的距离(s)与出发时间(t)两个变量之间的关系,用图象法来表示函数. 小明从家出发步行至学校时,可以近似看成是一次函数图象,是一條从原点开始的线段,停留一段时间时,离家的距离不变,所以为一条平行于横轴的线段,再乘车返回,离家的距离较快地减小至0,选项B符合题意,故此题选择B.
例2 (贵州·黔西南州卷)如图1,在菱形ABOC中,[AB=2,] [∠A=60°,] 菱形的一个顶点C在反比例函数[y=][kx k≠0]的图象上,则反比例函数的解析式为( ).
(A)[y=-33x] (B)[y=-3x]
(C)[y=-3x] (D)[y=3x]
解析:此题考查了用待定系数法求反比例函数的表达式. 在菱形ABOC中,[∠A=60°,] 菱形边长为2,所以[OC=2,∠COB=60°.] 如图2,过点C作[CD⊥OB]于点D,则[OD=1,CD=3.] 所以点C的坐标为C[-1, 3]. 因为点C在反比例函数[y=kx k≠0]的图象上,得[k=][-3.] 所以反比例函数的解析式为[y=-3x.] 故此题选择B.
【评析】对于函数概念的考查,往往依托一定的生活情境,在实际情境中抽象出数量关系,研究两个变量之间的相互联系,感受函数的本质是一种对应关系,解析法、列表法、图象法是表示函数的三种形式. 在2020年全国各地区中考试题中,对函数的三种表示形式都有相应的考查,是考查的基础,也是核心.
2. 蕴涵思想,考查函数图象与性质
例3 (山东·威海卷)一次函数[y=ax-a]与反比例函数[y=ax a≠0]在同一坐标系中的图象可能是( ).
(A) (B)
(C) (D)
解析:此题考查一次函数[y=kx+b k≠0]和反比例函数[y=kx k≠0]的图象位置与表达式中比例系数k,b之间的关系,考查两类函数的基本性质.
选项A,由函数[y=ax-a]的图象可知[a>0,-a>0,]而由函数[y=ax a≠0]的图象可知[a>0],相矛盾,故选项A错误.
选项B,由函数[y=ax-a]的图象可知[a<0],由函数[y=ax a≠0]的图象可知[a>0],相矛盾,故选项B错误.
选项C,由函数[y=ax-a]的图象可知[a>0],由函数[y=ax a≠0]的图象可知[a<0],相矛盾,故选项C错误.
选项D,由函数[y=ax-a]的图象可知[a<0],由函数[y=ax a≠0]的图象可知[a<0],故正确.
所以此题选择D.
例4 (福建卷)已知[P1x1,y1,P2x2,y2]是抛物线[y=ax2-2ax]上的点,下列命题正确的是( ).
(A) 若[x1-1>x2-1,] 则[y1>y2]
(B) 若[x1-1>x2-1,] 则[y1<y2]
(C) 若[x1-1=x2-1,] 则[y1=y2]
(D) 若[y1=y2],则[x1=x2]
解析:此题考查二次函数的对称轴和增减性,因为抛物线[y=ax2-2ax=ax-12-a,] 所以抛物线的对称轴为[x=1].
由于a的符号不确定,故要分类讨论.
当[a>0]时,图象开口向上,在对称轴[x=1]的左边y随x的增大而减小,而在对称轴的右边y随x的增大而增大,若[x1-1>x2-1,] 则[y1>y2] ,故选项B错误.
当[a<0]时,若[x1-1>x2-1,] 则[y1<y2],故选项A错误;若[y1=y2],则[x1-1=x2-1,] 故选项D错误.
所以此题选择C.
此题若借助图象数形结合,也可直观地求解.
【评析】对函数性质的考查,主要涉及解析式中的系数变化与函数图象位置的关系、函数的增减性、对称性和最值,都体现了数与形的完美结合. 由此可见,理清函数性质与系数的关系是解决此类问题的基本保障,数形结合思想是解决此类问题的基本思想.
3. 联系生活,考查函数应用和建模能力
例5 (湖北·天门、仙桃、潜江、江汉油田卷)小华端午节从家里出发,沿笔直道路匀速步行去妈妈经营的商店帮忙,妈妈同时骑三轮车从商店出发,沿相同路线匀速回家装载货物,然后按原路原速返回商店,小华到达商店比妈妈返回商店早5分钟,在此过程中,设妈妈从商店出发开始所用时间为t(分钟),图3表示两人之间的距离s(米)与时间t(分钟)的函数关系的图象;图4中线段AB表示小华和商店的距离[y1] (米)与时间t(分钟)的函数关系的图象的一部分. 试根据所给信息解答下列问题.
(1)填空:妈妈骑车的速度是________米 / 分钟,妈妈在家装载货物所用时间是________分钟,点M的坐标是________;
(2)直接写出妈妈和商店的距离[y2] (米)与时间t(分钟)的函数关系式,并在图4中画出其函数图象;
(3)求t为何值时,两人相距360米?
解析:此题考查在实际情境下,学生对一次函数的读题、识图能力,需要学生具备一定的逻辑推理、数学建模、直观想象和数学运算能力.《义务教育数学课程标准(2011年版)》(以下简称《标准》)要求要能用数学的思维方式观察、分析现实世界中的现象,解决在日常生活和其他学科学习中遇到的问题,增强应用数学的意识和能力.
第(1)小题,由图4可得小华的速度为[1 80030=][60](米 / 分钟),由图3可知第10分钟时小华和妈妈在途中相遇,所以两者的速度之和为[1 80010=180](米 / 分钟). 所以妈妈骑车的速度为120米 / 分钟,是小华速度的2倍. 又因为妈妈骑车从商店出发到家往返路程也是小华的2倍,所以若不装载货物时则应该同时达到. 所以小华到达商店比妈妈返回商店早的5分钟即为妈妈在家装载货物,时间为5分钟. 而妈妈从商店出发到家需要[1 800120=15] (分钟),所以点M的横坐标为20. 此时s为小华走的路程[20×60=1 200] (米),所以点M的坐标为[M20,1 200]. 此题以填空的形式给出,要解答正确需要对整个过程有清晰的认识,这是正确解答下面问题的前提.
有第(1)小题做铺垫,第(2)小题难度不大. 可以先画出函数图象,如图5,当[0≤t<15]时,对应图象为OC段,[y2=120 t;] 当[15≤t<20]时对应图象为CD段,[y2=1 800;] [20≤t≤35]时对应图象为DE段,利用待定系数法,设[y2=kt+b,] 将点[D20,1 800]和 [E35,0]分别代入,解得[y2=-120 t+4 200.] 所以[y2=][120 t 0≤t<15,1 800 15≤t<20,-120 t+4 200 20≤t≤35.]
第(3)小題需要分段讨论.
① 相遇前,依题意有[60 t+120 t+360=1 800,] 解得[t=8];
② 相遇后,依题意有[60 t+120 t-360=1 800,] 解得[t=12];
③ 依题意,当[t=20]时,妈妈从家里出发开始追赶小华,此时小华距商店为[1 800-20×60=600](米),只需10分钟,即[t=30]时,小华到达商店. 而此时妈妈距离商店为[1 800-10×120=600](米)>360(米),所以[120t-5+360=1 800×2.] 解得[t=32.]
故t为[8,] 12或32分钟时,两人相距360米.
此题也可以结合图5,直观的发现分三段借助解析式求解.
【评析】此题从实际情境出发,以一次函数为载体,较好地考查了学生将实际问题转化为数学问题的抽象能力和建模思想. 在第(1)小题中,需要由逻辑推理得到“妈妈在家装载货物的时间为5分钟”,其实也可以通过妈妈往返的速度相同,结合小华比妈妈早到5分钟确定出妈妈返回的图象为DE段,通过先画出妈妈和商店的距离[y2] (米)与时间t(分钟)的函数图象,再通过数形结合轻松破解问题. 第(3)小题可以从“数”的角度分段求解,也可以从“形”的角度借助直观想象解决问题. 如图5,数形结合,通过函数解析式求解. 在2020年全国各地区中考试题中,如黑龙江鹤岗卷第25题、黑龙江牡丹江卷25题、江苏淮安卷第24题、浙江宁波卷第22题、浙江衢州卷第22题、宁夏卷第24题等都对此有相关考查.
4. 知识关联,考查函数与方程不等式
例6 (贵州·遵义卷)如图6,直线[y=kx+b](k,b是常数[k≠0])与直线[y=2]交于点[A4,2,] 则关于x的不等式[kx+b<2]的解集为 ________ .
解析:此题考查函数与不等式的关系,借助图象,运用数形结合是解决此类问题的关键. 直线[y=][kx+b](k,b是常数,[k≠0])与直线[y=2]交于点[A4,2,] 所以当[x<4]时,[y<2.] 所以关于x的不等式[kx+b<2]的解集为[x<4.]
例7 (河北卷)如图7,现要在抛物线[y=x4-x]上找点[Pa,b],针对b的不同取值,所找点P的个数,三人的说法如下. 甲:若[b=5,] 则点P的个数为0;乙:若[b=4,] 则点P的个数为1;丙:若[b=3,] 则点P的个数为1. 下列判断正确的是( ).
(A)乙错,丙对 (B)甲和乙都错
(C)乙对,丙错 (D)甲错,丙对
解析:此题考查了函数与方程的关系,可以从“数”的角度,将点[Pa,b]代入抛物线[y=x4-x,] 得[4a-a2=b.] 甲:若[b=5]时,[4a-a2=5],方程无解,对应点P的个数为0;乙:若[b=4]时,[4a-a2=4,]方程有两个相等实数根,对应点P的个数为1;丙:若[b=3]时,[4a-a2=3],方程有两个不相等的实数根,对应点P的个数为2,故选项C正确.
此题也可以从“形”的角度出发,由抛物线[y=x4-x]得顶点为[2,4],则如图8所示,借助几何直观即可得解.
【评析】例6中,求不等式[kx+b<2]的解集,只知直线过点[A4,2],是不能确定直线解析式的. 但是借助一次函数的图象,只需找到[y<2],即直线在点A下方对应的横坐标范围即可. 例7找满足条件的点的个数,等价于对应方程解的个数问题,借助数形结合,直观想象,使问题得解. 综观2020年全国各地区中考试题,对函数与方程、函数与不等式的考查非常广泛,用函数的视角解决方程和不等式问题,是考查的一个核心.
二、典型解法评析
1. 关注最值问题考查,强化性质应用
二次函数最值问题的考查是中考的热点,它也是二次函数的一个重要的性质,往往将一般式转换为顶点式,或是直接应用顶点公式求最值. 值得注意的是,中考中许多涉及二次函数的试题,往往含字母系数,或是自变量的取值在一定范围内,求函数最值时通常需要分类讨论,结合函数的基本性质来确定函数的最值.
例8 (湖北·孝感卷)在平面直角坐标系中,已知抛物线[y=ax2+4ax+4a-6 a>0]与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,顶点为点D.
(1)当[a=6]时,直接写出点A,B,C,D的坐标:
A ,B ,C ,D ;
(2)如图9,直线DC交x轴于点E,若[tan∠AED=][43],求a的值和CE的长;
(3)如图10,在(2)的条件下,若点N为OC的中点,动点P在第三象限的抛物线上,过点P作x轴的垂线,垂足为点Q,交AN于点F;过点F作[FH⊥DE,] 垂足为点H. 设点P的横坐标为t,记[f =FP+FH.]
① 用含 t 的代数式表示 f;
② 设[-5<t≤m m<0,] 求[f]的最大值.
解:(1)当[a=6]时,抛物线的表达式为[y=6x2+][24x+18.] 令[y=0],则[x=-1]或[x=-3.] 当[x=0]时,[y=18.] 函数的对称轴为[x=-2],所以点A,B,C,D的坐标分别为[A-3,0, B-1,0, C0,18, D-2,-6.]
(2)因為[y=ax2+4ax+4a-6,]
所以点[C0,4a-6.]
因为函数的对称轴为直线[x=-2],
所以点D的坐标为[-2,-6.]
由点C,D的坐标易求得直线CD的表达式为[y=2ax+][4a-6.]
所以点[E3a-2,0.]
所以[tan∠AED=OCOE=6-4a3a-2=43.]
解得[a=23].
所以点C,E的坐标分别为[C0,-103, E52,0.]
所以[CE=OC2+OE2=256.]
(3)① 如图11,作ED与FP的延长线交于点J,由(2)知抛物线的表达式为[y=23x2+83x-103.]
所以点A[-5,0],点[C0,-103.]
所以点[N0,-53.]
所以可求得直线AN的表达式为[y=-13x-53.]
设点[Pt, 23t2+83t-103],则点[Ft,-13t-53.]
所以[PF=-23t2-3t+53].
又由点E,C易得直线CE的表达式为[y=][43x-103,]
所以点[Jt, 43t-103].
所以[FJ=-53t+53.]
因为[FH⊥DE,] [JF∥Oy],
所以[∠FHJ=∠EOC=90°,∠FJH=∠ECO.]
所以[△FJH∽△ECO.]
所以[FHEO=FJEC.]
所以[FH=-t+1.]
则[f=PF+FH=][-23t2-4t+83.]
② 因为[f =-23t2-4t+83=-23t+32+263]([-5<t≤][m],且[m<0]).
所以当[-5<m<-3]时,[fmax=-23m2-4m+83];
当[-3≤m<0]时,[fmax=263.]
【评析】此题在求解最值之前,考查了用待定系数法求函数表达式、函数图象与坐标轴的交点坐标、二次函数求顶点坐标、对称轴等基础知识,以及用含字母的式子表示线段长,利用相似三角形求线段长等知识. 用含字母的式子来表示线段长对学生而言有一定的难度,这些往往是最后借助二次函数求解最值问题的准备. 而第(3)小题第②问中自变量[-5<t≤m,] 且[m<0],m的值又不确定,需要对m的值进行分类讨论. 因为[f=-23t+32+263]图象的开口向下,在对称轴的左边y随x的增大而增大,在对称轴的右边y随x的增大而减小,顶点时函数取到最大值,所以当[-5<m<-3]时,在对称轴的左边,当[t=m]时,f取到最大值,当[-3≤m<0]时,包含顶点,所以最大值为[263]. 此题比较全面地考查了对二次函数相关知识的应用,尤其是第(3)小题第②问的最值更是需要学生对增减性和最值有较好地理解,强化了对性质运用的考查.
2. 关注系数考查,强化数形结合
对函数表达式中各项系数的符号问题的考查,尤其是对二次函数中各项系数的符号和数与形之间相互关联的考查是历年中考的热点问题,也是2020年全国各地区中考中的热点问题. 例如,湖北随州卷第10题、广东东莞卷第10题、广东深圳卷第11题、贵州遵义卷第12题、黑龙江牡丹江卷第20题、湖南常德卷第7题等对此都有所考查. 此类问题需要学生对二次函数表达式中的系数a,b,c和判别式的符号与图象的开口方向、对称轴的位置、图象与坐标轴的位置关系等有明确的认识,以及对已知点对应满足的代数式進行化简运算的能力.
例9 (广东·深圳卷)二次函数[y=ax2+bx+][c a≠0]的顶点坐标为[-1,n],其部分图象如图12所示. 以下结论错误的是( ).
(A)[abc>0]
(B)[4ac-b2<0]
(C)[3a+c>0]
(D)关于x的方程[ax2+bx+c=n+1]无实数根
解:因为抛物线开口向下,所以[a<0]. 由对称轴为[x=-b2a=-1.] 得[b=2a<0.] 又因为抛物线与y轴交于y轴正半轴,所以[c>0.] 所以[abc>0.] 所以选项A正确.
因为抛物线与x轴有两个交点,所以[b2-4ac>0],即[4ac-b2<0]. 所以选项B正确.
因为抛物线的对称轴为[x=-1],抛物线与x轴的一个交点在[-3,0]和[-2,0]之间,所以抛物线与x轴的另一个交点在[0,0]和[1,0]之间. 当[x=1]时,[y<0.] 所以[a+b+c<0.] 把[b=2a]代入,得[3a+c<0.] 所以选项C错误.
因为抛物线开口向下,顶点为[-1,n],所以函数有最大值n. 所以抛物线[y=ax2+bx+c]与直线[y=n+1]无交点,对应一元二次方程[ax2+bx+c=n+1]无实数根. 所以选项D正确.
故此题选择C.
【评析】此题为对二次函数图象与系数关系的典型考查,系数a的符号决定图象的开口方向,当[a<0]时,抛物线开口向下;当[a>0]时,抛物线开口向上. 而b的符号取决于a的符号和对称轴的位置,对称轴在y轴的左侧,则a,b同号;对称轴在y轴的右侧,则a,b异号. 常数c是抛物线与y轴交点的纵坐标. 解决此类问题一般都需要判断a,b,c的符号,在此题中即是选项A所考查的;由图象与x轴的交点情况,确定判别式的符号,即选项B所考查的;而对于选项C的考查则需要在试题中寻找一个不等式和一个等式结合判断,这里选择“当[x=1]时,得[a+b+c<0]”和“由对称轴[x=-1],得[b=2a]”,结合求解,这也是解决只含a,b,c中的两个字母的不等式的解题策略;对于选项D则只需关注函数的最值,借助数形结合,直观想象可解.
3. 关注面积问题的考查,巧用联想转化
例10 (重庆A卷)如图13,在平面直角坐标系中,矩形ABCD的对角线AC的中点与坐标原点重合,点E是x轴上一点,连接AE. 若AD平分[∠OAE,] 反比例函数[y=kx k>0,x>0]的图象经过AE上的两点A,F,且[AF=EF],[△ABE]的面积为18,则k的值为( ).
(A)6 (B)12
(C)18 (D)24
解:如图14,连接BD,OF,过点A作[AN⊥OE]于点N,过点F作[FM⊥OE]于点M.
因为[AN∥FM,AF=FE,]
所以[MN=ME,FM=12AN.]
因为点A,F在反比例函数的图象上,
所以[S△AON=S△FOM=k2.]
所以[ON=12]OM.
所以[ON=MN=EM.]
所以[ME=13OE.]
所以[S△FME=][13S△FOE.]
因为AD平分[∠OAE,]
所以[∠OAD=][∠EAD.]
因为四边形ABCD是矩形,
所以[OA=OD.]
所以[∠OAD=∠ODA=∠DAE.]
所以[AE∥BD.]
所以[S△AOE=S△ABE=18.]
又因为[AF=EF,]
所以[S△EOF=12S△A0E=9.]
所以[S△FME=13S△FOE=3.]
所以[S△FOM=S△EOF-S△FME=9-3=6=][k2.]
所以[k=12].
故此题选择B.
【评析】此题是反比例函数与三角形知识相结合的综合题,涉及反比例函数系数k的几何意义、平行线的判定、角平分线、等腰三角形的性质、三角形的面积等核心知识,利用平行线进行等积转化,是解决此类问题的基本策略. 此题通过角平分线结合等腰三角形的性质得到[AE∥BD],从而实现[S△ABE]与[S△A0E]的等积转化,进而联想k的几何意义,结合给定的比例关系求解.
此题也可以利用[AF=EF,] 得点A的纵坐标是点F纵坐标的2倍. 不妨设点[Aa,2b],则点F的坐标为[2a,b],从而得点E坐标为[3a,0.] 所以[S△ABE=S△ADE][12 ⋅ 3a ⋅ 2b=18.] 所以[ab=6.] 所以[k=2ab=12.] 按比例关系设点的坐标也是解决此类问题的有效途径.
4. 关注存在性问题考查,强化分类讨论
综观2020年全国各地区中考函数试题,发现存在性问题是一类常见试题,主要考查特殊三角形、平行四边形、特殊平行四边形、相似三角形的存在性问题,或是满足线段或角或面积的特殊数量关系的动点存在性问题等. 此类问题通常考查学生的识图作图、直观想象、逻辑推理、数学运算等关键能力和核心素养,蕴涵函数与方程、数形结合、分类讨论等数学思想方法,涵盖的知识面广,综合性强,考查学生思维的严谨性. 对于学生容易出现漏解的情况,常以压轴题的形式呈现. 例如,浙江湖州卷第24题、广西玉林卷第26题、贵州黔东南州卷第26题、黑龙江大兴安岭卷第24题、湖北黄冈卷第25题、湖南郴州卷第26题、湖南常德卷第25题都考查了平行四边形存在性問题;重庆A卷第25题考查了菱形存在性问题;黑龙江牡丹江卷第28题考查正了方形存在性问题;浙江衢州卷第23题考查了直角三角形存在性问题;贵州遵义卷第24题考查了等边三角形存在性问题;湖北随州卷第24题、广东东莞卷第25题、湖北鄂州卷第24题等考查了相似三角形存在性问题;山东淄博卷第24题考查了一定面积关系存在性问题等.
例11 (贵州·黔东南州卷)如图15,已知抛物线[y=ax2+][bx+c a≠0]与x轴交于A,B两点(点A在点B的左边),与y轴交于点[C0,-3],顶点D的坐标为[D1,-4].
(1)求抛物线的解析式;
(2)在y轴上找一点E,使得[△EAC]为等腰三角形,试直接写出点E的坐标;
(3)点P是x轴上的动点,点Q是抛物线上的动点,是否存在点P,Q,使得以点P,Q,B,D为顶点,BD为一边的四边形是平行四边形?若存在,试求出点P,Q坐标;若不存在,试说明理由.
解:(1)因为抛物线的顶点坐标为[D1,-4,]
设抛物线的解析式为[y=ax-12-4,]
将点[C0,-3]代入抛物线,得[a=1.]
所以抛物线的解析式为[y=x2-2x-3.]
(2)由抛物线的解析式[y=x2-2x-3]得点B,A的坐标分别为[B3,0,A-1,0.]
所以[AC=10.]
设点[E0,m],则[AE=m2+1],[CE=m+3.]
因为[△ACE]是等腰三角形,分三种情况讨论.
① 当[AC=AE]时,[10=m2+1],
解得[m=3]或[m=-3](舍).
所以点[E0,3.]
② 当[AC=CE]时,[10=m+3],
解得[m=-3±10.]
所以点[E0,-3+10]或[0,-3-10.]
③ 当[AE=CE]时,[m2+1=m+3],
解得[m=-43.]
所以点[E0,-43.]
综上所述,点E的坐标为[0,3, 0,-3+10][0,-3-10],[0,-43];
(3)存在. 理由如下.
如图16,因为顶点D的坐标为[D1,-4],将线段BD向上平移4个单位长度,再向右(或向左)平移适当的距离,使点B的对应点落在抛物线上,这样便可以找到存在的点Q,此时点D的对应点就是点P. 所以点Q的纵坐标为4,
设点[Qt,4],将点Q的坐标代入抛物线[y=x2-][2x-3],得[t2-2t-3=4.]
解得[t=1+22]或[t=1-22].
所以点[Q11+22,4]或[Q21-22,4.]
分别过点[D,Q1]作 x 轴的垂线,垂足分别为点F,G.
因为抛物线[y=x2-2x-3]与x轴的右交点B的坐标为[B3,0],且[D1,-4.]
所以[FB=PG=3-1=2.]
所以点P的横坐标为[1+22-2=-1+22]或[1-22-2=-1-22.]
综上所述,点[P1-1+22,0],点[Q11+22,4]或点[P2-1-22,0],点[Q21-22,4.]
【评析】此题是一道二次函数的综合题. 第(1)小题考查了二次函数的顶点式,用待定系数法求函数的表达式. 第(2)小题则考查了等腰三角形的存在性问题,以AC为一边在 y 轴上找一点E,使得[△EAC]为等腰三角形,通过设点E的坐标,表示出[△EAC]的三条边长,将边两两相等进行分类讨论. 此题也可以对以AC为底或以AC为腰进行分类讨论,属于较为常规的存在性问题. 第(3)小题考查平行四边形的存在性问题,明确以BD为一边时的存在性问题. 笔者选用了平移BD的方法,找到平移后的位置,再进行推理运算. 此题也可以从平行四边形顶点坐标特点出发求解,因为点P,B都在x轴上,所以点Q和点D的纵坐标的绝对值相等,先锁定点Q的纵坐标,再确定点P的坐标. 此题第(2)(3)小题分别考查了等腰三角形和平行四边形的存在性问题,用好分类讨论,抓住平行四边形四个顶点坐标之间的关系,是解决此类问题的有效途径.
三、试题解法赏析
例12 (浙江·宁波卷)如图17,经过原点O的直线与反比例函数[y=ax a>0]的图象交于A,D两点(点A在第一象限),点B,C,E在反比例函数[y=]
[bx b<0]的图象上,[AB∥Oy],[AE∥CD∥Ox],五边形ABCDE的面积为56,四边形ABCD的面积为32,则[a-b]的值为 ________,[ba]的值为 ________ .
解:(方法1)如图18,连接AC,OB,OC,OE,
由题意得点A,D关于原点对称.
所以点A,D的纵坐标的绝对值相等.
又因为[AE∥CD,]
所以点E,C纵坐标的绝对值相等.
又因为点E,C在反比例函数[y=bx]的图象上,
所以点E,C关于原点对称.
所以点E,O,C三点共线.
因为[OE=OC,OA=OD,]
所以四边形ACDE是平行四边形.
由题意,得[a-b=a+b=2S△AOE=S△ADE=24.]
又因为[S△AOC=S△AOE=S△AOB,]
所以点B,C到AD的距离相等.
所以[AD∥BC.]
所以[S△AOB=S△DOC=12.]
所以[S△BOC=8.]
所以[BCOD=S△BOCS△COD=812=23.]
延长CB交 x 轴于点F,设AB交[x]轴于点G,
则有[△BGF∽△AGO.]
所以[BGAG=BFAO=BFDO=13.]
所以[ba=BGAG=13.]
所以[ba=-13].
(方法2)同方法1,得[a-b=24,AD∥BC.]
如图19,延长AB,DC交于点H,
则[△BCH∽△ADH.]
所以[BCAD=BHAH.]
因为[S△ACB=32-24=8,]
所以[S△ADC∶S△ABC=24∶8=1∶3.]
所以[BC∶AD=1∶3.]
所以[HB∶HA=1∶3.]
设[BH=k,] 则[AH=3k,AG=HG=32k.]
所以[BG=12k.]
所以[BG∶AG=1∶3.]
所以[ba=BGAG=13.]
所以[ba=-13].
(方法3)同方法1,得[a-b=24,AD∥BC.]
如圖19,设[S△BCH=s.]
则[HBBA=HCCD.]
所以[S△BHCS△ABC=S△ACHS△ADC.]
所以[s8=8+s24.]
解得[s=4.]
所以[S△ADH=S△ADC+S△ABC+S△BCH=24+8+4=36.]
所以[S△AOG=14S△ADH=14×36=9.]
所以[a=18,] [b=-6.]
所以[ba=-13.]
【评析】此题主要考查反比例函数比例系数的几何意义和平行线间的等面积转化. 如图18,反比例函数[y=ax a>0]中对a的几何意义的理解为[a=2S△AOP],反比例函数[y= bx b<0]中,[-b=b=2S△EOP],所以[a-b]就是[△AOP]和[△EOP]面积和的2倍,即[△AOE]面积的2倍. 再利用反比例函数图象中点的对称性,得[S△AOE=][S△DEO.] 所以[a-b]就是[△ADE]的面积. 图中[S△AOE=S△DOC=][S△AOB=12a-b],[S△AED=S△ACD=S△ABD=a-b.] 求[ab]的值,关键在于[AD∥BC]的发现,以上解法中通过对称性得[S△AOE=S△AOC.] 通过几何意义,得[S△AOE=S△AOB.] 从而得[S△AOC=S△AOB.] 得[AD∥BC.] 此题还可借助[S△ACD=S△ABD,] 得[AD∥BC.] 进而借助两直线平行,利用相似或面积进行比例的转化,这也是求解反比例函数问题常用的转化方法.
总之,综观2020年全国各地区中考试题中对函数内容的考查,既关注对函数核心概念与性质等基础知识和基本技能的考查,又重视函数与“数与代数”“图形与几何”的关联,强调函数与其他知识的融合;关注数形结合、分类讨论等基本数学思想的运用和基本活动经验的积累;关注对学生思维能力、实践能力和创新能力的考查,充分发挥了试题的导向作用. 引导数学教师认真研究《标准》,研究试题考查的方向、类型和方式,总结解题策略,重视学生的思维形成过程,在解题教学中培养学生理性思考的能力,落实数学学科核心素养.
参考文献:
[1]中华人民共和国教育部制定. 义务教育数学课程标准(2011年版)[M]. 北京:北京师范大学出版社,2012.
[2]张伟,宋先波,赵洁. 2018年中考“函数”专题解题分析[J]. 中国数学教育(初中版),2019(1 / 2):54-63.
[3]胡玲君. 2019年中考“函数”专题解题分析[J]. 中国数学教育(初中版),2020(1 / 2):63-71.

