“互联网+信息技术”数学解题教学交互式课件应用探索

赵智勇 刘瑞锋

摘要：“互联网+信息技术”的发展，推动了教学模式全方位的转变。传统教学模式中所使用的教学方法和策略，教育学习资源等，都无法满足新型的教学模式。因此，课题组对基于“互联网+信息技术”的新型教学模式下的教学方法和策略、教育学习资源等多方面开展必要的探索研究。解题教学是初中数学教学中培养学生解题能力的重要部分，本文基于“互联网+信息技术”的数学解题教学实践，以交互式课件资源的制作和应用为例，从交互式课件的优势、数学问题串设计、信息技术关键突破三个方面进行浅要的分析。

关键词：互联网+信息技术;解题教学;交互式课件

“互联网+信息技术”的发展，推动了教学模式全方位的转变。新型教学模式下师生之间的连接依托于各式各样的电子产品终端。与传统教学模式相比，学生与教师的互动变得更为困难，无法向课堂一样面对面的沟通，层层递进地引导，也无法满足由于反应能力不同和思路不同导致的的学生个性化需求。但新型教学模式具有不受空间和时间限制，教学安排灵活，授课方式多样等优点。并且基于“互联网+信息技术”的课堂得益于信息技术的应用，有利于教学难点的突破，激发学生的学习兴趣等。

解题教学是培养学生解题能力的重要部分，是数学教学活动的重要形式。我们要提高新型教学模式下数学解题教学的教学效果，就要开展基于“互联网+信息技术”的教学模式下的教学方法和策略、教育学习资源等多方面的教学实践与探索。

根据“互联网+信息技术”的数学课堂的特点和初中解题教学的过程需求，再结合课题组的教学探索与实践，我们认为若要弥补新型教学模式的先天不足，可以充分发挥交互式课件的优势，以“数学问题串”设计为实现交互与引导的手段，把信息技术做为对问题关键难点进行突破的工具，设计适合基于“互联网+信息技术”的数学解题教学的交互式课件服务于教学，使“互联网+信息技术”与新型教学模式谐畅融合，可以有效提高解题教学的教学效果。

1 交互式课件的优势——实现学生个性化学习需求

传统课堂教学中，教学课件的设计主要是将教学内容、关键词句等展示给学生。而面對不同能力的学生，开展针对学生个性化需求的教学安排，主要依靠师生之间面对面的互动来实现。

在基于“互联网+信息技术”的新型教学模式下，课件需要智能判断并满足学生的个性化学习需求。随着信息技术的发展，课件的“交互”功能逐渐被广大教师广泛应用到教学中去，我们将具备交互功能的课件称为“交互式课件”。交互式课件的优势就是可以智能判断并实现学生的个性化学习需求。

交互式课件的交互原理：

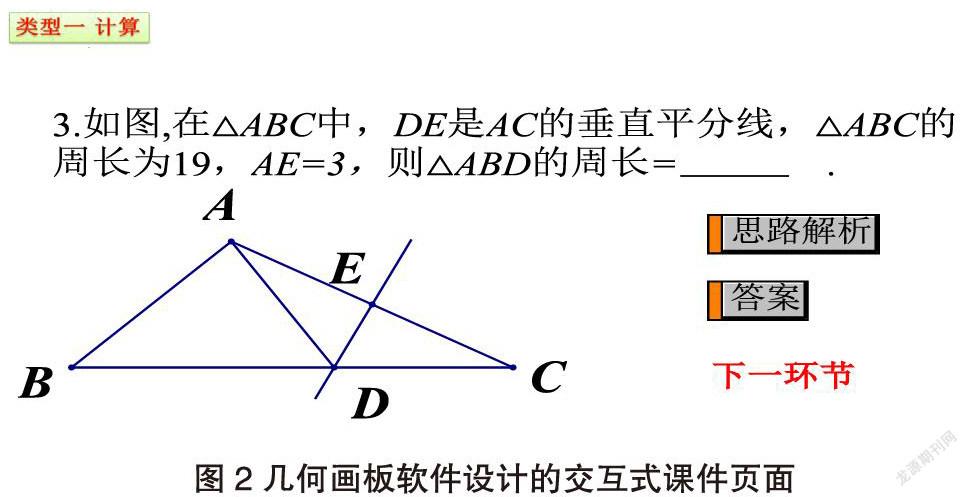
实现智能判断的方法可以是软件的交互式按钮或选框，也可以是课件模块之间的链接等等。下面以常用的几何画板软件设计的交互式课件页面作为示例：

本课件设计思路：

教师在使用本课件进行解题教学时，考虑到学生的能力不同，有的需要对关键条件进行分析，有的还需要对解题思路进行引导，对于个别能力强的同学需要核对答案后再进行个性化学习。

因此，课件中，题目的所有条件均采用了热字设计，学生在使用课件时只要鼠标点击对应条件，或移动到对应条件上，就可以看到对应的条件解析。课件下方还有思路解析和答案的按钮，满足学生的个性化需求。

课题组在实践中发现，在制作交互式课件时还要注意几方面内容：

（1）通过可控性满足交互情景的多样化。课件可以根据需要灵活控制，呈现所需要展示的情形，让学生自己去探索，亲自参与知识的生成。

（2）要满足交互的个性化。不同的学生对题目的解决遇到的困难不尽相同，也可能会选择不同的解题思路，交互式课件可以给予不同学生不同的选择。

（3）课件设计的模块要互联互通。不论是一条线还是多条线;不论是目录式还是树状图式，模块之间要互联互通，并且模块的设置要尽量全面。

2 “数学问题串”设计——交互式课件实现交互与引导的手段

苏格拉底曾经说过“知识的传授和学习的本质是通过多个提问使其对已有知识的恢复记忆”。因此，设计数学问题串时要注意针对特定的数学问题，根据学生已有的认知基础，围绕核心概念和思想方法，提出多个具有引导性的问题，帮助学生解决问题，达成教学目标。

以“数学问题串”设计做为手段，设计交互式课件进行数学解题教学，既可以培养学生的审题能力，帮助学生理清思路，还可以通过层层引导，激发学生的学习兴趣，改变学生的学习方式，培养学生的创新意识。

例1：柏拉图的《美诺篇》中记载了一个故事：一个朋友向苏格拉底求教如何将“把一个正方形面积加倍”？

苏格拉底并没有直接告诉他答案，而是通过层层引导，使这位朋友的奴隶在每个正方形上画一条对角线，由四条对角线作为四边的图形是正方形，其面积正是原来正方形的2倍。

由以上故事可以知道，用两个边长相同的正方形可以制作成一个大正方形.

①若两个相同正方形的边长为a，则制作成的大正方形边长为多少？

②已知用三个边长为a的正方形可以制作成一个大正方形，则该大正方形的边长为多少？

③请结合图文说明三个边长相同的正方形可以制作成一个大的正方形.

这道解答题共有三小问，问题本身就已经是问题串的形式。①帮助学生回忆了已经解决的问题，学生再结合勾股定理，很快会得出答案为a。②也较易在第一个问题的经验上结合勾股定理得出答案为a。问题③有一定难度，如果学生无法完成，就需要我们通过“数学问题串”的形式来引导学生解决问题。

问题一：如果大正方形的边长应为a，我们应该如何得到这样长度的边来作为大正方形的边呢？

问题设计意图：引导学生利用勾股定理进行探索，得出边AM长为a的直角三角形ABM。

问题二：这样的边还能找到另一条么？

问题设计意图：引导学生利用勾股定理进行探索，得出边NG长为a的直角三角形GHN。

问题三：这两条边所在的三角形是否可以通过变换，构成大正方形的某一部分？

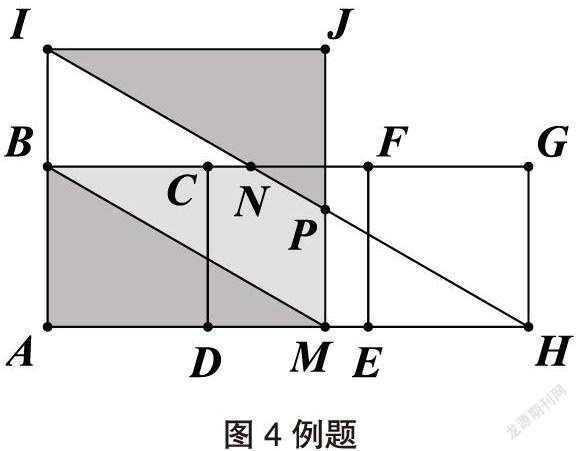
问题设计意图：引导学生利用平移变换进行探索，得到大正方形的基本框架（阴影部分），这个过程可能是尝试了多次错误的变换，但是带有目的的尝试会逐步纠正错误的结果，直到问题的解决。

问题四：大正方形AMJI框架外面的部分（三角形PMH）与框架内空白部分（三角形IBN）全等么？

问题设计意图：引导学生对结论进行计算验证，并理清解题思路。

问题五：你在解决这个问题的时候用到了哪些数学方法和思想？是什么条件让你想到了这些方法？这些方法和思想还能在类似的题目中使用么？

问题设计意图：引导学生及时反思，积累数学活动经验，促成数学解题思维的跃进。

本题的解题思路不仅仅这一种，在制作交互式课件时，可以依据学生对前一个问题的回答，设置不同的下一问题。

信息技术——交互式课件问题关键难点的突破工具

2011版义务教育数学课程标準指出：“数学课程的设计与实施应根据实际情况合理地运用现代信息技术，要注意信息技术与课程内容的整合，注重实效。要充分考虑信息技术对数学学习内容和方式的影响，开发并向学生提供丰富的学习资源，把现代信息技术作为学生学习数学和解决问题的有力工具，有效地改进教与学的方式”。

交互式课件的一个基本功能即是课件的可操作性，利用信息技术制作可操作性的交互式课件开展解题教学，既可以让学生动手操作，积累基本活动经验，又可以改变知识的呈现方式，从而突破问题的关键难点。

例2：如图，点A为x轴上任意一点，点B（0，2），以AB为边做出等腰直角三角形ABC，当点A在x轴上移动时，点C与原点O之间的最小距离为（）

交互式课件设计意图：在这个几何画板课件中，学生通过拖动点A的位置，可以发现点C的轨迹是一条直线（可以使用软件功能记录点C的轨迹），再根据点到直线最短距离不难解决问题。

可以实现课件设计意图的软件有很多，作为一名数学教师，将信息技术与自己教学的谐畅融合，才能使课堂更加高效，更易取得优异的成绩。

提升学生解题教学能力的方法还有很多，我们要抓住每一个教学关键环节，提高教学活动的质量，发挥新型教学方式的优势，争取使学生获得更好更全面的发展，包括学生的辩证唯物主义世界观、刻苦专研精神、坚强意志和独立工作等优良品质以及数学各方面的核心素养。

参考文献：

[1]代钦.数学教学论新编[M].北京：科学出版社，2018.

[2]G.波利亚，徐泓，冯承天译.怎样解题[M].上海：上海科技教育出版社，2011.

[3]郤云江.移动互联网下的教学工具[M].杭州：浙江教育出版社，2017.

基金项目：本文系河南省教育科学规划2020年度一般课题《基于“互联网+信息技术”的初中数学解题教学实践研究》研究成果.课题批准号：2020YB0980。

赵智勇1 刘瑞锋2

1 河南省安阳市教育局教研室

2 河南省安阳市曙光学校