重力式码头抗滑稳定性公式中的逻辑思维课堂探索

曾春华　张会领　吴光林

摘  要：本文以提炼重力式码头抗滑稳定性公式逻辑思维为教学案例，论述了公式中蕴含的质量度、整体与局部、主次与递进的逻辑关系。提升了港口水工建筑物课堂学习的深度、拓展了学习目标的维度、构建了港口航道与海岸工程专业知识和逻辑思维的系统性。

关键词：重力式码头;抗滑稳定性;逻辑思维;港口水工建筑物

中图分类号：U656.1    文献标识码：A    文章编号：1673-7164（2021）19-0094-07

港口水工建筑物是港口航道与海岸工程专业的一门专业教育核心课程，课程以工程水文学、土力学、材料力学、结构力学、钢筋混凝土结构、港口规划与布置、港口装卸工艺等课程为基础。通过该课程的学习，学生应熟悉港口水工建筑物各类结构形式及特点、一般构造;理解作用在水工建筑物上的荷载及荷载组合，掌握基本计算内容及设计状况，运用现行国家及行业规范标准进行港口水工建筑物计算和设计;进一步拓展对港口水工建筑物的经济性、安全性、使用要求和施工条件等方面思考，增强学生对学科和专业的兴趣，培养学生的专业素养。为学生顺利从事港口航道与海岸工程及其相关领域的专业技术工作奠定基础[1-3]。

由于港口水工建筑物是港口航道与海岸工程专业的一门综合性课程，是串联本专业众多课程的知识绳索。课程中存在大量“体型巨大”的公式，所以学习难度相对较大。部分同学甚至存在以将来不从事本专业工作为理由，认为没必要花大力气去学习此课程知识的误区。若授课教师过于注重知识点的讲解而忽略思维体系的归纳提炼，单纯聚焦于设计原理和方法，会使学习枯燥，导致学生对大公式及其囊括的诸多知识点产生混乱，甚至出现害怕和排斥大公式的现象。

重力式码头在多种教材中均是介绍的第一种码头结构，对整个课程及后续其他码头结构的学习具有典型示范的作用。本文结合多年的工程实践和教学实践，以重力码头抗滑稳定公式为例，对港口水工建筑物课程的授课和港航专业人才培养逻辑思维方面进行了一些探索和研究。

一、重力式码头抗滑稳定验算课程内容

（一）重力式码头的主要特征

重力式码头是我国分布较广、使用较多的一种码头结构形式。其结构坚固耐久，抗冻和抗冰性能好;能承受较大的地面荷载和船舶荷载，对较大的集中荷载以及码头地面超载和装卸工艺变化适应性较强，维修费用少，是港务部门和施工单位比较欢迎的码头结构形式。按墙身结构来看，重力式码头可分为方块码头、沉箱码头、扶壁码头、大圆筒码头、格型钢板桩码头、干地施工的现浇混凝土和浆砌石码头等。随着施工工艺的提升及施工船机的大型化，沉箱码头成为现阶段我国最常用的一种结构形式。沉箱结构重力式码头结构复杂，主体结构一般由抛石基床、沉箱及箱内回填砂、胸墙、后方抛石棱体和回填土等多个部位组成，承受的作用复杂（包括波浪、潮沙、海流、冰凌、风、地震等自然力和使用、施工荷载），施工条件多变，建设周期长，投资较大[4]。

（二）设计工况

根据JTS167-2018《码头结构设计规范》，岸壁码头应开展沿墙底面、墙身各水平缝和基床底面的抗滑稳定性验算。主要包括以下几种工况[5]：

（1）考虑波浪作用，堆载土压力为主导可变作用。

（2）考慮波浪作用，波浪力为主导可变作用。

（3）不考虑波浪作用，且由可变作用产生的土压力为主导可变作用。

（4）不考虑波浪作用，沿胸墙底面的抗滑稳定性验算，系缆力为主导可变作用。

具体工程会在此基础上演化出更详细的设计工况。

本文选取工况（1）为代表展开论述抗滑公式中蕴含的逻辑体系，并以此拓展理解其他工况乃至港口水工建筑物课程教材中其他公式。

（三）抗滑稳定计算公式

根据JTS167-2018《码头结构设计规范》和港口水工建筑物课程教材[4]，工况（1）抗滑稳定计算公式如式（1）所示：

γ0（γEEH+γPWPW+γEEqH+γψPPB）≤■（γGG+γEEV+γEEqv+γψUPBU）f  （1）

式中γ0——结构重要性系数;

γE——土压力分项系数;

EH、EV——计算面以上永久作用总主动土压力的水平分力标准值和竖向分力标准值（kN）;

γPW——剩余水压力分项系数;

PW——作用在计算面以上的剩余水压力的标准值（kN）;

EqH、Eqv——计算面以上可变作用总主动土压力的水平分力标准值和竖向分力标准值（kN）;

ψ——作用组合系数，持久组合取0.7，短暂组合取1.0;

γd——结构调整系数，无波浪作用或波浪为非主导可变作用时取1.0， 有波浪作用并为主导可变作用时取1.1;

γG——自重力的分项系数，取1.0;

G——作用在计算面以上的结构自重力标准值（kN）;

f——沿计算面的摩擦系数设计值;

γp——波浪水平力分项系数;

PB——波谷作用时计算面以上水平波浪力的标准值;

γU——波浪浮托力分项系数;

PBU——波谷作用时计算底面上时的波浪付托力的标准值（kN）。

二、质、量、度逻辑关系

质量度的概念在黑格尔《逻辑学》“有论”“本质论”和“概念论”三编中的“有论”编内系统展开。黑格尔以对立统一思想阐明了关于质量互变精彩的辩证思想。黑格尔整个逻辑学的概念层次中第一层次是质、量、度[6-7]。

首先是质，具体概念是按照从抽象到具体，从简单到复杂的途径自我发展的。质是直接的、抽象的、简单的规定性。重力式码头抗滑公式（1）本质上是简洁的F≤Nf，即滑动力要小于等于垂直力乘以摩擦系数，这是中学的物理知识。在重力式码头抗滑稳定计算中，即滑动合力设计值要小于等于结构垂直方向合力设计值乘以沿计算面的摩擦系数设计值。透过“繁杂而冗长”的计算公式，提炼出最简洁的公式，有利于学生以最快速度抓住抗滑公式的本质，还可以激发学生追求事物本质表述的美感，犹如爱因斯坦的质能公式“E=mc2”激发学生对科学之美的赞叹，简洁的抗滑公式同样可以激发同学们对工程之美的向往和学习积极性。

其次是量，从质进展到量表示人类认识的一种深化和具体化，是完成的质的存在。量是比较具体和复杂的规定性。抗滑公式分拆到结构自重G、永久主动土压力E、剩余水压力PW、堆货荷载产生的可变主动土压力Eq以及波谷压力PB产生的作用力标准值，体现了从“一到多”质过渡到量的过程，需要融入前置课程知识进行定量计算。反之，量的变化若超过了量的一定界限，会导致公式性质发生转变，抗滑稳定逆转为不稳定，从量转化为质的过程。

最后是度，质所依赖的限量就是度。黑格尔给度下的定义是“度是有质的限量”。度既非单纯的质， 也非单纯的量，而是二者的统一。黑格尔认为从质发展到量是人类认识的一种深化，但还需从量的片面认识进一步“提高到量的规定的普遍形式，以至成为一个规律或说一个尺度的环节”，体现了从量过渡到度的必要性和必然性。重力式码头抗滑公式中，各作用力分项系数γ，就是度的具体体现及符号表示，是为保证所设计的码头结构具有规定的可靠度而在设计表达式中采用的系数，是通过大量工程实例的统计及系统性验证试验而确定的，在确保港口水工建筑物安全性的同时兼顾经济性。这些度的系数不是凭空得出，是大量具体工程实例和试验的统计和抽象得出的[8]，是质的反映。要在大量具体数据中，分析研究并确定各参数的取值范围，实现量的具体化，需要根据港口工程结构的安全等级来确定结构重要性系数γ0，根据结构的受力特点确定结构调整系数γd，达到根据作用力的影响效应重要性及码头的安全等级进行度的把控，最终实现质和量的统一。值得注意的是，体现分项系数的值不能过大，不然超出所体现作用力应有的体现，还会造成工程建设的浪费。值不能过小，否则可能导致结构失稳，发生滑动破坏，引发事故。在一定条件下可以转换，根据《码头结构设计规范》（JTS167-2018）第3.6条款，当永久作用效应对结构承载能力起有利作用时，该作用分项系数取值不应大于1.0。起不利作用时，分项系数取值不应小于1.2[5]。体现了黑格尔认为一切事物皆有度，若过了度就使事物变质。一切事物都是质与量的统一、都有其确定的度的思想。

通过质、量、度的逻辑关系分析，学生可以具体而深刻地认识码头结构稳定性本质与现象的公式化表征。有助于理解、掌握质量度互变的辩证规律。

三、整体与局部逻辑关系

公式（1）的整体与局部逻辑关系结构如图1所示。

整体上，需要根据整体结构安全等级来确定结构重要性系数γ0，根据破坏效果的等级，从很严重到不严重分为三个等级，对总滑动力大小进行1.1、1.0和0.9的放大缩小。还需要波浪为是否为主导可变作用来对整个结构的抗滑力进行调整，如果波浪为是主导可变作用，则结构调整系数γ0为1.1，否则为1.0，公式（1）中，波浪为是非主导可变作用时，结构调整系数γ0为1.0。整体抗滑稳定是根本目标，居于主导地位，统率着各局部作用力，所有局部作用服从和服务于整体抗滑稳定。

局部上，分布单独结构自重G、永久主动土压力E、剩余水压力PW、堆货荷载产生的可变主动土压力Eq以及波谷压力PB产生的作用力标准值，再通过线性组合计算各局部作用力的合力。当局部作用力以无序的结构形成整体时，整体滑动力和抗滑力将无法进行界定，也就无从实现整体功能。

通过整体与局部逻辑关系的分析，可以清晰地对整体进行把控，根据破坏效果和结构对作用的响应进行总体调控，通过结构重要性系数γ0和结构调整系数γd对总滑动力和总抗滑力进行放大缩小来实现。整体是由局部构成的，离开了部分，整体就不复存在;局部是整体中的局部，离开了整体就会丧失其准确定位和含义。局部作用力的功能及其变化甚至对整体的功能起决定作用。整体局部的辩证关系要求树立整体观念和全局的思想，从整体出发，在整体上根据各局部作用力的特点和大小选择最佳结构方案，使整体抗滑功能得到最大限度发挥，实现其安全性、使用要求、经济性和施工条件等综合最优目标。

四、主次与递进逻辑关系

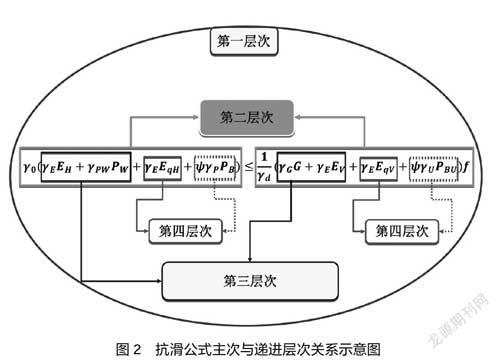
在公式（1）中，整体结构重要性系数γd和结构调整系数γ0在前，其他局部作用力及其分项系数在后，体现了整体为主，局部为次的逻辑关系;在诸多局部作用力中，存在等级划分，非主导可变作用力需要作用组合系数ψ进行调整，持久組合取0.7，短暂组合取1.0。形成四重层层递进的主次关系（图2）。

第一层次。整个公式的根本目的是确定堆货荷载为主导作用、波浪荷载为非主导作用下结构的抗滑稳定性，即确保总滑动力小于总抗滑力。

第二层次。所有局部作用力水平方向分力效应形成的总的滑动合力，所有局部作用力垂直方向分力效应乘以计算面的滑动系数形成总的抗滑合力。两者之间既有共同荷载产生的不同方向的分力，如永久主动土压力E、堆货荷载产生的可变主动土压力Eq和波浪力;又有独立不同的作用力，如剩余水压力PW、结构自重G。

第三层次。永久主动土压力E、剩余水压力PW和结构自重G，当结构方案确定并建设完成后，永久作用将确定下来，不随外部荷载变化而发生变化。

第四层次。可变作用将分为主导可变和非主导可变，以作用效应大者为主导，并且非主导作用需要根据乘以小于等于1.0的组合系数。当然，主导和非主导作用在不同情况下，大小发生变化时，相应的地位也将发生变化。

另一方面，诸多作用力中，永久主动土压力E、剩余水压力PW、结构自重G排在最前面，堆货荷载产生的主导可变主动土压力Eq随后，排在最后的是非主导可变波谷压力PB。由此可见，各作用力的排序也是先后排列的递进关系。

这是事物影响因素的主次分解，即使看似为并列关系也需要讲求递进，比如永久作用和可变作用都需要讲求顺序，需要首先确定永久作用，然后到可变作用。

五、学生逻辑思想的应用拓展及效果

广东海洋大学港口航道与海岸工程专业的大学生培养体系和培养方案中，港口水工建筑这门课程安排在大三下学期进行。大三学生除了学习任务外，还面临关于人生下一阶段的方向和安排的选择，平时零零散散的因素突然都集中涌现，择业或是继续考研深造？是否从事本行业？个人身体、心理、情感、家庭问题，将来的不确定性等等，在此过程中纷纷扰扰的因素众多，部分学生甚至出现无所适从的现象。

笔者将自己多年的工程实践经历和经验融入课程教学案例中，并十分注重逻辑体系的运用，讲述在工程建设过程的所见所闻以及在处理工程建设过程各种问题中逻辑思维的运用，极大地提高了学生的学习兴趣及对自身问题逻辑思维应用的探索和思考能力。学生十分积极踊跃地与任课老师探讨各方面的问题，笔者会结合本课程公式中蕴含的逻辑思维有针对性地与学生分析、探讨及分享自己的经验及建议。剖析学生在特定目标下（抗滑稳定）的自身因素（永久作用、主导可变作用）、外部因素（主导可变作用及非主导可变作用）……参考此公式的逻辑体系进行困惑分解，辅助学生决策，使学生理性可控地做出适合自己的选择。

公式化逻辑分析可增强学习目的的深度、拓展学习目标的维度、构建学习的目标及效果的系统性;能从不同逻辑层次、不同逻辑角度去“找出问题、分析拆解问题、找到解决问题”的逻辑思维体系，很好地奠定了课程教学基础，实现了即时的学以致用。学生对待课程的态度呈现“需要学——值得学——乐意学”的变化过程，成为港口航道与海岸工程专业的合格毕业生。

令人惊喜的是，部分学生毕业一段时间之后专门发信息向笔者反馈，能将面临的困惑和困难看成个人成长的阶梯而非令人沮丧的拦路虎，明白事物在不同情况下作用效应的不同，取决于我们如何运用这些因素（作用力）去解决人生问题，避免人生整体滑坡（滑动破坏），形成积极面对人生的人生观。

参考文献：

[1] 广东海洋大学. 港口航道与海岸工程专业人才培养方案[Z]. 湛江：广东海洋大学大学，2019.

[2] 广东海洋大学. 港口航道与海岸工程专业《港口水工建筑物》课程教学大纲[Z]. 湛江：广东海洋大学大学，2019.

[3] 吴光林，李芳成，张会领，等. 以行业需求为导向的港航专业实践教学体系优化与創新[J]. 科教导刊，2019（09）：68-70.

[4] 韩理安. 港口水工建筑物[M]. 北京：人民交通出版社，2013：20-57.

[5] 中华人民共和国交通运输部. 码头结构设计规范：JTS167-2018[S]. 北京：人民交通出版社，2018.

[6] 陈依元. 试析黑格尔逻辑学质量度概念运动及其合理思想[J]. 青海师专学报，1988（03）：11-17.

[7] 黑格尔. 逻辑学[M]. 梁志学，译. 北京：人民出版社，2002：164-214.

[8] 中华人民共和国住房和城乡建设部. 建筑结构可靠性设计统一标准：GB 50068-2018[S]. 北京：中国建筑工业出版社，2018.

（责任编辑：汪旦旦）